К вопросу о вычислении радиационного давления на сферических включениях

ВВЕДЕНИЕ. ПОСТАНОВКА ПРОБЛЕМЫ

Пожалуй, максимальное число работ, по расчету радиационного давления на включения посвящено сферическим включениям. Работы [1–6] — лишь некоторые, в которых точно решается задача для жидкой или упругой (в том числе и абсолютно мягкой или твердой) сферы произвольного радиуса. Методы решения этой проблемы носят частный, приспособленный к геометрии задачи и виду падающего (осесимметричного) поля, характер. Так, в работах [1, 2] просто решается краевая задача методом, восходящим к Рэлею. В работах [3– 5] решение представляется в упрощенном по сравнению с [1, 2] виде через коэффициенты возбуждения парциальных сферических волн в представлении ближнего поля рассеяния. Наконец, в работе [6] показано, что рассмотрение дальнего поля рассеяния приводит к тем же выражениям, что и в [3–5].

Ранее в работах [7, 8] были получены выражения, связывающие радиационное давление на сложные включения с произвольной амплитудой рассеяния в произвольном падающем поле. Поэтому представляется полезным сравнить соответствующие частные случаи общих выражений из [7, 8] с выражениями, полученными в работах [1– 6].

Для расчета радиационного давления на включения, согласно идеологии [7, 8], необходимо уметь оценивать амплитуды рассеяния этих частиц, поскольку при оценке сил радиационного давления в идеальной жидкости именно эта характеристика, а не физические свойства включения является существенной. В большинстве публикаций на эту тему полагается, что частицы представляют собой жидкие частицы со свойствами, отличными от окружающей жидкости. Однако рассеянию и на упругих телах посвящено значительное число публикаций. Впервые решение этой проблемы для упругих бесконечного цилиндра и сферы было найдено в работе [9]. Затем в работе [10] было предложено уточнение выражений работы [9] для поля рассеяния на упругой сфере, а далее к этой проблеме возвращались неоднократно многие авторы (см. обзоры литературы в работах [11, 12]), в том числе и в связи с вопросами резонансного рассеяния на упругих телах [11].

Следует отметить, что особенно в случае упругой сферы выражения для поля рассеяния, будучи достаточно громоздкими, представлены в крайне разнообразной нотации с множеством различающихся обозначений и видов решения. Так, в работе [9] решение представлено по аналогии с работой [13] через введение многочисленных углов. Примерно так же поступил автор работы [10]. В работах [11, 12, 14] решение выражено через некие определители. В работах [11, 15] решение дано в квантовомеханической нотации, заключающейся в том, что парциальные коэффициенты в разложении поля рассеяния по сферическим функциям выражены в виде, явно отражающем закон сохранения энергии в парциальных слагаемых представления суммарного поля по сферическим гармоникам [15].

Целью настоящей работы является тестирование общих выражений работ [7, 8] применительно к случаю произвольного сферического включения путем сравнения с уже полученными ранее выражениями на примере жидкой и упругой сфер.

РЕШЕНИЕ ЗАДАЧИ

Запишем известные выражения для падающего и рассеянного полей. Так, выражение для плоской волны единичной амплитуды и нулевой фазы, распространяющейся вдоль положительного направления оси Oz при временном факторе e - ^{i m t} , имеет вид [13]

p, = e k = e k ^{cos 6} = j (2 i + 1) j ( kr ) p (cos 6 ).   (1)

I = 0

Выражение для поля рассеянной волны при падении волны (1) на рассеиватель с центром в начале координат имеет вид [11, 15]:

да

P s = j T (2 I + 1) i l h *( kr ) P l (cos 6 ) = l = 0

= тj( e ^{2 S} - 1)(2 1 + 1) ih. *( kr ) P l (cos 6 ).      (2)

2 l = 0

Здесь

( e ^{2 i S} l - 1) = 2T_t = a ;                 (3)

при фиксированном радиусе сферы. Поскольку в работах [3-6] рассматривается случай фиксированного радиуса сферы a , то далее будем придерживаться именно этого случая.

В наиболее удобном, по мнению автора, виде выражение для коэффициентов T приведено в работе [3]:

T ₍ x ) = - Fj ^{( x} ) ^{- xj} l '^{( x} ) l          F l h l ’( x ) - xh_t ”( x ),

где коэффициенты F :

F ( x ) = ^{1 P} x ₂ ²

2 Px al, Sl, Tt — некоторые функции волнового параметра x = ka ; a — радиус сферы; k = ю I с; с — скорость в жидкости; jl и ht 1 — соответственно сферические функции Бесселя и Ханкеля первого рода; (r, 6, ф) — сферические координаты.

Выражение для амплитуды рассеяния получается из (2) подстановкой асимптотики функции

Ханкеля hl\z) ~ — l”1-1 elz при z ^да и вычленени-z eikr ем множителя — [11]. Имеем окончательно:

r

x , j, '( x , )2( l ² + 1 ) j, ( x 2 )

x 1 ^jl '⁽ x 1 ) - ^j l ⁽ x 1 )   ⁽ l^{2 + l - 2) j}l ⁽ x 2 ) ⁺ x 22 ^j I "( x 2 )

/ ^x 1²j C 0y^{2 c )}H^{( x} 1⁾2 j X^

/ _          x 1 ^jl '( x 1) - ^j I ⁽ x j

- 2( l ² + 1 ) ( j ( x 2 ) - x ₂ j '( x ₂ ) ) "  ( l² +l- 2) j ( x ₂ ) + x 2 ² j "( x 2 ) "

Штрих в (6) означает дифференцирование по ар-

гументу x ; с т = —

с 1 - 2 c ₂ ²

f ( 6 , x )

или

f ( 6 , x )

или

f ( 6 , x )

1 j T ( x )(2 1 + 1) P l (cos 6 ), ik l = o

- j T ( x )(2 I + 1) P l (cos 6 );

ix l = 0

-L j a l ( x )(2 I + 1) P (cos 6 ), 2 ik t0

j a l ( x )(2 1 + 1) P l (cos 6 );

2 ix l = o

1 ”

—У ( e ^{2 S ( x} )

2 ik tT

— f ( e ^{2 i S ( x} )

2 ix tT

- 1)(2 l + 1) P (cos 6 ),

- 1)(2 l + 1) P (cos 6 ).

^с 1 ²

-

^С 22

— коэффициент Пу

ассона материала сферы; с 1 , с ₂ — скорость продольной и поперечной волн в сфере соответственно; р 1 — плотность шара; р, с — акустические параметры среды; x 1 = k 1 a , x ₂ = k ₂ a , k_i = ю I с₁ , i = 1,2. Отметим, что выражение (6) получено независимо в работах [3, 10]. В работе [9] в выражении (6) допущена описка, отмеченная автором работы [10]. Отметим, что выражение (6) сводится к случаю жидкой сферы при стремлении к нулю сдвиговой скорости с ₂ .

В системах без потерь коэффициенты F действительны [11], и в этом случае справедливо равенство [15]

| e ^{2 i 5} l | = 1 + a l | =

F l h l ²( x ) - xh l² '( x ) F_lh_l ¹ ( x ) - xh /'( x )

откуда следует, что функции S l ( x ) являются действительнозначными, т. е.

|e^2iSl | = 1.                                 (7а)

Первые выражения в каждой строке (4) удобны при расчетах для фиксированной частоты, вторые —

Вводя обозначения

A 0( x) = a I (x )(2I +1) = OL al (x )(21 +1) = ix2

=     (e2 5 (x) —1)(21 +1),(8)

запишем (4) окончательно в виде разложения функции f (9) по сферическим функциям:

to f (9, x) = £ Az 0( x)P (cos9).(9)

l = 0

Исходя из (7), (8), легко оценить поведение функций A_l ⁰( x ):

Re ( A_z ⁰( x ) ) = a (2 1 + 1)sin2 5_z ( x ),

2 x

Im ( A_z ⁰( x ) ) = a (2 1 + 1) ( 1 - cos2 5_z ( x ) ) .

Отсюда имеем граничные оценки для действительной и мнимой составляющих зональных коэффициентов разложения амплитуды рассеяния по сферическим функциям

- О (2 1 + 1) <  Re ( A z °( x ) ) < О (2 1 + 1), 2 x 2 x

0 <  Im ( A z °( x ) ) < О (2 1 + 1).

2 x

Далее свяжем с помощью (8) действительные и мнимые составляющие функций A_l ⁰ с соответствующими составляющими функций

I, ( x ) = a_z ( x ) + ib_z ( x ):

_D , о     2 z + 17

Re A_z = a-----b_z ,

x т 21 + 1 Im Az =- a-----az.

x

Сравнивая с гармоническим рядом сходящийся ряд (4) и учитывая свойство P (cos 9 )| <  1 при 9 е [0, п] , получаем завышенную оценку для T l ( x ):

1 1* ( x ) <  ^Ь ’ ¹ '' • (12)

Такая же оценка верна и для ее составляющих:

I a z ^{( x} ) <  Ч72Т7’ b z ^{( x} ) < ^-г,    ^^to .   ^(12а)

I                                                                                                                                                                           I

Из (8) и (12) следует оценка

|Az ⁰( x )| = a 2 - + ¹ 1 ( x )| <  xz -¹, l ^« . (13) Отсюда следуют оценки для составляющих функций A ⁰ ( x ), аналогичные (12а).

Ниже приведены примеры расчета зависимостей a ( x ) и b ( x ) для жидкой сферы для некоторых . Параметры таковы:

c = 1500 м/с, c 1 = 2350 м/с, c ₂ = 0 м/с, p = 1000 кг/м³, p 1 = 1200 кг/м³.

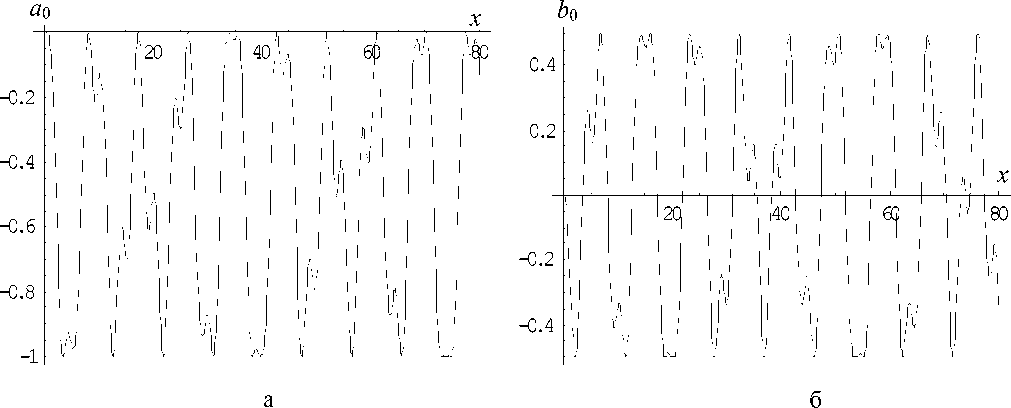
Рис. 1. Зависимости составляющих функции I ( x ) = a _z ( x ) + ib _z ( x ) , I — 0, от x : a ₀ (a), b ₀ (б)

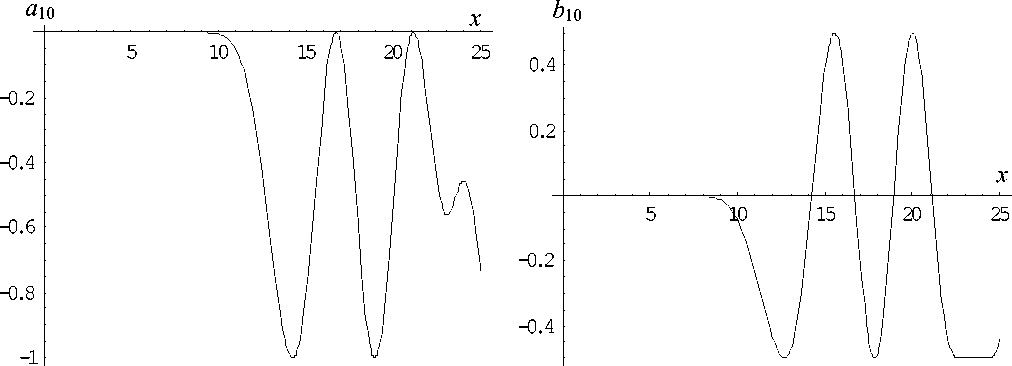
а                                                  б

Рис. 2. Зависимости составляющих функции T₍ ( x ) = a l ( x ) + ib₍ ( x ) , I = 10, от x : a ю (a), b ю (б)

Так, на рис. 1 представлены a ₀( x ) и b ₀( x ), на рис. 2 аналогично представлены a ₁₀( x ) и b ₁₀( x ). Общим в поведении функций является то, что по мере роста номера l , составляющие a_l ( x ) и b_l ( x ) начинают достигать существенных значений при все больших x . Это приводит к необходимости учета все большего количества мультиполей. В целом выполняется приближенное равенство между предельным значением x и необходимым числом учитываемых в расчете радиационного давления мультиполей.

В результате достаточно простых вычислений по методике работы [7] могут быть получены следующие выражения для радиационного давления на радиально-симметричное включение в поле плоской бегущей, стоячей и квазистоячей волн.

Плоская бегущая волна p ₀ e ^ikz . Радиационное давление для z -компоненты равно

F z st — — 2

p lx

2 pc ² 7

x 4 n sin 2 kh 7 a j ( — 1) ^l Re ( A ⁰) + I x l — 0

to

+z l—0

2( l + 1)

4 1 ² + 8 1 + 3

( — 1) ^l Im

p

Здесь Est — —0y — средняя плотность энергии в pc стоячей волне, а p0 амплитуда давления в каждой бегущей друг навстречу другу волне.

Плоская квазистоячая волна (по терминологии работы [5]): p ₀ ( ^e ^{ik ( z +} h ) + 2 ^ cos k ( z + h ) ) , e и n — некоторые константы.

F z pr —

^p 0 ²

2pc c

F z qs

4 n x

— — E 4 п < 2 ( n 2 + ПЕ ) sin2 kh x

xf a Z Im A ") — £ ^3Re( A ⁰ ( A l + ") ' ) ) (14) V xl — 0             I — 0 ^{4 1 + 8 1 + 3} '              U

Здесь E — ^{P 0}   — средняя плотность энергии в

2 pc ²

бегущей волне.

Плоская стоячая волна 2 p ₀ cos k ( z + h ). Радиационное давление для z -компоненты равно

x ( Ё ² ( ^l + 1) ( — 1) ^l Im( A ° (Au 10 )*) + V' l —0' 4 1² + 8 1 + 3^{V 7      ( l ( l +1} ) )

+ a jT (—1)l Re (Al о)) + x l—0                  7

+ ( e ² + 2 ПЕ ) ( i            Re ( A l . ( A l + 10 ) • ) —

V l _— 0 4 1 + 8 1 + 3    \              /

Остальные компоненты силы в (14)–(16) вследствие азимутальной симметрии равны нулю. Если теперь подставить в (14)–(16) вместо A_l ⁰ их выражения через a_l и b_l из (11) и учесть оценку (12а), то окажется, что эти выражения полностью совпадут с соответствующими выражениями в работах [3–6]. Выражение (16) при этом совпадет при условии е + п = 1 Это условие необходимо для приводимости выражения p 0 ( se ik ⁽ z ⁺ h ) + 2 n cos k ( z + h ) ) к выражению, принятому в указанных работах.

ВЫВОДЫ

Таким образом, в работе показано, что общие выражения, полученные в работах [7, 8], в случае сферического включения точно совпадают с полученными для этого случая другими авторами частными результатами.

Автор благодарит Е.Д. Макарову за полезные дискуссии, приведшие, как кажется автору, к улучшению содержания статьи.

Настоящая работа выполнена при поддержке фонда РФФИ, грант № 05-03-33108 и целевой научно-технической программы Российской Федерации "Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007–2012 годы", лот 2, шифр 2007-2-2.2-04-08.