К вопросу об асимптотически сходящихся рядах

Основным инструментом решения различных высокочастотных физических задач являются асимптотические методы [1–4]. При построении асимптотических решений уравнений математической физики, например при решении задач дифракции и распространения волн, возникают асимптотически сходящиеся ряды (см. [5–7]).

Вообще говоря, асимптотически сходящиеся ряды являются расходящимися в обычном смысле, то есть частичная сумма ряда m

S m = Z U n ( X )                            (1)

n = 0

при конечном значении x стремится к бесконечности, а не к той функции f ( x ), на основе которой он построен и которую должен описывать:

m

Z u n ⁽ x ) = ” .          ⁽²⁾

n = 0

f ( x ) * lim S m = lim m ^a      m ^a

Асимптотическая сходимость предполагает, что для любого конечного значения m > M >  0 модуль разности функции и частичной суммы ряда будет меньше любого наперед заданного положительного числа ε :

• ¹    Доктор физико-математических наук, профессор, декан факультета ИСиКТ АНО ВО «Российский новый университет».

• ²    Работа выполнена при поддержке РФФИ (грант № 15-02-04206-а).

m

Z u n ⁽ x ) - ^{f (} x )

n = 0

< E .

Последнее означает, что

lim x ^a

m

f ⁽ x ) - Z u n ^{( x} )

n = 0

= 0.

Свойство (4) выполняется далеко не для всех рядов. Например, оно не имеет места для рядов Тейлора тригонометрических функций, таких, как синус и косинус, хотя эти ряды являются абсолютно сходящимися на всей вещественной оси. Конечно, свойство (4) может выполняться и для некоторых сходящихся рядов в обычном смысле, однако в данной работе мы будем называть асимптотически сходящимися рядами расходящиеся ряды (2), обладающие свойством (4).

Как уже было отмечено выше, асимптотически сходящиеся ряды используются при решении различных физических задач, однако на практике обычно ограничиваются первым приближением [5] (см. также [8–11]), то есть частичными суммами с m = 0 или m = 1. В работах рассматриваются, разумеется, конечные и не очень большие значения аргумента x , причем иногда делаются попытки учета поправок к первым приближениям [5].

ВЕСТНИК 2016

Настоящая статья посвящена анализу корректности учета последующих приближений, а также области, в которой возможен переход к асимптотике на основе численного математического моделирования. В качестве примера рассмотрим хорошо известный интеграл Френеля:

Введем функцию

i _ix ²     Г ( n + 1/2)

F⁽ x , m ) = s ( x )——= ]=; _y x ,) n„„ .    ⁽¹¹⁾

ВЕСТНИК 2016

Fr( x ) =       x e it 2 dt .                           (5)

V i n -L

Его асимптотика выписана в работах [1] в виде:

i ,_v ^Г( n + 1/2)

^Fr( x ) * ^{в (}x ) ^- T ⁶ ^^- , ,x )" 1- ,        ⁽⁶⁾

являющуюся частичной суммой ряда (6). Очевидно, что условие (4) выполняется, поскольку как интеграл Френеля, так и функция (11) при стремлении x к -да стремятся к нулю, а при стремлении x к + да - к единице.

Рассмотрим результаты численного моделирования. На рис. 1 и 2 показана амплитуда функций (5) и (10).

где 6( x ) - функция Хевисайда или, иначе, тета-функция. Формула (6) получается из интеграла (5) с применением метода стационарной фазы и интегрирования по частям. Предполагается, что ( x ²) = | x | sign x .

Очевидно, что ряд, стоящий в правой части (6), не сходится абсолютно ни при каком конечном значении x . Чтобы в этом убедиться, достаточно применить признак Д’Аламбера:

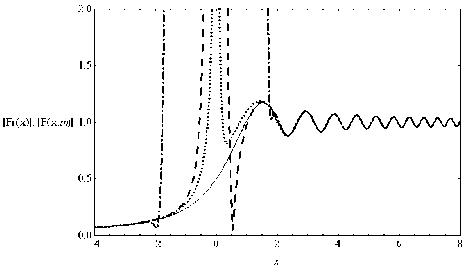
Рис. 1. График модулей интеграла Френеля и частичных сумм асимптотического ряда

u_{n + 1} ( x ) _ Г ( n + 1 + 1/2) ( ix ²) ^{n + 1/2} u_n ( x ) = ( ix ²) ^{n + 1 + 1/2} Г ( n + 1/2)

n + 1/2 ix ²

n + 1/2

Всегда можно выбрать достаточно большое n , чтобы это отношение было больше 1.

Конечно, из отсутствия абсолютной сходимости не следует, что ряд не является сходящимся, тем более, что он не является знакопостоянным и, вообще говоря, он комплексный. Однако нетрудно показать, что его общий член не стремится к нулю:

lim u_n ( x ) * 0,                                 (8)

n ^L то есть не выполняется необходимое условие сходимости. Действительно, в соответствии с формулой Стирлинга [12]:

Г ( z ) = ^ [ - 1 .                     (9)

N - V e J

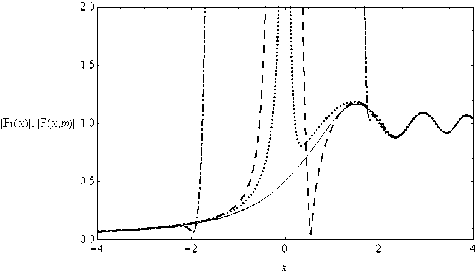
Рис. 2. График модулей интеграла Френеля и частичных сумм асимптотического ряда. Рис. 2 является фрагментом рис. 1

Тогда

lim un ( x )| = lim n ^L1       1 n ^ro	Г ( n + 1/2)	=
	( ix 2) n + 1/2

n

= ' Jn lim f n ±1/21 ^„ ,        (10)

|x V e n " V ex J поскольку числитель выражения в круглых скобках, начиная с некоторого n, всегда больше зна-

менателя.

Сплошной линией показан сам интеграл Френеля (5) (то есть, его модуль), точками – модуль первого приближения F( x , 0) , штриховой линией - модуль второго приближения F( x ,1), и, наконец, пунктиром - 1 1-е, то есть модуль F( x ,10) . Рассмотрим область «света», то есть правые части рисунков. Как и положено для асимптотик, все кривые уходят на бесконечность в окрестности нуля. Быстрее всех возвращается к исходной кривой (интегралу Френеля) первое приближение и начинает более-менее верно описывать главный максимум. Однако далее к исходной кривой эта линия приближается достаточно медленно. Второе приближение сначала формирует глубокий минимум, не имеющий ни-

каких аналогов у исходной кривой, приближается к исходной кривой значительно позже первого приближения, зато потом совпадает с исходной кривой значительно лучше. Что же касается 11-го приближения, то его встреча с исходно кривой происходит уже после прохождения главного максимума. В той же последовательности расположены приближения и в области «тени» (левые части рисунков).

На рис. 3 и рис. 4 показаны вещественные и мнимые части Сплошной интеграла Френеля (5), а также первого, второго и 11-го приближений. Обозначения те же.

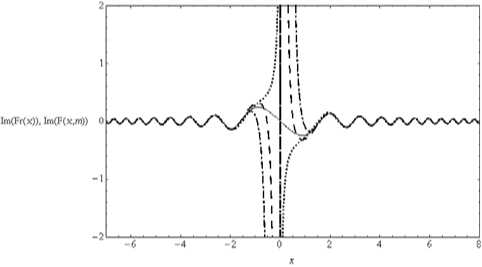
Рис. 4. График мнимых частей интеграла Френеля и частичных сумм асимптотического ряда

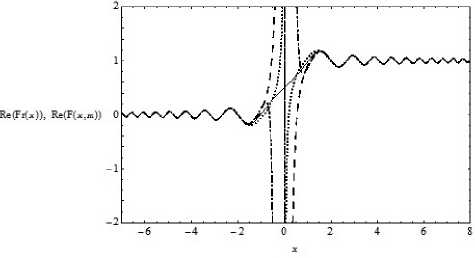
Рис. 3. График вещественных частей интеграла Френеля и частичных сумм асимптотического ряда нием m асимптотики «сползают» с кривой, описывающей интеграл Френеля.

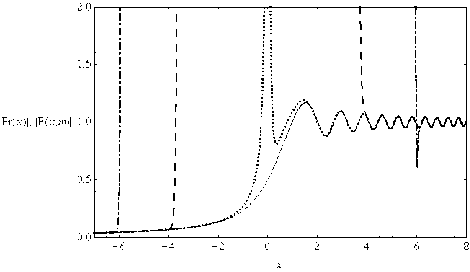
Рис. 5. График модулей интеграла Френеля и частичных сумм асимптотического ряда в случае больших значений m

На рис. 6 и 7 приведены модули разностей интеграла Френеля и асимптотического ряда для разных значений m . Точками показан модуль разности интеграла Френеля и первого приближения, штриховой линией – интеграла Френеля и второго приближения, а пунктирной линией – интеграла Френеля и 11-го приближения.

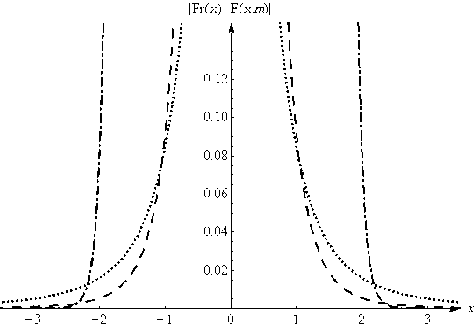
Рис. 6. График разности модулей интеграла Френеля и частичных сумм асимптотического ряда при разных значениях m

ВЕСТНИК 2016

Выводы о расходимости асимптотик и интеграла Френеля на основе сопоставления между собой вещественных и мнимых частей можно сделать такие же, как и на основе сопоставления модулей. Интересно отметь, что, в отличие от модуля, для вещественной и мнимой частей осцилляции наблюдаются не только в области «света», но и области «тени».

На рис. 5 сплошной линией по-прежнему показан модуль самого интеграла Френеля (5), точками – модуль первого приближения F( x , 0) , но штриховой линией - модуль 41-го приближения F( x , 40) , а пунктиром - модуль 101-го приближения, то есть F( x ,100) . Видно, как с увеличе-

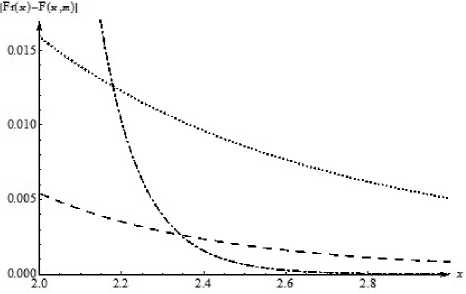
Рис. 7. График разности модулей интеграла Френеля и частичных сумм асимптотического ряда при разных значениях m . Фрагмент рис. 6

ВЕСТНИК 2016

Видно, что чем выше порядок приближения, тем позже начинается сходимость и тем энергичнее частичная сумма стремится к исходной функции. Рис. 7, являющийся фрагментом рис. 6, позволяет проследить этот процесс более подробно.

Таким образом, в работе на примере асимптотики интеграла Френеля рассмотрены свойства асимптотически сходящихся рядов (расходящихся в обычном смысле) и выявлены некоторые закономерности, касающиеся сходимости частичных сумм. Результаты работы показывают, что учет поправок к первому члену асимптотики, как неоднократно отмечалось и ранее, может не только не улучшить результат решения задачи, но в ряде случаев значительно ухудшить его [3]. Это особенно явно подтверждается сравнением поведения первого и второго приближений на приведенных выше рисунках.

Автор выражает благодарность профессору Д.С. Лукину за помощь и ценные консультации.