К вопросу об использовании байесовского метода для поиска подводных объектов

Одной из наиболее стремительно развивающихся областей археологической науки в последние десятилетия стала подводная археология, в которую входит, среди прочего, поиск и изучение затонувших кораблей. Это обусловлено, главным образом, развитием таких технических поисковых средств, как гидроакустические системы, а также подводная робототехника. Эти изменения коснулись как технического аспекта, так и экономического. В результате подводное поисковое оборудование получило широкое распространение. Сегодня оно приобретается как академическими институтами, которые ранее не имели к нему доступа, так и различными частными организациями и физическими лицами [1]. К наиболее доступному поисковому оборудованию следует отнести, в первую очередь, мобильные гидролокаторы бокового обзора (ГБО) и в виде дополнительной аппаратной функции к линейке гражданских эхолотов, и небольшие мобильные подводные аппараты. Археологические исследования затонувших судов имеют значительную актуальность как с теоретической, так и с практической точек зрения [2–4]. В качестве исторических объектов затонувшие корабли часто предоставляют исследователям уникальную возможность получить оригинальные сведения о материальной культуре прошлого; в некоторых случаях, помимо материальных источников, удается получить даже документальные свидетельства. С другой стороны, исследование кораблекрушений представляется важной прикладной задачей, связанной с решением проблем очистки акваторий водных путей от физических препятствий, каковыми могут быть затонувшие суда. Еще одной немаловажной задачей является экологический мониторинг акватории водоемов: суда, особенно промышленной эпохи, могут представлять угрозу для окружающей среды содержанием своих трюмов, в которых может быть токсичный груз, или самим судном и его топливом. В связи с этим поиски и исследования затонувших судов являются важнейшими научными задачами.

Несмотря на применение разнообразного поискового оборудования, позволяющего, как в случае ГБО, охватывать внушительные площади донной поверхности, установление местоположения затонувших кораблей остается сложной процедурой. Даже в случае, когда географические координаты затопления известны, обнаружить подводный объект не всегда удается, а, учитывая высокую стоимость поисковых работ, аренду исследовательского судна, расходов, связанных с эксплуатацией оборудования и работы специалистов, время для проведения поле- вых работ может быть весьма ограничено. Препятствием к проведению исследований могут стать географические и метеорологические факторы. В связи с этим требуется создание эффективной методики поиска, в рамках которой можно предварительно сузить зону поиска до районов, где нахождение затонувшего корабля наиболее вероятно.

Одним из наиболее перспективных подходов, реализующих математическую модель для определения местоположения затонувших кораблей, следует считать байесовский поисковый метод. Свое название он получил по имени английского математика XVIII в. Томаса Байеса, известного своими работами в области теории вероятности и математической статистики. Теорема Байеса хорошо известна и имеет следующий вид

P ( A | B ) =

P ( B | A ) P ( A ) P ( B )

где P ( A ) – априорное предположением вероятности того или иного события; P ( A|B ) – вероятность того, что A верно при условии апостериорной вероятности; P ( В|А ) – вероятность того, что B произойдет в случае верности A ; в этом случае P ( B ) является гарантией того, что произойдет событие B .

Байесовский метод поиска нашел достаточно продуктивное применение в ряде зарубежных поисковых проектов. Одним из наиболее известных случаев применения данного метода являются поиски американской атомной подводной лодки USS Scorpion, затонувшей в результате аварии в 1964 г. В результате применения указанного метода, многокилометровую зону поиска в Северной Атлантике удалось сузить до 300 м2 [5]. Еще одним значимым достижением данного метода стало обнаружение затонувшего в 1857 г. американского пассажирского парохода Central America. Местоположение затопления судна было известно только приблизительно, поскольку авария произошла во время шторма и у экипажа не было возможности точно определить координаты судна. Кроме того, большая глубина привела к тому, что судно находилось на существенном расстоянии от места, где корабль предположительно затонул. Карта поиска, с определением вероятности нахождения судна (от 0 до 65 %) представлена на рис. 1.

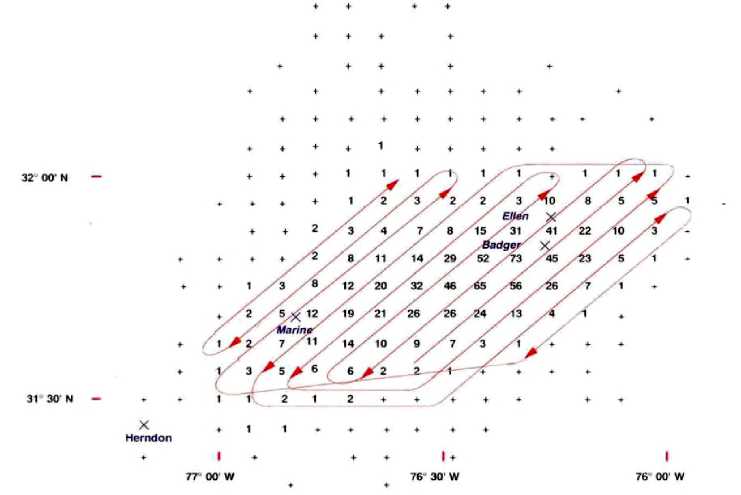
Рис. 1. Графическая модель плотности вероятности поиска парохода Central America, нанесенная на координатную сетку [6]

Fig. 1. Graphic search model for the probability distribution function for the SS Central American [6]

Таким образом, мы видим, что байесовский метод может оказаться весьма результативным при поиске затонувших кораблей. В целом, он является одним из немногих теоретических методов, отвечающих задачам, рассматриваемым в рамках настоящей работы. Как показывает практика, поиск затонувших судов, особенно в прибрежных морских зонах и внутренних водоемах, ведется, главным образом, бессистемно: известные координаты вводятся в картографические программы спутниковой навигации с целью произведения поиска in situ . Такой подход возлагает большую нагрузку на человеческого оператора зондирующих устройств, требуя от него высокого профессионализма и физической нагрузки. В результате поисковые работы зачастую оказываются нерезультативными. Снижение концентрации внимания оператора в результате долгой монотонной работы может привести к тому, что объект оказывается пропущенным и обнаруженным только во время камеральной обработки материалов. Несмотря на очевидную потребность эффективного поискового метода, применение байесовского метода для поиска затонувших судов продолжает оставаться слабоизученной темой. Так, в отечественной научной литературе удалось установить всего лишь одну статью по данной проблематике [7]. Немного лучше дела обстоят в зарубежной литературе [8–10], однако и данные мвтериалы нельзя считать удовлетворительными поскольку до сих пор не существует специализированных программных средств, позволяющих внедрять байесовский поисковый метод на практике. Расчеты производятся вручную и, как правило, относительно уже найденных объектов, что имеет только теоретическую значимость.

Метод байесовского поиска

Метод байесовского поиска достаточно прост, что обусловлено исходной вероятностной модели. Метод является частным случает теории принятия решений и как таковой может строиться на совокупности объективных и субъективных данных, позволяя принять оптимальное решение. Как и во многих поисковых задачах, предположение строится на основе ограниченного количества данных; качество этих данных также может оказаться невысоким.

Итак, первой задачей является построение априорного распределения, для чего имеющиеся данные, в том числе неполные и фрагментарные, необходимо упорядочить в последовательные множенства, под которыми будут пониматься вероятностные сценарии. Затем необходимо придать количественную оценку неопределенностям путем определения их вероятностного фактора. Эта задача выполняется путем определения вероятности конкретного сценария, а также введением в расчет субъективных факторов. Далее необходимо рассчитать вероятностное распределение для каждого из сценариев, объединив расчеты в априорные веса (вероятности того или иного сценария). Для этого при построении поисковой модели необходимо учесть (при наличии) результаты предшествующих поисковых работ. Отметим, что даже в случае построения модели исключительно на основе объективных и точных данных, полученное распределение будет считаться лишь предположением до момента доказательства его истинности. Для байесовской модели, как и для любой статистической модели, характерным является отражение индивидуальности принятого решения, сделанного на основе наилучшего понимания задачи, а также с учетом результатов предшествующих поисков. Однако необходимо учесть, что каждый отдельный поиск является индивидуальным случаем, который нельзя воспроизвести многократно для получения эмпирического вероятностного распределения.

Обратимся к факторам, обеспечивающим эффективность байесовского поиска как метода, позволяющего:

• –    обеспечить принципиально новый подход, включающий в себя все объективные и субъективные данные о местоположении затонувшего судна с целью построения функции распределения вероятностей о нахождении объекта;

• –    построить функцию распределения вероятностей для сужения поисковой зоны с целью повышения эффективности поиска;

• –    включать в модель новые данные о поиске, в том числе неудачные поисковые работы, для построения апостериорной функции распределения вероятностей, что лежит в основе построения последующих поисковых маршрутов;

• –    получать аналитические расчеты поискового процесса с целью достижения заданного уровня эффективности последних поисковых мероприятий [9].

Необходимым условием формирования поисковой модели является создание базы данных, которая будет служить ее основой: она может иметь различные виды и формы в зависимости от требований поисковый модели, а также автономности ее работы, поэтому рассмотрим здесь лишь ее содержание. Сведения относительно технических характеристик того или иного корабля могут быть получены как из неопубликованных исторических источников (архивные данные), так и опубликованных. К последним относятся различные морские статистические сборники, содержащие сведения о технических характеристиках кораблей [10]. Отметим, что некоторые суда строились по типовым проектам, следовательно, достаточно учесть характеристики проектов данного типа для организации поисковых работ. В целом, к данному блоку сведений относятся следующие параметры: длина, тип движителя (судно могло быть самоходное или несамоходное, моторное или парусное, и др.), тип груза и его количество, грузоподъемность. В некоторых случаях можно учитывать вид надстройки, материал изготовления корпуса, количество и типы машин и прочее. Однако, как показывает практика, данные параметры не всегда являются важными для проведения поиска. Важнейшими являются сведениями о скорости и направлении движения судна, записи из судового журнала о положении корабля в момент гибели (этот параметр в отношении исторических судов построен, главным образом, на основе данных счисления, а не астрономических наблюдений).

Отдельным блоком являются данные географического характера: глубина, скорость и направление течения, геоморфологические особенности дна акватории, близость суши, направление ветра, метеорологические условия и другие параметры [11]. Сведения, полученные в ходе поисковых работ, вносятся в базу данных с целью корректировки поисковой модели (рис. 2) [12]. Сюда следует отнести данные, полученные, в том числе, и с применением метода дистанционного зондирования (аэрофотосъемки и космического ДЗЗ). Отметим, что к отдельной задаче следует отнести корректировку географических координат, полученных по данным спутниковых систем навигации.

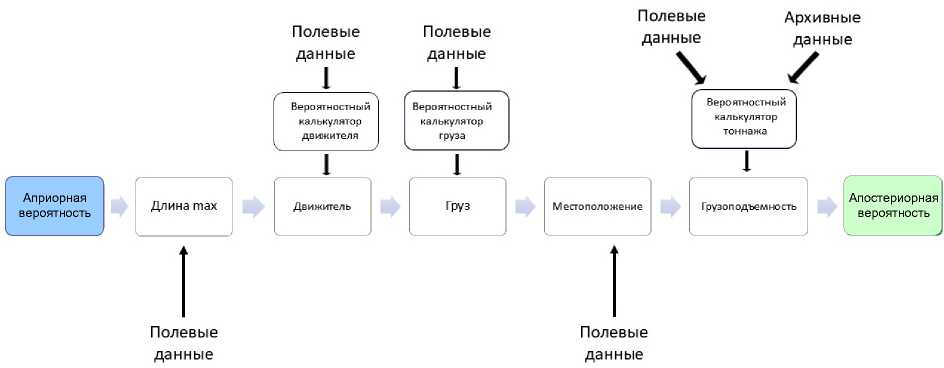
Рис. 2. Схема данных в предполагаемой базе

Fig. 2. Diagram of data input in Bayesian model data base

Ниже представлена схема базы данных, построенная на основе метода, предложенного в работе [12]. Она представляет собой байесовский метод определения вероятности обнаружения того или иного исторического судна на основе априорной вероятности. В ходе работы модели происходит ее насыщение фактическими данными, в том числе полевыми, что позволяет вывести апостериорную вероятность идентификации судна. Предложенный метод представлен в одной из наиболее оригинальных работ, посвященных системе байесовского поиска затонув- ших судов. В отличие от схожих тематических публикаций, автором работы предложен метод не определения местонахождения судна, а его идентификации. Данная задача является актуальной, поскольку в местах активного судоходства и глубоководных акваториях в одной и той же точке может находиться множество судов одновременно. Сочетания предложенного подхода с классическим методом байесовского поиска позволяет повысить вероятность обнаружения конкретного судна.

Проблема локализации. Случай «Тбилиси» 2024 г.

Летом 2024 г. группа исследователей, куда входили представители Русского географического общества, а также Сибирского государственного университета науки и технологий имени академика М. Ф. Решетнева (г. Красноярск), приняла участие в поисковой экспедиции в Енисейском заливе (район Крестовских островов) с целью обнаружения останков транспорта «Тбилиси» (капитан В. К. Субботин). Это судно входило в состав небольшого арктического конвоя, следовавшего из Дудинки в Диксон в сентябре 1943 г. При подходе к Малому Крестовскому острову судно подорвалось на немецкой магнитной мине, поставленной ранее подводной лодкой U-636, и затонуло. В судовом журнале координаты гибели судна были записаны, как N 72°25', E 80°36'. Проект по организации поиска и обследования судна, представляющего собой уникальный исторический памятник боевым действиям в ходе Великой Отечественной войны (1941–1945 гг.), разрабатывался в течение нескольких лет. В конечном варианте проект был представлен как краткосрочная поисковая экспедиция, основными методами поиска которой были ГБО, системы спутникового позиционирования и дистанционного зондирования земли, а также беспилотный летательный аппарат. В случае обнаружения судна, его исследования должны были продолжить аквалангисты.

С учетом известных координат объекта зона поиска представляла собой квадрат со сторонами около 1,3 км, что составляло приблизительно 1,7 км2. Глубины в зоне поиска постоянны и составляют в среднем около 12 м, что позволяет настраивать дальность бортового луча ГБО, работающего в мегагерцовом диапазоне, на 30–40 м. Для того чтобы полностью охватить изучаемую область акватории (с перекрытием зоны акустической тени), с учетом рекомендованной скорости движения буксируемого измерительного преобразователя от 1,5 до 3 kn, потребуется приблизительно 3–4 ч. Это условие не всегда возможно выполнить, например, по причине плохих погодных условий. Кроме того, ввиду высокой стоимости фрахтования судна, с которого происходил поиск, на все поисковые работы было отведено не более 1,5 суток.

Опыт оператора ГБО позволил определить точное местоположение кораблекрушения по истечению 3,5 ч поисковых работ с борта маломерного судна. Последующие погружения к кораблю позволили его точно идентифицировать. Маршрут поиска ГБО по причине сильного ветра и большой волны (1–1,5 м) был построен в виде концентрических кругов, что противоречит традиционной методике поиска, каковой являются галсовые проходы. Однако направления ветра и волн не позволили использовать данную методику. Очевидно, что описанный метод поиска не может считаться эффективным, поскольку полагается исключительно на опыт оператора ГБО, а также на случай. Поэтому, рассмотрим организацию поисковых работ по поиску «Тбилиси» с использование метода Байеса.

Математическая модель Байеса

Для построения поисковой модели необходимо выполнить следующие шаги:

• – выдвинуть наиболее вероятные гипотезы о том, что могло произойти с судном (количество гипотез не ограничено);

  – для каждой из гипотез необходимо построить функции плотности вероятности для местонахождения объекта;

  – построить функцию вероятности нахождения кораблекрушения в заданной точке X при проведении поиска в заданной точке. Необходимо учесть, что при проведении поисковых работ в зонах с большими глубинами, данная функция отражает глубину. В случае проведения поис-

• ков на мелководье, вероятность обнаружения объекта существенно возрастает, поскольку судно лежит на дне приблизительно в том же месте, где произошло погружение;

  – использовать представленную выше информацию для построения графической модели плотности вероятности, что предполагает умножение двух функций. Таким образом, нахождение кораблекрушения в точке Х для всех точек Х;

  – далее построить поисковый маршрут от точек с наибольшей вероятностью к точкам с наименьшей;

  – систематически пересматривать все новые вероятности в ходе поиска. Так, если в предполагаемой точки X в результате поисковых работ, например, гидролокатором бокового обзора, не было обнаружено никаких обломков корабля, то вероятность нахождения судна в этой точке должна быть существенно снижена, в то время как вероятность для других точек должна возрасти.

Представим себе зону поиска, разбитую на сетку, где вероятность нахождения затонувшего судна в каждой из квадратов выражается P . Истинность данного предположения выражается Y . В случае если судно не обнаружено в заданном квадрате, то согласно теореме Байеса, скорректированная вероятность будет:

P =--- (—)— = P ---< P .

(1 - P ) + P (1 - Y )    1 - PY

В случае если априорная вероятность r для каждого квадрата истинна, то вероятность апостериорная будет выражаться следующим образом:

r'

= r----- 1 - PY

> r .

Рассмотрим практический метод данного подхода в отношении поиска судна с известными параметрами (характеристики судна, геофизические факторы и другие известные переменные) на примере [13; 14].

Первым действием будет разбиение поисковой зоны на квадраты.

i = 1	2	3	4	5
6	7

Далее представим, что вероятность обнаружения объекта имеет вид Pr ( Z_i = 1| Y_i = 1), где i – индекс квадрата; Z_i – результаты поиска в i-й ячейке; Y_i – истинное положение подводного объекта в i-й ячейке (единица означает, что объект найден): в этом случае Pr ( Y_i = 1). Необходимо учитывать, что объект может отсутствовать в заданном квадрате, что может быть выявлено в ходе его обследования.

Теперь рассмотрим метод Байеса применительно к поискам «Тбилиси». Разобьем зону поиска (1,69 км2) на квадратную сетку, состоящую из 16 квадратов, каждый из которых ≈105,62, что вполне удовлетворительно, учитывая длину судна более 100 м (рис. 3, а). Центр сетки разместим на точке с известными историческими координатами. Определим наибольшую вероятность нахождения судная в четырех центральных квадратах – 0,17, а, наименьшую – 0,01. Аналогичным образом построим карту вероятностей по глубинам заданной местности с вероятностями от 0,29 (min) до 0,98 (max). Зная, что средняя глубина в поисковой зоне 12 м, квадраты с наи- меньшими глубинами будут представлять большую вероятность нахождения в них судна. Сочетав эти значения, получим новые показатели вероятности для каждого квадрата (рис. 3, б).

0,02	0,02	0,02	0,01
0,08	0,17	0,17	0,01
0,08	0,17	0,17	0,01
0,02	0,02	0,02	0,01

а

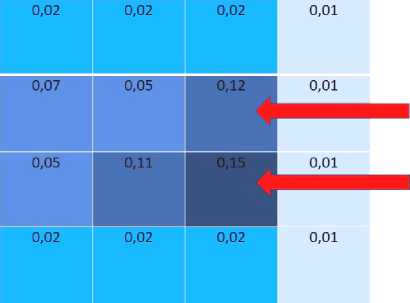
б

Рис. 3. Сетка распределения вероятностей: а – априорная; б – апостериорная с учетом глубин акватории

Fig. 3. Probability density map: а – prior; б – posterior based on depth map

Как видно, наиболее вероятными квадратами были 0,12 и 0,15 (обозначены стрелками). Начав поиски с нижнего квадрата, удалось установить, что корабля здесь нет. В связи с этим уточним вероятностную модель с учетом этих данных:

p[ qin ] = зе кк д ц е в, (1 - P [ Q ] + P [ Q ])(1 - PYQ ])

где Q – предположительное наличие объекта; N – отсутствие объекта; Y – обнаружение объекта.

P [ Q ] и P [ Y / Q ] являются вероятностями, выведенными из построенных сеток.

Уточненная вероятность для квадрата 0,15 с учетом заданной глубины 0,86, получим:

P[Q\N ] =

0,17(1 — 0,86)

, *

(1 - 0,17) + 0,17(1 - 0,86)

Таким образом, вероятность нахождения «Тбилиси» в квадрате 0,17 изменилась (с учетом глубины) до 0,15, а затем до 0,03. Это, в свою очередь, повышает вероятность нахождения корабля в других квадратах:

P [ Q ] =

P [ Q ]

(1 - P [ Q ]) + p ( Q ) • (1 - P [ N\Q ])’

Так, вероятность нахождения объекта в соседних квадратах увеличивается до 0,12 и 0,13 соответственно. Далее поиск продолжается, изучая, в первую очередь, квадраты с наибольшей вероятностью. Результат поиска представлена на рис. 4. Как видно, судно удалось обнаружить в квадрате, в котором априорная вероятность (большая глубина) была занижена до показателя 0,05. Оказалось, что глубины на лоциях этого района даны без учета нахождения затонувшего судна, что в данном конкретном случае сводило фактор глубины до малозначимого. На практике начинать поиски с квадрата, имеющего наибольшую вероятность нахождения объекта, не всегда наиболее эффективно, поскольку чтобы до него добраться необходимо сначала пройти все остальные квадраты, поэтому при построении маршрута поиска следует начать с прилегающих квадратов, где вероятность нахождения объекта более низкая: тем более, что, как видно из рис. 4, существует вероятность обнаружения обломков судна в прилегающих квадратах.

Это, безусловно, увеличит шансы обнаружить затонувшее судно. Тем не менее применение байесовского поиска позволяет выстроить наиболее адекватный маршрут поиска с включением в него необходимых факторов.

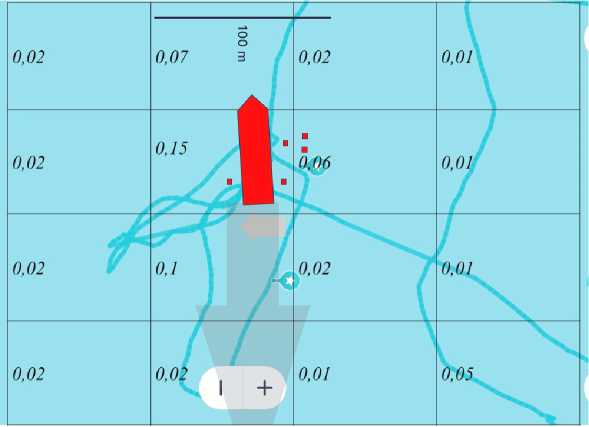
Рис. 4. Зона поиска транспорта «Тбилиси» с нанесением на нее сетки распределения вероятностей. Пятиугольник – обозначает судно, а квадраты – обломки

Fig. 4. Search area of the SS Tbilisi with an overlaying probability density map. The shapes represent the vessel and scatted debris on the seabed

Заключение

В результате применения байесовской системы поиска затонувших судов, можно существенно повысить эффективность поиска затонувших судов, причем сделать это заблаговременно. Ряд параметров, рассматриваемых в классических моделях (например, глубину), при этом можно исключить. В систему поиска можно вносить дополнительные параметры подводного объекта, позволяющие не только повысить вероятность его нахождения, но и его идентификации. Если размеры судна являются основным фактором, позволяющим его обнаружить, то такие характеристики, как тип судна и его движителя (самоходное/ несамоходное/ парусное/ моторное) служат дополнительными факторами, способствующими его идентификации. При этом, в случае отсутствия сведений о корпусе судна либо его разложении, данный фактор, а также сведения о силовых установках судна (котлах) и типе механического движителя (винт, гребное колесо) становятся основными параметрами, определяющими вероятность его обнаружения или идентификации. Таким образом, удалось удачно сочетать два направления в философии байесовского поиска затонувших судов. Дальнейшее развитие данного метода представлено в [15–16] и заключается в создании эффективной программной среды, позволяющей интегрировать обновляющиеся базы данных по подводным объектам, новые полученные геоданные, в том числе с ГБО и других систем дистанционного зондирования, включающие в себя системы дистанционного зондирования земли. В дальнейших исследованиях мы планирует обратиться к созданию подобной среды, используя за основу такие инструменты статистического анализа, как JASP.