К вопросу об изучении темы "Четырехугольники" в школьном курсе математики

Четырехугольники – является одним из основных материалом для изучения курса планиметрии. Четырехугольник объясняется в одних учебниках как некоторая замкнутая ломаная, а в других - как часть плоскости, ограниченная такой ломаной. Во всех используемых в настоящее время учебниках осуществляется похожий подход во введении частных видов параллелограммов: ромбов и прямоугольников. Квадрат в одних учебниках определяется как четырехугольник, который является одновременно и прямоугольником и ромбом. В других квадрат рассматривается как частный вид прямоугольника. Трапецияизучается только после изучения параллелограммов.

Введение определения четырехугольника вводится учителем только тогда, когда уже изучено понятие многоугольника. Л.С. Атанасян вводит понятие четырехугольник как отдельный вид многоугольника; А.В. Погорелов данное понятие вводит позднее.

Четырехугольником называется фигура, которая состоит из четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называют вершинами четырехугольника, а соединяющие их отрезки – сторонами четырехугольника. Две несмежные стороны четырехугольника называются противоположными.

Четырехугольники бывают выпуклые и невыпуклые. Каждая диагональ выпуклого четырехугольника разделяет    его на два треугольника. Одна из диагоналей невыпуклого четырехугольника также разделяет его на 2 треугольника.

Так как сумма углов выпуклого n-угольника равна 180 градусов, то сумма углов выпуклого четырехугольника равна 360 градусов.

Для закрепления представленного материала, учащимся предлагается решить простейшую задачу по теме.

Задача №1. На рисунках изображены 3 фигуры, каждая из них состоит из 4 точек и 4 последовательно соединяющих их отрезков. Какие из представленных фигур являются четырехугольником? ( Устное решение задачи).

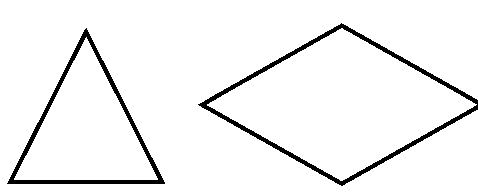
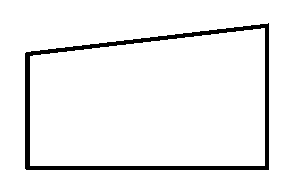
При рассмотрении различных свойств и признаков параллелограмма широко используются свойства и признаки равных треугольников, свойства углов, которые образовались при пересечении двух параллельных прямых третьей, признаки параллельности прямых.

Материал о параллелограммах и их частных видах удобен для формирования и развития логического мышления учащихся. Здесь учителюпредоставляются широкие возможности по работе с определениями: например, предложить ученику дать определение прямоугольника через понятие параллелограмма, прямоугольника и т.д.

В теме «четырехугольники» формируются понятия и определения основных видов четырехугольников, учащиеся знакомятся с основными методами решения задач и решают задачи каждого вида. В процессе изучения материала необходимо добиться, чтобы все учащиеся овладели необходимыми знаниями и умениями, которые будут необходимы при дальнейшем изучении геометрии. В этом случае учитель должен как можно тщательнее анализировать и подбирать учебный материал. Нельзя забывать и о самостоятельной работе учащихся и отводить больше времени для творческой деятельности школьников. Все эти средства будут способствовать максимальному усвоению материала учениками.