К вопросу об определении энергетических характеристик машины двойного питания в режиме колебательного движения

В различных отраслях народного хозяйства в качестве источников колебательного усилия или перемещения все большее применение находят электроприводы колебательного движения (ЭКД), выполненные на базе асинхронных машин (АД), работающих непосредственно в режиме вынужденных колебаний за счет различных видов модуляции питающих напряжений (токов). Такие электроприводы позволяют без дополнительных звеньев преобразования движения обеспечить непосредственно на ходу регулируемые по частоте, амплитуде и форме колебания рабочего органа привода в самом широком диапазоне требуемых нагрузок [1].

Однако, как показывают результаты их практического применения, несмотря на всю простоту технической реализации, энергетические характеристики безредукторных КЭП на основе АД значительно уступают приводам, выполненным, например, по принципу слежения за периодическим сигналом или использующие самореверс [2–4].

Одним из возможных путей повышения энергетических показателей безредукторных электроприводов, работающих непосредственно в режиме периодического движения, является использование в них в качестве исполнительного двигателя машины двойного питания (МДП) [5]. Как показывают проведенные исследования, такие КЭП позволяют почти в два раза улучшить не только энергетические, но и динамические характеристики электропривода благодаря возможности работать МДП как в асинхронном, так и квазисинхрон-ном режимах [6, 7].

В данной работе предлагается оценку энергетических возможностей МДП в режиме периодического движения проводить на основании анализа потребляемой и выходной мощностей. Так как в общем случае данные характеристики имеют периодический характер, то согласно рекомендациям [8], будем их оценивать максимальными, среднеквадратичными или мгновенными величинами.

Теоретическая часть

Полная работа, совершаемая МДП в режиме периодического движения при незатухающих колебаниях и с учетом наличия в системе диссипации (жидкостного трения), описывается выражением

E = JMэм (t)dX = JMэм (tMt)dt , где Мэм(t) – колебательный электромагнитный момент, развиваемый МДП; to(t) = dx/dt, x(t) — скорость и закон движения подвижного элемента двигателя.

Считая закон движения подвижного элемента привода χ( t ) гармонической функцией времени X(t) = X _m sin( Q t + а) и ограничиваясь первым приближением колебательного электромагнитного момента М _эм( t ), величину мгновенной механической мощности двигателя можно определить как

_D dE M эм, m to m ^sin( Q^{-a )}

Рмех (t) = — =--------^

dt2

_r               , M „_{M m}to_m cos( Q-a )

эм, m m

x[1 + cos 2(Q t + a)] +,------ x sin2(Q t + a),(1)

где М _эм , _m , to _m - амплитудные значения колебательного электромагнитного момента и скорости МДП; φ, α – начальные фазы колебательного электромагнитного момента и закона движения подвижного элемента двигателя; Ω – угловая частота колебаний.

Анализируя полученное выражение (1), можно заключить, что мгновенное значение механической мощности, развиваемой МДП при работе в режиме вынужденных колебаний, содержит две составляющие: активную и реактивную. Поскольку каждая из них вносит свой весовой вклад и является необходимой, предписанной данному физическому процессу, то оценку выходной мощно- сти КЭП в дальнейшем будем проводить по величине полной колебательной мощности мех,акт + Pмех,реак   0,5Mэм,m ®m ,

где активная и реактивная составляющие мощно- сти определяются как

^P мех,акт = 0, ⁵ M эм, m ^ m ^sin( Ф ^- «X

^P мех,реак = ^0,5 M эм, m ® m ^cos( V^-a ).

Отметим, что полученные выражения (2), (3) являются приближенными, так как не учитывают при расчетах составляющие мощности искажения. Тем не менее, они могут быть рекомендованы на этапе предварительного расчета при оценке предельных характеристик и выборе исполнительного двигателя [9].

Более точно величина полной выходной мощности может быть определена через квадратичные значения электромагнитного усилия и колебательной скорости:

М ср.кв

ω ср.кв

₁ t + T

1     M эм ( t )² dt ;

tt

\ t + T

1    ω( t )² dt ;

t _t

P M_Lex   ⁰,⁵ M ср.кв ® ср.кв ^.

Следует учесть, что при расчетах по представленным интегральным выражениям (2), (4) потреблению реактивной механической мощности будет соответствовать положительное значение Р мех,реакт , а генерированию – отрицательное, что говорит о двигательном и генераторном режимах работы двигателя в течение одного периода колебания подвижного элемента.

Исходя из того, что обобщенная нагрузка ЭКД в большинстве случаев может быть представ- лена как

Mн(t) = Lмех d2X + Rmех   + См!х, dt2 dt где Lмех , Rмех , Cме1х – коэффициенты инерционного, демпфирующего и позиционного усилия нагрузки. Учитывая, что развиваемый МДП электромагнитный момент содержит пусковую fm1, демпфирующую fm2 и позиционные fm0 составляющие, среднее значение выходной мощности, отдаваемой в нагрузку за период колебаний Т, будет определяться постоянной составляющей активной части мгновенной механической мощности как t+T

Р мех,ср = 7 f M эм ( t М t ) dt =

, tt л .    Оfmj(Смех -L ..М 1 + R.U

= 0,5--:----и-------—----------- —х

( С мех + f m 2 - L мех ^) 2 + ( R мех - f m о ) 2 ^

х sin( Q-a ).

При этом средняя за период колебания Т величина реактивной составляющей будет соответствовать нулю. Последнее говорит о полном перераспределении реактивной мощности в течение периода из двигателя в нагрузку и наоборот.

Анализ полученного выражения позволяет сделать вывод о том, что даже при отсутствии в электромеханической колебательной системе позиционной нагрузки ( С мех = 0) в электроприводе с МДП может быть достигнут резонансный режим работы при условии f_{m 2} - L _мех О ² = 0. В этом случае электропривод будет обладать максимальными выходными параметрами и располагать при нулевом демпфировании ( R мех =0) максимальными значениями полной и средней механическими мощностями

Р мех.ср

f ^C L мех О ²)² + R M ех Q ² . ² ^R мех

С целью дальнейшей оценки энергетических показателей качества необходимо определить мгновенные значения потребляемых исполнительным двигателем мощностей по обмоткам статора и ротора. Последние определятся как

Pn (t) = Un (t) in (t), где n – номер соответствующего фазного тока in(t) и напряжения Un(t).

Тогда в системе фазных координат α–β мгновенные значения мощностей при фазовом способе возбуждения колебательного режима работы за счет разночастотного питания обмоток МДП можно записать как

7 0 s ( t ) = P 1 [ 1 - cos2(a i t + 0 1 ) ] - Q 1 sin2(a>₁ t + 0 1 ) - T 1 ;

P's (t ) = P 2 [ 1 - cos 2(m 2 1 + 0 2 ) ] - Q ₂ sin2(ro 2 1 + 0 2 ) - T ₂;

P ar^(t ) = { P 3 [ 1 ^- cos ²⁽ ® 1 ^{t + 0}3 ) ] ^c osX +

+ P 3 [ 1 - cos 2(m₂ 1 + 0 4 ) ] sinx } -

- { Q 3 sin2(a i t + 0₃)cosx + Q sin2(w₂ 1 + 0 4 )sinx } - T 3 ;

P p r ( t ) = { P 4 [ 1 - cos 2(^ i t + 6 3 ) ] sinx +

+ P₄ [ 1 - cos 2(m₂ 1 + 0 4 ) ] cos x } -

-{Q4 sin 2(to11 + 03) sin x+Q4 sin 2(m21 + 04) cos x} - T4, где Pn, Pn, Qn, Qn, Tn - соответственно актив- ные, реактивные мощности и мощности искажения; ω1, ω2, θn – циклические частоты и фазы питающих напряжений, причем ω2 = ω1 +Ω.

Заметим, что появление мощностей искажения Т n в мгновенных значениях потребляемых мощностей вызвано, в первую очередь, наличием внутренней электромеханической связи между фазными обмотками двигателя, а не искажением формы тока МДП, как это имеет место в известном смысле [7], вследствие существенной нелинейности ее параметров.

Электроэнергетика

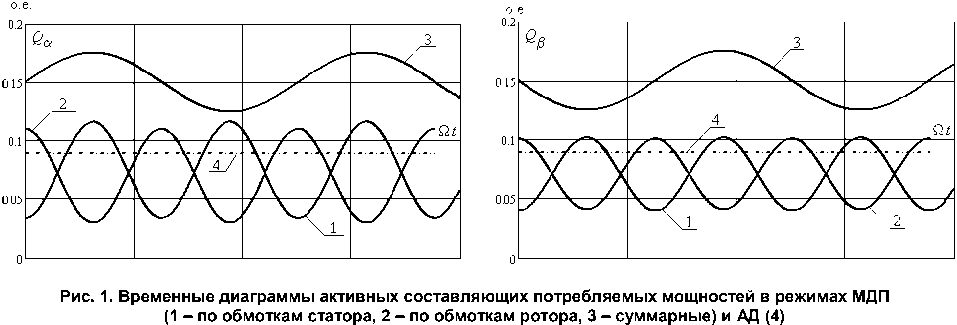
Если оценить значения суммарных потребляемых по осям а и р активных и реактивных мощностей:

р =р + р • 0=0 + 0 ■ α     α s α r ; α      α s     α r ;

Ре = Ре, + Ре r; Qe = Qe. + Qe r, то можно отметить, что потребление активных мощностей происходит только по роторным цепям, в то время как статорные обмотки МДП в режиме периодического движения рекуперируют энергию в питающую сеть. В связи с этим мощности Рas и Ррs имеют отрицательные значения. В результате при использовании в КЭП в качестве исполнительного двигателя МДП, наблюдается общее снижение потребляемой активной мощности (почти в 2 раза, по сравнению с АД) при существенном увеличении выходной мощности. Рис. 1 иллюстрирует данные выводы.

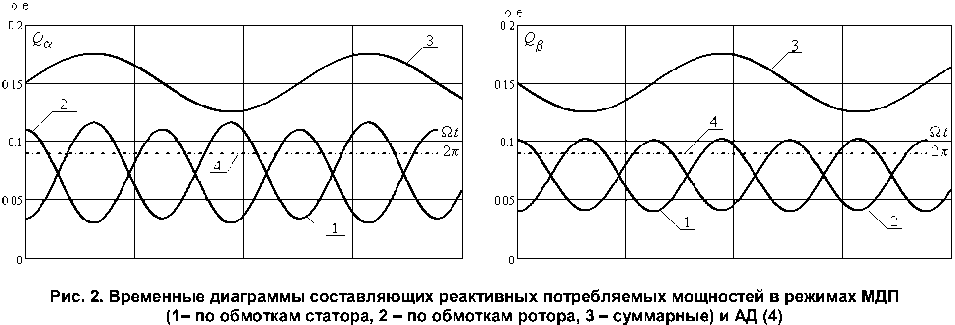
Что же касается суммарных реактивных мощностей, то в режиме МДП их значение выше из-за необходимости дополнительных затрат на формирование магнитных полей обмоток ротора (рис. 2).

Средние за период колебания значения активных и реактивных мощностей, потребляемые статорными обмотками, описываются выражениями:

1 t + т

Раз СП        ( Раз ( t ) dt ;

α s ,ср             α s

t

I t + т Р в s ,ср = т J Р в s ( t ) dt ;

Q^ ср = — + иаз^^ dt ;

V 0^{s ,ср}    т _Ю1 J    a s    dt ,

1 t + ^т     din _s ( t )

Qb3  = Ufi_s ~^d-dt .

v^в s .ср    т _m 2 j   p s    dt

Их мгновенные значения при фазовой модуляции питающих напряжений представлены таблице.

Из выражений (6) с учетом таблицы видно, что средние значения мощностей зависят от величины времени t. Это говорит о том, что в общем случае энергетические характеристики МДП в режиме колебательного движения являются почти периодическими функциями [10]. Поскольку кратность несущей и модулирующих частот Q / m 1 в общем случае является иррациональным числом, то предлагается определять их величины приближенно, либо для конкретного заданного интервала времени ∆ t = t 1 + T .

Полученные выражения (2)–(4), (6) являются теоретической основой для анализа и оценки энергетических возможностей МДП при работе в ре-

Составляющие активных и реактивных мощностей

р αs,ср P _ Р1й 1 4пю1 sin 2(— t + 9] )(cos 4n — -1) + sin 4n—cos 2(Ю] t + 9 О       О 1) ; + + ж 4πω1 _С0 s 2(ю1t + 91 )(cos 4п —1 -1) - sin 4n—1sin2(—11 + 91) βs,ср P2 - ^О. 4πω2 Юэ sin 2(ю2 t + 92 )(cos 4n   - . . Юэ 1) + sin 4n "^2" cos 2(ю2 t + 92) + + Q2й 4πω2 Юэ cos 2(ю2 t + 92 )(cos 4п -^- -1) ω - sin 4n   sin 2(ю2t + 92 *. Qαs,ср Q _ 61° 61 4пю1 sin 2(Ю[ t + 9j )(cos 4n ^1 -1) + sin 4n—cos 2(ю tt + 91) _               О         О - SL 4пю1 cos 2(ю1t + 91 )(cos 4п — -1) - sin 4n —- sin 2(—11 + 91) ; Qβs,ср п Q2 й Q2 4πω2 Ю, sin 2(ю2 t + 92 )(cos 4n — - 1) + sin 4n—-cos2(—21 + 92) P2 О 4πω2 .Ю- „ cos 2(ю2 t + 92 )(cos 4п — -1) Юэ - sin 4n-^-sin2(—21 + 92) жиме вынужденных колебаний, что позволяет оп- тимизировать электропривод по энергетическому критерию – обобщенному коэффициенту полезного действия, который без учета мощности искаже- ния определяется как

П E =

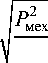
мех,реак

S ²

где 5 = рРд+ + Q2, — условно потребляемая двигате лем полная мощность; Рдв = £ Pn , Qдв = £ Q,ср.

n = 1 n = 1

Результаты проведенных исследований показали, что при изменении коэффициента нагрузки Z мех ^{( О )} = ( С _м ех — С мех ^ 2 )/ ^ мех ° , обобщенный ^коэф фициент полезного действия η Е имеет свое максимальное значение при электромеханическом резонансе и определяется в основном характером изменения активной составляющей выходной мощности Р мех,акт несмотря на то, что общая механическая мощность Р мех имеет свое максимальное значения в до- и зарезонансных режимах работы (см. рис. 2).

Результаты расчетов показали, что обобщенный коэффициент полезного действия МДП в два раза больше чем у АД, работающего в колебательном режиме, и стремится к значению номинального КПД АД, работающего в режиме однонаправленного движения.

Заключение

• 1.    Оценку энергетических характеристик МДП, работающей в режиме колебательного движения

• 2.    Полученные выражения для энергетических характеристик позволяют не только производить анализ, но и решать задачи синтеза – создание электропривода колебательного движения, обеспечивающего при требуемых выходных параметрах максимальную выходную мощность.

• 3.    Результаты расчетов и экспериментальных данных показали, что при прочих равных условиях режим работы МДП характеризуется более высокими энергетическими показателями благодаря обеспечению свободного энергообмена между фазами ротора, статора и источниками питания.

за счет фазовой модуляции питающих напряжений, целесообразно проводить по интегральным выражениям приближенно, либо для конкретного заданного интервала времени.