К вопросу об особенностях механизмов упрочнения в металлической матричной композиции

Введение. Известно, что физико-механические свойства алмазных порошков определяются большей удельной поверхностью и дисперсностью зерен. В частности, это демонстрирует уравнение Холла — Петча, которое выполняется в широком диапазоне размера зерен (вплоть до 1 мкм). Функциональные свойства указанных материалов обусловлены масштабным структурным фактором, поскольку он влияет на формирование структурно-чувствительных механических свойств — пределов прочности и текучести [1, 2]. Учитывая качественную корреляцию между пределом текучести и твердостью, можно прогнозировать повышение твердости, в том числе высокотвердых материалов: чем мельче наполнитель, тем меньше в нем дефектов — и, соответственно, выше прочность.

Материалы и методы. Механизмы упрочнения в высокотвердых материалах зависят от характера взаимодействия введенных частиц или волокон упрочнителя с материалом матрицы. Успешное применение эффекта дисперсного упрочнения показано в [3-6, 7]. При таком упрочнении в материалах создается структура, затрудняющая движение дислокации. Особенно сильно передвижение дислокаций тормозят дискретные частицы второй фазы, характеризующиеся высокой прочностью и температурой плавления. С учетом двухфазной структуры и высокой твердости получаемых материалов следует ожидать, что их износостойкость также будет выше, чем у неупрочненных материалов матрицы. Кроме того, для износостойкости композитов важным фактором является прочность границы раздела компонентов. Прочная адгезионная связь на границе раздела обеспечивает получение композита с большой жесткостью и более высокой статической прочностью [3, 6-8].

Согласно механизму, описанному Орованом, распределенные в объеме связки ультрадисперсные частицы алмаза влияют на деформационное упрочнение композиционного материала. Введенные в матрицу частицы дисперсного наполнителя тормозят движение дислокаций в металле, увеличивая его прочность при нормальной и повышенных температурах. К тому же они представляют собой механическое препятствие на пути распространения трещины, которая может появиться в матрице, и повышают сопротивление разрушению композиционного материала.

Еще одной характеристикой, определяющей связь армирующего наполнителя и матрицы, является температурный коэффициент линейного расширения. Для твердых веществ при постоянных давлении и температуре критерием термодинамического равновесия является минимум потенциала (или энергии) Гиббса. Эта величина показывает изменение энергии в ходе химической реакции и демонстрирует возможность протекания химических реакций между компонентами материала [5]. Таким образом, минимум изменения энергии Гиббса соответствует устойчивому равновесию между компонентами системы (табл. 1).

Таблица 1

Физические характеристики основных типов наполнителей [9, 10, 11]

Вещество и состояние	ΔGo обр., 298,15, кДж/моль	Микротвердость, *10 2 Мпа	Температурная устойчивость, °C
	Изменение энергии Гиббса
С (алмаз)	2,377	1000	650-700
W	0	258	3300-3400
Al 2 O 3	-1582,3	180-220	1500-1700
BN	-226,8	800-900	1100-1300
SiC	-60	300-320	1200-1300
BeO	-579,9	152	2500
Be 2 C	-948	780	2150

Из таблицы видно, что оптимальный наполнитель — алмаз. У него достаточно низкое значение изменения энергии Гиббса, самое большое значение микротвердости, но наименьшая температурная устойчивость. Алмаз обладает большой адсорбционной способностью [12] и наименее химически активен в сравнении с другими формами углерода. Названные качества являются важными преимуществами при использовании алмаза в качестве упрочнителя.

Цель работы — исследование особенностей механизмов формирования структуры металломатричной композиции.

Объекты исследования. В работе использовали стандартную связку — оловянистую бронзу M2-01 (20 мас. % олова, 80 % меди). В нее добавляли ультрадисперсный природный алмаз (УДПА, 0,5–4 мас. %), а также порошки (фракции 3/2 мкм, 7/5 мкм, –40 мкм).

Методика проведения исследований. Порошки природного алмаза (ППА, фракции 3/2 мкм, 7/5 мкм, –40 мкм) и субмикропорошок УДПА получены при переработке алмазов на предприятии ОАО «Сахадаймонд». Порошки изготавливались при оптимальных режимах на дробильно-классификационном оборудовании и вибростолах. На рис. 1 показаны стадии получения порошков. Снимки выполнены с помощью растровой электронной микроскопии (РЭМ).

а )

б )

Рис. 1. РЭМ-фотографии: мелкозернистого порошка от 7 мкм и менее ( а ); субмикропорошка ( б )

Для классификации алмазных порошков по зернистости применяли вибросита. Физические и механические характеристики изготовленных образцов испытывали по стандартным методикам. Для взвешивания использовали лабораторные электронные весы четвертого класса ВЛТЭ-500. Плотность ρ определяли микрометром МК 0–25 мм по ГОСТ 6507-78.

Результаты исследования. Твердость измерялась на приборе Equotip 3 фирмы Proceq по соответствующей методике ГОСТ. Предел пропорциональности при сжатии и модуль упругости определялись по ГОСТ 25.503-97. Результаты испытаний приведены в табл. 2.

Таблица 2

Влияние ППА на физико-механические свойства сплава М2-01

ПА, %	Пористость, %				Твердость, HВ				Предел пропорциональности при сжатии σ пр , МПа				Фактическая плотность ρ факт , кг/м3				Модуль упругости при сжатии Eс, МПа
A    5 ^ л у S о co О T £ =	0!		1		0!		1		0!		1		0!		1
0	41,0	41,0	41,0	41,0	41	41	41	41	9,7	9,7	9,7	9,7	7560	7560	7560	7560	5735,94
1	29,0	30,0	30,0	28,0	43	47	48	48	10,5	11,5	11,0	11,5	7630	7620	7610	7670	6771,03
2	27,0	28,0	28,0	26,0	43	43	51	53	10,5	11,5	12,0	12,5	7710	7700	7760	7750	6953,50
3	25,0	28,0	27,0	26,0	47	43	51	53	10,2	10,5	12,1	12,2	7730	7720	7770	7750	6580,27

Механика

Чтобы определить модуль упругости и предел пропорциональности, образцы сжимали на прессах до относительной деформации, равной 15–16%, при скорости нагружения 0,2 кН/с.

Пористость рассчитывали через фактическую и теоретическую плотности по формуле:

П = (1 - р / р т ) х 100%,

где р _т — теоретическая (расчетная) плотность беспористого материала; р — фактическая плотность исследуемого образца.

Теоретическую плотность получали по формуле:

р т = 100/( C 1 / р 1 + C 2 / р 2 + C з / р з + C 4 / р 4 ),                                      (2)

где C 1 , C ₂ , C ₃ и C ₄ — концентрации меди, олова, ППА и УДПА в порошковых смесях соответственно их плотности р 1 , р 2 , р з и р 4 .

В расчет приняты плотности:

• —    медь 8,96 х 103 кг/м³,

• —    олово 7,28 х 103 кг/м³,

• —    алмаз 3,5 х 103 кг/м³,

• —    УДПА 3,1 х 103 кг/м³.

Объем образцов вычислялся по формуле:

V = ( m 1 - m 2 ) / р ж ,                                                  (3)

где V — объем прессовки; m 1 — масса на воздухе; m ₂ — масса в воде; р ж — плотность жидкости.

В процессе исследования выяснилось, что с уменьшением размера фракции наполнителя наблюдается улучшение физико-механических свойств связки, модифицированной алмазным порошком.

Значения модуля упругости определялись для образцов с добавлением УДПА и чистой связки. Наилучшие показатели демонстрируют образцы с наполнителем из УДПА. В то же время рассматриваемые физико-механические свойства ухудшаются, если объем добавленных частиц УДПА превышает 2 %.

Металлографические исследования образцов позволили установить, каким образом частицы алмаза влияют на структуру матрицы. На рис. 2 представлены снимки микроструктур деформированных образцов.

Рис. 2. Снимки шлифованной поверхности деформированного образца с добавлением 2 % частиц алмазных порошков при увеличении х1000

На снимках четко различимы микроструктурные узкие и разветвленные объекты. Предположительно, это границы между зернами или микротрещины, образовавшиеся при деформировании.

Внутри зерен также присутствуют точечные микрообъекты, образующие дисперсную субструктуру. По сравнению с гранично-распределенными точечными объектами их плотность значительно меньше, но ощутимо больше, чем у исходной матрицы, в которой отсутствуют алмазные наполнители.

Основываясь на результатах металлографических исследований, можно утверждать, что при упрочне- нии материала матрицы действуют два механизма — дисперсный и зернограничный.

Если речь идет о дисперсном механизме, объем вводимого в материал матрицы порошка природного алмаза можно рассчитать по уравнению Орована [13]:

Z_N = 2Lk_Qln- ,

Ъ"    2 ПЛ 0 2Ь, где X — ближайшее расстояние между частицами; G — модуль сдвига матрицы; b — вектор Бюргерса; к0 — коэффициент, характеризующий тип взаимодействующих атомов с дислокацией.

Выбраны следующие значения: G = 0,367х10⁵ МПа для бронзы; b = 2,564 А для меди; коэффициент к ₀ равен 0,85.

Ближайшее среднее расстояние между частицами в зависимости от содержания и дисперсности рассчитано по формуле, предложенной в [14]:

^[(^Ч'.                  (5)

где L H — весовая доля наполнителя; d — диаметр или толщина частиц наполнителя.

В табл. 3 приведены расчеты среднего расстояния между частицами наполнителя в зависимости от их объема и размера.

Таблица 3

Ближайшее среднее расстояние между частицами наполнителя в зависимости от их объема и размера и упрочнение по уравнению Орована при введении частиц алмаза

Зернистость частиц	7/5			3/2			-40			УДПА
Содержание частиц, %	1	2	3	1	2	3	1	2	3	1	2	3
X, мкм	125.3	98.19	85.02	52.19	40.91	35.42	417.56	327.30	283.40	6.26	4.91	4.25
Z n , МПа	0.13	0.16	0.18	0.28	0.35	0.40	0.04	0.05	0.06	1.91	2.38	2.70

Расчетные данные были подставлены в уравнение Орована, и таким образом определено упрочнение за счет введения в материал матрицы частиц алмазных порошков.

Согласно расчетам. наибольшее упрочнение достигается при введении в матрицу УДПА, что в целом подтверждается экспериментальными данными.

При изменении геометрии зерна за счет агломерации частиц наполнителей на границах раздела в материале целесообразно рассчитывать изменение свойств материала согласно теории зернограничного упрочнения [15. 16].

Для определения количественного увеличения прочности материала при добавлении частиц алмазных порошков за счет зернограничного упрочнения были проведены расчеты по эмпирическому соотношению Холла — Петча [17]:

Да т = Мз-^1/2 .                                           (6)

где к —коэффициент Холла — Петча для данного материала; d ₃ — размер зерна.

Для расчетов использовались образцы, показывающие наибольшее увеличение прочности по теории Орована. Расчеты выполнены согласно данным. полученным по итогам обработки снимков микроструктуры поверхности. по методике. предложенной в [18].

Коэффициент Холла — Петча применен к меди. Согласно [19] он является величиной переменной, зависит от среднего размера зерна и варьируется в пределах 0,01-0.24 Мпа х м1/2. Расчеты показали. что наибольшее упрочнение дает введение в материал матрицы порошков ультрадисперсного природного алмаза. В целом, это подтверждается экспериментальными данными.

Средний размер зерна рассчитан согласно металлографическим исследованиям поверхности образцов:

4(^)

»з =           .                                                   (7)

где S _общ — общая площадь объектов; N общ — количество объектов.

При значении среднего размера зерен порядка 10-1 мкм коэффициент Холла — Петча равен примерно 0.01 Мпа х м1/2.

Расчеты по соотношению Холла — Петча свидетельствуют об увеличении предела текучести материала при добавлении частиц порошков природного алмаза. Предел текучести достигает максимального расчетного значения при содержании наполнителей 1 % (рис. 3).

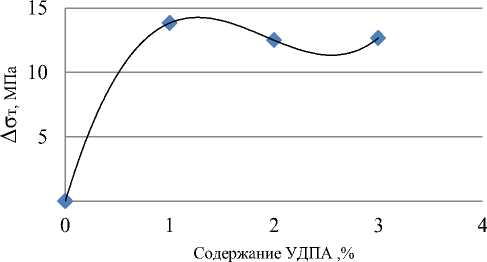
Рис. 3. Зависимость предела текучести от содержания УДПА

Механика

Обсуждение и заключения. Расчеты показали, что у образцов с добавлением порошков природных алмазов размер зерен меньше по сравнению с исходными. Этот факт можно объяснить следующим образом. Частицы алмаза, оседая на границах зерен материала, способствуют уменьшению их среднего размера. В результате меняется геометрия границ между зернами, образуются барьеры для дислокаций, и, как следствие, усиливается потенциальная способность материала сопротивляться пластической деформации. Предел текучести увеличивается примерно на 12–13 МПа, что коррелирует с расчетными данными, полученными при использовании теории Орована для дисперсионного упрочнения. Если речь идет о поликристаллическом материале, то, в принципе, предел текучести увеличивается при уменьшении размеров зерен. Добавленные в объем матрицы частицы алмаза увеличивая предел текучести, т. к. меняют геометрию зерен, уменьшая их среднюю площадь и размер.

Расчетные данные отличаются от экспериментальных, т. к. показывают увеличение упрочнения материала пропорционально количеству вводимых в объем частиц алмаза. Можно предположить, что модель упрочнения Орована не учитывает образование углерода и агломерацию алмазов в более крупные объекты в объеме матрицы при повышении количества вводимых алмазов.

Уменьшение количества пор при добавлении частиц УДПА в количестве 1–2 % можно объяснить высокими сорбционными свойствами наполнителя. При спекании компактов, полученных методом порошковой металлургии, частицы УДПА абсорбируют кислород, содержащийся в порошковой смеси, с образованием газов-восстановителей СО и СО 2 . Эти газы разрушают окисную пленку, покрывающую частицы порошковой смеси, и препятствуют окислению при спекании, тем самым уменьшая общий объем газов в порошковой смеси. В то же время газы-восстановители ускоряют процесс спекания материала. Сочетание этих факторов в итоге уменьшает остаточную пористость в материале, что подтверждается и расчетными данными. Если же объем частиц УДПА достигает 3 %, происходит увеличение содержания углерода в материале. В результате частицы наполнителя полностью не окисляются, тем самым увеличивая количество пор в материале.