К вопросу об устойчивости деревянных стержней при различных стадиях деформирования

Наша страна издавна богата запасами древесины, однако, применение деревянных конструкций в строительстве не так распространено по сравнению с привычными железобетонными или стальными. Одной из причин малого использования деревянных конструкций является недостаточный уровень проведенных исследований (особенно экспериментальных). В данной работе выполнено исследование устойчивости деревянных стержней на примере однопролетной деревянной плоской рамы.

Исследованием устойчивости деревянных стержней занимались многие деятели науки, например, Константин Пантелеевич Пятикрестовкий и Х. С. Хунагов. Так, в своей статье «Нелинейные деформации статически неопределимых деревянных конструкций» [1] они рассматривают статически неопределимые деревянные конструкции при несимметричных нагрузках. Авторы считают, что перераспределение усилий позволяет получить экономию материалов и обеспечить безопасность сооружений.

В данной работе применяется метод, разработанный советским учёным А. Р. Ржанициным. Известно, что сжатые, а также сжато-изогнутые деревянные элементы деформируются нелинейно, что приводит к усложнению ряда расчетов. Диаграммы деформирования древесины, полученные в результате многочисленных экспериментов, дают возможность описать процесс деформирования рядом уравнений. Так, метод, предложенный Ржанициным позволяет учитывать сложность процесса деформирования древесины во времени с помощью разбиения процессов деформирования на три стадии и замены сложной нелинейной связи между напряжениями и деформациями кусочно-линейными зависимостями, то есть прямыми (рис. 1), удовлетворяющими условию неразрывности деформаций, напряжений и скоростей деформирования при переходе от одной стадии деформирования к другой [2].

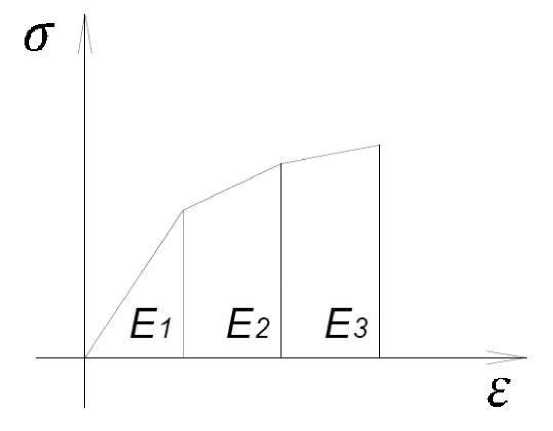
Рисунок – 1. График разбиения процесса деформирования на три стадии

Для древесины данные стадии характеризуются следующими особенностями:

• 1)    в первой стадии деформирования ползучесть является обратимой, подчиняется основным положениям линейной теории ползучести (закону Гука);

• 2)    во второй стадии – установившейся ползучести – деформирование идет с постоянной скоростью нарастания деформаций ползучести (при постоянных нагрузках), деформации здесь большей частью необратимы;

• 3)    в третьей стадии имеет место критическое нарастание необратимых деформаций во времени [2].

В данной работе рассмотрены первая (случай 1) и вторая (случай 2) стадии деформирования на примере деревянной рамы. Расчетная схема рамы представлена на рисунке 2. Сечение стержней b х h = 0,4 х 0,4 м.

Р=3 мн

Р.=4 МН

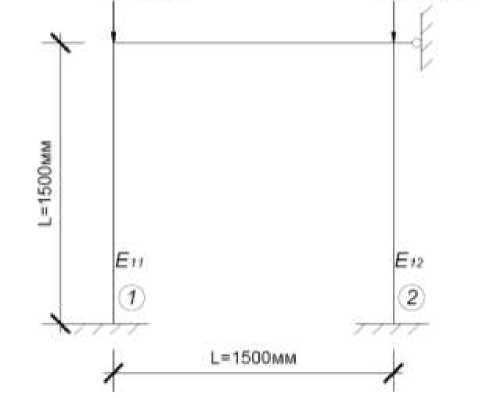
Рисунок - 2. Расчетная схема

Для первого случая характерно равенство модулей деформаций в первой и второй стойках. Обозначим модули деформаций как: Е_и = Е₁₂ = Е и проверим равенство модулей деформаций по формуле (1) [1]:

Едл (to, t) = [«(‘0><*+»£-‘^ + ^ ^1 (1 + b(t — (о)0-21)]"', где     (1)

v (L)                    OIL)

Для первой стадии деформирования в первой стойке:

= 0

( = (1 = 100 сут

10"210

^b = 0,735 — 0,02086W = 0,735 - 0,02086 x 12 = ^0,0048468

W = 12% — влажность древесины, %

Pi3

a(t)i = j = — = 18,750 МПа а,    18,750

£(t o ) i =71 = 77-773 = 0,0015625

Е;   1210

E11(t0,t) = 0,169 • 103 МПа

Для первой стадии деформирования во второй стойке:

Pi 4

a(t)i = — = —— = 25 МПа

v J1 Л   0,16

а     25

£((о)1=е;=127103 = 0,00208

E12(t0,t) = 0,169-103 Мпа

Таким образом, как предполагалось, модули деформаций в первой и второй стойках оказались равны друг другу.

Для расчета рамы на устойчивость используем классический метод строительной механики – метод перемещений.

• 1.    Записываем уравнение устойчивости

• 2.    Находим коэффициенты векового уравнения методом итераций для

(^Н^^^+^М    (2)

<^2(^1) = -1 ИЛИ Ч^Ы = —1

первой и второй стоек:

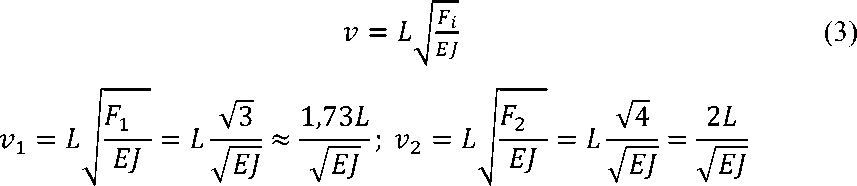
12 = 1,15611

4,6587

11 = 4,6587 или 11 = ——— = 4,0300173 1,156

12 = 1,156 • 4,6587 = 5,3854572 или 12 = 1,156 • 4,0300173 = 4,6587

Тогда коэффициенты приведенной длины равны:

лл

111 = „     = 0,674 или 11 = —— —— = 0,77915

• ¹  4,6587   ,       ^м 4,0300173

лл

11? = „         = 0,583 или и? = ———— = 0,674

• 2   5,3854572    ,         2   4,6587,

Приведенная длина L₀ ^ равна:

L01 = L11 = 1,5 • 0,674 = 1,011 или L01 = L11 = 1,5 • 0,77915 = 1,16873

L02 = L[2 = 1,5 • 0,583 = 0,8745 или L02 = L[2 = 1,5 • 0,674 = 1,011 Уточняем критическую силу по формуле Эйлера:

FKP =     • EJ = „3;147 • 0,169 • 103 • 04- = 3,48 кН или кр 1   L012        1,0112                 12

F =  J'14   • 0,169 • 103 • 0^4- = 2,6 кН кр1   1,168732

Fkd =     • EJ = т-314^ • 0,169 • 103 • °4- = 4,65 кН или кр2   ^022        0,8745 212

F = З'14 2 • 0,169 • 103 • 0^4- = 3,48 кН кр 2   1,011 212

Для второго случая E21 ^ E22 определяем модули деформаций по формуле (4) [1]:

к1—

E d- <^ = [^ ₊ ^ (t-t^^-ti] , где (4)

Для второй стадии деформирования в первой стойке: t = t 1 = t_t = 100 сут

Н = 0,75E₀ = 0,75 • 12 • 10³ = 9000 МПа

a(t) = 18,75 МПа вдл = 22 МПа

E₂₁(t₀,t) = 7670,45 МПа

Для второй стадии деформирования во второй стойке:

• МПа

  E₂₂(t₀,t) = 10227,27 МПа

• 1.    Записываем уравнение устойчивости

• 2.    Находим коэффициенты векового уравнения методом итераций для первой и второй стоек:

С^- ^^ ^₂(V 1 ) + ^ •           + ^ - ( 2^ )² = 0   (5)

Выдвигаем гипотезу, что E₃ = E₀ = 12 • 10³ МПа , тогда

(7,6705 х 10 3 ^ 2 (^ 1 ) + 12 • 10³) • (10,2273<р₂(п₂) + 12 • 10³) = 36 х 10⁶

vi = L l^ = / ^V3     Ху « 0,0197764у

^E 21 ^J 77,6705 х 10^{3 J              J}

v2 = L I— = ,    V4  --x - « 0,019776503

7 E22J  710,2273 x 103 J               J

Принимаем 1 1 = v₂, тогда

(7,6705 x 103^2(171) + 12 • 103) • (10,2273^2(171) + 12 • 103) = 36 x 106 Решаем квадратное уравнение:

%1 = ^2(171) = -2,07396; 171 = 12 = 5,6754 jq =

Тогда коэффициенты приведенной длины и приведенная длина для каждой стойки соответственно равны:

/ = / = —— = 0,5533; Lo1 = -02 = -/ = 1,5 • 0,5533 = 0,82995 м

5,6753

/ = / = —^— = 0,6115; Lo1 = L02 = -/ = 1,5 • 0,6115 = 0,91725 м

5,135164

Уточняем критическую силу по формуле Эйлера:

F = ^ •EJ =  314QZ2 • 7670,45 • 0,4- = 234,2 кН

кр1   -012       0,829952             12

Fkd =     • Е/ =  ^^^t^^ • 10227,27 • °4- = 255,68 кН

кр2   -022        0,917252          ,     12        ,

Вывод: во втором случае значение критической силы оказалось значительно больше, а приведенная длина меньше по сравнению с первым случаем. Данный анализ говорит о том, что в первой стадии деформирования стержни теряют устойчивость при тех же самых значениях сосредоточенных нагрузок значительно раньше.