К вопросу об устойчивости различных стационарных точек в задаче о малых колебаниях аэродинамического маятника в потоке среды

В задачах динамики тел, на которые воздействуют аэродинамические силы, существует проблема моделирования стационарных режимов и исследования их устойчивости при движении тел различного вида в атмосфере. Существует также проблема демпфирования автоколебаний, появляющихся в результате возникновения флаттера при движении в сопротивляющейся среде. Флаттер – это форма потери устойчивости, связанная с возрастающими автоколебаниями крыла при воздействии аэродинамических сил, иногда ведущая к разрушению конструкции. Простейшие механические системы в этой области – это

К вопросу об устойчивости различных стационарных точек в задаче о малых колебаниях ...

Беляков Дмитрий Валерьевич кандидат технических наук, доцент кафедры математики, Московский авиационный институт (Национальный исследовательский университет), Москва. Сфера научных интересов: динамика движения в атмосфере, устойчивость, управление движением. Автор 30 опубликованных научных работ. ORCID: 0000-0001-5093-2963, SPIN-код: 3427-0812, AuthorID: 851172.

крыло, парус, парашют, несущий винт с вертикальной осью, аэродинамический маятник в потоке среды. Такие задачи и в настоящее время очень актуальны в авиаракетостроении.

В работе рассматривается движение аэродинамического маятника в потоке среды. Исследуется нарушение единственности решений, что редко встречается в физических задачах, и строятся области устойчивости с помощью метода Раусса – Гурвица.

Постановка задачи

Рассматривается задача о теле, представляющем аэродинамический маятниик, состоящий из стержня длиной r и аэродинамического профиля, развернутого ортогонально стержню [1–3]. Тело закреплено в центре масс с помощью обычной и спиральной пружины и совершает автоколебания в потоке среды (см. Рисунок 1).

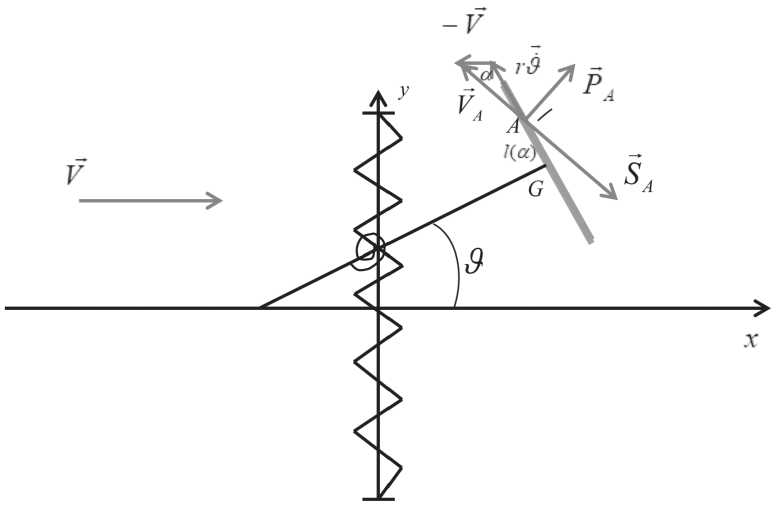
Рисунок 1. Колебания аэродинамического маятника в потоке среды

Cила упругости и возвращающий момент имеют вид F =- kx , M = - c θ . Будем считать, что центр давления пластинки, точку А , к которому прикл адываются силы воздействия среды, подвижен относительно профиля. Абсолютные величины аэродинамических сил, которые воздействуют на профиль, являются экспериментальными данными и приводятся в [4, с. 154]:

| 5 A | = s( a )V A = 0,5 po c x (a^VA,

| ^A |= p(a)VA = 0,5POCy («)VA- где a - угол атаки между вектором V?A и пластинкой; cx, cy - безразмерные аэродинамические функции; ρ – плотность воздуха; σ – площадь одной пластинки.

Позиционные координаты необходимо выбрать как координату центра масс тела и угол ϑ отклонения пластинки от горизонтали. Тогда уравнения движения тела будут иметь вид

I

I

I

I

my = s ( a ) V A (1 ( a ) 9 sin 9 - r 9 cos 9 - у ) - p( a )V A ( r 9 sin 9 + 1( a^9 cos У + V ) - ky ,

J 9 = rV2T(a) -1 (a) VA n(a) - c9, где

τ(α) = p(α)sinα- s(α)cosα, n(α) = p(α)cosα+ s(α)sinα есть аэродинамические функции нормальной и касательной сил соответственно.

Кинематические соотношения, связывающие V A , a с y , y, 9 , 9 , приведены в формулах

V A sin a = 1 ( a ) 9 - y sin 9 + V cos 9 ,

V A cos a = r 9 + y cos 9 + V sin 9 .

Сделаем переход к следующим безразмерным переменным:

Y = ^y ; т = Vt ; Q = b ⁹ U = V A ; M = bb V V

mb к = kb c = c

0,5 ρσ    0,5 ρσ V ²    0,5 ρσ V ²

J            l ( α )      r

I =        ε ( α ) =     R =

0,5 ρσ b    bb

Тогда система (1) запишется как

MY = c x ( a ) U ( R ^ cos 9 + ^s ( a )sin 9 - Y ) + c_y ( a ) U ( R Q sin 9 +Q f ( a )cos 9 + 1) - KY , l 9 = U ² ( Rc _T ( a ) - e ( a )c n ( a ) ) - C 9 .

Алгебраические соотношения (2) преобразуются к виду

U sin a = f ( a ) Q - Y sin 9 + cos 9 ,

U cos a = R Q + Y cos 9 + sin 9 .

Математическая модель колебаний аэродинамического маятника в безразмерном виде запишется как (3), (4).

Геометрический анализ подпространства фазовых переменных

При численном интегрировании системы (3) необходимо определить угол атаки из кинематических соотношений (4). При этом происходит нарушение однозначности решения при определении угла атаки при некоторых значениях . Аналогичная задача с не-

К вопросу об устойчивости различных стационарных точек в задаче о малых колебаниях ...

подвижным центром давления рассматривалась в [5, c. 38]. В процессе численного интегрирования уравнений движения определение угла атаки на каждом шаге сводится к решению нелинейного уравнения (5) при различных значениях фазовых переменных S , Q , Y :

( R Q + Y cos S + sin S ) tg a - Y cos S - sin S = f ( a ) Q                        (5)

Входящие в правую часть рассматриваемого уравнения tg a , s ( a ) п периодичны, это значит, что если a = a ( S , Q ) является решением уравнения (5), то и a = a ( S , Q ) + п к также является его решением. Проанализируем коэффициенты в уравнении (5). Знак выражения R Q + Y cos S + sin S отвечает за направление ветвей у тангенса. Свободный член - Y cos S - sin S производит смещение тангенса вверх или вниз. Знак Q влияет на расположение и ширину правой части уравнения (5). В зависимости от значений S , Q , Y уравнение (5) может либо вообще не иметь решений, либо иметь от одного до трех решений. Попытаемся оценить размеры границ для областей неоднозначности и изобразить эти области в пространстве S , Q , Y .

Нелинейной системе двух уравнений, заданной в параметрической форме, удовлетворяет любая точка ( S , Q ), лежащая на этой области при Y = const :

[ ( R Q + Y cos S + sin S ) tg a - Y cos S - sin S = s ( a ) Q ,

• 1    R Q + Y cos S + sin S                                             ⁽⁶⁾

I----------2--------= £\a ) Q .

I cos a

Чтобы построить огибающие к каждой поверхности, нужно найти точки возврата, в которых искомая поверхность приходит к однозначному виду. Есть несколько способов нахождения точек возврата, но необходимо остановиться на одном из них, который подробно приведен в статье [4]. После нахождения точки возврата, решая систему нелинейных уравнений (6), нужно найти переменные S , Q . В результате можно получить огибающие и нанести их на плоскость S , Q .

Проведем анализ числа решений на плоскости S , Q и в подпространстве фазовых переменных S , Q , Y .

• I.    Рассмотрим случай S >  0 , Q >  0 , Y >  0 , S <  0 , Q< 0 , Y >  0 , изображенныйм на Рисунке 2 в виде двух плоских областей, напоминающих трехконечные звезды при Y = 9 . Внутри них нелинейное уравнение (5) имеет почти везде по три решения на периоде п . Если находиться вне найденных фигур, то нелинейное уравнение (5) почти везде имеет только одно решение. Красной линией изображена кривая R Q + Y cos S + sin S = 0 нулевого уровня тангенса, которая делит полученные области на четыре части. Кроме того, линия R Q + Y cos S + sin S = 0 на любом уровне Y является касательной к огибающим в крайних точках возврата. Точность проводимых вычислений в данной статье позволяет проводить в большей степени качественное исследование.

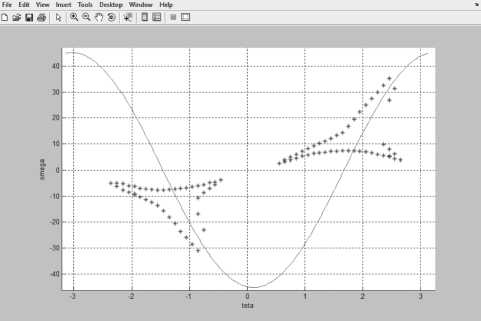
Рисунок 2. Огибающие в случаях Э >  0 , О >  0 , Y >  0, Э <  0 , О< 0 , Y >  0 при с = 0.5, b = 0.25, R = 0.2, Y = 9

Проведем сечение области неоднозначности в простейшем случае без пересечения линии R Q + Y cos Э + sin Э = 0 Оно будет представлять из себя одинарную складку, изображенную на Рисунке 3. Прохождение неоднозначности в этом случае происходит без нарушения непрерывности угла атаки.

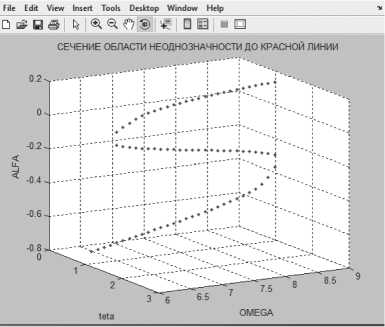
Рисунок 3. Сечение области неоднозначности без пересечения линии нулевого уровня тангенса R О + Y cos Э + sin Э = 0 при некотором Э

Проведем графическую интерпретацию непрерывного параметрического перехода через линию R О + Y cos Э + sin Э = 0 при решении нелинейного уравнения (5). Возьмем некоторое значение Э . Будем изображать самое левое решение уравнения (5) в виде некоторой кривой на плоскости Э , О снизу вверх от начала правой фигуры, увеличивая О с некоторым шагом (см. Рисунок 4).

К вопросу об устойчивости различных стационарных точек в задаче о малых колебаниях ...

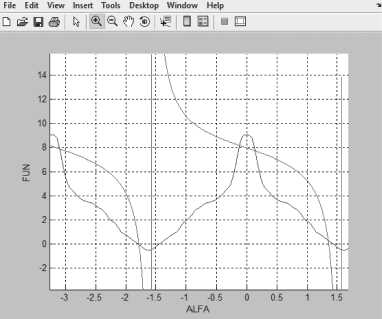
Рисунок 4. Решение нелинейного уравнения при 3 = 2.05355, Q >  0

R Q + Ycos 3 + sin 3 < 0 при ст = 0.5, b = 0.25, R = 0.2, Y = 9

При увеличении Q значение R Q + Y cos 3 + sin 3 увеличивается и приближается к нулю.

Ветви тангенса и решение (5) становятся ближе к асимптоте а = -^П (см. Рисунок 5).

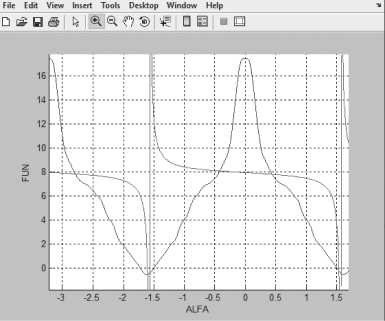
Рисунок 5. Решение нелинейного уравнения при 3 = 2.05355, Q >  0 R Q + Y cos 3 + sin 3 < 0 при ст = 0.5, b = 0.25, R = 0.2, Y = 9

При выполнении равенства R Q + Y cos 3 + sin 3 = 0 тангенс вырождается в прямую на Рисунке 6 и в этом случае (5) имеет уже два решения.

После перехода через нулевой уровень выражение R Q + Y cos 3 + sin 3 принимает уже положительные значения, у ветви тангенса меняется направление, и можно двигаться уже правее а = - ^П (см. Рисунок 7).

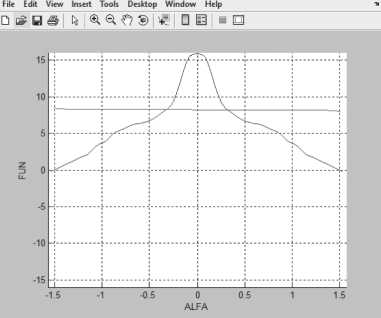
Рисунок 6. Решение нелинейного уравнения при 5 = 2.05355, О >  0

■                                                                                                                                                                   <

R Q + Y cos 5 + sin 5 = 0 при с т = 0.5, b = 0.25, R = 0.2, Y = 9

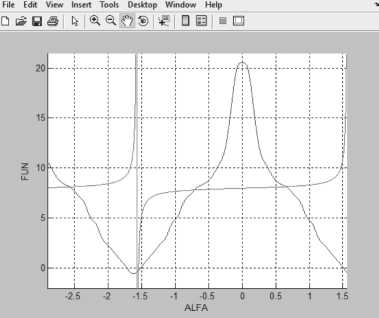
Рисунок 7. Решение нелинейного уравнения при 5 = 2.05355, О >  0

R Q + Y cos 5 + sin 5 > 0 при с = 0.5, b = 0.25, R = 0.2, Y = 9

Далее два соседних решения сближаются, и можно перейти на среднюю ветвь поверхности неоднозначности (см. Рисунок 8).

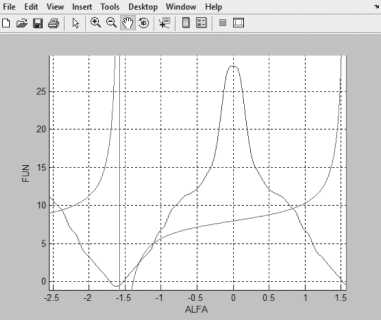
Рисунок 8. Решение нелинейного уравнения при 5 = 2.05355, 0 >  0 R О + Y cos 5 + sin 5 >  0 ■

при с = 0.5, b = 0.25, R = 0.2, Y = 9

К вопросу об устойчивости различных стационарных точек в задаче о малых колебаниях ...

Далее движемся обратно и уменьшаем Q . Пройдя весь отрезок неоднозначности, можно перейти на верхнюю ветвь сечения и снова пройти отрезок вперед (см. Рисунок 9).

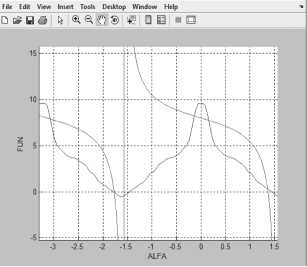
Рисунок9. Случай S> 0, Q> 0, R Q + Ycos S + sin S > 0

I при ст = 0.5,b = 0.25, R = 0.2, Y = 9

Одно из сечений области неоднозначности при пересечении линии нулевого уровня R Q + Ycos S + sin S = 0 изображено на Рисунке 10. Таким образом, при параметрическом переходе через красную линию нулевого значения тангенса решение а = a ( S , Q ) меняется непрерывно, и гладкость поверхности неоднозначности сохраняется.

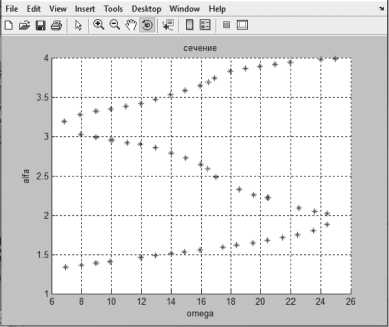
Рисунок 10. Сечение области неоднозначности с учетом пересечения линии нулевого уровня R Q + Y cos S + sin S = 0 при S = 2.05355, Q> 0

Если точка находится на кривой R Q + Y cos S + sin S = 0 сверху от левой части Рисунка 2, то уравнение (5) не имеет решений. В точке касания кривой R Q + Y cos S + sin S = 0 и верхней огибающей уравнение (5) имеет одно решение. В случае если точка находится под кривой R Q + Y cos S + sin S = 0 снизу от левой части Рисунка 2, уравнение (5) имеет два решения. Аналогично точка ведет себя при S >  0, Q >  0 .

• II.    Рассмотрим случаи, когда S> 0, Q< 0, Y > 0 или S < 0, Q> 0, Y > 0 .

Если S , Q имеют разные знаки и Y > 0 , то уравнение (5) всегда имеет только одно решение.

• III.    Рассмотрим случаи, когда S> 0, Q< 0, Y <  0 или S <  0, Q> 0, Y <  0 . Сделаем в нелинейном уравнении (5) замену переменных переменных Y 1 =- Y, S 1 = -S, Q 1 =-Q , и после несложных преобразований можно показать, что уравнение не изменилось:

( R Q 1 + Y 1 cos S 1 + sin S 1 ) tg a - Y 1 cos S 1 - sin S 1 = f ( a ) Q 1

Таким образом, случай, рассмотренный при Y >  0 для однознаковых значений S , Q , изображенный на Рисунках 2, 3-8, эквивалентен случаю Y <  0 , построенному для разнознаковых параметров S , Q , изображенному на Рисунке 11. Красной линией изображена кривая R Q+ Y cos S + sin S = 0 , которая делит полученные области на четыре части. Внутри этих областей нелинейное уравнение (5) имеет почти везде три решения. Графическая интерпретация решений полностью аналогична изображенной на Рисунках 3–8, поэтому ее приводить не нужно.

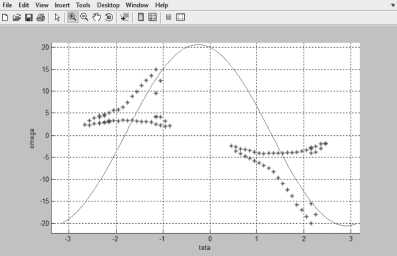
Рисунок 11. Огибающие в случаях S >  0, Q< 0 и S < 0, Q> 0 при ст = 0.5, b = 0.25, R = 0.2, Y = - 4 и Y = - 5

На Рисунках 12, 13 изображены две области в пространстве S , Q , Y для равнознаковых значений параметров S >  0, Q> 0 или 9< 0, Q< 0 при 1 <  Y <  9 . Внутри этих многообразий нелинейное уравнение (5) имеет три решения. В обоих случаях области при уменьшении абсолютного значения Y уменьшаются и смещаются правее, примыкая к нулевому уровню Y = 0 .

Аналогично исследуются две области для разнознаковых значений параметров S< 0, Q> 0, Y < 0 , S> 0, Q< 0, Y < 0 , изображенные на Рисунке 14, получается очень похожая картина.

На Рисунке 15 изображены огибающие на линии нулевого уровня при Y = 0 . Они сместились вправо, уменьшились, вытянулись и совсем невелики по сравнению с верхними сечениями. Левая нижняя фигура пересекает ось ординат и содержит не только однознаковые, но и разнознаковые значения параметров S , Q . Внутри фигур, как и в рассмотренных выше случаях, происходит смена знака коэффициента при тангенсе.

К вопросу об устойчивости различных стационарных точек в задаче о малых колебаниях ...

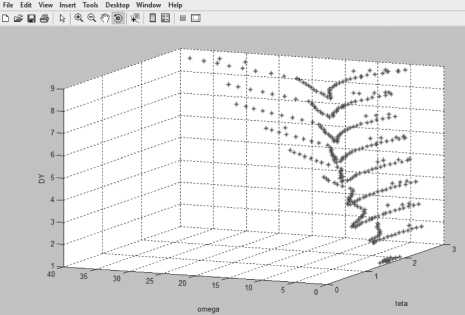
Рисунок 12. Линии уровней для областей неоднозначности в случае 1 <  У <  9 для однознаковых значений параметров Э >  0 , Q> 0

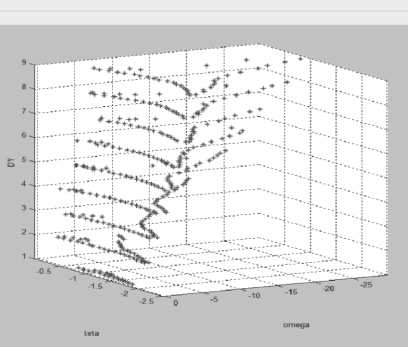
Рисунок 13. Линии уровней для областей неоднозначности в случае 1 <  У <  9 для однознаковых значений параметров Э <  0, Q< 0

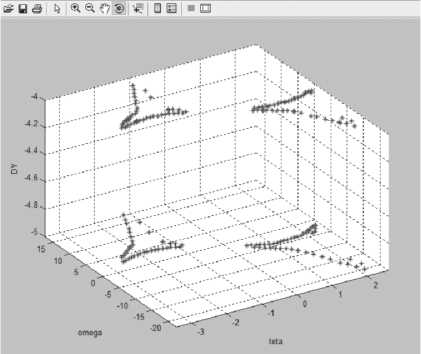
Рисунок 14. Линии уровней для областей неоднозначности в случаях - 5 <  У <- 4 для разнознаковых значений параметров Э <  0, Q> 0, Э >  0, Q< 0

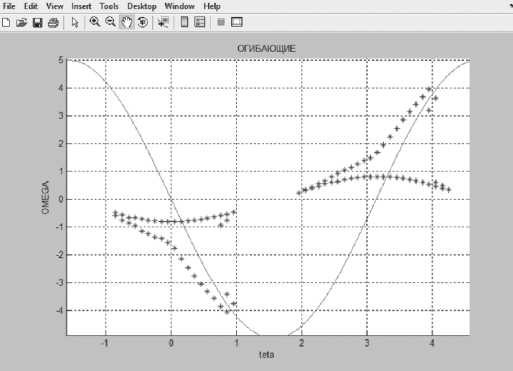
Рисунок 15. Огибающие в случае линии нулевого уровня Y = 0 для значений параметров < 9 , Q

Смоделируем ситуацию, когда фазовая траектория входит в область неоднозначности. Каким образом будет вести себя численное решение? Как исключить ошибки? С помощью какого алгоритма можно сохранить непрерывность угла атаки при нахождении численного решения в области неоднозначности?

Необходимо перейти к следующему этапу работы нахождению стационарных точек и исследованию их устойчивости.

Исследование стационарных точек и их устойчивость

Пусть тело движется поступательно. В этом случае Y = 0, 0 = 0 из кинематических соотношений (4). Из 0 * = const , Y . = const , следует, что tg a * = ctg 0 * , откуда а * + 0 * = — .

Для нахождения стационарных решений запишем уравнения равновесия 2

C y ( а * ) - kY . = 0,

^

—

Rc _т ( а * ) - г ( а * ) c n ( а * ) = C (— - а * ).

Графическая интерпретация решений системы (7) приведена на Рисунке 16.

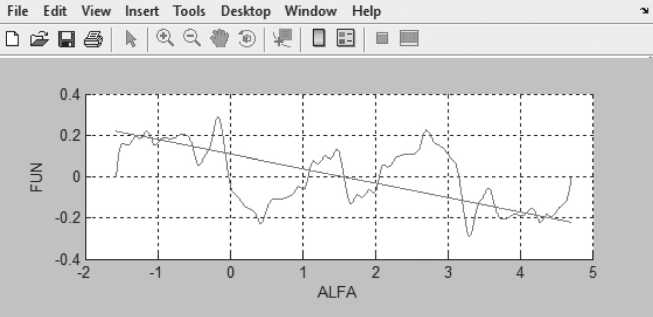
Рисунок 16 . Уравнения равновесия для нахождения стационарных точек

В статье [5] проведен подробный анализ найденных стационарных точек в различных случаях. Понятно, что безразмерный коэффициент жесткости C играет важную роль

К вопросу об устойчивости различных стационарных точек в задаче о малых колебаниях ...

в создании бифуркаций положений равновесия и количестве стационарных точек. В случае когда C = 0 , множество стационарных точек счетно.

В статье [3] показано, что найденные стационарные точки никогда не могут попасть в область неоднозначности и имеет смысл проводить исследование устойчивости в указанных точках. Предположим, что маятник совершает малые колебания около произвольной стационарной точки Y _*, ϑ _* . Пусть Y → Y _* и ϑ → ϑ _* . Введем малые отклонения: Y = Y _* +∆ Y , ϑ = ϑ _* +∆ ϑ .

Линеаризуем уравнения движения (3), (4), если ∆ Y → 0 и ∆ ϑ → 0 .

Для построения воспользуемся критерием Гурвица [7] для системы четвертого порядка. Условия Гурвица имеют вид a0 =MI >0, ai = Mg i + fi I > 0, a 2 = M(C-(s'(a* )cn (a*)) + s(a* )cn (a*)) )+f. g 1 +f2 g 2 +KI>0, a 3 = f1(C - (s'(a* )cn (a*)) + s(a* )cn ‘(a*))) + KI > 0, a 4 = K(C - (s' (a* )cn (a*)) + s(a* К' (a*)) )>0,

a1a3

∆ ₃ = a₀

a₂a₄ > 0.

a1

a 3 0

Здесь f i = f i ^{( a} * ) g i = g i ^{( a}« ) ^f 2 = ^f 2 ^{( a}« ) g 2 = g 2 ^{( a} *) — некоторые функции.

Области устойчивости для точек Y . , У * на плоскости безразмерных параметров ( C , I ) выделены зеленым цветом и изображены ниже на Рисунках 17–20.

На Рисунке 17 изображена область устойчивости для центральной стационарной точки, находящейся в состоянии покоя в случае Y → 0 , ϑ → 0 . При малых значениях безразмерного момента инерции на ней сразу возникают автоколебания. Границы областей устойчивости описываются прямой I = - ^g ⁱ C = ( S ( a * ) c_n ( a * )) + s ( a * ) c_n '( a * )) ) , которая способствует ветвлению положений равновесия. Условие для a ₃ представлено в виде синей прямой I =[M( (s' ( a * ) c n ( a * )) + s ( a * К'( a * )) - C ) - f _L g ₁ - f 2 g 2 ]/ K , и оно является самым слабым.

Таким образом, прослеживается тенденция увеличения области устойчивости по мере удаления от центральной стационарной точки, и в крайних точках область устойчивости вырастает достаточно сильно.

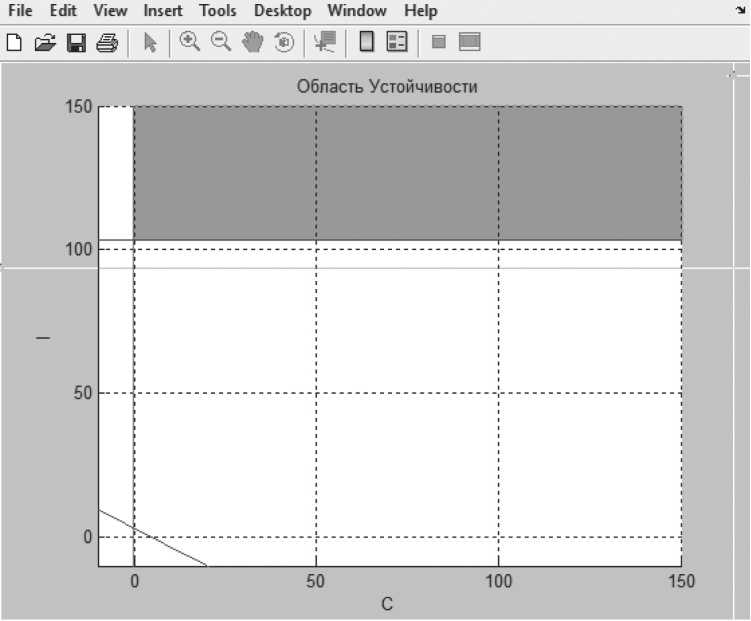
Рисунок 17. Область устойчивости – центральная точка при тета Θ = 0

File Edit View Insert Tools Desktop Window Help

D в: Й i | к | ® Q ♦ ® | * | □ 0 | я H

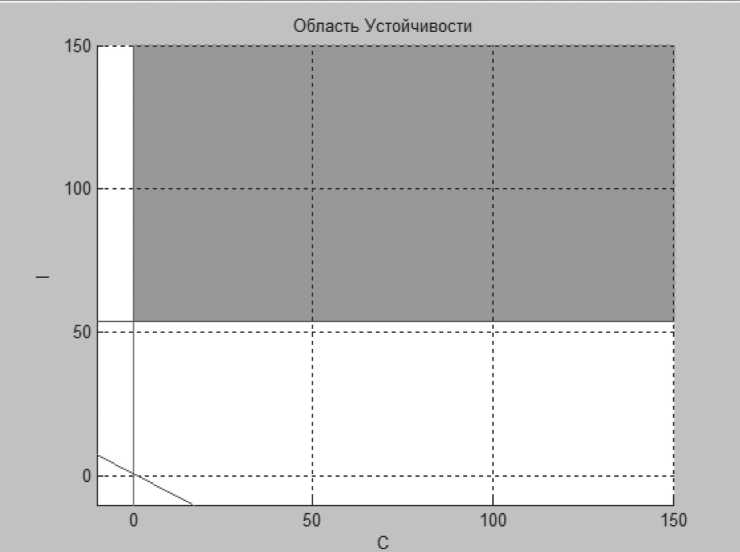
Рисунок 18. Область устойчивости при 4-й точке справа

К вопросу об устойчивости различных стационарных точек в задаче о малых колебаниях ...

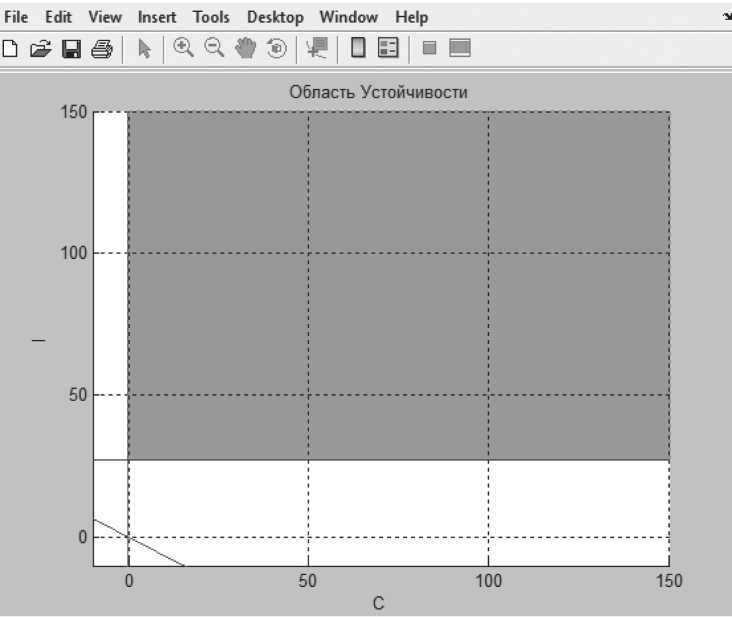
Рисунок 19 . Область устойчивости при 6-й точке справа

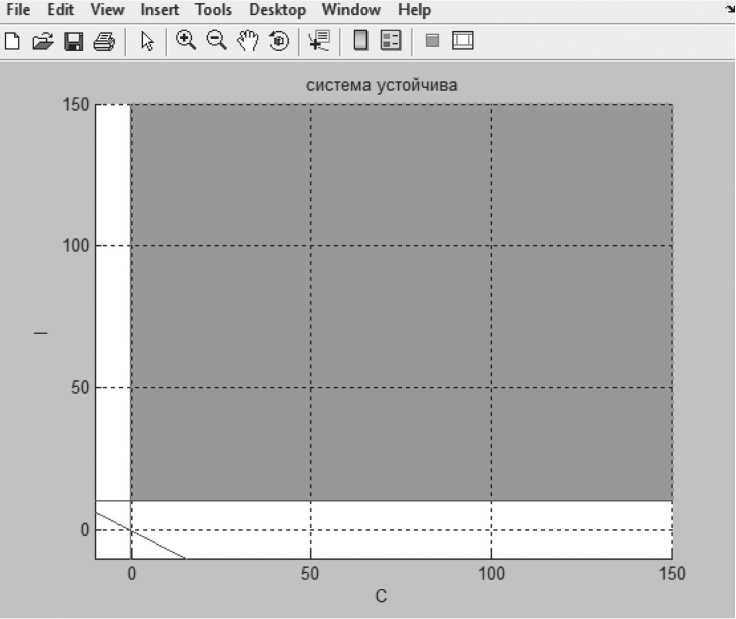
Рисунок 20. Область устойчивости – крайняя точка слева

Заключение

• 1.    Создана математическая модель колебаний аэродинамического маятника.

• 2.    Изображены огибаюшие и проведен параметрический анализ областей неоднозначности;

• 3.    Проведены исследования устойчивости, в которых реализован критерий Гурвица и изображена область устойчивости при различных значениях параметров C , I .

Аналогичные задачи также рассматривались в работах [7; 8].