К вопросу обтекания вогнутой поверхности потоком сжимаемой жидкости

Рассмотрим режим, соответствующий длинам волны вихрей Гертлера - Тейлора X, сравнимым с толщиной пограничного слоя δ. В этом случае характерные размеры возмущенной области течения совпадают по порядку величины, тогда одинаковые порядки будут иметь и возмущенные величины вертикальной и трансверсальной скоростей v~W, что следует из уравнения неразрывности и принципа минимального вырождения.

Предположим, что вихри вызывают нелинейные изменения основного течения, тогда

u~Au~0.

Нелинейность, проявляющаяся в трансверсальном направлении, дает

w~Aw~(Ap)2.                                                 (2)

При этом исследуются нелинейные процессы, проявляющиеся в течении с характерным масштабом в направлении координаты z, равным X, что определяет величину градиента давления в поперечном направлении:

dp ~ pu2 dy x '

Отсюда Др ~_£И. Далее v ~ w ~ е ? х ? .

Из уравнения неразрывности и оценок (1) - (3) можно найти продольный размер возмущенной области х ~ £? и?.

Для дальнейшего анализа важно оценить порядок отношения диффузионного и инерционного членов в уравнении продольного импульса d?u

Р dy2       1 1

—dU ~ ^{0(£2 и2)} ^ °- ^{p u}

Понятно, что в таких условиях не выполнено условие прилипания и поэтому необходимо ввести на дне основной области подслой с толщиной

3      1

у ~ £4 и~4, течение, в котором будет описываться системой уравнений трехмерного пограничного слоя.

Решение такой системы можно представить в виде

I

1     1

х * 1 + Хе-2х-2ха

У * ^У а

z * ^za

U(X, y,z,£) * Па(ха, ya,Z«) + ^

(      £) * (        ) Л-1г”х” +

W(X, y, Z, £) * Wa(xa, ya, Za) • £2X2 + •••

p(x,y,z.£)* pa(x«.y„.z«) + -

H(x,y. z. £) * На(ха, ya. za) + •

Pfyp,) 1 + £XPa(x«. ya,z«)+^.         .

Подстановка этих разложений в систему уравнений Навье - Стокса и совершение предельного перехода при Re → ∞, Ge → ∞ приводят к модифицированной системе уравнений Эйлера для трехмерного возмущенного течения:

d(p q U g ) ₊ d(p g V_a) ₊ d(p _a w_a) = ₀ dX a        dy_a       dZ a

8ua ,     8ua ,     8ua n ua 8xa + va jy; + "a JZ^ = 0

Hu,,^ + ^ + w_a J^ = ] + u ; + -J ^p i = 0

^{L a} 8 x ;     ^a 8y _a       ^a dz _a ^{J      a}    p_a 8y _a

α

α

r dwa ,    dwa ,     dwai ,

[u - ^ ^+v ^^+w ex ? ]⁺

1^ = 0

P _a ^8z a

dHa ,    дНа ,     дна   л ua -т+ + va -+ + wa --= = 0 a dxa     a dy a dza

£ 2

0 = ^

-

Отличие системы уравнений (6) от обычной системы уравнений Эйлера состоит в наличии члена в уравнении для поперечного импульса, учитывающего влияние центробежных сил.

Другая особенность связана с отсутствием градиента давления в уравнении продольного импульса. Из второго уравнения системы (6) следует сохранение продольной составляющей вектора скорости вдоль линии тока. Аналогичным первым интегралом обладает и уравнение для полной энтальпии. Для возмущений малой амплитуды решение системы уравнений (6) можно представить в виде

u(x) = u ₀ (y _a ) + TU a (y _a ) sinz _a exp (ax _a ) + -v a = ^Tv a (y _a ) ^exP ⁽«^x a ^)sinz « ⁺

W a = TW a (y _a ) exp («X _a )C0SZ _a +

Ha = Ho (ya)T Go(ya) exp (axa)sinza+ pa = r0 (у«) + T R«(y«) exp (ax«)sinz«+ Pa = Po (ya) + T Pa(ya) exp (axa)sinza+

T « 1.

Ограничиваясь нулевым и первым приближением из (6) и (7), можно получить систему обыкновенных дифференциальных уравнений вида apoua + auaRa + Р0^ + vaP0 - Powa = 0

aU o U a + V a U o = 0

• 1       R _a

e^[au o U a + 2u o U a ^] + —P « U o — -yPo = 0 ^p o          ^p o ^o

P‘ -u2

_P Q ^{P0 U0}

au0Wa + R^ = 0 p0

auoGa + VaHo = 0

H - Y^-1 , Ho

Ho   Pop" + 2

G« = - (1/ (^ - 1) P^ Ra/p° + uoua

9 / 2 9 A

Po = Po(uoP")Po = Povi(auo),

где

() = d.

°y

U0

Если ввести новую переменную z = —г , то можно свести систему (8) к одному дифферен- ^u0

циальному уравнению

‘‘ 2z‘fPoVzf-Po z +oz W+z( p+oU-oJ)

с граничными условиями

V i (0) = 0;      v i (») = 0;

z(∞) = 0;     z(0) = const.

Это уравнение представляет собой задачу на собственные значения. Существует два пути решения уравнения (10) с граничными условиями (11): поиск собственных значений матрицы, получающейся при разностном представлении уравнения (10); второй путь - как результат решения дифференциального уравнения методом Рунте – Кутта.

На рис. 1 и 2 представлены профили скорости z для различных значений g , μ_∞, γ.

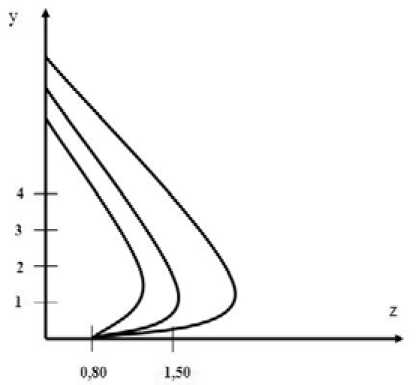
Рис. 1. График распределения скорости z при μ = 0,2, g = 2,5, γ = 1,8, α = 15, β = 0,01, ц = 0,2, g = 0,6, y = 1,8, a = 15, в = 0,01, ц = 0,2, g = 2,0, y = 1,8, ^a = 3,5, ^в = 0,01

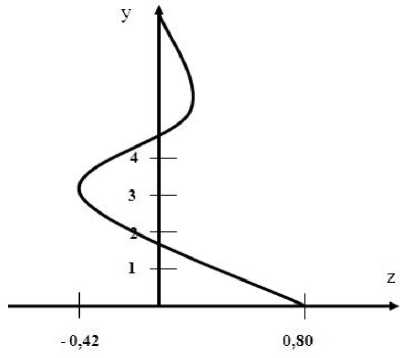
Рис. 2. График распределения скорости z при μ = 1,4, g = 1,4, γ = 1,8, α = 15, β = 0,01

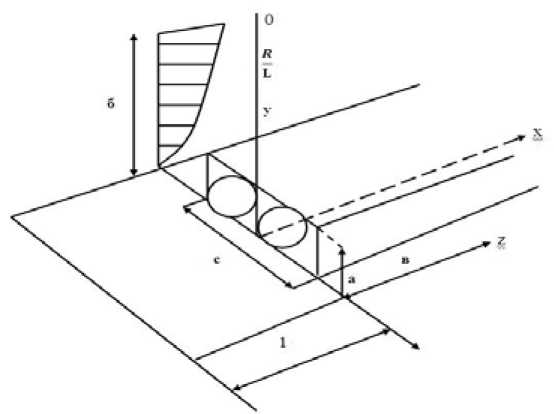
Рис. 3. Схема исследуемого течения