К вопросу повышения прочности абразивных кругов и контроля прочности композиционных абразивных материалов

Центробежные силы, действующие на абразивный круг при его вращении, вызывают в объеме круга радиальные ( σr ) и тангенциальные ( σt ) нормальные напряжения. При увеличении окружной скорости круга напряжения растут, достигая при определенном значении скорости предельного значения, приводящего к разрушению круга [1, 2]. Таким образом, допустимая окружная скорость круга косвенным образом характеризует его прочность на разрыв. Повышение прочности, а следовательно, и рабочих скоростей абразивного инструмента, является одним из важнейших направлений мировой практики абразивной обработки [3–5]. Основное преимущество высокоскоростной обработки усматривается в комбинации высокого показателя съема материала с хорошей чистотой обрабатываемых поверхностей заготовки, обеспечивающей возможность черновой и чистовой обработки заготовки с одной установки [6, 7].

Известны два направления решения рассматриваемой проблемы:

• 1)    повышение прочности композиционного материала круга;

• 2)    снижение напряжений во вращающемся круге.

В основе первого направления лежит повышение прочности материала увеличением его плотности, оптимизацией состава структуры и т. д. [8–12]. В основе второго направления – снижение напряжений во вращающемся круге за счет конструктивных решений [13].

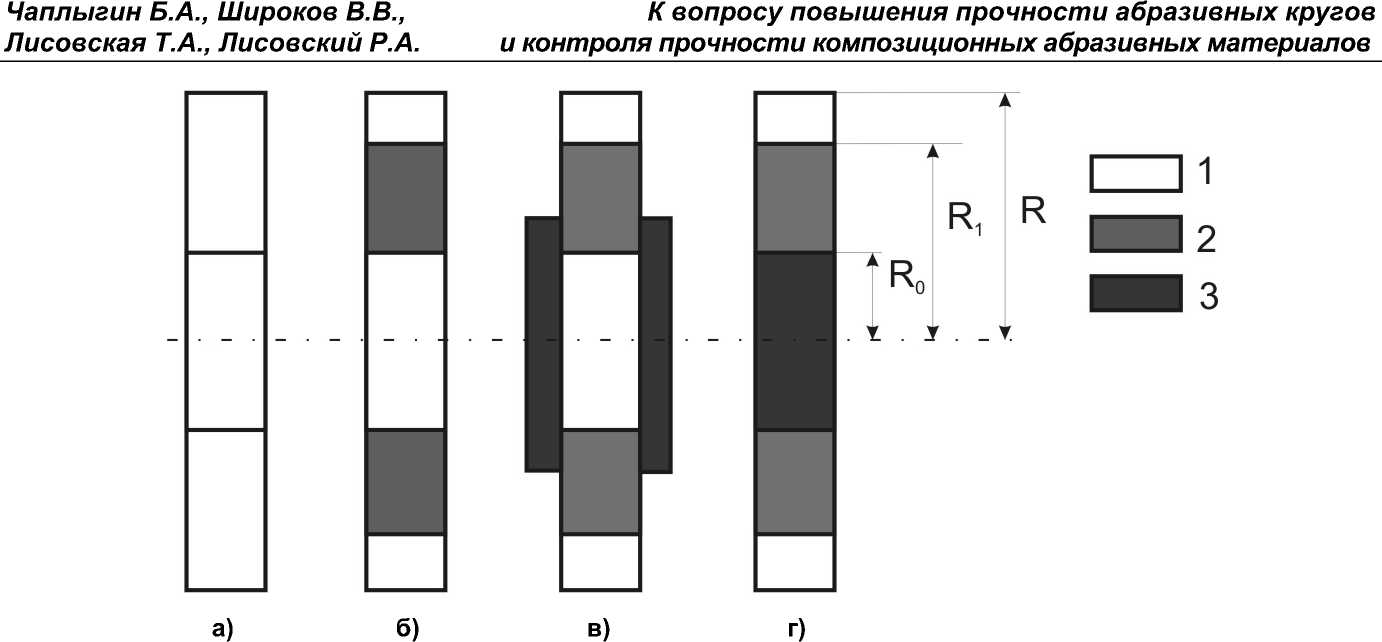
Рис. 1. К вопросу моделирования составных абразивных кругов: 1 – режущая часть, 2 – упрочняющая часть, 3 – приводная часть

К этому направлению в частности относятся составные абразивные круги [14–16]. Максимальный эффект повышения прочности абразивных кругов на основе разработок первого направления прогнозируем и достаточно ограничен, поскольку прочность абразивной смеси не может быль выше прочности наиболее прочного компонента смеси (рис. 1a).

Большими возможностями располагает второе направление, в частности работы, связанные с совершенствованием составных абразивных кругов (рис. 1б). Составной круг наряду с режущей частью имеет упрочняющуюся часть, изготовленную из более прочного материала и имеющую своей целью снижение напряжений в рабочей части круга. При этом основная задача сводится к оптимальному выбору механических и геометрических параметров упрочняющей части круга.

Определение параметров упрочняющей части составного абразивного круга

Оптимальный выбор параметров упрочняющей части в составных кругах достигается на основе анализа напряженного состояния во вращающемся круге.

Традиционно при анализе напряженного состояния принимается модель виртуально вращающегося (без приводной части) составного абразивного крута (см. рис. 1б). Подобное моделирование следует считать некорректным с точки зрения удовлетворения граничным условиям. Фактические граничные условия должны учитывать жесткую связь круга с приводным валом (в дальнейшем приводной частью круга). Например, при закреп- лении круга по схеме рис. 1, c граничное условие оr = 0 при r = R будет некорректным. Отсюда следует в частности ошибочность вывода о влиянии внутреннего отверстия круга на напряженное состояние.

Напряженное состояние составного круга, включающего приводную, упрочняющую и режущую части, описывали девятью уравнениями с шестью константами, которые определялись из граничных условий и условий неразрывности на границе составных частей круга:

E j (

• ^о r j =    2 I C 1 j ^{( 1 + ц} j ^{) -} C 2Д^{1 -ц} j ) — I-

• 1    Ц j V

pvto ²

• -    V (3+j r2;(1)

° j == r j ⁽ C j ^{( 1 +ц} j ) ⁺ C 2 j ^{( 1 - ц} j ) “2 1^-

1 H j V pvto2

• -      (3+^) r2;(2)

Urj = - ^-rj p j “2 r3 + C1 jr + C2^.(3)

8Ejr

В уравнениях (1)–(3) нижний индекс j последовательно должен принять значения p , y и v , означающие принадлежность уравнения режущей, упрочняющей и приводной части круга; C1 j , C2 j – константы, значения которых определяются граничными условиями; Urj - радиальное перемещение; Ej, ц j, p j -модули упругости, коэффициенты Пуассона и плотности материала соответствующей части значением инвариантной характеристики на- круга; r - радиальная координата; to - угловая скорость.

Для определения шести констант располагаем шестью уравнениями:

• 1)    о _{r р} = 0 при r = R ;

• 2)    ° ry = ° r р при г = R i ;

• 3)    ° ry = ° rv при ^r = R o ;

• 4)    U ry = U r р при ^r = R i ;

• 5)    U ry = U rv при r = R o ;

• 6)    U_rv = 0 при r = 0 .

Математическая модель обобщает известные модели: при Ev = Ey, pv = py описы- вает напряженное состояние виртуально вращающегося составного круга с внутренней упрочняющей частью, а при Ev = Ey = Ep, pv = py = pp - напряженное состояние обычного виртуально-вращаюшегося сплошного круга.

Имеются три характерные участка эпюр напряжений (рис. 2), принадлежащие приводной, упрочняющей и режущей частям круга. Наиболее нагруженными (опасными) сечениями являются: для режущей части - r = R _i , упрочняющей - r = R o и приводной - r = 0 .

пряженного состояния о i - интенсивностью нормальных напряжений. Для плоского осесимметричного напряженного состояния:

° i = °G r  ° r ° t + ° t .

Задача свелась к минимизации целевой функции – интенсивности нормальных напряжений в опасном сечении режущей части круга при наличии трёх управляющих факто-р° ^В R i , ^E y , P y .

Поиск минимального значения целевой функции при наличии ограничений осуществлялся с помощью программных средств Mathcad Pro.

Впервые установлено, что для каждого значения R ₁ существует множество оптимальных сочетаний модуля упругости и плотности материала упрочняющей части, обеспечивающих одно и то же минимальное значение целевой функции. Возможность минимизации целевой функции до некоторого определенного уровня на основе выбора материала упрочняющей части круга, допускающего различные комбинации модуля упругости и плотности, является весьма важным в практическом отношении, так как упрощает процедуру поиска такого мате-

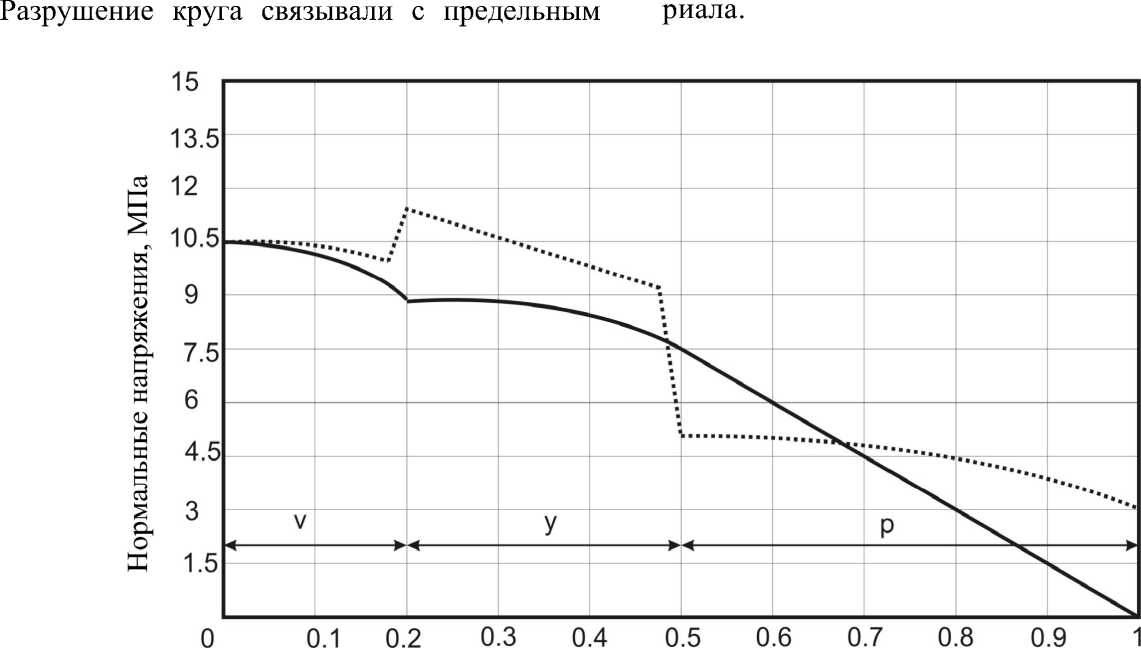
Относительная радиальная координата (r/R)

Рис. 2. Эпюры радиальных (сплошная линия) и тангенциальных (пунктирная) напряжений в круге, состоящем из приводной, упрочняющей и рабочих частей

( E y = 2,2 E p , p y = 1,35 p p )

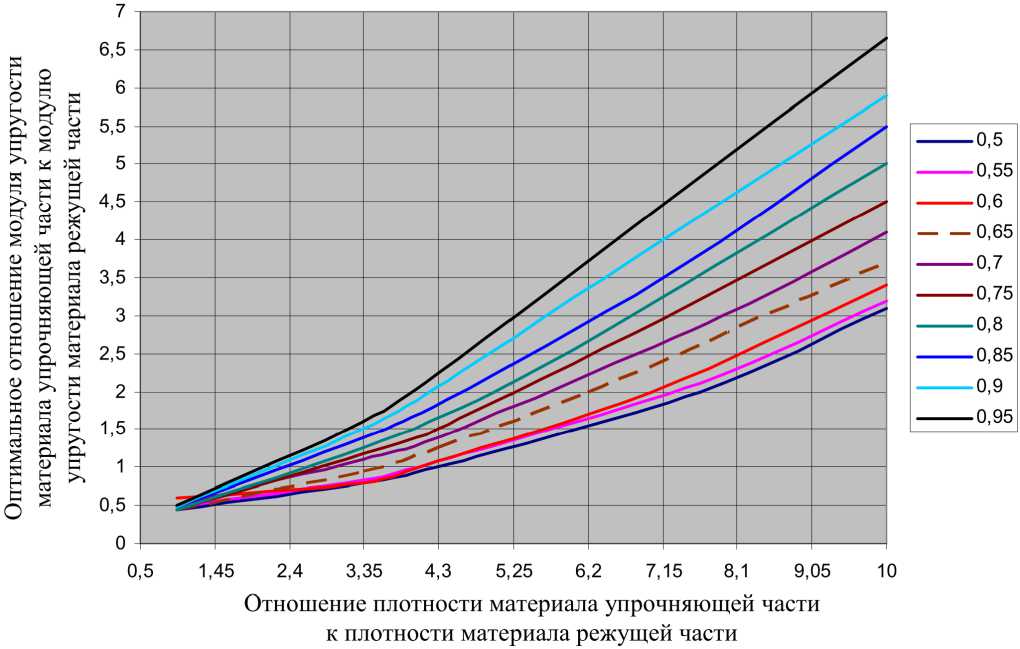
Рис. 3. Номограмма для определения оптимального сочетания плотности и модуля упругости материала упрочняющей части при различных значениях R i ( R = 200 мм , R ₀ = 80 мм , E p = 10 5 МПа , р p = 2,4 г/см 3 , о _вр = 20 МПа )

Получена номограмма для определения оптимального сочетания управляющих факторов (рис. 3), а также уравнение регрессии:

Е = Е yonm p

р y R aQ + ax -^- + a2 ~ + a 0    1 р p    2 R

p y

+

к^Р Р J

I R i

+ a + a=i

⁴ 1 R )     5

р y R р p ^R

где a ₀ , a ₁ , …, a ₅ – числовые коэффициенты.

Установлено, что увеличением радиуса упрочняющей части в сочетании с оптимизацией механических характеристик ее материала допустимая разрывная скорость круга может быть увеличена в несколько раз.

Разработана математическая модель напряженного состояния торцешлифовального абразивного круга с наружной упрочняющей частью.

В отличие от кругов с внутренней упрочняющей частью минимальное значение интенсивности нормальных напряжений в опасном сечении режущей части круга ( r = R q ) всегда достигается при наименьшей плотности и наибольшем модуле упругости. Иначе

говоря, в рассматриваемом случае отсутствует экстремум (минимум) целевой функции и взаимосвязь плотности и модуля упругости, которая бы обеспечивала минимальное значение напряжений в опасном сечении круга. Практически это означало бы, что из арсенала имеющихся материалов для упрочняющей части необходимо выбирать материал, характеризующийся максимальным модулем упругости, минимальной плотностью и обладающий необходимой прочностью. Анализ показал, что увеличение радиуса наружной упрочняющей части способствует снижению напряжений в опасном сечении круга, однако эффект снижения напряжений падает по мере увеличения радиуса, экспоненциально приближаясь к некоторому пределу. Сформулированы рекомендации по параметрам торцешлифовальных кругов с наружной упрочняющей частью.

Метод определения предела прочности абразивного материала

Основным показателем прочности абразивного круга в настоящее время является разрывная скорость круга. Указанный показа-

тель прочности является косвенным и характеризует прочность круга, а не прочность материала круга. Разрывная скорость круга определяется не только пределом прочности материала круга, но его размерами и конструкцией [17]. В связи с этим разрывная скорость круга позволяет лишь качественно судить о прочности материала круга, ограничивая возможности при принятии решений, направленных на повышение прочности материала круга.

Разрушение материала следует отождествлять с достижением в опасном сечении критического значения интенсивности нормальных напряжений (формула (4)). Критическое значение интенсивности нормальных напряжений, при котором происходит разрушение, вероятно, следует рекомендовать в качестве прямого показателя прочности материала и отождествлять с пределом прочности материала на разрыв. Суть предлагаемого экспериментально-аналитического метода определения предела прочности абразивного материала состоит в следующем.

Абразивный круг испытывают на разрыв, т. е. экспериментально определяют окружную скорость, при которой круг разрушается. Зная разрывную скорость, рассчитывают в опасном сечении режущей части круга интенсивность нормальных напряжений по формуле (4), величина которой полагается равной пределу прочности материала круга на разрыв.

Традиционные методы определения механических характеристик материалов, хорошо зарекомендовавшие себя при испытаниях металлов и сплавов, при испытании абразивных материалов не показали себя как надежные методы, обеспечивающие стабильность и необходимую точность результатов. Среди известных методов предпочтение отдают испытаниям на изгиб – методу, который также имеет серьезные недостатки.

Предлагаемый метод следует оценивать как альтернативу известным методам, выгодно отличающийся тем, что его реализация не требует специального оборудования и специальных исследований, так как предлагаемый метод сводится к дополнительной несложной аналитической обработке результатов уже существующих испытаний кругов на разрывную скорость.

Выводы

• 1.    Установлено, что для каждого значения радиуса упрочняющей части существует множество оптимальных сочетаний модуля упругости и плотности материала упрочняющей части, обеспечивающих одно и то же минимальное значение целевой функции.

• 2.    Установлено, что увеличением радиуса упрочняющей части в сочетании с оптимизацией механических характеристик ее материала допустимая разрывная скорость круга может быть увеличена в несколько раз.

• 3.    Предложен экспериментально-аналитический метод определения предела прочности абразивного материала.