К вопросу проектирования устойчивой структуры сети беззапросных измерительных средств наземного комплекса управления

DOI:

Одной из проблем при создании систем управления и организационнотехнологических комплексов является выбор их структуры, которая определяет состав элементов системы с соответствующими взаимосвязями и с учетом динамики их функционирования [1-4]. В полной мере это относится и к актуальным задачам синтеза структуры автоматизированных систем управления (АСУ) автономными объектами [57], включая АСУ космическими аппаратами (КА) [8-10] и методов построения модернизированной сети беззапросных измерительных средств наземного комплекса управления (НКУ) навигационных станций (НС) космического комплекса (КК) системы ГЛОНАСС [11].

Топология сети навигационных станций визуально представлена на рисунке 1.

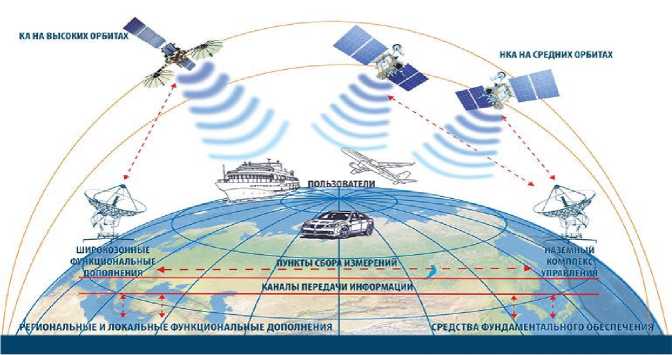
Рисунок 1. Визуализация топологии сети НС КК ГЛОНАСС. Figure 1. Visualization of the GLONASS NS network topology.

В соответствии с требованиями тактико-технического задания, наземный сегмент системы ГЛОНАСС должен обладать избыточным уровнем устойчивости, обеспечивающим его достаточное функционирование во все периоды выполнения целевых функций [11-15].

Проблемы выбора структурного состава наземного сегмента космического комплекса системы и мест дислокации его объектов актуальны для среднесрочной перспективы. В связи с этим предлагаемая формальная модель носит частный характер и, соответственно, потребует уточнения по результату проведения детального анализа при проведении модельных экспериментов с учетом результатов проводимых опытноконструкторских работ. Очевидно, что из центра управления сетью в режиме реального времени и в автоматизированном режиме решаются практически все основные навигационные задачи управления НС и контроля навигационного поля.

МАТЕРИАЛЫ И МЕТОДЫ

Работы [16-18] представляют различные пути решения задач структурного синтеза. Сгруппировать их можно следующим образом, как представлено на рисунке 2.

Рисунок 2. Типы задач структурного синтеза.

Figure 2. Types of structural synthesis problems.

Методы построения модернизированной сети беззапросных измерительных средств наземного комплекса управления навигационных станций космического комплекса требуют совместного использования оптимизационных (ОМ) и имитационных моделей (ИМ). Это связано с тем, что при формальном описании динамики функционирования системы в рамках большинства практических задач могут быть использованы только методы имитационного моделирования [19-22]. В отличие от математических моделей, представляющих собой аналитические зависимости, которые можно исследовать с помощью достаточно мощного математического аппарата, ИМ, как правило, позволяют проводить на них лишь одиночные испытания, аналогично однократному эксперименту на реальном объекте. Поэтому для более полного исследования и получения необходимых зависимостей между параметрами требуются многократные испытания ИМ, число и продолжительность которых во многом определяется возможностями используемого аппаратно-программного обеспечения, а также свойствами самой ИМ.

Типы задач структурного синтеза, представленные выше, свидетельствуют о целесообразности использования ИМ, так как это тот случай, когда возможности методов исследования системы с помощью аналитических моделей ограничены, а натурные эксперименты с учетом территориально распределенной структуры системы и ее целевого назначения либо нежелательны, либо невозможны.

Комбинация ИМ и ОМ также обоснована в тех случаях, когда создание аналитической модели для исследования конкретной системы в принципе возможно (в качестве компонента комбинированной модели), но имитационное моделирование может оказаться предпочтительным по временным затратам на проведение исследования [19].

Отметим, что для многих задач, возникающих при синтезе структур и проектировании модернизированной сети беззапросных измерительных средств наземного комплекса управления навигационных станций космического комплекса, имитационное моделирование оказывается единственным практически реализуемым методом исследования. Этим в значительной степени объясняется непрерывно возрастающий интерес к совершенствованию ИМ и расширению класса задач, для которых данный подход применяется [22].

В нашем случае при выборе и формировании структуры НКУ сети НС КК следует выделить этап формирования управляемой системы (этап 1) и этап формирования структуры управляющей системы (этап 2), характеристики которых представлены на рисунке 3.

Этап 1

•Формирование структуры управляемой системы, включая определение оптимального состава и взаимосвязей ее элементов, оптимального разбиения множества управляемых объектов на отдельные подмножества, обладающие заданными характеристиками

Этап 2

•Формирование структуры управляющей системы, включая выбор числа уровней и подсистем (иерархии управления), способов согласования целей подсистем различных уровней; оптимальное распределение выполняемых функций между уровнями и узлами системы; выбор структуры системы передачи, обработки и обмена информации

Рисунок 3. Формирование структуры системы.

Figure 3. Formation of the system structure.

В работах [10, 22-24] рекомендуется основное внимание уделять развитию методологии формирования структуры НС КК системы ГЛОНАСС на базе сочетания ОМ и ИМ. Это позволяет в полной мере учитывать динамику функционирования системы управления и ее элементов на этапе проектирования модернизированной сети беззапросных измерительных средств наземного комплекса управления навигационных станций космического комплекса системы ГЛОНАСС.

При этом отметим, что данная система относится к подклассу систем, ориентированных на как на системное (см. рис 3, этап 1), так и логическое моделирование (см. рис 3, этап 2). Только в результате рационального сочетания моделей (ОМ и ИМ) при проектировании возможно получение оптимальных (рациональных) вариантов проектируемой структуры НС КК системы ГЛОНАСС.

К подклассу системного моделирования относят системы с хорошо развитыми общеалгоритмическими средствами с возможностью использования специальных языков и систем моделирования. К подклассу логического моделирования относят системы, позволяющие в удобной форме отражать логические и топологические особенности моделируемых объектов, например, с использованием графоаналитических методологий (GERT-моделирование и моделирование сетей с GERT-подобной узловой логикой). Важность этого подхода отмечается в [7, 25, 26], так как при синтезе сложных структур учет динамики функционирования элементов системы только в простейших случаях может осуществляться аналитическими методами. Отметим, что одной из сильных сторон GERT-сетей является графическое представление, которое интуитивно понятно и легко для понимания проектировщикам и разработчикам НКУ НС КК. Модели GERT-сетей, представленные в [7, 25, 26], адаптированы для моделирования процессов управления, информационных и программных систем, что означает расширение графического представления GERT-сетей с учетом особенностей процессов данного класса. На базе данных расширений развиваются новые подходы к разработке математических моделей развития структур и процессов в сложных системах с использованием Z-преобразования и модифицированного правила Мейсона. Метод организации контрольных точек в GERT-сетях с одновременным наложением ограничений на их структуру позволяет разделять сеть на параллельные фрагменты. Каждый из них генерируется простым s-t-путем от исходного узла s до конечного узла t. Такой путь может иметь общие узлы с некоторой петлей первого порядка. Важно, что GERT-сети могут включать неделимые операции, имеющие длительное время выполнения. T устанавливается равным максимальному из множества возможных решений Ti. Это позволяет реализовать метод организации контрольных точек с минимальными структурными ограничениями для GERT сети, что упрощает процесс моделирования структуры НС КК с учетом динамики функционирования системы и ее структурных элементов на этапе проектирования модернизированной сети.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Рассмотрим аспект устойчивости функционирования данного класса сложных систем, к которому относится сеть беззапросных измерительных средств наземного комплекса управления. Известно [27], что проблема повышения эффективности целевого функционирования данного класса систем, включая структуру НС КК, тесным образом связана с обеспечением устойчивости их функционирования в условиях воздействия различного рода дестабилизирующих факторов. Ряд авторов отмечает [1, 2, 21-23, 27], что отсутствие в настоящее время конструктивных методов оценки устойчивости функционирования систем объясняется трудностями в описании их поведения и недостаточной формализацией понятия устойчивости применительно к подобного рода системам. Возможные подходы к определению основных понятий, касающихся устойчивости функционирования сложных систем, как правило, базируются на общей теории систем.

Общепринятым является определение, согласно которому устойчивость связывается со свойством системы выполнять возложенные на нее функции, несмотря на отклонение в ее структуре или организации. То есть, если система после внесения в нее «малых» структурных изменений продолжает функционировать с достаточной эффективностью, то она полагается устойчивой. В противном случае – неустойчивой. В устойчивых системах небольшие изменения в структуре оказывают пренебрежимо малое влияние на поведение системы. Если система устойчива, то нет необходимости использовать корректирующие воздействия для преодоления отклонений в системе.

Определение устойчивости зависит как от типа системы, так и от принципов оценивания отклонений в поведении системы и изменений результирующих показателей под действием возмущений.

Подобную оценку предлагается формулировать на соответствующим образом определенном понятии окрестности. При этом полагается, что система устойчива относительно введенного понятия окрестности, если при достаточно малых изменениях в структуре системы достаточно малы изменения в ее функционировании. Это полностью согласуется с классическим определением устойчивости по Ляпунову [27].

Формализация данного подхода в рамках общего понятия устойчивости систем выглядит следующим образом. Пусть q соответствующим образом описывает состояние системы, а z – некоторый результат ее функционирования. Предположим, что существует отображение П, такое что z = П(q).

Система считается устойчивой, если незначительные отклонения от z вызываются малыми отклонениями от q . Для того, чтобы была возможность судить о близости или малости отклонений в рамках формализации необходимо определить понятие окрестности точек q и z . Можно использовать формализацию, предложенную в [27] для определения системы окрестностей. В рамках же данного исследования нас интересует в большей мере анализ понятия устойчивости, связанное главным образом со строением системы, то есть ее структурой. Часто это понятие именуется структурной устойчивостью системы. В общем виде имеет место отношение

S ^ D x E, где D – входные и E – выходные структурно связанные объекты системы.

Обозначим множество всех возможных состояний системы, заданной на множестве D и E , через S o = { S c D x E}.

Предположим, что состояние системы зависит от некоторого множества атрибутов (факторов) ATR , такого, что они определяют текущее состояние системы, то есть существует отображение

P : ATR ^ S o .

Далее будем полагать, что результативность функционирования системы, заданная множеством M , определяется состоянием системы, иначе говоря, имеется отображение

F : S o -9- M.

Следующим важным моментом является формирование системы окрестностей для точек множества ATR и M относительно заданных семейств подмножеств R atr и R m. Выбор заданных семейств подмножеств - это один из наиболее трудоемких этапов. Однако их выбор по сути дела сразу устанавливает границы устойчивости системы. Сложность выбора указанных семейств подмножеств R atr и R m в значительной мере усугубляется отсутствием меры близости в оценке результативности функционирования системы по целевому назначению. В рамках многоатрибутивного подхода (например, с использованием модифицированного TOPSIS-метода [28, 29]) такая мера определяется исходя из конечного набора рациональных вариантов структуры. Тогда можно предположить, что выбор семейств подмножеств R atr и R m сделан. Следовательно, можно утверждать, что система устойчиво функционирует с показателем или результатом m о е M в условиях atr о е ATR , если для любого элемента m е On( m о ) существует элемент ATR i е Оп( atr о ), такой, что для всех atr е ATR 1 будет выполняться F ° P ( atr ) е m .

В [27] предлагается ввести отношение порядка, которое сопоставляется отношению <  atr , которое частично упорядочивает множество ATR по правилу atr i <  atr atr 2 . Это является важным моментом при выборе заданных семейств подмножеств R ATR и R M . То есть, отношение порядка ≤ ATR , заданное на множестве атрибутов ATR , позволяет формировать семейства подмножеств с учетом изменения структуры системы, что в свою очередь позволяет факторизовать множество атрибутов ATR по структурным характеристикам.

Относительно множества M отметим, что построение семейства подмножеств Rm должно опираться на исследования по оценке устойчивого целевого функционирования сети беззапросных измерительных средств наземного комплекса управления космической системы. В рамках такого исследования важно опираться на существующий в настоящее время широкий спектр подходов к решению проблемы, связанной с заданием отношений предпочтения на множестве, оценивающем результативность системы [17-20, 27]. Получение более конструктивных определений в рамках введенных структур представляется возможным только путем уточнения по результатам проведения детального анализа при проведении модельных экспериментов с учетом проводимых опытно-конструкторских работ при создании проекта структуры сети беззапросных измерительных средств наземного комплекса управления. В качестве базового определения, обладающего достаточным конструктивизмом, целесообразно принять определение, приводимое в [27], так как на его базе можно эффективно разработать практические методы оценки устойчивости функционирования системы.

Для решения задач выбора структуры НС КК системы ГЛОНАСС предлагается многоатрибутивный оптимизационно-имитационный подход (МАОИП), основанный на совместном использовании оптимизационных и имитационных моделей в процессе поиска оптимальных вариантов структуры [10, 21-23].

Шаги 1-3 для МАОИП при выборе базового множества структур НС КК системы ГЛОНАСС с заданным набором атрибутов для многоатрибутивного выбора лучшего варианта структуры представлены на рисунке 3.

Шаг 1

Шаг 2

Проверка допустимости варианта структуры по аналитически заданным атрибутам

Шаг 3

Рисунок 4. Шаги 1-3 выбора базового множества структур НС КК.

Figure 4. Steps 1-3 of selecting the basic set of structures of the navigation system of the space complex.

Проведение компьютерного эксперимента с имитационной моделью системы для допустимого по аналитически заданным атрибутам варианта структуры

На первом шаге осуществляется синтез варианта структуры системы S i , i = 1, …, s с заданным набором атрибутов ATR j , j = 1, …, J . На втором шаге выполняется проверка допустимости варианта структуры по аналитически заданным атрибутам. Если S i Е М, то переход к шагу 3, в противном случае возвращаемся к шагу 1. Третий шаг предполагает проведение компьютерного эксперимента с имитационной моделью системы N для допустимого по аналитически заданным атрибутам варианта структуры S i . Модель N отображает функционирование моделируемой системы для различных вариантов структуры. Между шагами 1 и 3 организуется информационный интерфейс для передачи данных об исследуемом варианте структуры S i .

Заключительным шагом является проверка допустимости варианта структуры S i алгоритмически заданным атрибутам. Если S i Е М. Вариант структуры, допустимый с учетом как аналитически, так и алгоритмически заданных атрибутов, запоминается. Полученные результаты с учетом того, что все варианты структуры проанализированы, выдается по окончании работы алгоритма.

В работе рассматривается применение ОИ и ОМ в рамках подхода МАИОП к решению задач формирования структур НС КК системы ГЛОНАСС как к распределенным информационно-управляющим системам. НС КК системы ГЛОНАСС представляет собой рассредоточенные в пространстве многофункциональные совокупности стационарных и подвижных элементов с развитыми техническими средствами приема, передачи и обработки информации.

В работах [28, 29] для решения поставленных задач используется модифицированный TOPSIS метод многоатрибутивного принятия решений. Для определения характеристик и выделения вариантов построения отдельных контуров управления системы используется известная модель оптимизации структуры контура управления [23].

Многоатрибутивная задача принятия решений (MADM) — это разновидность многокритериального принятия решений, когда переменные задачи дискретны, а количество сценариев/схем принятия решений ограничено. Нахождение оптимального решения или ранжирование (сортировка) решений в наборе конфликтующих и несоизмеримых конечных (бесконечных) решений является основной проблемой, успешно решаемой в рамках теории многоатрибутивного принятия решений.

На сегодняшний день существует два основных направления в теории многокритериального принятия решений: многоатрибутивные задачи принятия решений и многоцелевые задачи принятия решений. Вообще говоря, многоатрибутивная процедура принятия решений — это последовательность действий, позволяющая принять решение, выбирая оптимальную альтернативу или ранжируя набор альтернатив при условии рассмотрения нескольких атрибутов. Как правило, переменные задачи дискретны, а количество альтернатив ограничено.

Отметим также существующий подход в виде многоцелевой задачи принятия решений (MODM), который требует одновременного рассмотрения двух или более целей, когда переменные задачи непрерывные и имеется бесконечное количество альтернатив. TOPSIS — это многоатрибутивный метод принятия решений, который ранжирует альтернативы по атрибутам путем расчета метрического расстояния от идеальной альтернативы. Часто данный метод применяется в комбинации с TODIM, когда решения ранжируются и выбираются, исходя из степени глобального доминирования.

Таким образом, TOPSIS — это метод принятия решений для ранжирования или сортировки путем приближения к идеальному решению. Он использует положительные и отрицательные идеальные решения многоатрибутивной задачи для ранжирования альтернатив в заданном наборе.

Идеальное решение X + — это значение многоатрибутивной оценки, соответствующее виртуальному оптимальному решению A +, которое не обязательно существует в наборе A , и каждое значение атрибута в A + является оптимальным значением атрибута в матрице решений.

Отрицательное идеальное решение X - — это значение многоатрибутивной оценки, соответствующее виртуальному наихудшему решению A -, которая не обязательно существует в наборе схем A , и каждое значение атрибута в A - является наихудшим значением атрибута в матрице решений. То есть, метод TOPSIS сравнивает каждую альтернативу из набора A с положительными и отрицательными идеальными решениями, и альтернатива, которая одновременно близка к идеальному решению и далека от отрицательного идеального решения, является лучшим структурным решением из набора допустимых структур НС КК.

Метод TOPSIS иногда относят к классу методов компенсаторной агрегации, так как он допускает компромиссы между атрибутами, когда плохой результат по одному атрибуту может быть сведен на нет хорошим результатом по другому атрибуту. Это обеспечивает более реалистичный подход к моделированию, чем некомпенсаторные методы.

Топологическая структура НС КК системы ГЛОНАСС определяет взаимное расположение и количество пунктов сети (ПС) комплекса управления системы для заданных типов КА.

Задача формирования топологической структуры НС КК системы ГЛОНАСС заключается в следующем: для заданных множеств КА различных типов Е_КА, множества участков возможной доступности L , графика движения G_k и программы работ n_fc КА каждого типа необходимо найти минимальную по затратам на создание совокупность ПС, чтобы при этом выполнялись требования к управляемости и коэффициенту доступности для заданных типов КА (устойчивость системы), загрузке ПС с учетом специальных требований к системе (например, доступность на одном витке КА не менее чем двумя ПС (структурная избыточность), минимально допустимое время нахождения КА в зоне какого-либо ПС и т. д..

В результате решения данной задачи определяется, какие ПС необходимы в системе и с какими типами КА они будут взаимодействовать.

В рамках TOPSIS методологии определяются положительные и отрицательные идеальные решения для топологической структуры НС КК. На основе модельных данных нормализуется матрица решений и строится матрица взвешенной нормы. Используя результаты расчета матрицы взвешенной нормы, вычисляются положительные и отрицательные идеальные решения для топологической структуры НС КК в заданной ситуации, определяющей затраты на создание ПС, требования к управляемости и доступности (устойчивости) системы и т.д.

Как уже отмечалось, наземный сегмент системы должен обладать избыточным уровнем устойчивости, обеспечивающим его достаточное функционирование во все периоды выполнения целевых функций. В рассматриваемой постановке мы опираемся на обобщенную модель иерархической системы резервирования, которая представлена на теоретико-множественном уровне в [27]. В частности, структура системы может описываться древовидным графом с корнем, соответствующим подсистеме верхнего уровня.

Анализ возможных дестабилизирующих факторов, воздействующих на систему, исходит из следующих положений. В первом приближении можно считать, что возможные изменения в такой системе резервирования связаны с нарушением связей между подсистемами (эффект «стирания» ребер в графе структуры) и частичным или полным переходом «запасов» (резервных элементов) в недоступное для использования состояние. При этом, с точки зрения целевого функционирования системы, анализ нарушений связей между подсистемами показывает, что воздействия этого типа соответствуют переходу на некоторое время, до восстановления структуры резервов в подсистемах верхних уровней (над узлом разрыва) в состояние, недоступное для использования в соответствующей части обеспечиваемых объектов. Тогда можно полагать, что воздействие на систему заключается в изменении состояния резервов в подсистемах на некотором интервале времени.

С помощью разработанных систем поддержки принятия решений [30, 31] при выборе структуры НС КК системы ГЛОНАСС был проведен ряд компьютерных экспериментов по формированию и оптимизации топологической структуры распределенной сети навигационных станций.

Рассматривается пример формирования НС КК системы ГЛОНАСС, которая включает совокупность наземных пунктов, осуществляющих навигацию и управление КА трех типов, имеющих соответствующие орбиты с заданными периодами обращения.

Задана следующая исходная информация: множество возможных ПС; затраты на создание j -го ПС (табл. 1); множество участков возможной доступности (УВД) и времена доступности КА (табл. 2); количество КА каждого типа и множество возможных пунктов для каждого типа КА.

Таблица 1. Условные единицы затрат на проектирование ПС.

• Table 1.    Conventional units of costs for designing system points.

Пункты системы  ПС-1  ПС-2  ПС-3  ПС-4  ПС-5  ПС-6  ПС-7

Затраты          300   500    400    450    500    550350

Таблица 2. Доступность КА на участках возможной доступности.

• Table 2.    Availability of spacecraft in areas of possible accessibility.

Участки возможной доступности

Тип КА 001  002 003  004 005  006 007 008009

КА-1      11    6     7     -     -     -     -     --

КА-2      -     -     -     6     7     7     -     --

КА-3      -     -     -     -     -     -     6     77

В таблице 3 представлены модельные временные и территориальные ограничения КА:

• •    ограничения на глобальность Н_к(к = 1,3);

• •    ограничения на количество ПС (минимальное количество ПС, необходимых для навигации и управления КА), М_к(к = 1,3) для k -го типа КА;

• •    ограничения    на    продолжительность    навигационно-управляющего

взаимодействия для КА k -го типа т_к т _п(к = 1,3).

Таблица 3. Модельные временные и территориальные ограничения КА.

Table 3. Model time and territorial restrictions of the spacecraft.

Тип КА	H k	M k	^ kmin	Время взаимодействия τ k
КА-1	0,6	1	9	15
КА-2	0,7	2	10	12
КА-3	0,6	3	9	14

В результате компьютерных экспериментов выполнен расчет и получено следующее решение, которое представлено в таблице 4 и которое характеризует пункты сети по участкам доступности с учетом трех типов КА.

Таблица 4. Экспериментальные результаты для модельного прототипа.

Table 4. Experimental results for the model prototype.

Тип КА	Участки доступности L k	ПС m k
КА-1	1, 3	1, 3
КА-2	5, 6	3, 4
КА-3	7, 8, 9	3, 6, 7

Результаты анализа указывают на то, что для данного модельного прототипа НС КК, некоторые пункты сети навигационных станций, являясь структурно избыточными, не являются обязательными для устойчивого функционирования НС КК во все периоды выполнения целевых задач. В частности, пункты 2 и 5 могут быть переведены в резерв или полностью исключены из системы. Это не окажет какого-либо негативного влияния на устойчивость системы при выполнении установленных функций.

ЗАКЛЮЧЕНИЕ

На основании приведенного в статье анализа существующих подходов к структурному проектированию модернизированной сети беззапросных измерительных средств наземного комплекса управления НС КК подтверждена обоснованность совместного использования оптимизационных и имитационных моделей. Их комбинация реализована в рамках многоатрибутивного оптимизационноимитационного подхода. Это позволяет находить рациональный вариант структуры проектируемой системы, то есть в процессе формирования конструировать, оценивать и отбирать рациональные варианты структуры НС КК системы ГЛОНАСС. Шаги МАОИП повторяются итерационно, что позволяет в полной мере учитывать свойства моделируемых объектов, а имитационная составляющая содержит случайные переменные, описывающие как функционирование самих систем, так и воздействия внешней среды. Это важно на этапе формирования базового множества структур НС КК системы ГЛОНАСС, позволяя с использованием ИМ отсеивать варианты структур, исходя, в том числе, из аналитически заданных ограничений на атрибуты модели.

Использование систем программной поддержки многоатрибутивного принятия решений позволило показать на модельном прототипе системы экспериментальный выбор лучшего варианта построения сети НС КК.

Отметим, что в связи с тем, что предлагаемая формальная модель носит частный характер и требует уточнения по результату проведения детального анализа при выполнении опытно-конструкторских работ, данный подход, основанный на макетировании (прототипировании) проектируемой системы и соответствующих компонентов управляемых объектов, имеет наглядную и понятную заказчику форму демонстрации работы проектируемой системы. Это окажет существенную помощь при согласовании проектных решений, так как появляется возможность выявить и устранить потенциальные неувязки и ошибки на более ранних стадиях проектирования. Это, как известно, существенно снижает затраты на их исправление.