К вопросу прогнозирования технического состояния жидкостных ракетных двигателей малой тяги

Введение. Данная статья продолжает работы [1; 2], в которых была рассмотрена задача балансировки в динамическом режиме с обеспечением минимального смещения центра масс с геометрической оси, стабилизированной вращением конической летающей модели (ЛМ), конус корпуса которой характеризуется малым полууглом раствора. Балансировка выполняется на заключительном этапе общей сборки модели. В соответствии с алгоритмом, приведённым в [1], модель балансируется в составе сборного ротора, на низкочастотном динамическом балансировочном стенде с газовыми опорами и вертикальной осью вращения [3; 4]. Процесс балансировки предполагает определение и последующее приведение параметров массо-инерционной асимметрии модели, к числу которых относится величина поперечного смещения центра масс с геометрической оси и угол отклонения продольной главной центральной оси инерции (ГЦОИ) относительно той же оси [5; 6] к значениям, не превышающим заданных в эксплуатационной документации на модель предельно-допустимых значений. Наличие единственной плоскости коррекции не позволяет полностью совместить продольную ГЦОИ с геометрической осью ЛМ, обычно выбираемой в качестве строительной оси. Вариант балансировки с оптимизацией по критерию достижения минимально возможного для конкретной конструкции ЛМ смещения центра масс обычно выбирают, учитывая существенное влияние данного параметра на лётно-технические характеристики модели [7].

Приведение параметров к заданным нормативам выполняется путём корректировки массы модели, для чего к штатной плоскости коррекции модели, которая у конических ЛМ, как правило, располагается на торце (или вблизи торца), на значительном расстоянии от её центра масс прикрепляют балансировочный груз. При этом масса и угловое положение балансировочного груза рассчитывается по результатам измерений векторов дисбалансов , действующих в двух - в верхней (штатной) и нижней (далее обозначаемых соответственно индексами В и Н) - плоскостях коррекции сборного ротора, в состав которого входит контролируемая модель [8; 9]. В качестве нижней плоскости коррекции используется нижний торец специализированного технологического переходника, внутри которого (вертикально, носком вниз) устанавливается ЛМ. Измерения амплитуд и фаз вибраций верхней и нижней опор, пропорциональных значениям и углам векторов дисбалансов, действующих В , проводят на выбеге сборного ротора, на постоянной рабочей частоте вращения [10; 11]. Методика предполагает сначала - приведение контролируемой ЛМ расчётным путём в состояние квазистатической неуравновешенности, а затем - моделировании состояния моментной неуравновешенности (исключающей поперечное смещение центра масс) с расчётом предполагаемого угла перекоса продольной ГЦОИ относительно геометрической оси модели. В случае если этот угол не превышает предельно-допустимого значения, то рассчитывают параметры балансировочного груза и проводят корректировку массы ЛМ. А если превышает, то рассчитывают предполагаемую (одновременно являющуюся минимально возможной для данного варианта компоновки модели) величину поперечного смещения центра масс, задавая значение угла перекоса продольной ГЦОИ равным предельно-допустимому значению. Если при этом предполагаемый угол перекоса продольной ГЦОИ не превышает заданного предельнодопустимого значения, то рассчитывают параметры балансировочного груза и проводят корректировку массы ЛМ. В ином случае балансировку прекращают, а ЛМ отправляют изготовителю на перекомпоновку. Методика защищена патентом РФ № 2499985 [12].

Однако существуют летающие модели, в том числе обладающие конической формой корпуса, для обеспечения динамической устойчивости и, соответственно, эффективности эксплуатации которых более предпочтительным является минимизация именно перекоса продольной ГЦОИ относительно геометрической оси (при одновременном выполнении заданного норматива по величине поперечного смещения центра масс). В данной статье предлагается рассмотреть модификацию алгоритма балансировки ЛМ [7; 12], которая ориентирована на решение задачи балансировки с приведения параметров массо-инерционной асимметрии к значениям, не превышающим заданных предельно-допустимых значений этих параметров, но с оптимизацией по критерию достижения минимально возможного для контролируемой конструкции перекоса продольной ГЦОИ относительно геометрической оси модели. Рассматривается вариант задачи, когда имеется априорная информация о массе, продольном положении центра масс относительно обеих плоскостей коррекции и моментах инерции контролируемой модели, полученной с использованием другого оборудования и средств измерений [8; 13; 14], а также о балансировочных коэффициентах измерительной системы, полученной при настройке стенда на объект контроля с использованием пробных грузов [15; 16].

Алгоритм балансировки. Предлагаемый алгоритм предполагает выполнение двух пусков сборного ротора в исходном состоянии – с поворотом ЛМ на 180о вокруг геометрической оси внутри технологического переходника. По результатам измерений вибраций опор вычисляют параметры начальных дисбалансов DНАЧ и DНАЧ , действующих в плоскостях коррекции, а также рассчитывают начальные параметры радиуса-вектора р поперечного смещения центра масс и вектора-угла перекоса продольной ГЦОИ модели агл относительно её геометрической оси по формулам [15]

Р

НАЧ    НАЧ

₍НАЧ _ D B  + D H

M

;

НАЧ аГЛ

НАЧ      НАЧ

• 1    . ² ( D B   x B D H x H )

= — arcsin —------------------

• 2               A Z

где M - масса модели; AZ = I3 - Ia - разность между экваториальным Z3 и аксиальным 1а моментами инерции модели; x и x – расстояния от центра масс модели до верхней и нижней плоскости коррекции соответственно. Затем в случае, если начальное значение хотя бы одного из параметров, характеризующих асимметричность в начальном распределении масс ЛМ, превышает соответствующее предельно-допустимое значение рдоп или аглдon, заданное в эксплуатационной документации на модель, проводят балансировочный расчёт. В процессе расчёта имитируется действие дисбалансов в плоскостях коррекции, моделирующих промежуточные состояния неуравновешенности ЛМ. Результатом расчёта является либо определение массы и угла установки балансировочного груза, прикрепление которого к штатной плоскости коррекции позволяет скорректировать массу ЛМ, обеспечивая приведение значений контролируемых параметров заданным нормативам с оптимизацией по критерию достижения минимального возможного угла перекоса продольной ГЦОИ относительно геометрической оси модели, либо доказательство невозможности обеспечения одновременно двух контролируемых параметров массо-инерционной асимметрии для данной компоновки модели по заданным нормативам [7].

На первом шаге алгоритма балансировочного расчёта предполагается перевод ЛМ в режим квазистатической неуравновешенности, т. е. когда её геометрическая ось и продольная ГЦОИ пересекаются, но не в центре масс. Это позволяет при проведении дальнейших расчётов оперировать исключительно коллинеарными векторами дисбалансов, действующими в противоположных плоскостях коррекции. Для перевода ЛМ в режим квазистатической неуравновешенности следует устранить действие начального дисбаланса в верхней (штатной) плоскости коррекции, задав в ней, как было показано в [2], компенсирующий дисбаланс DКОМП , равный по значению, но противоположный по направлению начальному дисбалансу DНАЧ . При этом в нижней плоскости коррекции в соответствии с рисунком будет сформирован дополнительный дисбаланс DДПЛ1 , направленный противоположно дисбалансу DКОМП , значение которого определяется выражением

ДПЛ 1      КОМП

DH   — DB   * КНВ , где К – коэффициент влияния верхней плоскости коррекции на нижнюю плоскость коррекции при наличии дисбаланса в верхней плоскости коррекции, определяемый экспериментально в процессе предварительной настройки стенда [15–17]. Появление дисбаланса DДПЛ1, в свою очередь, обусловит формирование дисбаланса DКОМП , равного геометрической сумме дисбалансов DДПЛ1 и DНАЧ , взамен дисбаланса DНАЧ в нижней плоскости коррекции в соответствии с выражениями

КОМП       НАЧ ² ДПЛ 1² НАЧ ДПЛ 1        НАЧ    ДПЛ 1

D H   ^— ^ ^ин  + D H   + ²D H D H   cos ( P h  - P h  ) ;

КОМП

P h

sin p¹^ + sin в ДПЛ 1

— arctg    иНАЧ      оППЛ 1 , cos pH  + cos pH

где в Н^АЧ и в ДПЛ 1 — фазовые углы дисбалансов D НА ^Ч и D Д ^{ПЛ 1} соответственно. При этом, поскольку в верхней плоскости коррекции дисбаланс будет отсутствовать, то продольная ГЦОИ будет пересекаться с геометрической осью, а поперечное смещение центра масс ЛМ будет характеризоваться значением

КОМП

Р

КОМП

DН

M

На втором шаге следует смоделировать перевод ЛМ в режим статической неуравновешенности, т. е. когда продольная ГЦОИ параллельна геометрической оси и перекос между этими осями отсутствует. Для этого в штатной плоскости коррекции необходимо задать корректирующий дисбаланс D^КОРР , в соответствии с рисунком, сонаправленный дисбалансу D^КОМП и определяемый формулой

КОРР

DВ

КОМП D_Н

1 + К НВ

НВ

При этом в нижней плоскости коррекции будет сформирован дополнительный дисбаланс D^{ДПЛ 2} , направленный противоположно дисбалансу D^КОРР и определяемый выражением

ДПЛ 2      КОРР

D H     D B   К НВ .

Это, в свою очередь, обусловит формирование в нижней плоскости коррекции дисбаланса D^КОРР (взамен дисбаланса D^КОМП ), равного сумме противоположно направленных дисбалансов D^КОМП и D^{ДПЛ 2}. Значение дисбаланса D ^КОРР будет определяться выражением

КОРР    КОМП    ДПЛ 2

HНН

.

Равенство значений эквиполентных дисбалансов D^КОРР и D^КОРР обеспечивает исключение перекоса продольной ГЦОИ относительно геометрической оси и перевод ЛМ в режим статической неуравновешенности. При этом рассчитать предполагаемую величину остаточного поперечного смещения центра масс с геометрической оси ЛМ, которая появится в результате устранения поперечного смещения центра масс, можно по формуле

КОРР

_{2 D} КОРР

М

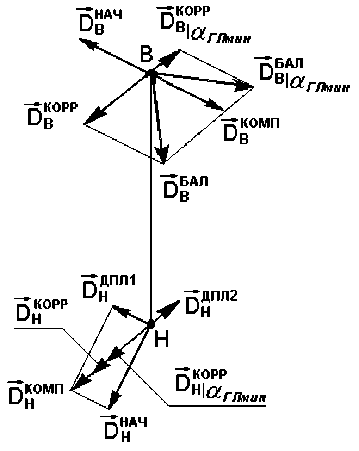
Диаграмма балансировочного расчёта

Diagram of counterbalancing calculation

В случае выполнения условия ρ ^КОРР ≤ ρ , определяют значение D ^БАЛ и угловое положение

БАЛ                                                     ^БАЛ

αБАЛ вектора балансировочного дисбаланса DВ  , используя соответствующие параметры смоделированных в штатной плоскости коррекции В векторов дисбалансов DКОРР и DКОРР

БАЛ

.

Рассчитать параметры балансировочного вектора D В , в соответствии с рисунком, представляющего собой геометрическую сумму дисбалансов D^КОМП и D^КОРР , можно по формулам

БАЛ D_В

КОМП ² D_В

КОРР ²      КОМП КОРР      КОМП    КОРР

+ d_b   + 2 d_b  d_b  cos ( а - a ) ;

а БАЛ = arctg

sin « КОМП + sin а КОР' ВВ

КОМП        КОРР , cos а + cos а

где аК°МП и аКОР’ - фазовые углы дисбалансов DК°МП и DКОРР соответственно. Тогда для случая аГПост = 0, pocn, = рКОРр < рдоп рассчитать массу балансировочного груза по формуле

БАЛ тБАЛ

DВ rB

при этом угол установки балансировочного груза на верхней (штатной) плоскости коррекции

БАЛ                 ^БАЛ

Ф_БАЛ будет совпадать с фазовым углом а_в  дисбаланса Dв  .

Далее проводят корректировку массы ЛМ, прикрепив балансировочный груз к балансировочной плоскости В, обеспечивая тем самым приведение обоих параметров массоинерционной асимметрии к значениям, не превышающим предельно-допустимых значений. При этом устраняется перекос продольной ГЦОИ относительно геометрической оси. Однако в случае, если значение рКОРР будет превышать предельно-допустимое значение рдо)t, то следует рассчитать предполагаемое минимально возможное значение угла отклонения продольной ГЦОИ относительно геометрической оси а^ин, которое может быть достигнуто путем изменения дисбаланса в плоскости коррекции В при уменьшении величины поперечного смещения центра масс ЛМ до предельно-допустимого значения рп, по формуле

КОМП

(Едоп._____Н__2 rY +к y \_п™х агЛмин =  arc sin2

, г-       ( х в ⁺ К НВ х Н ²  D H    х Н

М

В случае если полученное значение аГЛмин будет превышать заданное предельно-допустимое значение аглдон, балансировочный эксперимент прекращают, а ЛМ бракуют и направляют изготовителю на перекомпоновку ввиду доказанного расчётом отсутствия возможности одновременного приведения величины смещения центра масс и угла отклонения продольной ГЦОИ относительно геометрической оси к значениям, не превышающим заданных предельнодопустимых значений. В ином случае, то есть если неравенство |аГЛи<0Олдоп окажется верным, то определяют значение вектора дисбаланса DКОРР , обеспечивающего достижение минимального значения \агл»шн\ при установке смещения центра масс, равного роп, по формуле

КОРР

^В\^а ГЛмин

КОМП

Р доп^М - D H

1 - Кнв

НВ

при этом положительный результат расчёта будет означать, что направления этих дисбалансов

КОРР

В^{1 а} ГЛмин

и D^КОРР совпадают, а отрицательный – наоборот, что их направления противоположны.

Ввиду взаимовлияния плоскостей коррекции, в плоскости коррекции Н появится дисбаланс, D^КОРР , сонаправленный дисбалансу D^КОМП , значение которого определяют по формуле

КОРР      КОМП    ДПЛ 3

DH Оглмн« = DH   + DH   ’ где DДПЛ3 – есть значение дополнительного дисбаланса DДПЛ3 (на рисунке не показан), появляющегося в плоскости коррекции Н как следствие от действия дисбаланса DКОРР в плоскости коррекции В и противоположно направленного дисбалансу DКОРР . DДПЛ3 определяется по формуле

ДПЛ 3 D_Н

КОРР

DB О т-нн К™ '

Затем определяют значение D БАЛ и угловое положение а БАЛ вектора балансировочного дисбаланса D^БАЛ , используя соответствующие параметры смоделированных в балансировочной плоскости коррекции В векторов дисбалансов D^КОРР и D^КОМП . После чего определяют массу балансировочного груза m , установку которого производят в угловом положении, соответствующем угловому положению дисбаланса D^БАЛ . Для определения значения балансировочного дисбаланса, массы и угла установки балансировочного груза используют формулы

БАЛ

В\ ^а ГЛмин

КОМП ² КОРР ² КОМП КОРР         КОМП

D B    ⁺ D B а гл_ ^{+ 2} D B    D B а™„„ • cos ( О

—

КОРР ^a B 0^ ) ,

КОРР где а^аг^ - угловое положение дисбаланса Dв^гл ;

аБАЛ  = arctg

^B \ ^a ГЛмин

sin а КОМ' + sin ОКОР

________B__________________ ^B\ ^а ГЛмин  .

КОМП        КОРР ;

Cos ^a B    + cos ^a B а ₁^лм₁н_н

БАЛ

БАЛ     _ D^B ^г^лмлинн

B\аГЛмнн         r rB

После чего проводят корректировку массы ЛМ, прикрепив балансировочный груз к балансировочной плоскости В, обеспечивая совпадение углов установки балансировочного груза и вектора балансировочного дисбаланса, и выполняют контрольный пуск сборного ротора для подтверждения правильности проведённого расчёта. По результатам контрольного пуска определяют параметры остаточных дисбалансов DОСТ и DОСТ , действующих в соответствующих плоскостях коррекции после установки балансировочного груза, и рассчитывают (пренебрегая массой балансировочного груза как заведомо практически несущественной по сравнению с массой контролируемой ЛМ) остаточные параметры массоинерционной асимметрии по формулам:

ОСТ     ОСТ

-* ОСТ _ D B  + D H

M

ОСТ аГЛ

ОСТ       ОСТ

• 1    . ² ( D B   x B D H x H )

= — arcsin —-----------------

• 2              A Z

Работоспособность рассмотренного алгоритма можно оценить на конкретном числовом примере.

Пример расчета балансировочного груза. Проведём расчёт балансировки ЛМ при следующих значениях параметров задачи:

– масса модели М = 100000 г;

– расстояние от центра масс ЛМ до верхней плоскости коррекции x = 570 мм;

– радиус верхней плоскости коррекции r = 200 мм;

– расстояние от центра масс до нижней плоскости коррекции x = 800 мм;

– разность между экваториальным и аксиальным моментами инерции Δ I = 8,5·10⁹ г·мм²;

- предельно-допустимое значение поперечного смещения центра масс р_оп = 0,1 мм;

- предельно-допустимое значение угла перекоса ГЦОИ а_глдоп = 10' ~ 0,166667°;

– коэффициент влияния верхней плоскости коррекции на нижнюю плоскость коррекции при наличии дисбаланса в верхней плоскости коррекции К НВ = 0,3;

– начальный дисбаланс в верхней плоскости коррекции D^НАЧ = 25000 г·мм, фазовый угол a f ⁴ = 80°;

В

– начальный дисбаланс в нижней плоскости коррекции D^НАЧ = 10000 г·мм, фазовый угол

1Г и (2):

–

–

= 115°, откуда начальные значения параметров асимметрии масс ЛМ в соответствии с (1)

р^НАЧ = 0,34 мм; 0^ = 3,62 ' .'

Поскольку обнаружено, что начальные значения параметров массо-инерционной асимметрии превышают заданные предельно-допустимые значения, проведём балансировочный расчёт для достижения условий

ОСТ ^а ГЛ р ^оС

^а гЛмин ^ Р доп .

— ^аГЛдоп ;

Переведём ЛМ в состояние квазистатической неуравновешенности, для чего введём дисбаланс DКОМП с параметрами DКОМП = 25000 г^мм, фазовый угол а^омп = 260°, компенсирующий действие начального дисбаланса DНАЧ в верхней плоскости коррекции. В нижней плоскости коррекции появится дополнительный дисбаланс DДПЛ1 , значение которого в соответствии с (3) составит DДПЛ1 = 7500 г·мм, а фазовый угол βДПЛ1 = 80°. Дисбаланс DДПЛ1 в сумме с дисбалансом DНАЧ в соответствии с (4) и (5) сформирует в нижней плоскости коррекции дисбаланс DКОМП с параметрами: D КОМП = 16707 г·мм, фазовый угол βКОМП = 97,5°. Откуда поперечное смещение центра масс ЛМ в соответствии с выражением (6) составит ρКОМП = 0,167 мм, что превышает заданное значение ρ несмотря на наличие перекоса продольной ГЦОИ также.

Используя (7), рассчитаем параметры корректирующего дисбаланса D^КОРР , действие которого в верхней плоскости коррекции позволит устранить перекос продольной ГЦОИ относительно геометрической оси контролируемой летающей модели: D ^КОРР = 12851,5 г·мм, фазовый угол α ^КОРР = 97,5°. При этом в нижней плоскости коррекции, согласно (8), сформируется новый дополнительный вектор дисбаланса D^{ДПЛ 2} , обусловленный взаимовлиянием плоскостей коррекции с параметрами: D ^{ДПЛ 2} = 3855,5 г·мм, фазовый угол

β ^{ДПЛ 2} = 277,5°. Это, в свою очередь, плоскости коррекции дисбаланса D^КОРР β ^КОРР = 97,5°.

в соответствии

с параметрами:

с (9), вызовет появление в нижней D ^КОРР = 12851,5 г·мм, фазовый угол

Для условия α ^КОРР = 0, вытекающего из равенства значений сонаправленных векторов дисбалансов D^КОРР и D^КОРР , предполагаемое поперечное смещение центра масс с геометрической оси ЛМ в соответствии с выражением (10) составит значение ρ ^КОРР = 0,257 мм, что превышает заданное предельно допустимое значение ρ .

С использованием выражения (14) рассчитаем минимальный угол перекоса продольной ГЦОИ α , не превышающий значения α , при котором для данной конструкции ЛМ возможно обеспечить величину поперечного смещения центра масс, равную ρ . В результате расчёта получим: α = –8,5 ' , т. е. неравенство α ≤ α окажется верным. При этом знак «минус» говорит о наклоне продольной ГЦОИ верхним концом в сторону геометрической оси ЛМ.

Определим значение вектора дисбаланса D^КОРР в плоскости коррекции В , обеспечивающего достижение значения α , по формуле (15). Получим: D^КОРР = 9581,4 г·мм, фазовый угол α ^КОРР = 277,5°. Значение сонаправленного дисбалансу D^КОМП дисбаланса D^КОРР определим по формуле (16): D^КОРР = 19581,4 г·мм, фазовый угол β ^КОРР = 97,5°. При этом значение дополнительного дисбаланса D^{ДПЛ 3} , противоположно направленного по отношению к дисбалансу D^КОРР , будет определяться выражением (17): D ^{ДПЛ 3} = 2874,4 г·мм, фазовый угол β Н ^{ДПЛ 3} = 97,5°.

Используя соответствующие параметры смоделированных векторов дисбалансов D^КОРР и D^КОМП , определим значение и угловое положение вектора балансировочного дисбаланса D^БАЛ в штатной плоскости коррекции по формулам (18) и (19): D^БАЛ  = 34259,3 г·мм, фазовый угол

В | α ГЛмин

α ^БАЛ   = 268,75°.

В | α ГЛмин

В соответствии с (20), масса балансировочного груза составит m^БАЛ   = 171,3 г, а угол его

В|αГЛмин установки ϕБАЛ   в плоскости коррекции В будет совпадать с углом αБАЛ  , т. е. будет равным

268,75°.

Для оценки правильности работы рассмотренного алгоритма, убедимся, что предполагаемое значение смещения центра масс ρ ^РАСЧ после прикрепления к ЛМ груза m^БАЛ   составит

|αГЛмин                                                                    В|αГЛмин величину, близкую к ρ .

Значение дисбаланса D^БАЛ (на рисунке не показан), противоположно направленного дисбалансу α ^БАЛ , появляющемуся взамен дисбалансам D ^{ДПЛ 1} и D ^{ДПЛ 3} в плоскости коррекции Н как результат действия дисбаланса D^БАЛ , может быть определено по формуле

БАЛ       БАЛ

^{DН | α} ГЛмин ^{= DВ | α} ГЛмин ^{КНВ .}

Таким образом, D^БАЛ  = 10498,8 г·мм, фазовый угол β ^БАЛ   = 88,75°. Расчётное значение

Н|αГЛмин                                                       Н |αГЛмин смещения центра масс ЛМ, пренебрегая (как несущественно малой) массой балансировочного груза, определим по формуле

РАСЧ ρ | α ГЛмин

НАЧ    НАЧ    БАЛ       БАЛ

^{DВ   + DН   + DВ | α} ГЛмин ^{+ DН | α} ГЛмин

.

M

Получим ρ ^РАСЧ = 0,11 мм, что практически соответствует заданному значению ρ .

Таким образом, в результате расчёта, проведённого по предложенному алгоритму, найдены искомые параметры балансировочного груза, установка которого обеспечивает выполнение условия (23) с минимально возможным для данной ЛМ отклонением продольной ГЦОИ от её геометрической оси. Подтверждена хорошая согласованность расчётных данных, что доказывает верность проведённого балансировочного расчёта.

Заключение. Рассмотренный алгоритм балансировки конической летающей модели в динамическом режиме с использованием единственной плоскости коррекции, конструктивно расположенной на значительном расстоянии от центра масс модели, с оптимизацией по критерию достижения минимального угла перекоса продольной ГЦОИ, дополняет алгоритм [1 ; 2; 12]. Алгоритм был экспериментально опробован с положительными результатами на вновь спроектированном вертикальном динамическом балансировочном стенде с газовыми опорами и защищён патентом РФ № 2694142 [18]. Проводится работа по внедрению алгоритма в методику балансировки ЛМ. Алгоритм позволяет сократить число шагов балансировки (как правило, до одного шага) либо расчётным путём доказать невозможность балансировки ЛМ с заданными параметрами и, соответственно, сократить время проведения балансировочного эксперимента.