К вопросу снижения энергозатрат в процессе обогащения песков

В условиях, когда отсутствует контроль качества песка – одного из основных компонентов бетонов и растворных смесей – и множества фактов разрушения бетонных и железобетонных конструкций с тяжелыми последствиями, необходимость разработки технологии обогащения песка становится очевидной. Доминирующим условием производства обогащенного песка является его низкая себестоимость. При этом поставщик песка стремится к максимально возможной прибыли, а потребитель желает приобрести его по возможно низкой цене, что приводит к трудно преодолимому препятствию в условиях рыночной экономики.

В представленной работе авторы рассматривают возможность обогащения песка с использованием эффекта расслоения по крупности по высоте сужающегося гидротранспортного лотка. Первоначальное подтверждение возможности использования этого эффекта было получено в экспериментах в производственных условиях [1], основанных на теоретических представлениях и экспериментальных данных [2, 3].

В качестве лотка для проведения экспериментов использовалась сливная труба мелкого продукта конического грохота (КГ) диаметром 500 мм с открытым верхом и наклонная по ходу истечения пульпы на 18°. В нижней части трубы в особых гнездах подвижно были установлены пробоотборные трубки диаметром 36 мм, первая из которых на расстоянии ≈ 5 м от конусного грунтосборника, а вторая и третья – соответственно на расстояниях 200 мм между ними. Этим достигалась относительная стабилизация течения пульпы и возможность расслоения песка по крупности по глубине потока hп, а так же снижения эффекта возмущения течения пульпы у приемного зева пробоотборных трубок при обтекании впереди стоящих (см. рис. 1).

Открытый верх трубы использовался для контрольного отбора и анализа проб, отобранных специальным прибором типа батометра.

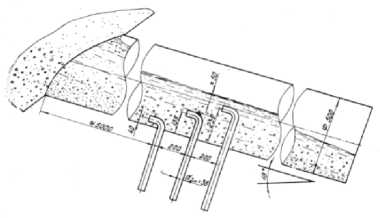
Рис. 1. Схема отбора проб гидросмеси мелкого продукта на коническом грохоте

Одновременный отбор проб в тарированные ёмкости с контролем времени отбора позволял определить одновременно три важных параметра:

• – расход отбираемой пробы

Qср=Ʋср Wсм.с, где Qср – объёмный расход пульпы в каждом эксперименте, м3/с; Wсм.с – площадь смоченного сечения лотка по оси средней пробоотборной трубки;

• и = —

• и ср ₃ ,

где в свою очередь Ʋ ί – скорость входа пульпы в зев каждой пробоотборной трубки;

– средневзвешенную крупность d _{ср. ί} песка в отобранной пробе;

– суммарное содержание частиц крупностью менее 0,15 мм в исходном песке.

Результаты экспериментов переработаны и сгруппированы по однородным расходам с целью более чёткого представления графиков функций (табл. 1 и рис. 2–5)

di    / h )    Pi    Г h )

——= f   - и —=ф i .

d ср.-   4 h п )   Р исх     I h n )

Здесь d_i – средневзвешенный диаметр песка в каждой отобранной пробе; d _{ср. i} – осреднённый диаметр песка по трём пробам; h_i – ордината оси зева пробоотборных трубок; h _п – ордината смоченного сечения потока пульпы в лотке по оси средней пробоотборной трубки.

Аналогично: p i - содержание частиц менее 0,15 мм в каждой отобранной пробе песка; Р _исх — осреднённое по всему сечению потока.

Точность экспериментов в производственных условиях недостаточна, но и они дают общее представление об основных закономерностях обогащения песка в открытых лотках с самотечным гидротранспортом пульпы – ниже они изложены по степени их влияния на качество обогащения.

Прежде чем перейти к основным выводам по результатам натурных экспериментов следует оговорить техническую сторону условий проведения исследований:

– достаточно большой уклон лотка (сливной трубы КГ) – 18° – принят из условий возможного попадания частиц гравия крупностью 5–20 мм в мелкий продукт КГ по причинам неправильного выбора размера межколосниковой щели (в особенности – в коническом сите), износа колосников, ориентирования колосников в секциях сита cпутно потоку пульпы и т. п., что значительно сокращает время расслоения песка по крупности по высоте потока;

– круглое поперечное сечение заведомо проигрывает прямоугольному, так как высота участка (глубина) потока, на котором происходит расслоение частиц песка по крупности, неодинакова по ширине (диаметру) лотка.

Анализ данных табл. 1 и графиков на рис. 2–5 позволяет высказать следующее:

– средневзвешенный диаметр частиц песка в отобранных пробах по мере приближения отборника к поверхности потока пульпы в лотке снижа-

Таблица 1

Результаты экспериментов отбора проб гидросмеси мелкого продукта на коническом грохоте

№ опыта	Q ср , м3/с	d ср , мм	β исх , %	dί / d ср при hί / h п		β ί / β исх при h ί / h п
				0,1	0,7	0,1	0,7
1	2	3	4	5	6	7	8
1	0,383	1,21	4,83	1,43	0,64	0,75	1,14
11	0,352	1,21	5,51	1,20	0,60	0,30	1,64
12	0,374	0,72	4,59	1,26	0,60	0,71	1,24
2	0,475	1,11	3,60	1,24	0,74	0,64	1,25
5	0,499	1,15	4,17	1,60	0,60	0,68	1,29
9	0,445	1,25	3,80	1,61	0,57	0,64	1,34
10	0,494	1,83	2,77	1,61	0,36	0,53	1,55
3	0,452	0,88	8,43	1,26	0,57	0,31	1,64
4	0,413	0,68	11,30	1,51	0,64	0,39	1,51
6	0,417	0,91	6,21	1,23	0,62	0,79	1,21
7	0,447	0,93	6,39	1,48	0,76	0,50	1,38
8	0,465	1,13	7,70	1,20	0,55	0,70	1,25

Примечание: Колонки 5, 6, 7 и 8 рассчитаны по графикам зависимостей d_ί / d _ср = ƒ( h_ί / h _п) и β_ί /β _исх = φ( h_ί / h _п).

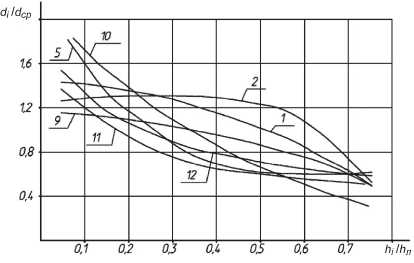
Рис. 2. Зависимость относительной крупности песка d ср от уровня отбора проб в лотке (опыты 1, 2, 5, 9, 10, 11 и 12)

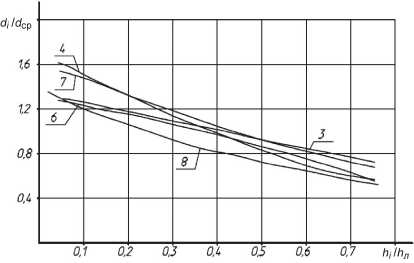
Рис. 3. Зависимость относительной крупности песка d ср от уровня отбора проб в лотке (опыты 3, 4, 6, 7 и 8)

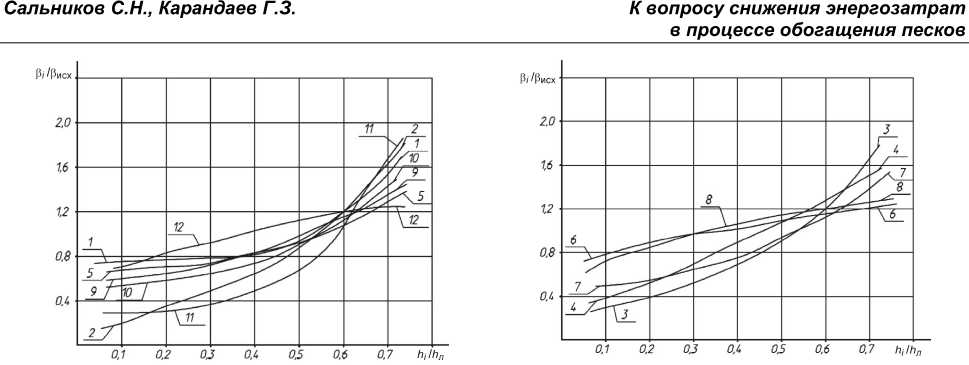
Рис. 4. Зависимость относительного содержания частиц мельче 0,15 мм в пробах песка от изменения уровня отбора проб (опыты 1, 2, 5, 9, 10, 11 и 12)

Рис. 5. Зависимость относительного содержания частиц мельче 0,15 мм в пробах песка от изменения уровня отбора проб (опыты 3, 4, 6, 7 и 8)

ется в 4,47 раза (опыт 10), а выход частиц мельче 0,15 мм возрастает до 5,29 раза (опыт 3);

– чем больше величина d _ср песка в исходной пульпе (мелкий продукт КГ), а также чем меньше содержание частиц менее 0,15 мм в нем, тем больше выход их в поверхностные слои потока пульпы (опыты 1, 2, 10 и 11);

– при уменьшении d _ср исходного песка относительный выход частиц менее 0,15 мм в поверхностные слои потока пульпы в лотке уменьшается (опыты 11 и 12), с увеличением содержания частиц менее 0,15 мм при равном диаметре d _ср исследуемых песков выход их в поверхностные слои увеличивается (опыт 3 и 4);

– с уменьшением расхода пульпы мелкого продукта КГ с естественным снижением её скорости течения в лотке выход частиц менее 0,15 мм в поверхностные слои увеличивается (см. опыты 1,11 и 12), так же как увеличивается время нахождения пульпы на мерной базе лотка, т. е. увеличивается вероятность выхода фракций – 0,15 мм в слив;

– наблюдаемое увеличение глубины (толщины) потока пульпы в лотке при увеличении её расхода несомненно способствует лучшему расслоению частиц песка по крупности;

– прямоугольное сечение лотка также, несомненно, будет способствовать большей эффективности расслоения частиц песка по крупности, так как путь восхождения мелких частиц в верхние слои потока пульпы в каждом поперечном сечении постоянный по ширине лотка. Это важное обстоятельство убедительно подтверждено как теоретически [2], так и практически работами А.И. Куприна [4, 5];

– в заключении анализа результатов натурных исследованиях процессов обогащения песка по крупности в открытом лотке круглого сечения, несмотря на недостаточную точность экспериментов, следует отметить важность выявленных закономерностей процессов и достаточную убедитель- ность полученных графических представлений (см. рис. 3–5).

Расслоение песка по крупности при самотечном гидротранспорте пульпы в лотке может происходить под воздействием двух факторов – разности скоростей осаждения частиц песка различной крупности и восходящей скорости воды, вытесняемой с придонной зоны лотка осаждаемыми частицами. Последний фактор малозначим. Ориентированием процесса обогащения песка только за счёт разности скоростей осаждения частиц также нельзя обеспечить требуемую эффективность по следующим причинам:

– осреднённая по поперечному сечению лотка скорость течения пульпы Ʋср не может быть менее Ʋкр, так как при критической скорости начинается процесс выпадения крупных частиц в осадок, тогда как расслоение песка по крупности возможно только во взвешенном его состоянии;

– с увеличением размера частиц песка и, естественно, скорости их осаждения, возрастает число Рейнольдса Re и неизменный спутник этого явления – турбулентность, снижающая эффективность расслоения [6];

Отсюда вытекают важные следствия:

– для снижения турбулентности в потоке пульпы скорость её течения в лотке должна приниматься по простой зависимости Ʋ_ср = k ·Ʋ_кр, где Ʋ кр – критическая скорость гидротранспорта, соответствующая максимальной крупности песка d mах = 5 мм, k – некий коэффициент запаса, учитывающий возможные нарушения гидравлического режима течения пульпы в лотке;

– уклон днища лотка должен приниматься по условию обеспечения самотечного гидротранспорта пульпы по условию Ʋ_ср = k ·Ʋ_кр.

В горнорудной промышленности широко используются конически сходящиеся лотки для обогащения рудного сырья с разной плотностью минеральных составляющих [7].

С целью проверки возможности совершенствования технологии обогащения песка с моно- плотностью минеральной составляющей с использованием эффекта создания принудительного восхождения пульпы за счёт уменьшения ширины лотка по мере приближения к его разгрузочному сечению, были проведены эксперименты на лабораторном стенде, технологическая схема которого представлена на рис. 6.

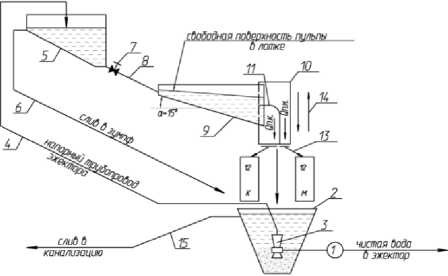
Рис. 6. Технологическая схема стенда для изучения процессов обогащения песка в конически сужающемся лотке

Работа стенда происходит в следующей последовательности:

– в грунтовую ёмкость (зумпф) 2 засыпается исследуемый грунт и устанавливается эжектор 3 с возможностью перемещения по вертикали. Затем насосом 1 вода подаётся на эжектирование в эжектор 3.

Всасываемая пульпа по напорному трубопро- воду 4 подаётся в расходный бак 5. Постоянство уровня воды в зумпфе поддерживается подачей чистой воды из водопровода и сливом её избытка в канализацию по трубопроводу 15;

– расходный бак 5 служит для поддержания статического напора пульпы в лоток 9 и возврата избытка пульпы через трубопровод 6 в зумпф 2. Расход пульпы на лоток 9 регулируется задвижкой 7, от которой веерным лотком 8 вводится в сужающийся лоток 9 по всей ширине его приёмного зева;

– в разгрузочном сечении лотка 9 монтировано пробоотборное устройство 10 с отсекателем 11 для отбора проб крупного и мелкого продуктов в тарированные ёмкости 12 посредством гибких шлангов 13, работающих синхронно – в зумпф, в пробоотборные ёмкости 12 – посредством привода от магнитного тормоза с фиксированием времени отбора проб.

Устройство 10 с механизмом передвижения по вертикали 14 позволяло тонко регулировать толщину «срезаемого» слоя осветлённой пульпы;

– пробы пульпы крупного и мелкого продуктов после отстоя и сушки обрабатывались стандартным способом.

Результаты экспериментов представлены в табл. 2 и на рис. 7. Из табл. 2 видно, что эксперименты велись на песчаных смесях со средневзвешенной крупностью 0,40< d _ср<0,82 мм (опыты 1, 2 и 19), т. е. отношение d_ср ^max / d_ср ^min = 2,05 – достаточно широкий размах колебаний фракционного состава песка.

Таблица 2

Результаты экспериментов на песчаных смесях в процессе обогащения песка в конически сужающемся лотке

№ опыта	Средневзвешенный диаметр песка, d ср, мм	Граничное зерно разделения, d гр, мм	Модули крупности песка – исходного и продуктов разделения
			м „ к.исх	М к.к	М к.м
1	0,40	0,40	1,57	1,72	1,38
2	0,40	0,37	1,60	1,70	1,42
3	0,48	0,42	1,69	1,82	1,50
4	0,52	0,29	1,85	2,11	1,62
5	0,53	0,34	1,86	2,11	1,60
6	0,54	0,32	1,89	2,19	1,64
7	0,54	0,58	1,89	2,10	1,53
8	0,60	0,56	1,99	2,18	1,68
9	0,54	0,23	1,90	2,29	1,59
10	0,58	0,44	2,00	2,24	1,74
11	0,64	0,23	1,90	2,29	1,59
12	0,60	0,48	2,06	2,38	1,57
13	0,65	0,75	2,11	2,29	1,67
14	0,62	0,33	2,12	2,40	1,88
15	0,64	0,41	2,12	2,37	1,80
16	0,66	0,43	2,12	2,44	1,61
17	0,80	0,35	2,16	2,44	1,93
18	0,70	1,20	2,18	2,40	1,78
19	0,82	1,50	2,40	2,56	1,89
20	0,57	0,54	1,95	2,10	1,65
21	0,65	0,41	2,25	2,46	2,09
22	0,57	0,35	1,97	2,26	1,63

Сальников С.Н., Карандаев Г.З.

На этих песках разделение на крупный и мелкий продукты происходило при изменении граничного зерна в пределах 0,23< d гр <1,50 мм (опыты 9, 11 и 19). Отношение d гр^max / d гр^min = 6,5 – также убедительный размах экспериментальных материалов для определения основных законов процессов обогащения песка в сужающихся лотках.

Зерновой состав обогащаемого песка и продуктов обогащения контролировался также показателями их модуля крупности:

М_к.исх – исходного песка; М_к.к – крупного продукта; М к.м – мелкого продукта.

Диапазон колебаний этих показателей изменялся в следующих пределах:

1,57 ≤ Мк.исх ≤ 2,40 (опыты 1, 19);

1,7 ≤ М к.к ≤ 2,56 и 1,38 ≤ М к.м ≤ 2,09.

Результаты экспериментов представлены на рис. 7 в виде графиков зависимостей М к.к = ƒ(М к.исх ) и М_к.м = φ (М_к.исх), рассмотрение которых позволяют заключить, что зависимости М_к.к и М_к.м от М_к.исх линейны и могут быть представлены уравнением y=a+bx решаемым способом избранных точек [7] путём составления вспомогательной табл. 3 по

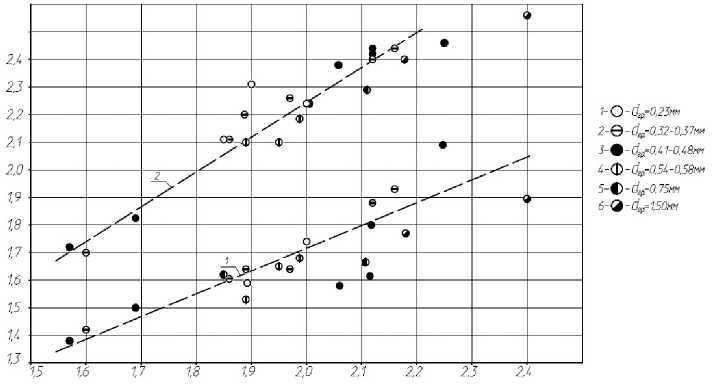
Рис. 7. Графики зависимости М к.к = ƒ (М к.исх ) и М к.м = φ (М к.исх ) при переменном граничном зерне разделения d гр песка

Таблица 3

Проверка точности результатов

№ п/п	М к.исх ( х ί )	x ί ²	М к.м ( y ί )	xίyί	М к.м расчетн.	Ошибка, %
1	1,6	2,56	1,38	2,21	1,38	–
2	1,7	2,89	1,47	2,50	1,47	–
3	1,8	3,24	1,55	2,79	1,56	0,64
4	1,9	3,61	1,63	3,10	1,64	0,61
5	2,0	4,00	1,72	3,44	1,73	0,58
6	2,1	4,41	1,80	3,78	1,82	1,10
7	2,2	4,84	1,88	4,14	1,90	1,06
7 2 1	13,3	25,55	11,43	21,96	–	–
№ п/п	М к.исх (х ί )	x ί ²	М к.к ( z ί )	x ί z ί	М к.к расчетн.	Ошибка, %
1	1,6	2,56	1,74	2,78	1,92	10,34
2	1,7	2,89	1,87	3,18	2,02	8,02
3	1,8	3,24	1,98	3,56	2,13	7,57
4	1,9	3,61	2,12	4,03	2,23	5,19
5	2,0	4,00	2,24	4,48	2,34	4,46
6	2,1	4,41	2,37	4,98	2,44	2,95
7	2,2	4,84	2,50	5,50	2,55	2,24
7 2 1	13,3	25,55	14,85	28,51	–	–

«сглаженным» точкам графиков на рис. 7 и равноотстоящих координат абсцисс в пределах

1,6 ≤ М к.исх ≤ 2,2.

Параметры уравнения определены по зависимостям:

a =

∑ x ² ∑ y - ∑ x ∑ xy

n ∑ x ² - ( ∑ x )²

; b =

n ∑ xy - ∑ x ∑ y

n ∑ x ² - ( ∑ x )²

Здесь n =7 – число равноотстоящих значений x ί = M к.исх (см. табл. 3); y ί = M ^ίк.м – значения модуля крупности мелкого продукта по «сглаженной» прямой функции М к.м = φ (М к.исх ).

Расчёты по вспомогательной табл. 3 позволи- ли определить параметры уравненияy=a+bx: а=0,1 и b=0,87 – для функции Мк.м = a+bx; а=0,24 и b=1,05 – для функции Мк.к = a+bx.

Расчётные формулы в окончательном виде представлены ниже:

М к.м = –0,1 + 0,87 М к.исх;                     (1)

М к.к = 0,24 + 1,05 М к.исх .                      (2)

Соответствие расчётных величин М к.м и М к.к фактическим (по «сглаженным» графикам на рис. 7) представлено в колонке 7 табл. 3.

Ошибки составляют:

для мелкого продукта – от 0,0 до 1,1 %;

для крупного продукта – от 2,2 до 10,34 %.

Отклонения расчётных точек значений Мк.к и Мк.м, соответствующим тем же значениям на графиках рис. 7 в тех же координатах абсциссы (Мк.исх), находятся в основном в пределах точности экспериментов – за исключением графика функции Мк.к = ƒ (Мк.исх), где явно просматривается недостаточность экспериментов по обогащению песка с малыми значениями Мк.исх. Однако, полагаясь на сложность гидравлических процессов разделения песка по фракциям в сужающихся лотках и невозможность учета всех взаимовлияющих факторов (на данном уровне теоретических представлений), эти ошибки следует считать приемлемыми.

Практическое использование полученных результатов сводится к следующему:

– имея геологоразведочные данные по зерновому составу карьерного песка можно определить, в зависимости от требований потребителей, необходимый режим обогащения: фракционирование и удаление частиц крупностью – 0,15(0,16) мм, или же только обогащение с удалением частиц – 0,15(0,16) мм и части фракции 0,31–0,15(0,16) мм – при необходимости;

– определения величины возможного приращения модулей крупности фракционированного и обогащённого песков при известном модуле крупности исходного по формулам (1) и (2);

– определение возможной технологии складирования фракционированного (обогащённого) песка в зависимости от объёма отбираемой пульпы с некондиционными фракциями песка.

Кроме того, результаты исследований позволяют разработать рекомендации для проектирова- ния более совершенного конически сходящегося лотка, суть которых сводится к следующему:

– процесс расслоения частиц песка по глубине потока пульпы в лотке следует основывать на эффекте увеличения глубины по мере сужения лотка по ходу движения к его сливному сечению. При этом: скорость подъёма уровня пульпы в лотке должна быть согласована с величинами гидравлической крупности некондиционных фракций песка, подлежащих удалению в хвостохранилище; угол конусности лотка α° должен быть таким, чтобы воспрепятствовать возникновению мощных поперечных турбулентных течений в лотке, неизбежно вызывающих поперечную флуктуацию частиц песка, снижающих эффективность расслоения. Целесообразно использовать рекомендации [8/ для выбора оптимальных параметров лотка, применительно к теории конфузора;

– так как крупные частицы (гравий) могут вызвать достаточно мощные турбулентные возмущения и даже грядообразование на днище лотка, вызывающее восходящие потоки, снижающие эффективность расслоения, то необходимо соблюсти два условия: из исходной пульпы перед подачей её в конически сходящийся лоток должны быть удалены все частицы крупностью + 5 мм и органические включения; скорость движения пульпы по лотку, выбираемая по условию Ʋ = k Ʋ_кр (см. выше), должна быть такой, чтобы гарантировано обеспечить гидротранспорт песка во взвешенном состоянии, поэтому величина коэффициента k должна быть обоснована на экспериментальных материалах по гидротранспорту;

– концентрация песка в пульпе неконтролируема, так как она зависит от режима работы гидротранспортной системы земснаряда, поэтому величина коэффициента k должна учитывать и это обстоятельство;

– форма сужающегося лотка должна быть прямоугольна в сечении, так как при такой форме скорость течения пульпы на входе в лоток по всей ширине лотка относительно постоянна в каждый отрезок времени так же, как концентрация твёрдого в пульпе и, кроме того, глубина потока пульпы в лотке хотя и переменна по его длине, но постоянна в сечениях, что, в совокупности, создаёт наилучшие условия для процесса расслоения песка;

– складирование обогащённого песка возможно намывом при уменьшенном эффекте сегрегации песка по крупности за счёт сброса в хвосто-хранилище пульпы с частицами крупностью – 0,15 (0,30) мм. Складирование фракционированного песка возможно только комбинированным способом: крупный продукт – механически, мелкий – намывом;

– в работе авторов данной статьи [8] обоснована необходимость проектирования мобильных обогатительных установок, поэтому предлагаемая технология обогащения песков должна быть в мобильном варианте по блочной схеме: добычной

Сальников С.Н., Карандаев Г.З.

агрегат (земснаряд) – отбор гравия и его складирование – обогащение песка и его складирование – хвостохранилище.