К вопросу установления коэффициентов безопасности и запасов прочности при заданной вероятности неразрушения силовых конструкций

Введение. Коэффициент безопасности, согласно ГОСТ Р 56514–2015, учитывает неточность теоретического и экспериментального определения нагрузок и несущей способности, а также случайный разброс этих нагрузок, а запас прочности – избыток природной прочности материала по сравнению с необходимой для его работы в данных условиях [1]. Таким образом, говоря о коэффициентах безопасности, имеют в виду внешние нагрузки, а запасы прочности принято главным образом использовать для выбора механических характеристик конструкционных материалов.

В детерминированной постановке задач прочности коэффициент безопасности f используют для определения расчетной нагрузки N^P

NP = f ∙ N, где N – эксплуатационная (действующая) нагрузка.

Под N понимают значение нагрузки и режим нагружения (зависимость нагрузок от времени), реализуемые в рассматриваемом случае нагружения в процессе эксплуатации.

Запас прочности элемента конструкции определяют по формуле ст

_ ' пред                 _ ° пред

П^- п , или П^- —р->

NP              о P где Nпред - величина предельной нагрузки; апред - предельное напряжение; aP - эквивалентное расчетное напряжение.

Если рассматривать прочность в категории внутренних усилий конструкции, то для простейших сочетаний типов конструктивных элементов и нагрузок, несущая способность R , в виде неразрушающих внутренних нагрузок, равна

R -

о ( N ) X

пред

- П - f • N,

где a( N) - максимально допустимые локальные напряжения, возникшие от нагрузки N , Па; X - коэффициент, зависящий от размеров поперечного сечения конструктивных элементов.

Значение a(N) зависит от действующих нагрузок, например, при сложном напряжённом состоянии (одновременно ненулевые нормальные и касательные напряжения) используют один из четырёх критериев предельного напряжённо-деформированного состояния (механической теории прочности) [2]. В свою очередь X зависит от размеров поперечного сечения конструктивных элементов [3]. Например, для растягиваемого стержня х-F для изгибаемого стержня

д а-lх - —,

WZ для скручиваемого стержня

X- —

WK где F - площадь поперечного сечения; а - коэффициент, зависящий от условий закрепления балки и нагрузки; l - длина стержня; WZ - момент сопротивления сечения стержня при изгибе; WK - момент сопротивления сечения стержня при кручении.

При нормальном распределении R и N (знак функциональной зависимости от времени здесь и далее опущен), без учета корреляционной зависимости, вероятность неразрушения элементов конструкции, т. е. вероятность того, что несущая способность R будет больше действующей нагрузки N , определяется как

P - Вер { R >  N } - Ф ( z ) - Ф

m R - m N

L 2 , _2

VV°R + °N J где Ф(z) - функция нормального распределения (функция Лапласа); mR, mN - математические ожидания R и N; aR, aN - среднеквадратические отклонения R и N.

При нормальных законах распределения случайных величин нагрузки и сопротивления модель отказов по схеме «нагрузка - сопротивление» имеет следующий вид (рис. 1).

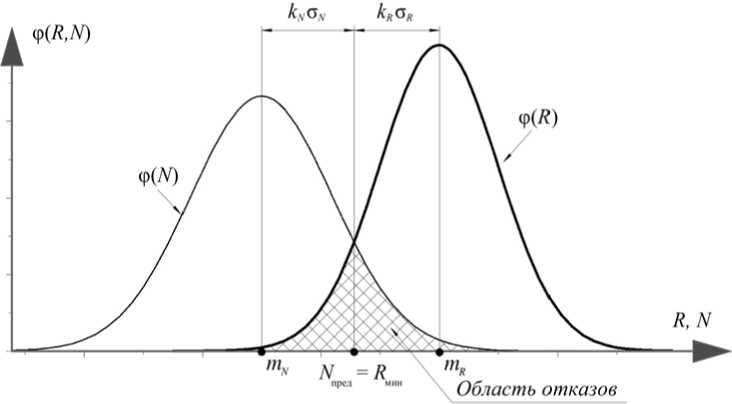
Рис. 1. Модель отказов по схеме «нагрузка – сопротивление» при нормальном законе случайных величин

Fig. 1. Model of failure on the scheme “load – resistance” by the law of normal distribution random variable

Как следует из рис. 1, максимальная вероятность неразрушения элементов конструкции достигается разделением средних значений m_R до m_N , а также снижением σ _R и/ или σ _N. При этом минимальная несущая способность и предельная нагрузка всегда лежат в диапазоне от m R до m N и при условии z > 0 определяются выражениями

R _мин = m R – k R ∙ σ R ,

Nпред = mN + kN ∙ σN, где kR, kN – числовые коэффициенты, характеризующие вероятность отклонения случайной величины от математического ожидания, которые для высоконадежных систем устанавливают- ся от 3 до 6 (исходя из правил трех сигм или шести сигм) [4]. Случай, когда

R мин

= N пред ,

при любом способе повышения надежности определяет минимальную область отказов (см. рис. 1).

С учетом выражений (1)–(5) получаем n = Rмин ,                                           (6)

N пред где n – обобщенный коэффициент безотказности и запаса прочности, одновременно учитывающий действующие нагрузки и характеристики конструкционного материала, который равен n = η ∙ f.

Математические ожидания в выражении (2), при условии выражения (5) (в точке пересечения кривых плотностей распределения согласно рис. 1) с учетом (1), (3)–(6) можно определить зависимостями mR =  Rмин

1-k ⋅υ

RR

n ^⋅ N пред 1 - k_R ⋅υ _R ,

N пред

mN = 1         ’

1 + kN'uN где υR, υN – коэффициенты вариации несущей способности (прочности) и нагрузок.

Значения υ R , υ N определяются по формулам

^R-u R =    , mR

°N ^u N = ^N .

mN

Среднеквадратические отклонения в выражении (2) с учетом (7)–(8) можно представить как

^C R

= ^u R

n ' ^U R • ^Nпред

^{1 -} k R ' ^U R

^U N

= ^u N

• mN =

^u N ' ^N пред

¹ + k_N •u _N

С учетом (7)–(10) выражение (2) для наиболее нагруженного элемента конструкции принимает вид

P = ф

n ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^™   •

^{1 — k}R ' ^U R

^^^^^^^

N U N

.

n •U R

R

^U N k N ' ^U N

С учетом правила трех сигм формулу (11) можно записать в виде [5; 6]

n

^^^^^^B

P = ф

1 — 3 • u r 1 + 3 • u

n •U R

R

^U N

1 + 3 •U

.

Допустим, что u _R = u _N = 10 % [5]. Тогда при обобщенном запасе прочности n = 1,5 (например, при f = 1,5 и η = 1,0) значение нормированной случайной величины составляет = 6,03, что соответствует вероятности неразрушения конструкции более 0,999999999 [7].

Использование формул (11)–(12) дает возможность с помощью коэффициентов безопасности и запасов прочности управлять прочностной надежностью конструкции на этапе проектирования.

Коэффициенты безопасности f , как правило, отражают отраслевую специфику подходов и методов обработки статистической информации о нагрузках, отраженных в частных нормах прочности с учетом полноты и точности информации о величинах и повторяемости эксплуатационных нагрузок, а также объема экспериментальной отработки, точности воспроизведения режимов нагружения при испытаниях. В частности, для силовых конструкций автоматических космических аппаратов могут быть использованы рекомендуемые коэффициенты безопасности по ГОСТ Р 56514–2015, которые, как правило, принимают равными от 1,3 до 1,5, но в отдельных случаях, могут достигать значений 2,0÷2,6.

Запасы прочности η принято назначать исходя из значений коэффициентов вариации для сталей υ R = 5–9 % и для алюминиевых сплавов υ R = 4–6 % [8; 9], что соответствует приемлемости вычислений по формуле (12). Однако такой подход учитывает только природную прочность материала, без учета вариации геометрических характеристик конструкции, влияющих на величину сопротивления конструкции внешним нагрузкам [2]. В то же время известно, что значения коэффициентов запаса прочности неразрывно связаны с закладываемыми в расчеты допущениями и потому требуют точной формулировки используемых методов расчета, требований к точности исходных данных и т. п. [10].

Пример. Рассмотрим влияние разбросов геометрических размеров поперечного сечения конструктивного элемента на запас прочности на примере антенны, консольно закрепленной на борту КА, показанной на рис. 2, на которую действуют поперечные перегрузки n x активного участка полета. Тело антенны выполнено из изотропного материала с пределом прочности [σ] = 140∙10⁶ Па. Антенна имеет постоянное сечение в виде круглой трубы D = (65,5 ±0,3) 10^–3 м и d = (64,1±0,4) 10^-3 м. Масса антенны m равномерно распределена по длине L .

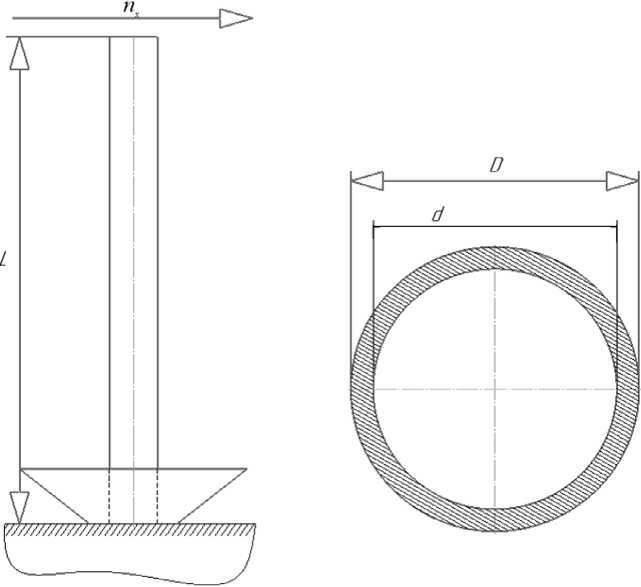
Q                              б

Рис. 2. Схема закрепления ( а ) и сечение антенны ( б )

Fig. 2. Schematics attachment ( a ) and cross-section of antenna ( b )

Внешняя распределенная нагрузка на антенну q N равна

Г m • g q N = f • n x • —,                                   (13)

где g – ускорение свободного падения.

Изгибающие моменты в антенне равны

M n = qN-^L²- ,                                  (14)

Из формул (13)-(14) видно, что изгибающие моменты, действующие на антенну, определяются некими внешними факторами условий эксплуатации, которые выражены через n x и в некоторой степени характеризуются свойствами реальной конструкции (в рассматриваемом случае - это масса m и длина консоли L ), которые определяют (влияют на) величину внешних нагрузок. Случайный разброс параметров внешних нагрузок, связанный с расхождениями их теоретического и экспериментального определения, учитывается коэффициентом безопасности f. Накопленный в ракетно-космической отрасли опыт [11; 12] позволяет предположить, что при существующих комбинациях условий эксплуатации и принятых конструктивносиловых схем КА, максимальные значения коэффициентов вариации нагрузки не превысят и N = 0,1 [5], и, соответственно, к выбору значений коэффициентов безопасности могут быть приемлемы рекомендации ГОСТ Р 56514-2015.

Теперь рассмотрим внутренние изгибающие моменты M R в сечениях штаги, которые сопротивляются действию внешней нагрузки M N (14):

Mr =

л-о-(D4 -d4)

32 ■ D

где а - нормальное действующее напряжение.

При условии сохранения прочности с учетом (1) имеем

M r ^

п "[с]"( D 4 — d 4)

32 ■ D

С учетом нормального закона распределения случайной величины (2) суммарное среднеквадратические значения сопротивления внешним нагрузкам а R определяются как [13]

О R =

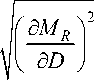
■ ( U d ■ D ) 2 +

M. f

/            \ 2

ЛЛЛ ,

где иD - коэффициент вариаций внешнего диаметра; иd - коэффициент вариаций внутреннего диаметра; U[o] - коэффициент вариаций допустимого напряжения материала. Или, для нагляд- ности, в виде

^О r =

/1 I 2 ~ 2

\ ^О R (1) + ^О R (2) + ^О R (3) .

Исходя из (15), (16) коэффициент вариаций несущей способности иR является функцией, зависимой от иD, иd, U[o]. Зададим для упрощения коэффициент вариации материала, исходя из общепринятой практики расчетов, U[o] = 10 % [5]. Тогда коэффициент вариаций иD для внешнего диаметра D можно вычислить по формуле

^D

U D =-- mD где mD - математическое ожидание размера D (в нашем случае mD = 0,0655 м); аD - среднеквадратическое отклонение D.

Значение а _D можно определить по формуле

1                       х²

^О D =J—y X ( m D - x i ) , V J ¹ i = 1

где x i - все значения параметров измерений в заданном диапазоне; j - количество измерений.

В связи с тем, что существуют жесткие ограничения по предельным размерам, то можно принять j = ∞. Таким образом, формула для вычисления итогового значения коэффициент вариаций и D будет иметь вид

1 j                2

\    ,'Е(mD -ХЛ

V j ¹ г = 1

и D = lim ------------------- jj ^“           m _L

С учетом (17) для размеров D и d были получены следующие значения: и D = 0,26 % и и _d = 0,36 %.

Таким образом, с учетом (15), (16) получаем:

п- [ з ] - D 2     1 п- [ 3 ] - ( D 4 - d 4 ) , х 3 R (1) =        8             -                         '( U d 'D ) , 832   D к                                   7 ' [ з ] -п- d 4 - и d 3 R (2) =        8 - D       ’ к              7 fn- [ 3 ] -u [ 3 ] - ( D 4 - d 4 г 3 R (3) =            32 - D           • к                       7

Для иллюстрации вклада каждого слагаемого на среднеквадратичное отклонение σ R посчитаем последовательно

³ R (1) =

п- 140 - 10⁶ • 0,0655 2

1 п- 140 - 10⁶ • ( 0,0655⁴ - 0,0641 4 ) ^

32             0,0655 2             ^

х ( 0,0026 • 0,0655 ) = 39,34 Н-м,

³ R (2) =

' ( 140 - 10⁶ ) -п- 0,0641 4 • 0,0036 ^

= 51,01 Н-м,

8 • 0,0655

к                               7

³ R (3) =

'п- ( 140 - 10⁶ ) • 0,1 - ( 0,0655⁴ - 0,0641 4 ) 32 • 0,0655

= 31,98 Н-м.

Таким образом,

³ R = V³ R (1) + ³ R (2) ^{+ 3} R (3) = ⁷¹,^{92 Н}^м.

Представленные расчеты показывают, что влияние прочности материала оказывает гораздо меньшее воздействие, чем разброс геометрических характеристик, а суммарный коэффициент вариаций несущей способности будет равен

= 3 R =        3 R       =____________ 71,92 ____________ = 71,92 = 0 225

m R   п- [ з ] - ( D ⁴ - d ⁴)    п- 140 - 10⁶ • ( 0,0655⁴ - 0,0641 4 ) 319,78    ,

32 - D                   32 - 0,0655

Таким образом, учет вариаций геометрических размеров сечения способен увеличить разброс несущей способности конструкции до 2,25 раз. Это приводит к тому, что при υ _N = 10 % и υ R = 22,5 % не существует приемлемых комбинаций коэффициентов безопасности и запасов прочности, которые бы обеспечили неразрушение критичных элементов с вероятностью P = 0,999999999. Согласно формуле (12), в данном случае при обобщенном запасе прочности n = 1,5 может быть достигнута вероятность неразрушения P = Φ(3,69) = 0,99989. Для повышения надежности в данном случае необходимо исключить разброс размеров геометрических сечений, что возможно при расчетах на прочность в запас с учетом минимаксного подхода [14; 15], когда расчет момента сопротивления сечения производится при минимально возможном внешнем диаметре D и максимально возможном внутреннем диаметре d антенны.

Заключение

• 1.    Назначение коэффициентов безопасности и запасов прочности при расчетах на прочность элементов конструкций следует производить, исходя из требуемых показателей надежности изделий.

• 2.    Существует возможность определить математическую зависимость между коэффициентами безопасности, запасами прочности и вероятностью неразрушения элементов конструкции.

• 3.    Коэффициент безопасности определяет величину внешних нагрузок, а запас прочности – внутренних усилий (напряжений).

• 4.    При назначении коэффициентов безопасности и запасов прочности следует учитывать не только вариации нагрузки и физических свойств материалов, но и вариации размеров геометрических сечений, в первую очередь, при расчетах внутренних усилий (напряжений).

• 5.    При использовании тонкостенных конструкций с нерегламентированными полями допусков на размеры сечений расчеты на прочность следует производить, исходя из минимально возможного момента сопротивления сечения, с учетом вариации определяющих его размеров.