К выбору математической модели для корректного решения краевой задачи течения тонкого слоя пластического материала при сжатии образца в виде кругового сектора

v   u v w

|v|    |v| + | v| ^' + |v| ^'

d- - Ou Ov Ow

8x Oy Oz "

Принимая гипотезу о том, что деформированное состояние сжимаемого слоя является плоским, представим систему уравнений системой (3) - (5) [4,6]:

(1) и (2) рассматриваемой краевой задачи, новой

дР _		^Ts	и
дх		j	^u2+v2
дР —		2t s	и
ду		j	^u2+v2
ди + дх	дv ду	—	-—О. dt

;

;

По определению свободная поверхность пластической области имеет криволинейную границу в виде дуги окружности с известным центральным углом, для удобства перейдем к цилиндрической системе координат. Уравнения связи координат двух систем имеют вид [7]:

х — рсозф; у — рз1пф; z — z.

Давление в цилиндрической системе зависит от 3-х координат р — р^р,ф,z^ и его градиент определяется в соответствии с (6):

^{где е}р > ^еф > ^еz

-

дгаа ^р др ^ер ⁺ дф ф ¹ дz^е^                                    ⁽⁶⁾

единичный ортонормированный базис   (полярной системы координат),

связанный с единичным ортонормированным базисом i,j, к стандартными соотношениями, известными из линейной алгебры:

дх .  , ду .  , дz             дх .  ,  ду .  , дz _      дх . , ду . , дz , ео — — I + — j + —к; е(0 — — i + — j + — ;е7 — — i + — j + — к.

р   др    др3   др ф   дф    дф3   дф z   дz дzJ дz

При переходе от декартовой системы координат к цилиндрической системе координат необходимо учесть стандартные преобразования с помощью матрицы Якоби [8]:

/ дх дх др дф

7 =

ду др

ду дф

dz dz

\ др дф

дх\ дz ау дz дz дz)

( С05ф з1"ф

О

^^^^^^^^

рзкпф О\

рсозф О

Определитель матрицы Якоби - Якобиан, в этом случае |/| — р. После использования такого

стандартного перехода вектор скорости примет вид

V — v(U р ,V ф ,W z ) .

В этом случае его дивергенция представляется соотношением diVV—        ■ .".^w.

р др р дф дz или

— ЦАр^У-^. р ^р др ^м др р дф дz

После раскрытия скобок и очевидных преобразований имеем: _d iVV —       . ■ .          .• " ■.

др р р дф дz

Условие несжимаемости так же приобретет новый вид: au p + u p + ia^ + aw , _ dz — о. др р р дф дz dt

Векторное уравнение (6) в явном виде:

др 1 др др _ е0 +    е„ + ег др р р дф ф дz

2t_s и р в р +У ф в ф +W z e z

^u^p+y ф +w Z

Принимая для рассматриваемого течения гипотезу плоского деформированного состояния и осуществив переход к цилиндрической системе координат, перейдем к следующей постановке [6]:

дР —	2ts   и р
др	j Ju P +v v
1 др _	2ts   У ф
р дф	j ^и Р +У Ф

— дир + Up + 1 дуф др р р дф

- — О. dt

Условие (13) описывает условие постоянства объема, записанное в скоростях;

■   ■ - '"(j^

степень накопленной деформации; h - конечная толщина кругового

сектора.

Алгоритм нахождения контактных давлений и силовых параметров для пластической области. Рассмотрим область очага деформации S . Будем считать, что рассматриваемая область имеет вид сектора, ограниченного фиксированным углом 2 ф , и фиксированным линейным размером как показано на рис. 1.

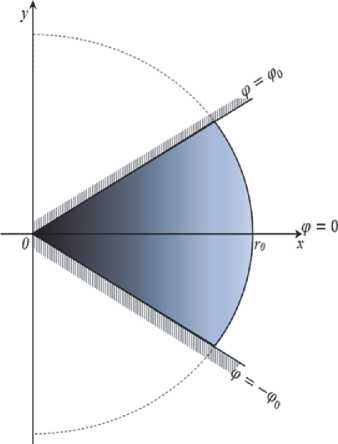
Рис. 1. Схема пластической области S в плоскости Отф в цилиндрической системе координат

Так как рассматриваемая область S симметрична относительно прямой т _ 0 , то можно рассмотреть схему течения металла только в половине области, заданной соотношениями (14)

^У'ф'о ф"ф .                                  (14)

На границе заданной области S компонента скорости очевидно Цр _ 0 (см. рис. 1) и при подстановке нулевого значения в (11) и (13) уравнения преобразуются к виду уравнений первого порядка с разделяющимися переменными

Эр _ _2у 1д^ _ о др h ’ р Эф .

В результате интегрирования первого уравнения, получим оценку давления на контакте: р__^ + С_1;                             (15)

где C - постоянная интегрирования, для нахождения которой используем граничные условия: при т _ т₀,р _ 2t_s :

t^+q. ^s h ¹

Из этого соотношения постоянная интегрирования С₁ :

Г_2г^ _или  Q, _ 2t_s (1 + h ).

Тогда контактное давление в области S .

Если учесть, что значение компоненты скорости Ц р _ 0, то условие несжимаемости (13) будет иметь следующий вид:

au r + У т _ ал _ о ar r dt .

Истинная степень деформации в момент времени деформирования t может быть представлена в виде соотношения (19).

Л _ Л(t) _ Z и ( hot) ) _ ^ ⁿ h₀ _ Znh.

Если продифференцировать по времени соотношение (19) ^ _ ~^^ и подставить результат в (18), то дифференциальное уравнение, выражающее условие несжимаемости будет иметь вид:

au r ₊ У т ₊ 1 dh _ 0 dr г h dt ‘

Для нахождения компоненты радиальной скорости ur соотношение (20) необходимо проинтегрировать. Полученное уравнение является линейным дифференциальным уравнением первого порядка. Это уравнение можно проинтегрировать с помощью метода вариации произвольных постоянных:

1    du_r        1 dh

Л "dr    J hdt~ '

д(гur)      1dh дг       hdt

В результате:

гиг

^u r

г²1 dh

2zhdt + C2

rldh С₂

^-м⁺7 ,

где С₂ - постоянная интегрирования. Постоянная интегрирования может быть определена из граничных условий: при г - 0 скорость u_r - 0 :

0 ₌ -г 2 1^^_{+С2:Сг =} 0.

2 hdt ^{2 2}

Подстановка С₂ в выражение (20) для компоненты скорости приводит к уравнению:

u_r - -^. ^r 2^ at

Разделим переменным и найдем квадратуры (22): к^-ц^.

J r 2 J h

В результате перемещение можно вычислить по формуле (23): U_r - —- inh + inC₃.

Найдем постоянную интегрирования С3. Для этого воспользуемся граничным условием при г - 0 перемещение Ur - 0, тогда 1пС3 - 0. При подстановке значения постоянной интегрирования в уравнение для определения радиального перемещения получим Ur - /(h):

U_r - ^ inh. (24)

Сила штамповки в пластической области S в виде кругового сектора:

^р-2Я₅ prdrdy - 2 Jq⁰ rdr Jq⁰ ^² ^^£ г + 2t_s ^1+ r ^ ^^ dy - ^^^-⁽2г + г₀ + h⁾ . (25)

Таким образом, в рамках общей модели «идеальной жидкости» получено аналитическое решение. На границе ф - ф₀ , а также на свободной границе г - г₀ это решение удовлетворяет граничным условиям в интегральной форме. Следовательно, по принципу Сен-Венана, полученное решение должно быть справедливо в каждой точке области течения.

Для оценки влияния касательных напряжений, осредненных по толщине реального слоя, на кинематику течения, и, что особенно важно, в непосредственной близости от неподвижных границ, были смоделированы и поставлены лабораторные эксперименты по сжатию между сближающимися жесткими плитами тонкого пластического образца, ограниченного неподвижными стенками и, первоначально имеющего форму кругового сектора. Анализ закономерностей, полученных экспериментально, невозможно корректно описать с помощью модели «идеальной жидкости». В реальных экспериментах невозможно пренебречь касательными напряжениями, как это делается в модели «идеальной жидкости».

Для осуществления серии запланированных экспериментов, была изготовлена сменная штамповая оснастка (рис. 2 а) и пары свинцовых пластин (рис. 2) в форме кругового сектора в плане (R₀ - 45 мм; h₀ - 4 мм; ф₀ - 22,5°) .

Для проведения лабораторного эксперимента образец из двух составных пластин устанавливался в канале штамповой оснастки. Пластины осаживались так, что с течением времени центральный угол образца оставался неизменным. Пред началом эксперимента координатная сетка в виде концентрических дуг окружностей наносилась на поверхность одной из двух пластин составной заготовки. Дальнейшее исследование искажения координатной сетки проведены с помощью исследовательского комплекса на базе испытательной машины INSTRON с компьютерной регистрацией параметров рассматриваемого процесса осадки.

Рис. 2. Экспериментальный штамп и заготовки в форме сектора для анализа особенностей стесненной осадки: а - детали штампа; б - образцы! в исходном и деформированном состояниях с нанесенной координатной сеткой

После сжатия измерялось минимальное значение перемещения и_ь = и вблизи неподвижной границы (ф = 22,5°) и максимальное значение и_т = и (R; ф = 0) в средней по ширине точке (у = 0) (см. рис. 1). Измерение координат искаженной сетки проведено на инструментальном микроскопе УИМ-21, оснащенном комплексом компьютерной обработки измеряемых характеристик. Далее была определено абсолютное приращение Дu(R) = и_т - и_ь и относительная величина — ^um отклонения перемещения в сечении R = const . Полученные данные были занесены в табл. 1.

Таблица 1. Перемещения в сечении R = const; h_x = 2,32 мм; Дh₁ = h₀ - h_x = 1,68 мм; — = 0,42; F =164 кН ^ 0 _____

R	U m (R)	Ub(R)	Дu(R) = um — иь	Ди ит
16,42	0	0,08	-	-
18,53	0,27	0	0,27	-
20,59	0,91	0,15	0,76	0,83
22,35	1,53	0,25	1,28	0,83
24,52	2,58	0,51	2,07	0,80
26,63	3,30	0,65	2,65	0,80
28,50	3,89	1,18	2,70	0,70
30,65	4,71	2,41	2,30	0,49
32,28	5,76	1,93	3,83	0,66
34,53	5,50	2,19	3,31	0,60
36,29	6,50	2,76	3,74	0,57
38,41	6,82	2,73	4,09	0,60
40,41	7,71	4,18	3,53	0,45
42,36	8,41	5,08	3,33	0,39

Анализ результатов экспериментальных исследований, позволяет утверждать, что продольное перемещение частиц вдоль радиусов, выходящих из общего полюса, в процессе осадки в стесненных условиях замедляется, что связано с тесным соприкосновением с неподвижными границами матрицы и является причиной искажения координатной сетки, состоящей первоначально из дуг окружностей при значениях R = const . Из полученных результатов экспериментов следует, что рассматриваемые закономерности невозможно корректно описать с помощью модели «идеальной жидкости».

Решение, в предположении равенства нулю касательных напряжений, для которого предполагалось, что первоначально радиальные линии координатной сетки остаются дугами окружностей в процессе течения не согласуется с экспериментальными данными. Полученные экспериментальные результаты с искривлением координатной сетки вблизи неподвижных границ, более коррек-

тно можно описать с помощью модели «вязкой жидкости».

Выводы. Течение металла образцов при переходе в пластическое состояние происходит ожидаемо – по прямым линиям тока, в данном случае по радиусам, выходящим из общего центра-полюса кругового сектора. Радиальные перемещения вблизи неподвижных стенок отстают от перемещений в центре образца, а максимальные перемещения наблюдаются на линии r = r ₀ при φ=0, которая совпадает с осью симметрии образца. Полученный результат означает, что при течении в тонком пластическом слое возникают ненулевые касательных напряжения и, соответственно, ненулевые скорости угловых деформаций. При сравнении результатов экспериментов с точным решением краевой задачи в рамках математической модели «идеальной жидкости» выявлено, что они находятся в противоречии. Корректное описание течения удается выполнить только в рамках общей математической модели «вязкой жидкости».