К вычислению постоянной времени при решении задачи теплопроводности
Автор: Васильев Юрий Сергеевич, Мустафина Юлия Маулитьяновна
Рубрика: Инженерное оборудование зданий и сооружений
Статья в выпуске: 33 (209), 2010 года.
Бесплатный доступ
Получены приближенные дробно-рациональные формулы для вычисления постоянной времени теплового процесса. Формулы имеют весьма малую погрешность. Рассмотрены канонические формы тел: пластина, цилиндр и шар.
Постоянная времени, дробно-рациональное приближение, алгоритм ремеза
Короткий адрес: https://sciup.org/147154255
IDR: 147154255 | УДК: 621.1.016+517.518.84
Текст научной статьи К вычислению постоянной времени при решении задачи теплопроводности
Ряд инженерных задач связан с изучением процесса теплопроводности. Важной характеристикой такого процесса является постоянная времени. Это величина, с помощью которой можно определить, с какого момента времени процесс можно считать регулярным.
При решении задачи теплопроводности, например, методом Фурье [3], возникает характеристическое уравнение относительно собственного значения и:
F(p,Bi) = 0,
где Bi - безразмерный критерий Био. Вид уравнения зависит от формы тела. Далее под ц будем подразумевать наименьший положительный корень уравнения (1). Постоянная времени Т может быть вычислена следующим образом:
/2
Т = — а
Ц
где / - характерный размер тела; а - коэффициент температуропроводности.
Уравнение (1) может быть трансцендентным и довольно сложным для решения. Представляется полезным получить простые формулы для вычисления ц. В работе [5] были получены такие формулы для бесконечной пластины, когда критерий Био может быть любым из промежутка 0 < Bi < со .
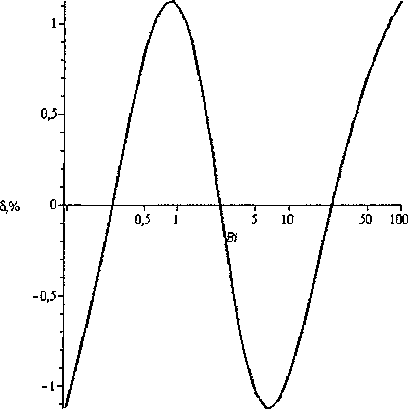
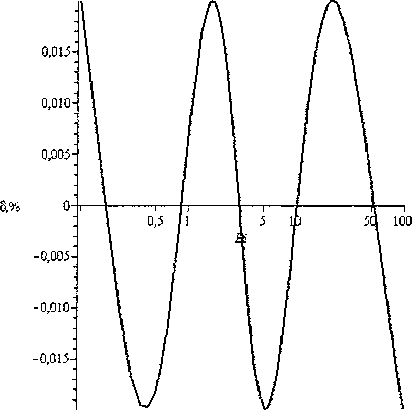
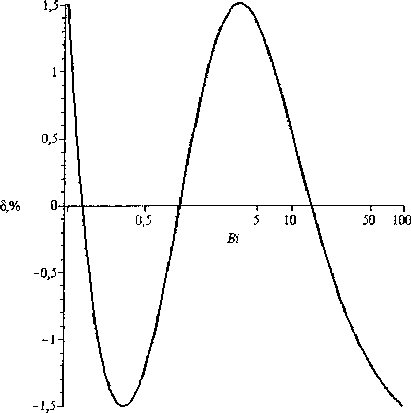
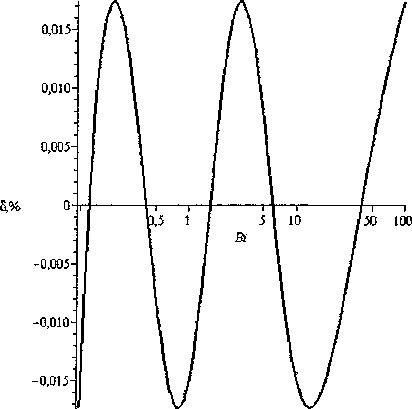
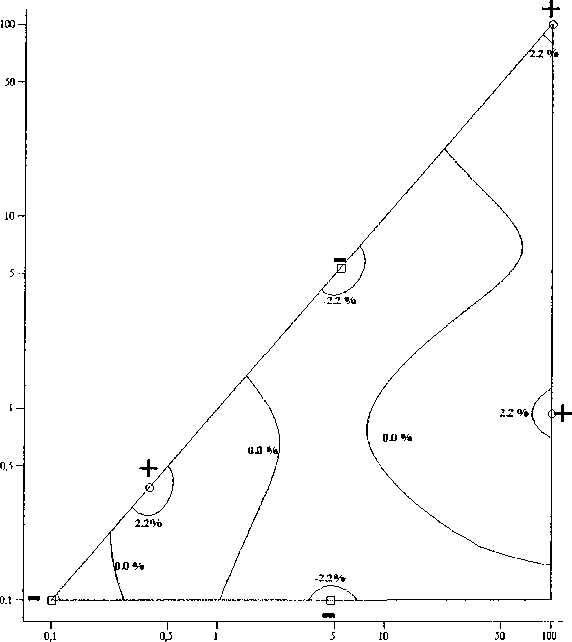
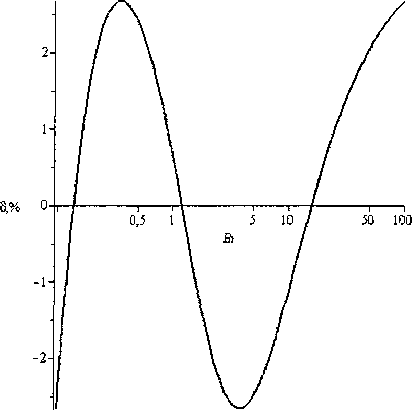
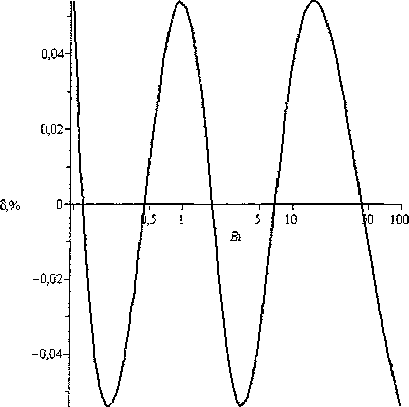
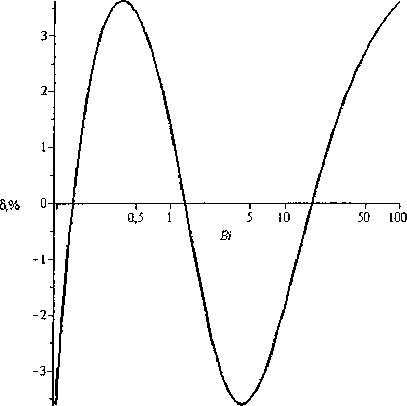
В практических задачах критерий Био находится в промежутке 0,l В данной статье выводятся формулы для приближенного вычисления постоянной времени при выполнении условия 0,1 < Bi < 100. Пластина Процесс теплообмена бесконечной пластины толщины I с окружающей средой описывается уравнением 8t - д2/ л 1 - а—у,0 <х <1, (К) дт где t = tlx, т) - температура; I - толщина пласти ны; т - время. При этом должно выполняться начальное условие /(х,0) = <р(х) и одно из краевых условий на поверхности пластины при х = I, т > 0 : tQ, т) = /н - первого рода, л—(/,т) = ^н -второгорода, Эх (3-1) (3.2) -а(?(7,т)-/н) - третьего рода. (3.3) Здесь а - коэффициент теплоотдачи; X - коэффициент теплопроводности материала пластины; /н - температура наружной среды; дн - плотность теплового потока. Критерий Био Bi = а/ / X . Аналогичные условия ставятся и при х = 0. Краевые условия 1-го и 3-го рода Характеристическое уравнение (1) для сочетания краевых условий вида (3.1) и (3.3) на поверхностях имеет вид pctg(p) = -Bi [1, 3]. Будем считать наименьший положительный корень этого уравнения функцией критерия Био: ц = p(Bi). Введем функцию ц2 (Bi) = 1 / ц2 (Bi). Ее график похож на график дробно-рациональной функции, поэтому будем искать приближение для ц2 (Bi) в виде функции иA-Bi + B М (В1) =--------, (4) v 7 Bi + C где Л, В, С - неизвестные параметры. Относительная погрешность приближения, в процентах, рассчитывается по формуле § (Bi) = ^2 (B1)-^(Bl) . j 00 (5) V (Bi) Подберем коэффициенты А, В, С в выражении (4) так, чтобы достигался минимум максимума относительной погрешности (5) на промежутке 0,1< Bi <100. Для этого воспользуемся алгоритмом Ремеза [2]. При попытке напрямую применить его на этом промежутке, возникают трудности со сходимостью алгоритма. Поэтому сделаем замену переменных Bi = y/(l-y). Тогда если 0,1 < Bi < 100, то переменная у будет принимать значения 0,0909 < у< 0,99. Подставим выражение для Bi в приближение (4), выполним простейшие преобразования, чтобы получить дробно-рациональное выражение относительно у . В результате новое выражение для М^у^ будет иметь вид: А-В 1-С _ А — В _ В С Обозначим D =----, Е =----, F =----. Выра- 1-С 1-С 1-С ... \ Dy + E жение (4) запишется как Mly) =------. y + F Найдем приближение на отрезке 0,0909 < у< 0,9900 с помощью встроенной в пакет Maple функции minimax, вернемся к парамет-F рам А, В, С , используя формулы С =----, 1 + F В = E(l-C^, А = B + D(l-C). В результате получим формулу 0,099^^3347 v ’ Bi+ 0,8079 при этом максимальная погрешность составляет 1,2 % что видно из графика на рис. 1. Это приближение точнее, чем приближение с 5 %-ной погрешностью, полученное в [5]. Для увеличения точности, повысим степени числителя и знаменателя на единицу и будем приближать функцию ц2 (Bi) выражением X-Bi2+BBi + C М (В1) =-------------- Bi2+£>-Bi + £ Найдя коэффициенты с помощью алгоритма Ремеза, полученную формулу запишем в виде A/(Bi) = 0,1014- 0,1681 Bi+ 3,3962 0,3663 Bi+ 1,0374 с целью уменьшить количество арифметических действий. Погрешность этой формулы составляет 0,02 %, что в 60 раз меньше погрешности приближения (7). График погрешности представлен на рис. 2. Краевые условия 2-го и 3-го рода Характеристическое уравнение (1) для сочетания краевых условий вида (3.2) и (3.3) имеет вид Рис. 1. Относительная погрешность формулы (7) Рис. 2. Относительная погрешность формулы (9) ctg(p) = p/Bi [1, 3]. Как и в предыдущем случае, наименьший положительный корень этого уравнения - функция критерия Био: p = p(Bi). Введем функцию p2 (Bi) = 1/ц2 (Bi). Будем искать приближение р2 (Bi) в виде (4). Аналогично предыдущему случаю воспользуемся алгоритмом Ремеза. В результате получим формулу Наименьший положительный корень этого уравнения p = p(s,/?). Введем функцию ц2 (s, р) = 1/ц2 (s, р) ■ Область определения G для , 2,5136Bi — 0,0158 М (Bi) =----------------- v 7 Bi + 2,3718 (Ю) функции р2(5,р) - треугольник АВС, в котором сторона АВ есть парабола р^ = s" ,4, где 0,2 < s < 200 ; стороны ВС и СА - прямолинейные отрезки с уравнениями р (s) = 0, Is - 0,01, 0,2 При этом максимальная погрешность составляет 1,51 %, что видно из графика на рис. 3. Рассмотрим следующее приближение вида (8). После применения алгоритма Ремеза получим, что погрешность составляет 0,018 %, что в 83 раза меньше, чем для приближения (10). Таким образом, формула M(Bi) = 2,4665- 15,4083+ 4,8842 Bi (п) Bi2+4,5079 Bi+ 6,2473 Будем искать приближение p2(s,/?) в виде дробно-рациональной функции M^s,p^ = 1 + As + Bp С + Ds + Ер точнее, чем аналогичная формула на бесконечном промежутке Bi [5] в 44 раза. График погрешности представлен на рис. 4. Краевые условия 3-го рода на обеих границах Для сочетания краевых условий вида (3.3) на обеих поверхностях пластины характеристическое уравнение (1) имеет вид: Относительная погрешность приближения рассчитывается по формуле, аналогичной (5). Перейдем к задаче приближения функции двух переменных рациональной функцией. Нахождение коэффициентов в формуле (14) представляет собой более трудную задачу, чем в одномерном случае. Разработанные алгоритмы имеют ограниченную область применения. Однако, доста точным условием того, что представленное рацио ctg(p) = ц2 — Bi]Bi2 p(Bi,+Bi2) ' Здесь Bi,, Bi2 - критерии Био для поверхностей пластины. Ввиду симметричности этого уравнения относительно Bi,, Bi2, обозначим р = Bi, • Bi2, s = Bi, + Bi2. В новых обозначениях уравнение (12) запишется как 2 _ ctg(p) = ----"• (13) ps нальное выражение наилучшее, является наличие и +1 -точечного ( и - число неизвестных параметров) чебышевского альтернанса, в данном случае шеститочечного. Затруднительным является нахождение первоначального приближения, с которого можно было бы начать поиск минимума нормы функции ошибок. Прямое применение алгоритма Ремеза не дает нужного результата. Поэтому поступим следующим образом. В области G проведем среднюю линию (рис. 5): 0,05s-0,005+ — , s < 100,1; 50s-5000 + — , s > 100,1. Рис. 3. Относительная погрешность формулы (10) Рис. 4. Относительная погрешность формулы (11) Рис. 5. Область определения ц2($’Р) со средней линией Рассмотрим функцию p2(s,p) на средней линии р^. Приближаемая функция тогда есть функция одного переменного /(s) = р2 (^^С5)) ■ Приблизим ее по алгоритму Ремеза дробнорациональным выражением , . / , l + v4s + 5p(s) y(s) = M(s,p(s^=-------. V 7 V c + Ds + Ep^ Получим, что , 1 + 0,4264s+0,1396» v 7 -0,0056 + 1,0220s + l,3926p Будем считать эту дробь начальным приближением к функции ц2 (^, Р^в области G. Уточним полученные коэффициенты методом Нелдера-Мида [4], минимизируя функцию коэффициентов Д В, C,D,E'. g^A,B,C,D,E^ = max v^fVM^iEl v-As’P^ ■ (16) Пользуемся этим методом, потому что он приспособлен для минимизации недифференцируемых функций, какой и является функция g^A,B,C,D,E^. После применения этой процедуры становится ясно, что все точки предполагаемого чебышевского альтернанса расположены на границе области G. Теперь применим алгоритм Ремеза уже на этой границе для дальнейшего уточнения коэффициентов в выражении (14). В итоге получили приближение: х l + 0,4391s + 0,1319p М ( s, р ) =----------------------------. (17) v 7 -0,0179 + 1,0692s + 1,3458р Погрешность приближения (17) составляет 2,4 %. Погрешность аналогичной формулы в [5] составляет 5 %. Для лучшего представления характера погрешности 8(s,p) изобразим ее линии уровня и точки альтернанса в терминах BibBi2 на рис. 6. Рис. 6. Линии уровня и точки альтернанса функции ошибок 8(Bit,Bi2) Наличие именно шести точек альтернанса, обозначенных на рис. 6 знаками «+» и «-», говорит о том, что полученное приближение наилучшее. Цилиндр Процесс теплообмена бесконечного цилиндра радиуса г0 с окружающей средой описывается уравнением: " + ’ °-г-г0’ (18) от г or j где ^ = /(г,т) - температура, г - расстояние до оси цилиндра. При этом должно выполняться начальное условие l(r,O) = F^ и одно из краевых условий первого, второго или третьего рода на поверхности цилиндра. Краевое условие 1-го или 2-го рода Краевым условиям 1-го или 2-го рода, аналогичным (3.1) и (3.2), соответствуют характеристические уравнения (1) Jo(p) = O и .^(ц^О соответственно [3]. Здесь J0(p), ^(ц) - функции Бесселя первого рода. Так как первые корни есть 2,405 и 3,832, то из формулы (2) получим, что соответствующие постоянные времени 2 2 Д =0,1729-^- и Д, = 0,0681—. а а Краевое условие 3-го рода Рассмотрим условие 3-го рода вида (3.3). Характеристическое уравнение имеет вид =—, где В1 = аг0/Л [3]. Найдем прибли- Л(р) Bi жения функции ц2 (Bi) = 1/ц2 (Bi) аналогично случаю краевых условий 1-го и 3-го рода для пластины. Относительная погрешность выражается формулой (5). Воспользуемся алгоритмом Ремеза, в результате получим: A/(Bi) = 0,1671 Bi+ 0,4567 Bi —0,0101 При этом максимальная погрешность состав ляет 2,7 % что видно из графика на рис. 7. Проведем аппроксимацию дробно-рациональным выражением (8). В результате работы алгоритма Ремеза получим формулу: M(Bi) = 0,1731- 0,1687 Bi + 3,0518 0,5025 4--~ . Bi+ 4,2720-КГ4 Ее погрешность составляет 0,054 %, что в 50 раз меньше погрешности предыдущего приближения (19). График погрешности представлен на рис. 8. Шар Процесс теплообмена шара радиуса г0 с ок ружающей средой описывается уравнением: где 1 = /(г,т) - температура, г - расстояние до центра шара. Выполняется начальное условие ?(r,0) = F^ и одно из краевых условий первого, второго или третьего рода на поверхности шара. Краевое условие 1-го или 2-го рода Для краевого условия на поверхности шара 1-го рода, аналогичного (3.1), или 2-го рода, аналогичного (3.2), характеристические уравнения (1) имеют вид sinp = O и tgp = p [3]. Так как корни этих уравнений известны, то из формулы (2) получим, что постоянные времени для этих случаев 1 г2 г2 Д И Тй = 0,0495—. л2а а Краевое условие 3-го рода Рассмотрим условие 3-го рода вида (3.3). Для Рис. 7. Относительная погрешность формулы (19) Рис. 8. Относительная погрешность формулы (20) Формулы постоянной времени для неограниченной пластины уравнение — = а—4г, 0 < х < I; Bi = —, Bi е [0,1; 100] Зт X Таблица 1 Краевые условия Характеристическое уравнение Формулы для постоянной времени Т Приближение 1-й степени, (погрешность) Приближение 2-й степени, (погрешность) I и III рода 1(0,т) = 1„, pctg(p) = -Bi /20,0997Bi +0,3347 a Bi+ 0,8079 ° —Г 0,1014--0Д681_ + _О3663_^ Bi + 3,3962 Bi + l,0374j II и III рода сМи)^1.- 2,5136Bi-0,0158 1 a Bi + 2,3718 " У 2,4665- ^083 + 4,884281) (0 0]g %) Bi2 + 4,507961 + 6,2473 J III и III рода Х^1’^ = "а1К1’хУ^ ctgw=^ V ' p(Bi1+Bi2) /2 l + 0,4391(Bi, + Bi2) + 0,1319Bi.Bi2 ----’------------1-^---, (2,4%) а -0,0179 + 1,0692(81] +Bi2) + l,3458Bi,Bi2 Формулы постоянной времени для бесконечного цилиндра Вестник ЮУрГУ, № 33, 2010 Таблица 2 уравнение — = + 0 < г < r0; Bi = ^-, Bi е [0,1;100] Зт I dr2г 8r I X Краевое условие Характеристическое уравнение Формулы для постоянной времени Т Приближение 1-й степени, (погрешность 2,7 %) Приближение 2-й степени, (погрешность 0,054 %) III рода х^(го>т) = ~«('('о.т)-<и) 2, (ц) Bi г02 0,167 lBi +0,4567 a Bi-0,0101 i.4 о 1731 - °’1687 + °’5025 1 ’ Bi + 3,0518 Bi+ 4,2720-10-4 J Формулы постоянной времени для шара Таблица 3 уравнение — = ~- + —0 < г< r0; Bi = ^-, Bi е [0,1; 100] Зт I dr г 8r I X Краевое условие Характеристическое уравнение Формулы для постоянной времени Т Приближение 1-й степени, (погрешность 3,6 %) Приближение 2-й степени, (погрешность 0,1 %) III рода tgp = —Н— Bi-1 г02 0,0966Bi +0,2983 a Bi-0,0125 5Lfo 1015 0)3359 | 0)1480 ) Bi + 6,8514-Ю"4 Bi + 3,5761J Инженерное оборудование зданий и сооружений Рис. 9. Относительная погрешность формулы (22) Рис. 10. Относительная погрешность формулы (23) него характеристическое уравнение: tg ц = - Bi —1 где Bi = apJX [3]. Приблизим функцию р2 (Bi) = 1 / р2 (Bi) дробно-рациональными выра жениями вида (4) и (8). Как и в предыдущей задаче, воспользуемся алгоритмом Ремеза. В результате получим формулу M(Bi) = 0,0966 Bi+ 0,2983 Bi-0,0125 При этом максимальная погрешность (5) составляет 3,6 %, что видно из графика на рис. 9. Для получения приближения с меньшей погрешностью воспользуемся выражением (8). После применения алгоритма Ремеза (с промежуточной заменой переменных), получим формулу: АГ (Bi) = 0,1015- 0,3359 Bi + 6,8514-104 0,1480 Bi + 3,5761 ’ погрешность (5) которой составляет уже 0,1 %, что в 36 раз меньше погрешности предыдущего приближения (22). График погрешности представлен на рис. 10. Сводка результатов Сведем все полученные формулы в табл. 1-3. В табл. 1 приведены приближенные формулы с погрешностями существенно меньшими, чем полученные в работе [5]. Заключение Для постоянной времени теплового процесса выведены простые дробно-рациональные формулы с наименьшей относительной погрешностью, позволяющие не решать трансцендентного уравнения. Формулы удобны в практических расчетах, а также при программировании устройств управления, использующих значение постоянной времени в процессе работы.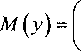
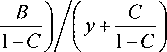
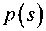
Список литературы К вычислению постоянной времени при решении задачи теплопроводности
- Лыков А.В. Теория теплопроводности/А.В. Лыков. -М.: Высшая школа, 1967. -599 с.
- Ремез Е.Я. Основы численных методов чебышевского приближения/Е.Я. Ремез. -Киев: Наукова думка, 1969. -624 с.
- Теплопередача/В.П. Исаченко, В.А. Осипова, А.С. Сукомел. -М.: Энергоиздат, 1981. -416 с.
- Численные методы. Использование MATLAB/Джон Г. Мэтьюз, Куртис Д. Финк. -М.: Издательский дом «Вильямс», 2001. -720 с.
- Васильев Ю.С. Инженерные формулы для определения постоянной времени/Ю.С. Васильев, А.В. Донская//Вестник ЮУрГУ. Серия «Строительство и архитектура». -2009. -Вып. 8. -№16.-С. 43-48.


