К выводу уравнений регулирования и анализу особенностей гидравлических режимов открытых систем теплоснабжения без регуляторов расхода на абонентских вводах

Введение. Известно, что открытые системы теплоснабжения на базе теплоэлектроцентралей (ТЭЦ) отличаются высокой энергетической эффективностью «...прежде всего потому, что позволяют максимально реализовать эффект комбинированной выработки электрической и тепловой энергии за счёт использования низкопотенциальных источников теплоты для подогрева больших количеств подпиточной воды теплосети на ТЭЦ» [1]. В [1] также указывается, что «…применение открытых систем полностью соответствует положениям федеральных законов об энергосбережении и о теплоснабжении», что существовавшие преимущества закрытых систем перед открытыми «…в современных условиях стали минимальными», что «...выработка электроэнергии на тепловом потреблении, определяющая энергетическую эффективность ТЭЦ, на станциях, к которым подключены закрытые системы теплоснабжения, всегда гораздо ниже, чем на ТЭЦ с открытыми системами».

Вместе с тем объективности ради следует также отметить, что закрытые системы по сравнению с открытыми характеризуются рядом своих преимуществ, которые могут быть и востребованы в определенных условиях, поэтому, учитывая 48

в том числе и данные работ [1–5], можно заключить, что как закрытые, так и открытые системы теплоснабжения имеют полное право на существование, что проблема выбора типа системы теплоснабжения должна решаться «…прежде всего, исходя из энергетической эффективности теплофикационных систем и с учётом качества исходной воды в источниках водоснабжения конкретных городов» [1]. Укажем также дополнительно, что к настоящему времени запрет на использование существующих открытых систем теплоснабжения отменен [6], что и обуславливает актуальность рассмотрения вопросов, связанных с их эксплуатацией и эффективностью функционирования [7, 8].

Постановка задачи. Как это хорошо известно, «…объективным недостатком открытых систем … является сложный гидравлический режим из-за переменного расхода воды на ГВС» (примечание: ГВС – горячее водоснабжение) [1], что «…нестабильность гидравлического режима является очень значимым отрицательным эксплуатационным фактором» [4]. Поэтому рассмотрим вопросы, связанные с выводом и детальной «расшифровкой» некоторых соотношений для гидравлических режимов открытых систем теплоснабже- ния без регуляторов расхода на абонентских вво- зом [12]: 1) полные напоры перед элеваторами дах. Эти соотношения могут быть использованы всех абонентских вводов при выключенном водо-как для наполнения алгоритмического обеспече- разборе должны быть одинаковыми; 2) полные ния автоматизированных систем управления теп- напоры после систем отопления также при выклю-лоснабжением - при использовании таких систем ченном водоразборе должны быть одинаковыми у проблемы поддержания требуемого гидравличе- всех абонентов; 3) водоразбор на ГВС из подаю-ского режима практически устраняются, так и в щих линий абонентских вводов должен осуществ-учебных целях - в известных литературных источ- ляться перед элеваторами, а из обратных - после никах [9–12] как детали вывода, так и их обосно- отопительных установок; 4) у всех абонентов от-ванность, по существу, не приводятся и не разъяс- ношение расчетных расходов воды на ГВС и ото-няются в должной мере. Кроме того, их анализ не пление должно быть приблизительно одинаково.

является достаточно подробным. К месту также Условия 1 и 2 (это так называемый принцип заметим, что, как это нам представляется, данные «горизонтальной дорожки С.А. Чистовича» [12]) соотношения были предложены в свое время обеспечиваются подбором диафрагм, устанавли-С.А. Чистовичем [9-12]. ваемых на подающих и обратных линиях абонент-

Используемые допущения. Для управляемо- ских вводов (рис.1). В целом вышеотмеченное ил-сти сеть должна быть настроена следующим обра- люстрируется рис. 1.

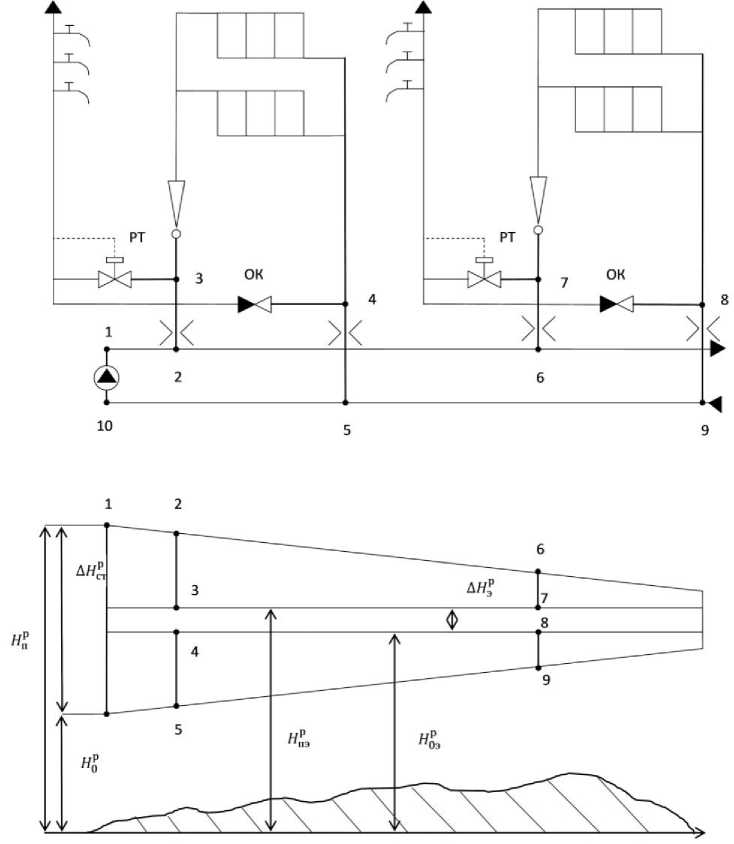
Рис. 1. Схема системы теплоснабжения и пьезометрический график при отсутствии водоразбора: 1–2 – пьезометрический график участка 1–2 подающей магистрали теплосети; 2–3 – пьезометрический график участка 2–3 подающей линии 1-го абонентского ввода; (требуемое падение напора обеспечивается подбором диафрагмы); 4–5 – пьезометрический график участка 4–5 обратной линии 1-го абонентского ввода; 5–10 пьезометрический график участка 5–10 обратной магистрали участка теплосети. Для 2-го абонента используются аналогичные обозначения графиков и участков нП и НО - полные напоры в подающем и обратном коллекторах источника теплоснабжения; АНСТ - разность напоров между подающим и обратным коллекторами; нПэ - полный напор перед элеваторами абонентских вводов; АНЭ -падение напора в системах отопления (СО) – элеваторах; нОЭ - полный напор после элеваторов -СО. Верхний индекс «р» используется для обозначения расчетного режима (при отсутствии водо-разбора). ОК – обратный клапан, РТ – регулятор температуры воды в системе горячего водоснабжения.

В целом используемые на рис. 1 обозначения являются общепринятыми.

Решение задачи. При выполнении этих условий данную теплосеть можно заменить эквивалентной сетью с одним эквивалентным абонентом, расход воды у которого равен сумме расходов всех абонентов (рис. 2).

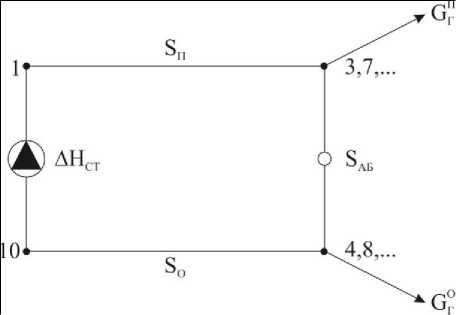
Рис. 2. Схема эквивалентной тепловой сети

Считается, что в сети имеет место квадратичный гидравлический режим, кроме того, справедливы и законы Кирхгофа для гидравлических цепей [13–15].

Параметры расчетного режима позволяют определить гидравлические сопротивления эквивалентного абонента SАБ и подающей Sn и обратной

S o магистралей эквивалентной тепловой сети:

₌ (Н П - Н Пэ ) -p g (G o ) 2       ^;

₌ АН Р -p g

¹ (G O ) 2   ^;

_ ^(Н Оэ - ^Н О ) ^{-p g}

(G O )²

Здесь GO - расчетный расход воды на отопление всех реальных абонентов. Кроме того, для общего сопротивления сети можно записать сле- дующие   соотношения:    S = Sn + Sae + SO ^

1 = S_n/S + S_АБ/S + S_O/S

Введем также и следующие обозначения:

^{G        G}r ..  ^G                     П

Y = — ; P = — ; Ф = — - здесь и далее G_г , G O      ^G r      G O

Go и Gr соответственно расход воды на ГВС из подающей и обратной магистралей и общий расход воды на ГВС.

Выразим G П , G^O , а также и потерю напора на эквивалентном абоненте через G O :

G ? =p G r =PyG O ;                    (4)

G O = G r - G ? = yG O - PyG O = Y (1 - P )G O ; (5)

АН аб = S АБ G O = S ae ^O) 2 = S^ 2 (G O ) 2 . (6)

Расход воды по подающей линии эквивалентной сети в нерасчетном режиме согласно 1-му закону Кирхгофа будет равен

G o+G? = фGO +PyGO = (9 + pY)GO,(7)

в соответствии с этим потеря напора на этом участке будет следующей:

АНП = Sn (Ф + PY)2(GO )2 .(8)

Расход воды по обратной линии эквивалентной сети в нерасчетном режиме будет таков:

G о - G O = ф G O -Y (1 -P )G O =

= [9-Y(1-P)]GO.(9)

Поэтому потеря напора на обратной линии будет определяться следующим выражением:

АНо = Sо[ф-Y(1-P)]2(GO)2 .(10)

Таким образом, для всей эквивалентной тепловой сети можно записать

АН ст = АН п + АН аб + А Н о = {( Ф + Py)² S п +

+Ф2SАБ + [ф-Y(1-P)]2Sо}(G0)2 .(11)

Через АНСТ = S(GO)2 данное соотношение можно переписать так:

АН с _Т =АН Ст {(ф + Py)² S ? /S + ф ²S АБ /S +

+[Ф-Y(1 -P)]2So/S}.(12)

Данное уравнение показывает, как следует изменять разность напоров на ТЭЦ в зависимости от величины водоразбора – коэффициент γ , от режима отопления – коэффициент φ и температуры наружного воздуха – коэффициент β .

Как это нетрудно показать, коэффициент β является функцией температуры воды в подающей и обратной магистралях или, что то же самое при качественном регулировании, – температуры наружного воздуха.

В самом деле, теплота, содержащаяся в общем расходе воды на ГВС, должна равняться теплоте в расходе воды на ГВС из подающей линии и теплоте в расходе воды на ГВС из обратной линии:

cG_rt_r = еО П t_n + cG O t_o.                (13)

Поэтому

G O = G_r - G n ^ G_r t Г = G n t_n + (G_r - G n )t_o ^

^ t_r =p t n + (1 -P )t o ^ P = t t .

t П   t o

Здесь t Г = const - температура воды в системе ГВС, а температуры теплоносителя в подающей t п и обратной t_o магистралях являются функциями температуры наружного воздуха.

Если поставлена задача – обеспечить расчетный режим отопления (это когда ф = 1), то алгоритм управления напорами на ТЭЦ в зависимости от режима водоразбора и температуры наружного воздуха таков

АИ ст = аи Ст {(1 + ру ) 2 S n / S + S АБ / S +

+ [1 -Y (1 -P )]²S o /S}.                      (14)

Если при этом водоразбора нет (коэффициент у = 0), то АИ_Ст =A H C _T{S_n/S + S_АБ/S + S_o/S} = = А И СТ - что так и должно быть.

При водоразборе только из подающей линии (температура наружного воздуха такая!) и при расчетном режиме отопления ( р = 1 и ф = 1) в зависимости от величины водоразбора у должно быть

АИ_Ст = А И СТ {(1 + у )² S_n / S + S_АБ / S + S_o / S} =

= ^АБ /S + S o /S = 1 - S n /S| =

= АИ Ст {1 + у (2 + y )S n /S}.                (15)

Из данной формулы следует, что с увеличением величины водоразбора у для обеспечения расчетного режима отопления необходимо повышать разность напоров между подающим и обратным коллекторами ТЭЦ. Это и вполне понятно: с увеличением у растет расход воды по подающей магистрали, следовательно, растет и потеря напора на этой линии, потеря напора на абонентском вводе и обратной линии при этом будет одной и той же, так как по этим элементам расход воды всегда равен G o . Поэтому для компенсации растущей потери напора в сети необходимо увеличивать ^{А И}ст .

При водоразборе только из обратной линии и при расчетном режиме отопления ( р = 0 и ф = 1) в зависимости от величины водоразбора у должно быть

АИ ст = АИ Ст {S n / S + S ab / S + [1 - у ]² S o / S} =

= |S n /S + S АБ /S = 1 - S o /S| =

= АИ Ст {1 + y(y- 2)S o /S}.               (16)

Коэффициент y по физическому смыслу может изменяться только в пределах от нуля до еди- ницы, поэтому фигурная скобка в (16) при увеличении у от нуля до единицы будет уменьшаться от 1 до 1 - So / S, следовательно, с увеличением водоразбора для обеспечения расчетного расхода воды на отопление АИст необходимо уменьшать. Это также вполне понятно: так как по подающей линии и через абонентский ввод расход один и тот же и равен Go, то и потеря напора на этих элементах всегда одна и та же, потеря напора на обратной магистрали будет уменьшаться из-за того, что вода на ГВС забирается из этой линии и расход воды по ней будет падать.

Из уравнения (12) следует:

A И_ст/ A И Р_Т = ф ² S_п/S+2 PYф S_п/S+

+р ² у ² S_n / S+ ф ² S_AE / S+ ф ² S_o / S-

-2 фу (1- P )S o /S+ у ² (1- Р )² S o /S.        (17)

Или же

АИ_ст / А И^р_т =

= ф ² + 2 ф [ PY S n /S -у (1 -p )S o /S] +

+p ² y ²S n /S + y ²(1 -p )²S o /S.              (18)

Выделим полный квадрат по ф , введя предварительно обозначение [PySn / S - у(1 - P)So / SJ = [•], в результате получим ф2 + 2фИ + И2 -[-J2 +P2yX /S +

+у ²(1 -P )²S_o/S -АИ_Ст / А И СТ = 0 .      (19)

Или же

{ ф+м: ' =А И ст / аи Ст + н² -

- p ² y ²S n /S -у ²(1 -р )²S o /S.             (20)

Поскольку нам интересен только неотрицательный корень этого уравнения, то будем иметь ф = -И +

+ 7а И _Ст / аи Ст + [ • J² - e ² Y ²S_n / S - у ² (1 - в )² S_o / S . ⁽²¹)

Исследование полученного решения. Рассмотрим, какое влияние водоразбор на нужды ГВС оказывает на гидравлический режим отопительных установок при постоянном напоре на коллекторах источника теплоснабжения.

При водоразборе только из подающей линии (р = 1) и при постоянном напоре на коллекторах источника (АИсТ / АИСТ = 1) формула (21) прини- мает вид

Sn и 2 ф = -у • —^П + , 1 + у •

Графики данной зависимости для различных значений величины водоразбора (коэффициент у )

и различных значений относительного сопротивления подающей магистрали Sn / S приведены на рис. 3.

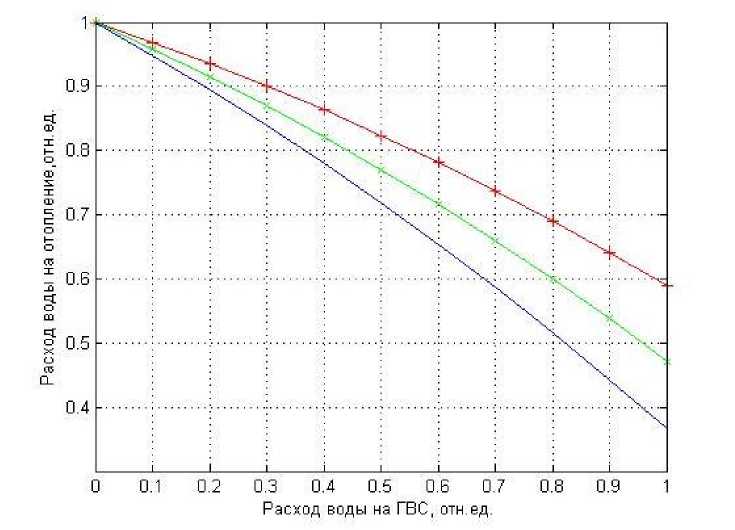
Рис. 3. Кривые зависимости ф от у при р = 1

Здесь для верхней кривой S_n /S = 0,3, для средней S_n /S = 0,4 и для нижней кривой S_n/S = 0,5.

Как видно из рис. 3, при А И СТ / А И СТ = 1 увеличение водоразбора из подающей линии приводит к уменьшению расхода воды на отопление, причем тем значительнее, чем больше относительное сопротивление подающей магистрали.

Это и вполне понятно, так как

источника ( А И СТ / А И СТ = 1) относительный рас-

ход воды на отопление будет вычисляться по следующей формуле:

So „   2

ф = у.“О + « 1 + Y •

S o S

।2        S

— Y2 • —

S

.

Данная зависимость иллюстрируется рис. 4.

Здесь для верхней кривой S_o /S = 0,5, для

дф S              । S 1

— = —П + y[1 + y • П dy     S           ( S J

—

- у ² .1 S n 1 ] 2 . S n (S n — i) <  о .

I S J      S S

Однако при этом общий расход по подающей линии (О О + О Г ) = ( ф+у )О О растет, так как

средней So / S = 0,4 и для нижней кривой So / S = 0,3 .

Как видно из рис. 4, увеличение водоразбора из обратной линии приводит к увеличению расхода воды на отопление (наблюдается так называемый «перетоп»). При этом чем больше относительное сопротивление обратной магистрали, тем значительнее «перетоп». Объясняется это тем, что в данном случае

= So +Y[1 + Y2 .f So 1 — dY S           ( S J

^О ^{+ О} Г ) = { Y (1 — —) + Y [1 + y 2 .f S T 1 dY              S            ( S J

— y ² { s ) ² • s Ф—^o > ⁰ ;

—

— Y ² .1 S o | ] 2 • S o (S o — 1) > 0 .

I S J       S S

S

При — = 0,5

5 (О о + О_r)_ 5 ( ф + Y )О О

d2-0 5     0,25y

, 5       ;------------------ , dY        V1 — 0,25y2

если

dY

dY

= ( ^дф + 1)О О >  0 . (24) dY

учесть, что 0 1, то 0,2113 < — <  0,5 . dY

дф

дФ     дф

Здесь нужно учитывать, что — < 1 и — < 0 .

dY       dY

dY

So

При — = 0,3

^ = 0,3 — ^dY

0,21y

При водоразборе только из обратной линии ( P = 0) и при постоянном напоре на коллекторах

,

V1 — 0,21y ²

если

учесть, что 0 <  y <  1, то 0,0637 < — <  0,3 . dy

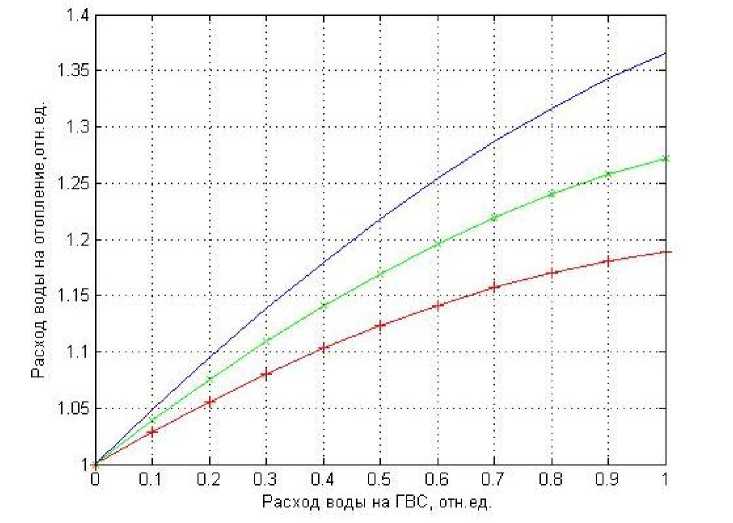
Рис. 4. Кривые зависимости ϕ от γ при β= 0

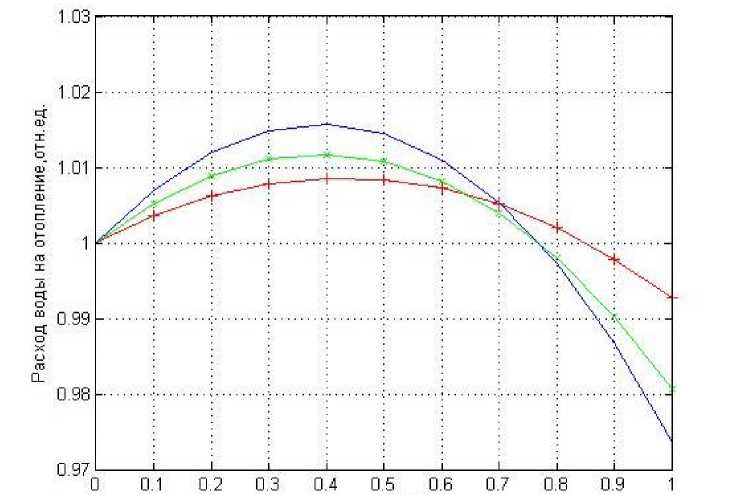
Далее выясним, какой вид имеет график уравнения (21) при β=0, 4 , ΔHСТ = ΔHСРТ = const для следующих диапазонов изменения относительных сопротивлений подающей и обратной магистралей 0≤SП/S≤0,5 и 0≤SО/S≤0,5 . В [12] утвержда- ется, что в этом случае ϕ≈1 , т. е. расход воды на отопление примерно равен расчетному значению, однако при этом никаких конкретных данных не приводится.

На рис. 5 для кривой, отмеченной знаком «плюс», S_П/S = S_О/S = 0,2 , для кривой, отмечен-

Расход воды на ГВС, отн.ед

Рис. 5. График уравнения (21) при β= 0,4 при одинаковых сопротивлениях магистралей

при неодинаковых сопротивлениях магистралей

ной крестиками, S_П /S = S o /S = 0,3 и для 3-й кривой S_П / S = S_o / S = 0,4.

Как видно из рис. 5, погрешность поддержания расчетного расхода воды на отопление в рассмотренном случае не превышает 3 %, что вполне удовлетворительно. Однако при этом следует заметить, что в = 0,4 лишь при определенной температуре наружного воздуха. Здесь также следует отметить, что чем больше относительное сопротивление магистралей, тем больше и погрешность.

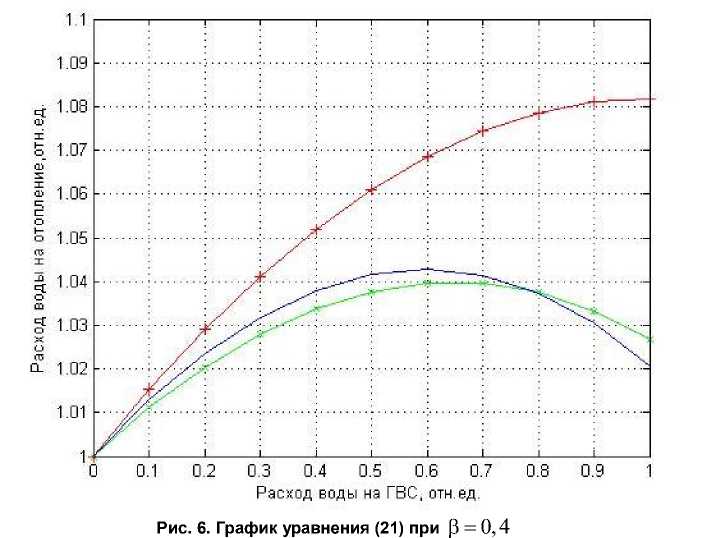
На рис. 6 для кривой, отмеченной знаком «плюс», S_П / S = 0,2;S_o / S = 0,4, для кривой, отмеченной крестиками, S п /S = 0,3;S o /S = 0,4 и для 3-й кривой S_П /S = 0,4; S_o /S = 0,5.

Как видно из рис. 6, погрешность поддержания расчетного расхода воды на отопление уже может достигать почти 9 %, причем эта погреш- ность тем больше, чем больше разность между сопротивлениями магистралей сети.

Выводы

Рассмотрен вывод соотношений для гидравлического режима открытых тепловых сетей, настроенных по принципу «горизонтальной дорожки С.А. Чистовича». Проведен анализ полученных решений для некоторых конкретных случаев, в частности, исследовано влияние величины водо-разбора на режим отопления абонентов при различных характеристиках системы теплоснабжения и температуры наружного воздуха. Полученные уравнения могут быть использованы как для наполнения алгоритмического обеспечения автоматизированных систем управления теплоснабжением, так и в учебных целях – в известных литературных источниках [9–12] как детали вывода, так и их обоснованность, по существу, не приводятся и не разъясняются в должной мере.