К задаче конструирования автоматического регулятора для статического объекта первого порядка с запаздыванием

Введение 1

Широко известно, что наибольшая экономия тепловой энергии в системах теплоснабжения зда-ний достигается за счет их автоматизации, поэто-му разработка вопросов, связанных с проблемой построения высококачественных систем автома-тического управления, является вполне актуальной задачей. В настоящее время в промышленности,В том числе и в системах теплоснабжения зданий для автоматического регулирования различных переменных технологических процессов, широко используются ПИД-регуляторы и их частные ва-рианты . Накоплен огромнейший опыт применения таких регуляторов, в частности, разработаны и апробированы различные способы их настройки. Вместе с тем, как неоднократно отмечает В .Я. Ро -тач в своем сравнительно недавно изданном учеб-нике [1], п-, пи- и ПИД- «…алгоритмы были по-лучены чисто эвристическим путем» [1, с . 82 И др.] и что «…достаточно убедительное формальное

… до сих пор получить не удалось» [1, с. 24].

В работе [2], как нам представляется, удалось получить некоторое формальное обоснование це-лесообразности применения ПИД-регуляторов, здесь задача решалась методом «подгонки» пере -даточной функции замкнутой системы автомати-ческого регулирования к некоторому достаточно разумному и практически достижимому виду . Найдены эталонные структуры и настройки регу-ляторов для типовых динамических характеристик промышленных объектов управления, при этом установлено, что все эти регуляторы принадлежат ПИД-семейству. Казалось бы, что поставленная цель достигнута, однако для полноты исследова-ния проблемы необходимо рассмотреть вопрос о качестве переходных процессов (ПП) в таких сис -темах и о грубости этих структур и настроек, дан -ная задача и решается в настоящей работе для од-ного из типовых объектов управления.

Постановка задачи

Рассмотрим вопрос о качестве переходных процессов и о грубости систем автоматического

..          , ..

регулирования (САР) с объектом управления с передаточной функцией вида

W б( Р ^{) =} _т k⁰⁶ . ^ex P⁽-^Tоб Р ),               ⁽¹⁾

^ТобР +¹

где к0б, Тоб, тоб - соответственно коэффициент передачи, постоянная времени и время запаздывания объекта; p - комплексная переменная. В со ответствии с [2] близким к идеальному для такого объекта будет ПИ-регулятор с передаточной функцией

W_P ( Р ) =

T ко б^об+б)

1 н--. Tp

Здесь 9 - постоянная времени эталонной передаточной функции замкнутой системы

W с⁽ P ¹ —Ae^{x|p Т} об Р ).

9 p + 1

Требуется оценить устойчивость САР и качество переходных процессов в ней при вариациях пара -метров настройки регулятора и параметров объек-та управления.

Методика решения задачи

Для анализа переходных процессов в системе с объектом управления данного типа разработаны две компьютерные программы: одна для анализа переходных процессов при возмущении по зада -нию, а другая - при возмущении со стороны регулирующего органа. В каждой из разработанных программ предусмотрен ввод к _0б, Т _об, т_об , а также коэффициента передачи ПИ-регулятора к_р и времени интегрирования Т_и , каждая из программ не только осуществляет построение графика пере -ходного процесса, но и определяет перерегулирование ст и время регулирования t_p , а также вычисляет значения критериев: ^t

1 1 = J|s( t )| dt ;                                      (2)

0 ^t

12 = ^²(t ) dt ,                                 (3)

где t_K - конечное время оценки переходного процесса ; s( t )= x³ ( t )- x ( t ) - ошибка регулирования (рассогласование); x³ ( t ) и x ( t ) - соответственно заданное и действительное значение регулируемой величины; t - время. При этом время регулирования t _p определялось как время, по истечение которого отклонение регулируемой величины от за -дания не будет превышать 5 %.

Интегрирование дифференциального уравне-ния объекта управления осуществлялось методом Рунге -Кутты с погрешностью, пропорциональной пятой степени шага по времени. Для компьютерного использования алгоритм ПИ -регулирования представляли в дискретной форме, при вычислении интеграла применяли метод трапеций. С целью сокращения объема необходимых вычислений использовали рекуррентную форму дискретного представления алгоритма ПИ-регулирования, приведенную в работе [3]:

U ( m )= U ( m- 1) + q _ое( m ) + q 1e( m -1), (4) где m - номер расчетного шага по времени; q о = к_р [1 + hl (2 Т _и)]; q1 =к^1 (2 Т _И )-1]; h - величина шага по времени; U - выходная величина регулятора (% хода исполнительного механизма (ИМ)). В программах предусматривается ввод нижнего и верхнего пределов изменения регули -рующего воздействия U .

Вариация параметров настройки регулятора

Исследование качества переходных процессов в САР проводилось в окрестности базовых настроек:

T

^{; к} о б^об+б)

Т = Т.

и об,

при этом в координатах « к_р • • • Т_и » точка с базовыми настройками располагалась в центре прямо -угольника, вычисления проводились для настроек, расположенных на диагоналях и на отрезках пря-мых, соединяющих середины противоположных сторон прямоугольника (рис. 1).

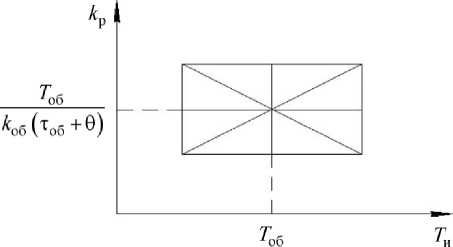
. 1.

настройки регулятора

Сначала параметр 9 полагался равным ну -лю. Пусть, например, к _об =1,5 т/ч/% хода ИМ; Т _об = 15 с; т_об=5 с (параметры объекта управления соответствуют динамическим свойствам кана -ла «расход топлива - тепловая нагрузка» котельной установки [4]). В этом случае базовые значения параметров настройки регулятора равны:

T к = ———=2% хода ИМ/т/ч; Т тТ б =15 c. k

Результаты расчетов показателей качества пере -ходных процессов при возмущении по заданию приведены в табл. 1-3.

Как видно из табл. 1-3, в значимой по размерам окрестности базовой точки

T к = ———=2 % хода ИМ/т/ч; Т тТ^ =15 c k

Таблица 1

Показатели качества переходных процессов при T _{1 =} 15c и различных значениях k при возмущении по заданию

% хода ИМ \ k р , 1      т/ч	1,0	1,5	2,0	2,5	3,0	3,5
ст,%	0	0	0	0,79	9,70	со ( расходя-щийся 1111)
t р,С	53,8	49,9	44,6	55,2	130,8	ОО
I 1,(т/ч )•С	24,81	21,49	19,82	18,98	24,18	ОО
I 2,(т/ч)2 •С	17,34	14,71	13,28	12,46	12,51	ОО

Таблица 2

Показатели качества переходных процессов при k _р =2%хода И М /т/ч и различных значениях T при возмущении по заданию

T ,c	5,0	7,0	10,0	13,0	15,0	17,0	20,0
ст,%	со ( расходя-щийся 1111)	43,38	8,42	0,03	0	0	0
t р,С	ОО	114,1	38,9	40,2	44,6	58,2	68,3
I 1,(т/ч )•С	ОО	25,24	15,04	17,18	19,82	22,44	26,51
I 2,(т/ч)2 •с	ОО	12,47	10,92	12,18	13,28	14,46	16,31

Таблица 3

Показатели качества переходных процессов при различных значениях k р ^иT при возмущении по заданию

k %хода ИМ k р,	1,0	1,0	1,5	1,5	2,5	2,5	3,0	3,0
T ,c	10,0	20,0	12,5	17,5	12,5	17,5	10,0	20,0
ст,%	4,80	0	0	0	5,43	0,01	со ( эасходя-щийся 1111)	1,99
t р ,С	27,2	80,6	41,2	61,4	55,6	56,9	ОО	88,7
I 1,(т/ч ) •С	17,92	33,18	17,91	25,13	17,38	22,02	ОО	24,33
I 2,(т/ч)2 •С	13,86	21,23	13,18	16,34	11,33	13,81	ОО	14,67

САР достаточно устойчивая и качество переход-ных процессов вполне удовлетворительное. Сле -довательно, можно сделать заключение, что рас-сматриваемая система достаточно робастная по отношению к настройкам регулятора при возму-щении по заданию .

Для всех рассмотренных настроек ПИ-регуля-тора определили качество переходных процессов и при возмущении по нагрузке (со стороны регули-рующего органа), результаты вычислений приве-дены в табл. 4‒6.

Как видно из табл. 4‒6, также в значимой по размерам окрестности базовой точки k >б =2% хода ИМ /т/ч;T1 =T )б =15c k

САР достаточно устойчивая и качество переход-ных процессов вполне удовлетворительное и при возмущении по нагрузке . Следовательно , можно сделать заключение, что рассматриваемая система достаточно робастная по отношению к настройкам регулятора и при возмущении со стороны регули-рующего органа.

Сравнивая качество переходных процессов при возмущении по заданию и при возмущении по нагрузке при одинаковых настройках регулятора, можно отметить, что в целом, по нашим оценкам, рассматриваемая САР все- -ет возмущение по заданию, показатели качества переходных процессов принимают более жела-тельные значения . По -видимому, все это является следствием применяемого подхода к решению задачи синтеза САР : -тать возмущение именно по каналу задания.

Настройки ПИ-регулятора, оптимальные по критериям (2) и (3), могут не совпадать как между собой, так и с базовой настройкой, но в целом их различие достаточно небольшое .

Таблица 4

Показатели качества переходных процессов при T _{1 =} 15c и различных значениях k_р при возмущении по нагрузке

% хода ИМ k р , т/ч	1,0	1,5	2,0	2,5	3,0	3,5
ст,%	0	0	0,19	19,33	40,77	сс ( расхода-щийся 1111)
t р,С	77,9	68,6	67,1	102	308,8	ОО
I 1,(т/ч )•С	14,99	9,99	7,50	8,46	20,13	ОО
I 2,(т/ч)2 •С	5,98	3,44	2,45	2,18	3,39	ОО

Таблица 5

Показатели качества переходных процессов при k _р =2%хода ИМ /т/ ч и различных значениях T при возмущении по нагрузке

T ,c	5,0	7,0	10,0	13,0	15,0	17,0	20,0
ст,%	со ( расхода-щийся 1111)	63,41	28,98	9,24	0,19	0	0
t р,С	ОО	173,7	80,5	66,8	67,1	69,4	88
I 1,(т/ч )•С	ОО	15,56	8,23	7,20	7,50	8,49	9,99
I 2,(т/ч)2 •С	ОО	3,58	2,39	2,37	2,45	2,58	2,80

Таблица 6

Показатели качества переходных процессов при различных значениях k р ^иT при возмущении по нагрузке

k %хода ИМ k р,	1,0	1,0	1,5	1,5	2,5	2,5	3,0	3,0
T ,c	10,0	20,0	12,5	17,5	12,5	17,5	10,0	20,0
О,%	5,81	0	0	0	31,47	10,60	сс ( расхода-щийся 1111)	24,94
t р,С	57,3	114,9	54,1	82,6	115,4	98,9	ОО	202,7
I 1,(т/ч ) •С	11,03	19,99	8,33	11,66	9,68	8,09	ОО	13,54
I 2,(т/ч)2 •С	4,72	7,38	3,16	3,77	2,28	2,20	ОО	2,62

[2], включается инерционно-форсирующее звено

Изменение параметров объекта управления

Если робастность рассматривать как грубость системы по отношению к изменениям параметров объекта управления, то можно привести следую-щие результаты. Если все параметры объекта управления изменятся соответственно на А k об ,

АT,б и на Атоб , а регулятор будет иметь преж- нюю настройку, то передаточная функция разомк-нутой системы будет иметь вид

^T об ^p +¹

( T об ^{+ А T} об ) p +¹

и звено чистого запаздывания

(1 + Д k об/ k об )exp( "А^об p ) . Влияние инерционно-форсирующего звена на устойчивость САР и каче-:

если АT об < 0 и если |АT)б | увеличивается, то на- чинают преобладать дифференцирующие свойства

W ( p ) exp( ^Т°б p )

⁽9+т_об ) p

[ T >б ^p + 1](1 + Д ^k об / ^k об )exp(~^Атоб p )

( T )б ^{+А T} об ) p +¹

звена.

Если из (5) исключить передаточную функ-цию инерционно-форсирующего звена,т.е. если считать, что А T ,_б = 0 ‒ якобы постоянная времени

объекта управления не меняется, то , используя

Из (5) следует, что в данном случае после-довательно с «идеальной» передаточной функ-

критерий устойчивости Найквиста для систем с

запаздыванием, найдем, что критическая частота

цией разомкнутой системы, равной

exp(~%б p )

⁽9+т_об ) p

®кр

¹+ Д ^k об / ^k об 9+т_об

поэтому условие устойчивости замкнутой САР в :

(1 ^k об / ^k _Об)-2Й----2§-<л/ 2 .              (7)

9+тоб

На координатной плоскости « А k об/ k об ‒

Ат_об Лоб » граница области устойчивости будет

:

А ^k об   (1 j4%6)₁ ^k об 2(1 + Аб Лоб)¹

На рис . 2 изображена область устойчивости замкнутой системы при 6=0и А T _об =0.

На рис . 2 область устойчивости ‒ это область, расположенная ниже своей границы (штриховка направлена внутрь области). Как видно из рис. 2, даже при 9-0 замкнутая система обладает хоро- шим запасом устойчивости в отношении вариации параметров k об ^ Аб , причем, нетрудно видеть, что с увеличением параметра 9 область устойчи- вости замкнутой САР расширяется, так как

. । Гтс А I зет» вверх,а  —1+---- ‒ точка пересечения

22Тоб J кривой (8) с осью абсцисс « А тоб !^об » перемеща-ется влево . Следовательно , с увеличением 9 роба-стность устойчивости [5] повышается.

Понятно, что включение инерционно-форси-рующего звена с частотной передаточной функцией j™T>б +11+ со2T2

^j®(^T >б +А ^T 1б) +11+ со ²( T _)б +А T ,б) 2

х exp ^j arctg (® ^T >б)^_arctg(™( ^T _)б +А ^T )б ))])

изменит как критическую частоту, так и само ус-ловие устойчивости замкнутой системы, здесь со ‒ круговая частота, j=v~1. Критическую частоту юкр в этом случае необходимо отыскивать из ре-

:

(^{1     k} эб / ^k об ) м    ¹

(9 + Аб )®кр

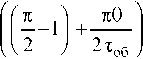
‒ точка пересечения кривой (8) с

осью ординат «А k об / k об » с увеличением 9 «пол-

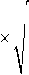
1,  22

^{1 +     T} )б

¹ + 0) ²р( ^T )б +А ^T )б)²

Решая это уравнение, получаем

_ ^0 _]_ ^ _ ^ 2 T 2 (¹+д ^k об/ ^k об)²

22        2-+

²(6 +Тоб) T ²,(¹ + АГ_об/ ^T )б)

²(9 + т_об) ^TЛ ¹ + АГ_об/ ^T )б)²

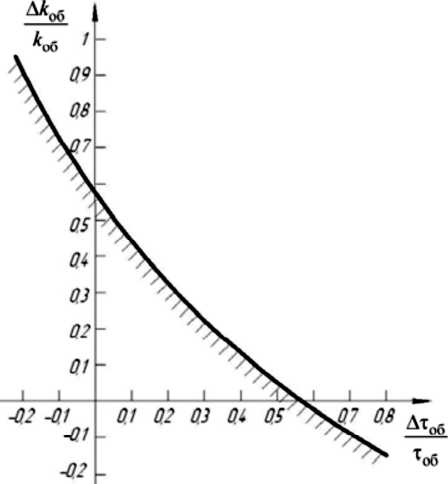
Рис. 2. Область устойчивости САР при 0 = 0и А T >б = 0

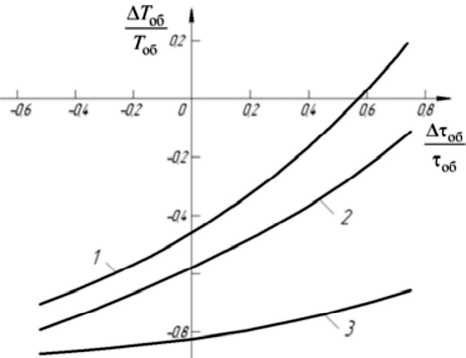
Рис. 3. Сечения области устойчивости САР при Л k об =0:

1 ‒9 =0с; 2 ‒9 =1с; 3 ‒9 =5с

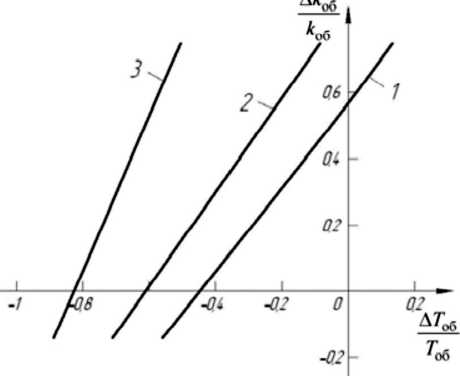
Рис. 4. Сечения области устойчивости САР при Атоб =0:

1 ‒9 =0с; 2 ‒9 =1с; 3 ‒9 =5с

Условие устойчивости замкнутой САР будет иметь вид

®кр^об (¹ "*" ^А^об /^об ) arctg (^юкр ^T й) +

+ arctg [®кр ^T >б ( ^{1     T} )б/ ^T )б)]<л/2.       (11)

Заметим, что соотношения (6) и (7) являются частными случаями условий (10) и (11).

Исследование границы области устойчивости САР, построенной по соотношению (11) с помо-щью среды программирования «Maple 10», пока-зало , что система имеет значимый запас устойчи-вости относительно вариации параметров объекта управления А k об ,А T >б ^{и Ат}об . Сечения границы области устойчивости плоскостями А k об = 0 И ^Атоб = 0 при 0 = 0; 1; 5 c приведены соответствен-но на рис. 3. и 4. Как видно из этих рисунков, раз-меры области устойчивости системы увеличива-ются при увеличении параметра 9 (увеличивают-ся размеры допустимых вариаций всех параметров объекта управления).

Как видно из рис. 3, неблагоприятное влияние времени запаздывания на устойчивость системы может быть скомпенсировано увеличением T _)б , что , в общем- , достаточно понятно . Из рис . 4 следует, что негативное влияние роста k об на ус-тойчивость САР также может быть нейтрализова-но увеличением T ,б .

Передаточная функция замкнутой системы по задающему воздействию при вариации всех пара-метров объекта управления А k об , А T >б ^{и Ат}об

:

^W С ( ^p)=(^T )б ^p +¹¹ +д ^k об/ ^k об) exp[ (^тоб^+Атоб) ^p ]х х{( ^T й ^{+ А T} й)(9+^тоб) p ² +(0+т_об) ^p+

+(^T й ^p +^{1 1}+д ^k об/ ^k об) exp[ (^тоб^+Атоб) ^p ]} ¹. (12)

Отсюда следует, что дифференциальное урав-нение замкнутой САР будет иметь вид

(T)б+АTй)(9 + тоб ) dd2x2(t) +(9+тоб) dx(t) dt2

dx (t Аб ^А%б) .

+T )б ( 1+Дkоб/kоб) dx t

+(1    ^k об / ^k об) ^x(^t Аб ^ААб)

^T )б ( 1    ^k об/ ^k об)

dx Д ^t ^об ^ДАб) dt

+(1   kоб/kоб)x3(t Аб ААб).

Решая непосредственно данное дифференци-альное уравнение (13) и используя программу рас-чета переходных процессов в САР, в которой ма-тематические описания элементов системы регу-лирования представлены по отдельности, устано -ВИЛИ, что при возмущении по заданию показатели качества переходных процессов при вариации па-раметров объекта управления будут следующими (табл. 7‒9). При этом считалось, что ПИ-регулятор имеет базовые настройки

T k >б =2%хода ИМ /т/ч;T,=T ,6 =15c.

* к k

Анализ данных табл. 7‒9 позволяет сделать вывод, что в окрестности точки (0,0,0) существу-ет довольно заметная область вариации парамет-ров Д k об ,д T >б ^{и А}Аб , для которой сохраняются приемлемые значения показателей качества пере-ходных процессов.

В табл. 10‒12 приведены аналогичные данные для случая возмущения по нагрузке.

Как это нетрудно видеть из (12), при отработ-ке единичного ступенчатого задания U ( t ) 1( t ) при t —^со x ->1, т.е. САР астатическая по задаю-щему воздействию. Передаточная функция сис-темы по каналу «возмущение со стороны регули-

Таблица 7

Показатели качества переходных процессов для k об = 1,5 Т/ч/%хода ИМ ; T >б =15c; ^Тоб 5c при возмущении по заданию при различных значениях А T >б

А T )б,c	+1	+3	+5	‒1	‒3	‒5
ст,%	0	0	0	0	0	2,11
t р ,с	45,2	46,0	45,9	44,0	54,6	68,8

Таблица 8

Показатели качества переходных процессов для k об = 1,5 T/ч/%хода ИМ ; T >б =15c; т_об = 5c при возмущении по заданию при различных значениях Лт_об

Атоб,c	+1	+2	+2,5	+3	‒1	‒2	‒3
ст,%	1,49	12,29	20,52	со ( эасходящийся ПП)	0	0	0
t р,С	64,4	129,1	272,3	сс	49,0	49,3	49,6

Таблица 9

Показатели качества переходных процессов для k об = 1,5 T/ч/%хода ИМ ; T >б =15c; т_об = 5c при возмущении по заданию при различных значениях А k об

k_     т/4     1 k эб,% хода ИМ	+0,1	+0,3	+0,5	+0,75	+1,0	‒0,1	‒0,3	‒0,5
О,%	0	0,31	2,61	9,70	сс (расходящийся 1111)	0	0	0
t р,С	42,7	55,3	54,7	130,8	00	46,4	49,0	51,1

Таблица 10

Показатели качества переходных процессов для k об = 1,5 Т/ч/%хода ИМ ; T >б =15c; т_об = 5c при возмущении по нагрузке при различных значениях А T_)б

А T )б,c	+1	+3	+5	‒1	‒3	‒5
О,%	0	0	0	3,49	12,40	25,06
t р,С	67,8	54,3	57,0	65,6	81,1	152,1

Таблица 11

Показатели качества переходных процессов для k об = 1,5 Т/ч/%хода ИМ ; T >б =15c; ^об 5c при возмущении по нагрузке при различных значениях Ат_об

Атоб,c	+1	+2	+2,5	+3	‒1	‒2	‒3
ст,%	21,83	43,50	54,19	со ( эасходящийся ПП)	0	0	0
t р,С	111,2	268,3	556,4	СС	62,7	63,2	63,6

Таблица 12

Показатели качества переходных процессов для k об = 1,5 Т/ч/%хода ИМ ; T >б =15c; ^об 5c при возмущении по нагрузке при различных значениях А k об

k_    т/ч 1 k эб,% хода ИМ +0,1 +0,3 +0,5 +0,75 +1,0 ‒0,1 ‒0,3 ‒0,5 ст,% 5,05 15,34 26,07 40,77 сс (расходящийся 1111) 0 0 0 tр,С 66,0 91,8 141,5 339,8 00 67,6 63,0 64,4 рующего органа ‒ ошибка регулирования» при базовых настройках ПИ-                     :

W ( p ) =( ^k эб +^{Д k} эб ) ^k эб ^T 6 ^p (т_об +9) exp(^об"*"^об) ^p ]х *{kT >б ^p (^6+ТобЖ ^T )б+д ^T )б) ^p +¹]+ +^T )б ( ^T >б ^p +¹)( ^k эб ^{+Д k} об)exp[ (%б^+Атоб) ^p ]} ¹ , (14) поэтому lim W ( p ) 0 при p 0, следовательно , по данному каналу САР также астатическая.

Заключение

Таким образом, достаточно подробный анализ показал, что рассматриваемый метод синтеза про-мышленных САР, позволяющий однозначно вы-брать как структуру, так и параметры настройки регулятора, обеспечивает приемлемое качество переходных процессов и достаточный запас ус-тойчивости системы при довольно заметных по размерам вариациях параметров объекта управле-ния и погрешностях задания настроек регулятора. Поэтому данный метод синтеза можно достаточно уверенно рекомендовать для практического ис-пользования.