К задаче о возмущении периодических решений дифференциальных уравнений с вырожденным оператором при производной

В банаховых пространствах Ei , E? в обозначениях и терминологии [1; 2] задача о ветвлении периодических решений при бифуркации Андронова-Хопфа с необратимым оператором при производной описывается дифференциальным уравнением

(1.1)

где A и Bq – плотно заданные линейные фредгольмовы операторы, N(A) = 8рап{ф^ , N*(A) = span^j}⁷^ ; N(B₀} = зрап{ф_к}^ , N*(B₀) = 8рап{ф_к}" – их подпространства нулей и дефектных функционалов, {^l}i , (Ф^еф = bp , {(Ж , {Mj} = ^lj ; {^s}l , , {^s}?, (C,si Фк) — ^sk – соответствующие биортогональные системы, ||ЖАо^)||=о(М) . Предполагается, что операторы A и Eq не имеют общих нуль-элементов, а также условия: 1°

ГА; с D\ и А подчинен ГА, т. е. Ь- А /лм || + .г на ГА:,, или Г) \:_ Dlll: и ГА подчинен .1, т. е. /VKIIM + ' на    , что позволяет свести обсуждение к ограниченным операторам.

В статье [3] дано применение уравнения разветвления в корневых подпространствах к рассматриваемым в [1] стационарным задачам о возмущении линейного уравнения малым линейным слагаемым и спектральных характеристиках линейного оператора, и соответственно в статье [4] - к рассмотренной в [2] задаче о ветвлении периодических решений.

Здесь исследуется ветвление чисто мнимых A-собственных значений оператора Г),, и отвечающих им периодических собственных элементов (периодических решений) линеаризованного уравнения при возмущении 1 > ( - ) оператора Г), ,

А А I BIBA (1.2)

в следующих предположениях [1], [5-7]:

1°. Число и является .4-собственным значением матричного оператора ./:(о), т. е.

В о а А

Во* «AJ

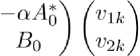
~ О, Г = [.и, с 2/;-мерным

—a A Bq подпространством нуль-элементов

АВА = чмфм = ("А , фМ = ( “Ч

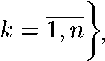
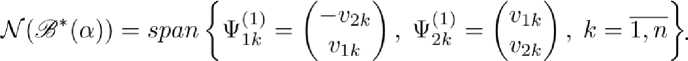
(1.3)

(1.4)

При этом числа +4i, Г -Д1.2.... не являются .4-собственными значениями матричного оператора ^(oj А 0.

, определенные равенствами

/ЛнФ'Д1 = АФ)) 11, .А А ) Ф'7 ' = А: Ф Д 1', имеют конечные длины щ. , т. е. образуют полный канонический обобщенный жорданов (.4-жорданов) набор (ОЖН) [1]. Без ограничения общности в силу разрешимости определяющих ОЖН уравнений это означает, что

ЛФД^У^-ЛФЛ^. А’У.АЛП-ФДЛ^ --1.ЖЖ. W-1.2. Г.1-[.и. (1.5)

или, эквивалентно, в координатной форме

(].б)

ЙМ*«2( ИЙММ’)> « = Ш Й1м*й И<ЙМ*4г > = ^^РР к,1^\,п.

В силу леммы о биортогональности обобщенных жордановых цепочек (ОЖЦ) [5-15] и линейности оператор-функций /-(о) к А и В Ри /А этот набор всегда может быть выбран триканоническим, т. е.

РР гр) = М*А- 1р> = а Фр11 "Г (z^, Фр) = М*А«

(1.7)

(1.8)

А =-4*Р^+1-’⁾, j=l,2, s(ff) = 1,рь(М М = Гп-или в координатной форме

(^UMr^) + MlU*^1^) = ws, ~ Н^ЛЙ5) + <а<+1Л^) = sklssa («ЙМ*^1-^ = ^А*^1-^ ~ (Au^1-^^) = (A^+1-Sb^.

Следуя [3], в этой работе далее исследуется уравнение (1.2) на основе кратко представленного аппарата обобщенных жордановых цепочек.

• 2.    Ветвление пары чисто мнимых A -собственных значений оператора B о

Выполним комплексификацию уравнения (1.2), рассматривая его в пространствах ‘--к А- ■ ^! к/- , /,■ — у 2, и учитывая, что оператор В[:) в силу его линейности также допускает достаточно гладкое расширение на эти пространства. Тогда элементы А = Щк + i Ак , йк и Vk = Vik + i Ак, А являются A-собственными элементами оператора в₀, т. е. собственными элементами следующих задач на собственные значения

Boiik = iaAu_k, Войк = —iaAuk, ВАк = —iaAAk, B^A = iaA*Vk, к = l,n. (2.1) Им отвечают А- и А -жордановы наборы (. 1- и А -ЖН = ОЖН), { н\! ¹}, {/у/ ) и { г'к ' }, { г'к ' }, в которых обобщенные жордановы цепочки определяются уравнениями ¹ А<~/<А ) /А = А/ ¹ , UWHU)p-'^; = - Ц/ ; Рр + тЛАг-^-РАу' ; (/р-жЖ )^^: = . Г р/ ; ./-2^ , k — \ .п , и соответственно (1.7) и (1.8) могут быть выбраны удовлетворяющими условиям биортогональности

:«к-к- = ^- ^к.,^^^^^ А = л"к ' "- <'■ = .•!■•!'■" '■.   (2.2)

Выполнением подстановки А. Пуанкаре I      , AD= АА, где I1 = кА) - подлежащая определению малая добавка к частоте колебаний, задача (1.2) сводится к определению Зл-периодических решений уравнения

В.!/ (Afi AAh ^ Ш^Ат} В^А)        Ан [A IDA)         (2.3)

ат                  ат

Здесь предполагаемый фредгольмовым оператор [At А А и остальные операторы отображают пространство J 2 тг-периодических непрерывно-дифференцируемых функций Т со значениями в А = A i Е\ в пространство 3 2тг-периодических функций т со значениями в Е — 1'. 2 i / /-2. Дуальность между J и Е (3 и Зо определяется специального вида функционалами

1     /•27Т

«у, Ы = тг ^ ^т^ УЕУ^ / Е Е (У ^zj^za

Подпространства ЛЕп К -ЕЕ₍) нулей операторов LA и Рр 2п-мерны

Я{В^ = 8рап{^} =^к1\т)=икегт, рк}}к=1, ^В^зрап^ = ^кЧт} = гкВАВк}}к=\ биортогональные им элементы выбираются как Г- и 1-образы последних элементов ОЖЦ ■' ' Е' = Eq.' ( = 2* и ' г/ — ' "/ д' = J1 . Отвечающие базисным элементам подпространств -ЕЕ) и ЛЩД ОЖЦ имеют вид 34' = tpA A f'^^AB^’’ с соответствующими условиями биортогональности

«»>W» = ^- ЗРЗЗ = w^

7^ = T = A*v^⁺¹~^e^ir, z^ = 2^3^Т = А^^к+1~^з)З^т

Лемма 2.1. [6; 8-10] Соотношения биортогональности (2.4) определяют проекторы

Р = ЕЕ^^Е^ = ЕЕМ Р = EW, Р = Р+Р : £1 ^ Ак = К^В.А) = sp0,n{p,p}: n Pk ъ = ^ТЛа^а^^ qmmm q = q+q: E ^ E,2K — -span^z^, г]? Д, A—i 7=1

где 3  (г/                     ААеА векторы Д си : определяются аналогично, порождающие разложения пространств t\ и 2 2 в прямые суммы l’i Е '   1'   - '

Е ~ Агк i <2 \ 2К, А — А /д - корневое число.

S=1

При этом справедливы соотношения сплетения

ЕЕ - QE , ЕР QE _На l)№\ IP = Q I , IP Q I на Щ.Ц

\0 1 ... о/

.

/о о ... 0\ 0 0        1

с Pk -кре-ккемиами вк —

Операторы 1 и С., действуют в инвариантных парах подпространств , А, Д :1. и

Е ^А, Е х ;к;В^Врр А^ ^Ас_ ₂к,Л : 8 1 ^л ^ Е.2Л являются изоморфизмами.

Вводя регуляризатор Шмидтайо = ^о+ Е(С7?Ы1)+ ^(G^W, запишем fe=l                   fc=l уравнение (2.3) в виде системы

(2.5)

fe=l

Полагая у = w + v ,                    , находим

Bo™ + £ £ ^kj^o^ + ^kiB0^ ) - y^'w - B^w =

= м E E(sk/^ ^} + ^^^) + E El^Bie)^ + ^k^ k=lj=l                       k=lj=l

Обращая оператор Bq ,V=r₀ [1], получим

W - yV^W - Г0В(е)ш = - Ё E ^kj^ + Ik^) + У^^ Ё E (F^ + ikj^^ k=lj=2                        k=lj=l

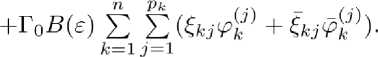
Отсюда следует

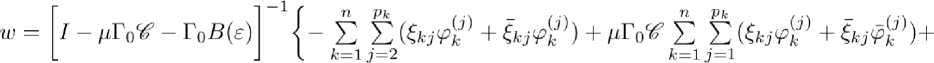
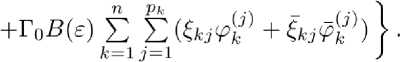
Далее [_Z _ ^Го^ - ГоВ(е)]-¹ = [I - (I - MW^roWFV - A*W\ [I _ ^r₀^ - ГоВ^гЯвй = [! (/- ^ГоЯ^ГоВ^)]-¹^ - аЯЯ ’EBUl = = (/ - ЖЯ^ГоВ^Ж - Г₀В(£)(/ - /ЯЖИГоВИ’¹ и

I k=\j—2                            k=lj=l                   J

- Ё Ettkj^+^b + ^^^ k=lj=2                                      k=l

Следовательно,

n

Wfi'^ E E{^г^У + ^kj^) ]  |/ /'l i/^ ВДс")] 1Г0В(е) E E ^kj^k + ^iVk^) — k=lj = l                     J                                     A-1.7 = l

- E EM’+Wl;'')+

- Ж^да-МН’1

A—1 J=2

+(^ - /В o^)-1/^!^^ E GF^fc1) + чнИ-1)) +

+(/ - FoF’F - r₀BF(z - mWTFbf £ £ ж4^;) + ^Ь -

/с=1 J = 1

= -E Effe^MW’)- fc=lj=2

-[i - (i ~ ^^Г^ов^^            £ £ Ч;£: । чЧ’| । k=lJ=2

+[/-(/- мГоЧ^ГоВЧГЧ/ - MwRr0^ £ (^1^ + W^R w =[/-(/- рГо^-^оВ^-Ч - ЖоЯ-1

- E '?/  '..

k=lj=2

+7 - (/ - ЖоЯ^ГоВЯГЯ - ^o^-RoBfe) £ £ Йу^ + Ь^Ь -

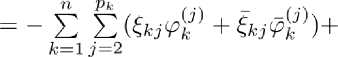
+ [/-(/- RoR-RoBR]-¹^ - AJW-Rro^ £ (^i^ + W^R

+ [/ - (/ - ЧЪЧ^ГоВЧГЧ/ - уГоЯ^ГоВЯ £ Ri^ + W^)

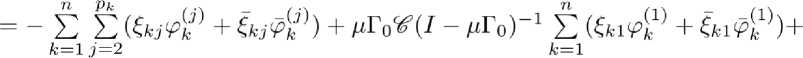
+(/ - /ПЖИВДеЖ - a - RRRroBHR/ - yWRr^ £ Ч^’+^^^Н

+4 - ^oR-RoBR^ -(I- да^ГоВИ]-¹ £ Ri^ + W^) =

£ £ tt^ + ^Ь + RoW - MW¹ £ (W^ + W^R fc=lj=2                                               fc=l

+(/ - /ЖЖЧВДеЖ - (/ - ЖоЧНГоВНЛ/ - mW¹ £ (W^ + W^)-

(2.6)

Формулы

Го^ = гГ0В0^2) = г^2), (ГоЯ2^ = ЯГоЯ^2) = *МЛ • • •

(ГоЯ*^ = «Vfc⁺¹⁾ при s <Рк , (ГоЯ^Я^ =^4^,            (2.7)

Ф 9;S S^S [l^>k'\^{Pk +} ^                 у (1)               I (s)         (Pfc+l —s)

Ц о Я Ж - 1 ^k         при S > Vk, '^к — ГоЖ , Я- — £л , определяют выражение

ЖоЯ/ - AiW1 £ ^1^П + ^l^) =

(2.8)

Я-Д*¹^ к-^у^Р + (-яй²⁾ + • ■ • + HpR-RM-

Теперь подстановка у = W + £ ^ + £ ^ во вторые равенства системы (2.5) в силу соотношений (2.4) при условии принадлежности присоединенных (корневых) элементов сею—2п                             Г           -Cl Т Т Т Т        Л Л прямому дополнению ^1    к подпространству собственных элементов ^1 и учете формул

(2.7),  (2.8) дает линейную однородную разрешающую систему (аналог уравнения разветвления в корневом подпространстве), состоящую из уравнений

tkiM = Чи^ - W-^r0)-W) [/н^ - M^roHiW)] 1 • Д 1_(^ й11 + ^^к}+• • • + ы^-1^^

+ !_(^ [^ + (-^)Й2) + ■ ■ • + (-^'"VM’ 4П^ = °1 tka^,е) = ^ - ^^^ - «а - ^r0)-w) [/-(/- ^Гог^овд]

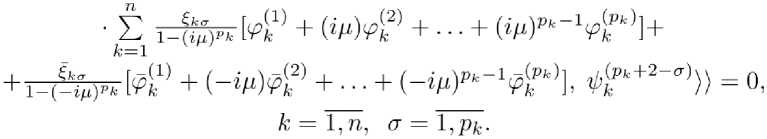
(2.9)

и соответствующих им комплексно-сопряженных, равенство нулю определителя которой является уравнением разветвления в корневых подпространствах для определения периода колебаний ск+р , М = 1^) , возмущенной задачи (1.2).

Замечание 2.1. В линейной однородной разрешающей системе слагаемые в уравнениях и им сопряженных, содержащие двойственность, можно записать в виде

Ш - //«То)-1 [/-(/- Ayi-T.BH]{...},Йр-+2-”>)) == «[/-(/- /ЗД-'ГоВИ]{...}, (Z - //ГЭТ-М^2-”)), и учитывая, что Q*  —у4* , выразить компоненты

(I - ^г^*)-1^^2"^, (/ - ^^Г1'^?^2-^

через линейную комбинацию ОЖЦtf⁵,^,-,^-, соответственно ^ч<ч...,^ .

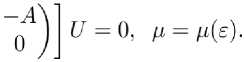
(3.1)

Следует выяснить как изменится >/4 —

О -А

А О

-собственное значение а оператора

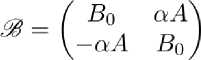
при возмущении в(а) оператора ^о. Таким образом, рассматривается

задача на собственные значения

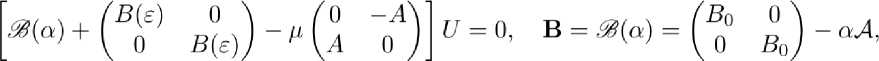
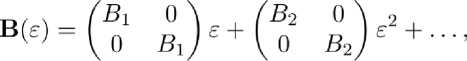
т. е.

^(a)U = [-В(ф + fiA]U = O или В?7 = - В (ер + _fi AU, U ={  ) •   (3.2)

*i = (*L *L - ■. , ■ ■ ■,

+B(0 p + E E(^B^+^B<)j = Е^РЙ+^Й. (3.3) \ k=lj=l                        / fc=l

& = <^ rg) = W rg?) + E E «*8? + W). ri), i = 1,2.

Обращая в первом уравнении оператор В, получаем

A:=lj=2                          k=lj = l

Так как[I - fiTA + ГВ(е)]-¹ = [!-(/- pAEPB^pV - PA)”¹и

<^) + мГД(1 - PA)-1 E (^< + f^^), следовательно

(3.4)

Подстановка определенного по формуле (3.4) w во вторые уравнения системы (3.3) при учете формул

^14 ГВФ!^ = Ф^, (ГЛ^Ф^ = Ф*^,     (гл^ф¹^ = ф^⁺при S < Рк:

при

(w «‘V = ф^11 = ф« r^’W ~ гвф^ — ф^А (гд^ф^? = ф^, ..., (гл)5ф^ = ф^ )при S < Рк:

при

(ГД)^^^ = Ф^+1) = Ф^, как и ранее, дает однородную систему 2К-порядка линейных алгебраических уравнений, равенство нулю определителя которой является уравнением разветвления в корневом подпространстве относительно М = ^£).