К задаче параметрической идентификации математической модели теплового режима зданий

В нашей стране на теплоснабжение зданий расходуется более одной трети всего добываемого топлива, причем основными при этом являются затраты на отопление. В связи с этим даже относительно небольшой успех в решении проблемы энергосбережения при отоплении зданий, в силу масштабности энергозатрат, приводит к ощутимым эффектам в абсолютном выражении. Известно, что наибольшая экономия тепловой энергии в системах теплоснабжения достигается за счет их автоматизации. Поэтому разработка вопросов, связанных с автоматизацией систем отопления и их совершенствованием, является вполне актуальной проблемой. При этом следует иметь в виду, что первоочередной задачей, которую необходимо решать при разработке высококачественных систем управления, является создание соответствующего математического и программного обеспечения, в частности, динамической математической модели температурного режима зданий и алгоритмов ее параметрической идентификации. Объясняется это тем, что как сама структура системы управления, так и параметры ее настройки определяются, прежде всего, свойствами и характеристиками объекта управления, которые, в частности, и представляются математической моделью. Вместе с тем свойства и характеристики заметно меняются, например, из-за старения здания, при накоплении влаги в ограждающих конструкциях и т. п. Поэтому вполне понятно, что необходимо своевременно отслеживать изменение этих характеристик, т.е. решать задачу идентификации математической модели, причем лучше всего это делать с помощью адаптивного алгоритма, отличающегося достаточной оперативностью.

Известно [1, 2 и др.], что тепловой режим зданий удовлетворительно может быть описан следующим дифференциальным уравнением:

dtВ (т) , . dtн (т) , . , .

тв з + tв (т) = TH 3 + tн (т)+kпWСo(т),(1) dт dт где tВ (т), tН (т) - соответственно температура внутреннего и наружного воздуха; ТВ, ТН - соответственно постоянные времени для внутреннего и наружного воздуха; WСО (т) - мощность системы отопления; т - время; кП - коэффициент передачи, причем кП = 1/ (qVV). Здесь qV - удельная тепловая характеристика здания; V - его объем.

Адекватность данной математической модели достаточно скрупулезно установлена в работах [1, 2], вместе с тем представляет интерес разработка и других (не только представленных в [1, 2]) вариантов процедуры параметрической идентификации модели. Здесь могут быть найдены некоторые предпочтительные для различных условий решения. В частности, как это уже отмечалось, интересны адаптивные алгоритмы параметрической идентификации, так как они позволяют оперативно отслеживать изменение характеристик объекта. Кроме того, из соотношения к П = 1j ( q V V ) следует, что, сконструировав адаптивный алгоритм оценки коэффициента передачи к _П, мы тем самым решим и проблему определения и удельной тепловой характеристики q_V , являющейся важнейшим интегральным показателем качества теплозащитных свойств зданий, указываемым в их энергетическом паспорте. Поэтому рассмотрим адаптивный алгоритм оценки всех параметров модели (1), в том числе и параметра к _П .

Задача адаптивной идентификации формулируется следующим образом. Пусть известны оценки параметров в i -й момент времени - T _{B i} , T_Hi ,

Соотношения (3)-(6) содержат производные сигналов температуры внутреннего и наружного воздуха по времени, как известно, проблема помехоустойчивого дифференцирования сигналов не является простой, здесь, очевидно, необходима определенная проработка конкретного способа реализации процедуры дифференцирования.

Конечно, можно применить самый распространенный и, на наш взгляд, самый простой способ уменьшения влияния помех при дифференцировании - это предусмотреть низкочастотный фильтр в виде инерционного звена первого порядка. Однако, как нам представляется, предпочтительнее использовать алгоритм, приведенный практически без пояснений в [3]. По нашему мнению, обоснованность данного алгоритма следующая.

Пусть средняя величина сигнала в ( i + 1) -й момент времени определена по четырем точкам, т. е.

x = ( x i + 1 ⁺ x i ⁺ x i - 1 ⁺ x i - 2 ) /⁴ . i⁷)

Отнесем x к середине временного интервала, на котором располагаются рассматриваемые точки, т.е. картина расположения точек будет такой, как это представлено на рис. 1.

x i + 1

кПi, пусть, кроме того, для (i +1) -го момента вре- мени получена новая информация с объекта управления

dt в ^(т i + 1)     „ (            dt н ^(т i + 1)

i - 1

d т     ’ tВ ':-) ’        d т tН (тi+i), Wco (тi+i). Ставится вопрос: как, зная оценки параметров для i -го момента времени, по новой информации с объекта управления найти новые улучшенные оценки этих же параметров -Тв(i+1), Тн(i+1), кП(i+1) ? При этом понятно, что кри- терий идентификации должен иметь следующий вид:

I ( i + 1) =

T В i

dt в ( т + 1 ) d т

⁺ t В ^(т i + 1 ^)- T Hi

^dt Н ^(т + 1 ) d т

-

т i - 2                    i - 1                      i                     ч + 1

Рис. 1. Расположение точек, используемых при дифференцировании

t Н ^(т i + 1 ) ^к П 1^WCO ^(т i + 1 ) ] .                    ⁽²⁾

Решая задачу методом наискорейшего спуска, получаем:

dt p (т,-,,

TB(i+1) = TBi- 2h •[•] В; i+1) ;(3)

( )

d t-ц т,-

TH(i+1) = THi + 2h •[•] H; 1+1);(4)

( )

кП(i+1) = кПi + 2h • [WСО (тi+1 ) , где под [•] понимаются квадратные скобки из (2)

Очевидно, что в этом случае можно пользоваться следующими четырьмя оценками производной:

со всем своим содержимым, а шаг h определяется из условия достижения минимума критерия (2)

dx ^(т i + 1 ) ^ x i + 1 ^{- x} .

d т       1,5 Ат ^;

^{dx (т} i + 1 ) _ x i ^- x .

d т     0,5Ат’ dx (т1+1 ) „ x - Xi-1 .

dт      0,5Ат ’ dx (т i+1) _ x - xi-2

d т       1,5 Ат .

при движении в антиградиентном направлении:

Здесь Ат - промежуток времени между моментами считывания сигналов Ат = т _{i + 1} - т _i , i = 0,1, 2,.. .

h =

^dt в ^{( т} 1 + 1 ) d т

^dt н ^{( т} 1 + 1 ) d т

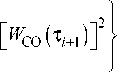
. (6)

Понятно, что лучшей оценкой будет среднее

арифметическое найденных величин, т. е.

dx ( т + 1 ) d т

^xi + 1 ^{- x} + ^xi ^{- x} + ^{x - x}i - 1 + ^{x - x}i - 2

1,5 Ат    0,5 Ат   0,5 Ат    1,5 Ат

Панферов С.В., Панферов В.И.

Ат

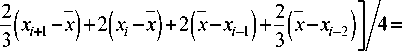
1 1/

— 7 ( x + 1

Ат 6

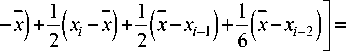
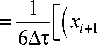
- х)+3( х, - х) + 3( х - хг-1

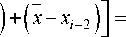
I x + 1 ^{+ 3} x - ³ x - 1 - x - 2 ] . ⁽¹²⁾ 6 Ат

Данная формула для вычисления производных приводится в [3, с. 161]. Апробация алгоритма проводилась следующим образом.

Для конкретного здания с конкретной системой отопления отыскивалось решение дифференциального уравнения (1) для некоторой заданной функции t _Н ( т ) . Далее на полученное решение

накладывалась помеха, генерируемая с помощью датчика случайных чисел. Затем этот зашумленный сигнал t В ( т ) использовался для отработки

приведенного адаптивного алгоритма идентифи-

кации параметров, при этом исходные численные значения идентифицируемых параметров задавались существенно отличными от тех их значений, которые содержались в решении дифференциаль-

ного уравнения (1). Производные

dtв (т/+1) d т

dtн (т/+1) d т

вычислялись по формуле (12). Анализ

полученных результатов показал следующее. Алгоритм идентификации в виде соотношений (3)–(6) удовлетворительно отслеживает изменение численного значения параметра k _П , численные

ся неявно в решении дифференциального уравнения (1), составляло 3,103 •Ю ^{- 5} °С/Вт. Начальные значения параметра k _П , как это видно из рис. 2, составляли 2 •Ю ^{- 5} и 4 •Ю ^{- 5} °С/Вт, причем начальное значение к П = 2 • 10 5 °С/Вт исправлялось как по данным без помех, так и по данным с помехами.

Как видно из рис. 2, коэффициент передачи k _П исправляется с помощью адаптивного алгоритма в целом достаточно быстро, только при наличии помех в экспериментальных данных наблюдается некоторое колебание его текущего значения вблизи истинного значения к П = 3,103 •Ю ^{- 5} °С/Вт.

Если считать допустимым отклонение температуры внутреннего воздуха от своего заданного значения в 0,5 °С, то погрешность определения параметра k _П не должна превышать при мощности системы отопления W _co = 1,74 •Ю⁶ Вт значения 0,0287 •Ю ^{- 5} °С/Вт, если же допустимо отклонение в 1 °С, то погрешность оценки параметра к _П может быть увеличена до 0,0574 •Ю^-5 °С/Вт. Конечно, все это еще зависит и от уровня помех, действующих на объекте. Поэтому для большей точности оценки параметра k _П в схему обработки экспериментальных данных помимо помехоустойчивого алгоритма дифференцирования (12) включили еще и предварительный алгоритм фильтрации сигнала о температуре внутреннего воздуха.

Задача фильтрации сводилась к следующей задаче оптимизации:

V 1 ( x ^- x Ф ) ^{2 +} V 2 ( x Ф ^- x Ф1 ) ² ^ m i n, ⁽¹³⁾ x_i Ф

значения постоянных времени T _В, T _Н восстанавливаются значительно хуже. Вероятнее всего, причиной этого является то, что скорость восстановления различных параметров (величина коррекции параметров за один шаг), заложенная в соотношениях (3)–(6), совсем разная: для T _В, T _Н

. .    „ ~               _ ^dtB ^(т ' + ¹ )

она прямо пропорциональна 2h •[•]-------- и d т

4 7     dtН (т/+1 )      „              ,               „

2 h • [ •]---------- , а для    к_п    - величине

d т

2 h • [ • ] W со ( т + 1 ) . Очевидно, что W co >> dt ⁵, dt ^H. d т d т

Поэтому и имеет место данный факт. Вместе с тем необходимо иметь в виду, что для реализации концепции построения адаптивной системы необходимо оперативно отслеживать только численное значение параметра k _П , что позволит корректировать величину удельной тепловой характеристики здания q_V . Для примера на рис. 2 приведены кри-

где x – фактическое значение сигнала в -й момент (отсчет); x Ф – оценка полезного сигнала для -го момента времени; V 1 и V ₂ — весовые коэффициенты.

Решая данную задачу оптимизации, нашли, что оптимальная оценка полезного сигнала должна определяться по следующей формуле:

Ф V 1 X / +V 2 x Ф x =------:------

.

V 1 +V 2

Удобно данное соотношение записать в следующем виде:

. ф _ ф ,     У1

вые, иллюстрирующие процедуру отслеживания параметра k _П как при отсутствии, так и при наличии помех в исходных данных. При этом истинное значение коэффициента передачи k _П , содержащее-

V 1 ⁺ V 2 ^х '

Данный алгоритм позволяет отслеживать изменение полезного сигнала во времени. Как видно из последнего уравнения, если сигнал не изменился за промежуток времени между ( i - 1) -м и i -м моментами, то оценки х, ^Ф и х, Ф - 1 будут совпадать.

В условиях действия случайных помех, как известно [4], численные значения весовых коэффициентов V i и V ₂ следует выбирать так, чтобы

V 1 ₂, так как при наличии помех невязка х , - х , ^Ф обуславливается в основном помехами,

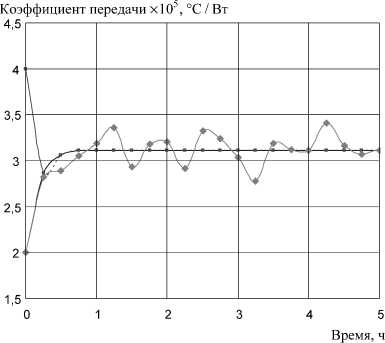
Рис. 2. Отслеживание численного значения параметра k _П

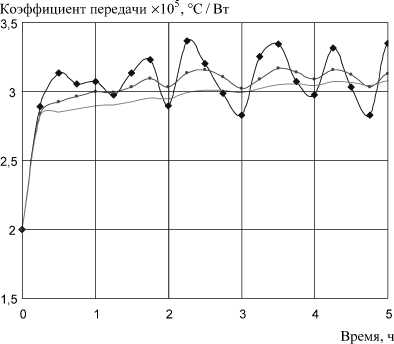
Рис. 3. Отслеживание численного значения параметра k _П при использовании алгоритма фильтрации

накладывающимися на результаты измерения. Таким образом, нужно достаточно осторожно относиться к новой информации x_i , большее значение следует придавать прежней информации х Ф - 1 , конкретные значения у 1 и у 2 , естественно, должны учитывать реальную статистическую ситуацию на объекте. Опыт применения данного алгоритма показал его пригодность для фильтрации сигналов. Для примера на рис. 3 приведены кривые, иллюстрирующие работу алгоритма: кривая 1 – это оценка параметра k _П при отключенном алгоритме фильтрации (15), кривые 2 и 3 – оценки, найденные по формуле (5) с включенным алгоритмом фильтрации соответственно для у 1 = 0,3;

у 2 = 0,7 и для у 1 = 0,1; у 2 = 0,9 . Кривую 1 можно рассматривать как оценку, найденную для у ₂ = 0 .

Как видно из рис. 3, алгоритм (15) обладает заметными фильтрующими свойствами, по временному признаку его следует отнести к алгоритму запаздывающего оценивания [5], что вполне объяснимо, поскольку алгоритм по характеристикам близок к инерционному звену первого порядка (экспоненциальному сглаживанию первого порядка) [5, 6]. При этом, как и следовало ожидать, уменьшение у 1 и увеличение у 2 приводят к усилению как фильтрующих, так и запаздывающих свойств алгоритма. Отклонение получаемых оценок от истинного значения k _П заметно уменьшается. В наших расчетах это отклонение всегда удавалось за счет настроек алгоритма фильтрации (за счет выбора у 1 и у ₂ ) довести до допустимого значения. Таким образом, дополнительное использование алгоритма фильтрации позволяет получить вполне работоспособную процедуру оценивания коэффициента передачи, а равно и удельной тепловой характеристики зданий.

Выводы. Разработан адаптивный алгоритм параметрической идентификации математической модели теплового режима отапливаемых зданий. Настроенная на «реальный процесс» математиче- ская модель может быть использована как для исследования особенностей теплового режима, так и для разработки высококачественных управляющих устройств, в частности, для настройки погодного регулятора в системах отопления [7]. Кроме того, найденное по экспериментальным данным значение удельной тепловой характеристики позволит оценить реальные теплозащитные свойства здания, что имеет весьма важное значение при оценке энергетической эффективности здания и разработке энергосберегающих мероприятий.