Качественное описание математической модели для процесса деформации при прямоугольной раскатке колец

• ¹    Самарский государственный аэрокосмический университет

• ²    Самарский металлургический завод

В статье описана модель для процесса деформации при раскатке колец в прямоугольных калибрах. В основу модели положен метод конечных элементов. Рассмотрены особенности задания граничных условий для раскатки колец при использовании метода конечных элементов.

Номенклатура изделий, получаемых раскаткой в различных отраслях машиностроения, постоянно растёт. Это ставит перед производителем проблему быстрого освоения новых изделий, что требует более глубокого понимания механики процесса. Достаточно сказать что в процессе, где используются валки не равных диаметров из которых один приводной даже задача определения геометрического очага деформации оказывается сложной. Часто при проектировании используется большое количество предположений и эмпирических зависимостей. Такой подход пригоден лишь для ориентировочных расчетов и не обеспечивает требуемой точности. Для получения более глубокого и точного понимания процесса необходимо применение методов математического моделирования.

Исходя из того, что очаг деформации имеет сложную форму будем использовать метод конечных элементов. Целью данной работы, является разработка математической модели технологического процесса горячей раскатки кольца позволяющая составить представление о геометрических и силовых процессах в очаге деформации.

Для снижения объёма вычислений в качестве объекта моделирования выберем раскатку кольцевого сегмента, рис.1 вместо раскатки кольца. Длину сегмента до обжатия принимаем 6 длинам очага деформации. Длину очага деформации оцениваем по формуле А.И. Целикова [1]

Ld =

2( A h )

1и

R 1 R R R

HB 2

где R ₁ , R ₂ – диаметры приводного и не приводного валков, R_H , R_B – наружный и внутренний диаметр кольца, a h - абсолютное обжатие.

Моделирование ведется по оборотам кольца. Каждый из оборотов включает следующие шаги :

• -    расчет геометрических параметров сегмента с учетом изменения положения валков за время оборота и подготовка конечноэлементного разбиения.

• -    моделирование раскатки сегмента (рис. 1).

Моделирование прокатки сегмента проводится по временным шагам. На каждом шаге производится расчет напряженно-деформированного состояния методом конечных элементов. Считаем, что после прокатки 3 длины сегмента достигается состояние очага деформации близкое к установившемуся. Выбираем сечение на расстоянии Lg от выходного сечения геометрического очага деформации, сечение АВ на рис. 1. Для данного сечения определяем толщину кольца, распределение напряжений на толщине σi,j(XAB) , XAB– координата по высоте сечения.

Решение проводим в условиях плоской деформации, используем стандарт-

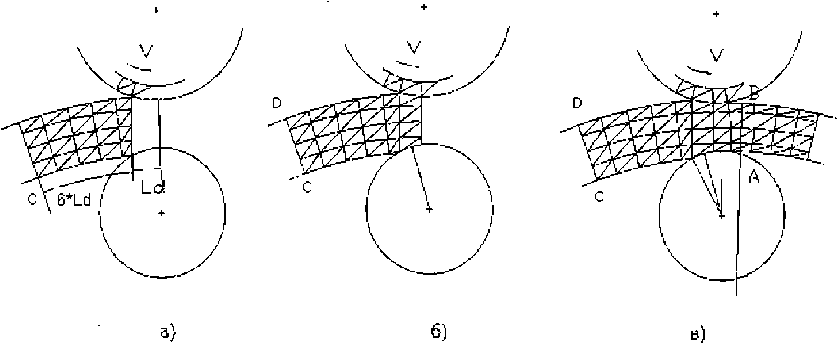
Рис. 1. Фазы моделирования процесса раскатки сегмента:

а – при начальном положении;

б – при первом шаге; в – при установившемся очаге деформации

ную процедуру метода конечных элементов [2]. Адекватность расчета моделируемому процессу достигается заданием граничных условий.

На части сегмента CD, рис.1 накладываем ограничение на перемещение узлов. Перемещение происходит по окружности, центр которой смещен на Ld от линии осей валков по горизонтальной оси. Радиус окружности для точек на верхней поверхности кольца Rн, для нижней поверхности Rв для внутренних точек на СD радиус меняется линейно между указанными граничными значениями. Для узлов, которые перемещаясь через очаг деформации, в ходе моделирования, достигли осевой линии валков, задается ограничение на движение по окружностям с центром на осевой линии валков и радиуса-

ми увеличенными на

RН

- R_В

RН

-

R В

- Δh

по срав-

нению с условиями на CD. Таким образом достигается учет действия отброшенных частей кольца.

На первых шагах решения принимаем, что верхние и нижние угловые точки сегмента находятся в контакте с валком и перемещаются вместе с точками поверхности валков рис 1а.

После достижения контакта двух узлов с поверхностью верхнего приводного валка для данного узла может существовать два условия трения. Трение покоя, когда узел движется вместе с поверхностью валка, и

сухое трение по закону Прандля с коэффициентом µ . Первоначально точки находятся условиях трения покоя, в качестве граничных условий задаются и перемещения. Для определения условия перехода от одного вида трения к другому (после определения напряжений и перемещений на данном шаге) анализируем расчетные величины нормального P и касательного τ напряжений. Если в момент нахождения узла на предыдущем шаге выполняются условия трения покоя, то при µ P <  τ переходим от задания перемещения в данном узле к заданию силы равной µ P .

Когда точка движется от входа в очаг деформации, происходит первое изменение условий трения и направление действия силы совпадает с направлением вращения валка. Второе изменение, происходит когда точка движется к выходу, и сила имеет противоположное направление. В случае нахождения узла в условиях сухого трения анализируем перемещение. Если перемещение отличается на некоторую, заданную малую величину от перемещения валка переходим к заданию граничного условия в перемещениях, точка движется с валком.

Для нижнего, неприводного, валка скорость вращения не известна. Она находится путем последовательных приближений на каждом из которых производится решение конечно-элементной системы уравнений. Ус-

ловием завершения расчета является равенство нулю момента сил, действующих на не приводной валок со стороны полосы.

Выводы

Предложена и описана математическая модель процесса деформации при раскатке кольца. С помощью выбора описания геометрии моделируемого объекта и постановки граничных условий обеспечено адекватное описание процесса при сведении вычислительных затрат к приемлемому уровню.