Качество динамики кругового газостатического подпятника с опорным центром на упругом подвесе

Известно, что газостатические подпятники с кольцевыми диафрагмами абсолютно устойчивы [1], однако качество их динамики имеет ряд серьезных недостатков. К их числу относится низкое быстродействие, повышенная колебательность переходных процессов, большие амплитуды резонанса частотной характеристики передаточной функции динамической податливости. Это объясняется негативным влиянием заключенного в несущем слое объема сжатого газа на демпфирование подпятника.

Улучшить динамические характеристики подпятника можно посредством усовершенствований, направленных на уменьшение объема несущего смазочного слоя и повышение его демпфирующей способности.

На рис. 1 показана схема кругового газостатического подпятника (ГП) с валом 1 и основанием 2, которое соединено с опорным диском 3 радиусом r ₀. ГП питается смазкой от источника сжатого газа через отверстия малого диаметра d , которые равномерно расположены на диске 3 по окружности радиусом r 1 . Центральный опорный центр 5 поддерживается упругим подвесом 4 в виде тонкого кольца толщиной δ, обеспечивающего необходимую величину деформации e материала диска 3.

Во время работы подпятника смазка подается в него под давлением pH через отверстие в основании 2, далее через кольцевые диафрагмы попадает в несущий слой и затем истекает из него в окружающую среду. Под действием разности давлений pH - pd > 0 на поверхности

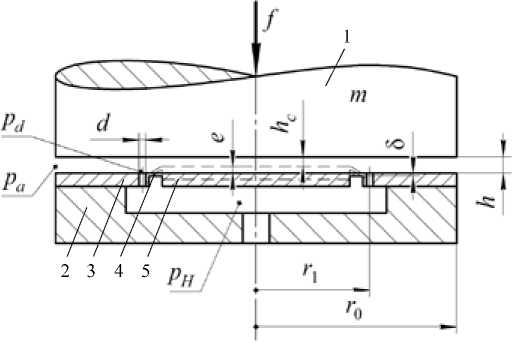
Рис. 1. Расчетная схема подпятника

Fig. 1. The design scheme of the thrust bearing опорного центра 5 происходит деформация кольца 4, вследствие чего этот центр смещается на величину e в направлении вала 1. По сравнению с обычным подпятником (e = 0) в таком ГП объем газа, заключенного в его несущем слое, будет меньше, кроме того, вследствие деформации материала кольца 4 изменится характер колебаний несущего слоя смазки, что может способствовать повышению качества динамики конструкции.

Математическое моделирование

Исследование качества динамики ГП проведено в безразмерной форме. Размерные величины математической модели обозначены строчными буквами, безразмерные – прописными. За масштабы безразмерных величин приняты: наружный радиус r ₀ - для радиусов; соответствующая расчетной статической нагрузке f₀ (стационарный режим «расчетной точки») толщина h о слоя смазки на наружном кольце диска 3 - для перемещений и смещения e , давление pa окружающей среды ^— для давлений, ^п r о ² pa ^— для сил.

Математическая модель описывает движение сжатого газа в областях смазочного слоя, образованного поверхностями вала 1 и центра 5 (центральная область 0 <  r <  r j ), наружного кольца диска 3 (кольцевая область r 1 <  r < 1). Области соприкасаются по окружности радиуса r 1 , ^на которой расположены кольцевые диафрагмы.

Функция давления в смазочном слое этих областей подчиняется системе (1) – (2) краевых задач для дифференциального уравнения Рейнольдса [2]

—I RH 3 P_c ^ c | = о R d R I       d R )

d ( PH ) c T

^ = 0, ^Pc ( ^R 1 ,T) = ^Pd (T), ^P ( ^R ,0) = 1,

d( PH)

S t

[ Pr (Ri ,t) = Pd (t), Pr (1, t) = 1, Pr (R, 0) = 1, где Pc(R, т) и Pr(R, т) - функции давления в смазочных зазорах областей; Hc(т) и H(т) - функции толщины зазоров в этих областях; Pd(τ) – функция давления на выходе кольцевых диафрагм; R,

τ – радиус и текущее время. Здесь

а = 12//Г ph t 0

- «число сдавливания» газового слоя [3], где ц - динамическая вязкость газовой смазки, t о -масштаб текущего времени.

Для определения неизвестного давления Pd (τ) использовали уравнение неразрывности смазочного потока

Q r (т) - Q c (т) = Q d (т) ,

где

Q =- RH³ -Pr         -R

,Q_C =- RH 3

cc

R = R i

, Q d

R = R i

= A d H * ( P H , P d )

– функции массового расхода газа на входе в зазоры соответствующих областей и на выходе из кольцевых диафрагм, где Ad – критерий подобия питающих отверстий, Ψ – функция истечения Прандтля [2].

Уравнение силового равновесия вала 1 представляли в виде

W(t) - F (t) = F (t),(6)

где F - внешняя сила, W = Wr + Wc - несущая способность подпятника, d2H(τ) d2τ

W r (t) = ² f ^R ( P r - 1 ) dR , W c (t) = ² f ^R ( P c - 1 ) ^dR , F n (t) = M

R1

- составляющие несущей способности по областям зазора и сила инерции вала 1, M - его масса.

Смещение ε(τ) центра 5 и функцию зазора Hc (τ) находили по формулам

W h = R 2 ( P h - 1 ) ,8 = K m ( W h - W_c ) , H c = H - 8, (8)

где K – податливость упругого кольца 4.

m

Исследование динамики подпятника проводилось для малых колебаний вала 1 в окрестности упомянутой «расчетной точки» при помощи специализированной компьютерной среды моделирования, расчета и исследования газостатических опор (среды СИГО) [4] методами теории линейных динамических систем [6, 7]. Решение краевых задач (1), (2) для линеаризованных и преобразованных по Лапласу уравнений Рейнольдса получено численным методом [5], гарантирующим заданную точность расчета комплексных коэффициентов при интегро дифференциальных изображениях обобщенных координат динамической модели (1) – (8).

Для количественной оценки устойчивости и быстродействия ГП как динамической системы использовали степень устойчивости п [6]. Запас устойчивости ГП оценивали при помощи показателя колебательности П [7] амплитудно-частотной характеристики передаточной функции динамической податливости подпятника K ( 5 ) = A H ( 5 )/ A F ( 5 ) , где A H , A F - лапласовы трансформанты малых отклонений соответствующих функций от их стационарных значений, s – переменная преобразования Лапласа [6, 7].

В качестве входных использовали параметры: давление наддува P h , радиус R 1 , «число сдавливания» о и параметры «расчетной точки» е₀ - статическое смещение центра 5 и нормированный коэффициент настройки сопротивления диафрагм х = ( P 2 — 1 ) / ( P H — 1 ) ^е [0,1], где Pd ₀ -статическое давление смазки на выходе кольцевых диафрагм при статическом зазоре толщины Н ⁰ .

Масштаб 1 ₀ определяли из условия

M = mho/nг Pat 0 = 1, где m – масса вала.

Давление Pd ₀, критерий Ad и податливость Km в режиме «расчетной точки», для которой задачи (1) – (2) имеют аналитическое решение, определяли по формулам

P = 1 + / х Pp2 -1) A =----1 Pd0---- K =-----^°----- d0     (H H   )’ d  Y(Ph,Pdo)lnR1’ m   R0(Ph -Pdo)'

Результаты исследования

На рис. 2 представлены зависимости статической податливости K 0 подпятника от коэффициента настройки χ при различных значениях давления наддува P_H . Поскольку параметры ε 0 и σ не влияют на статические характеристики подпятника, то интерес представляют значения коэффициента χ , при которых подпятник имеет наименьшую статическую податливость. Функция K 0 ( χ ) является унимодальной и, следовательно, имеет единственный минимум, который, как видно из графиков, соответствует χ ≈ 0,45. Расчет динамических характеристик проведен для этого значения χ .

На рис. 3 показано влияние величины статического смещения ε₀ центра 5, что эквивалентно влиянию податливости Km кольца 4, на характер кривых переходного процесса Δ H (τ) при входном силовом воздействии Δ F (τ) в виде δ-функции Дирака [7]. При жестком диске, когда ε 0 = 0 и Km = 0, переходная кривая характеризуется выраженной колебательностью. С увеличением ε 0 и Km колебательность переходных кривых снижается, что выражается в уменьшении амплитуды колебаний. Уже при ε 0 ≥ 0,3, когда в статическом состоянии толщина зазора в центральной области за счет смещения центра 5 уменьшается не менее чем на 30 % и способствует тем самым заметному уменьшению объема смазки в газовом слое, переходная характеристика становится апериодической. При этом для таких режимов сокращается и длительность переходных процессов.

Более полное представление о длительности переходных характеристик дают кривые рис. 4, на которых показано влияние смещения ε 0 на быстродействие подпятника. На графиках видно, что с увеличением ε₀ степень устойчивости η быстро увеличивается, достигает своего максимума и затем уменьшается, что свидетельствует об экстремальном

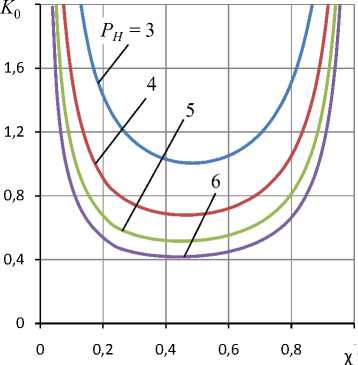
Рис. 2. Кривые зависимости статической податливости K 0 подпятника от коэффициента настройки χ для различных значений давления наддува P H при R 1 = 0,7

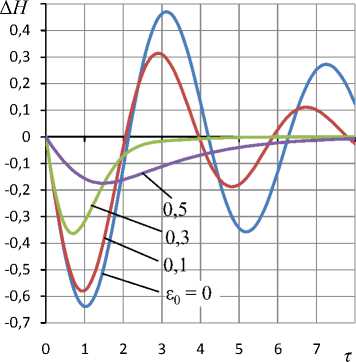
Рис. 3. Кривые Δ H переходного процесса для различных смещений ε 0 центра 5 при P H = 5; χ = 0,45; R 1 = 0,7; σ = 20

Fig. 2. Curves of static compliance of the thrust bearing K 0 as a function of the setting factor χ for different values of supply pressure P_H at R ₁ = 0.7

Fig. 3. Curves Δ H of the transition process for different displacements ε 0 of center 5 at P H = 5; χ = 0.45; R 1 = 0.7; σ = 20

характере зависимости η(ε₀). Установлено, что значениям σ, которые находятся слева от этого максимума, соответствуют колебательные режимы переходных процессов, а справа – апериодические, что подтверждается графиками, приведенными на рис. 3. Анализ приведенных на рис. 4 кривых указывают на то, что функция η(σ), а следовательно, и функция η(ε₀, σ) имеют экстремальный характер и обладают единственным экстремумом-максимумом. Им определяется оптимальный режим быстродействия подпятника. В результате оптимизации функции η(ε₀, σ) установлено, что максимальное быстродействие подпятник имеет при ε 0 = 0,31 и σ = 13, что соответствует экстремуму η(ε 0 , σ) = 1,52. Аналогичный подпятник с жестким кольцом 4 (ε₀ = 0) имел бы наибольшее значение η = 0,13. Отсюда следует, что примененное в подпятнике усовершенствование при оптимальном выборе параметров, влияющих лишь на динамику конструкции, позволяет более чем на порядок повысить ее быстродействие.

На рис. 5 изображены зависимости показателя колебательности П от «числа сдавливания» σ для различных смещений ε 0 . Подпятнику с жестким кольцом 4 (ε 0 = 0) соответствует кривая, на которой П > 5, что характеризует подпятник как резонансную систему слишком высокой колебательности.

С увеличением ε0 показатель Π уменьшается, и уже при ε0 ≥ 0,2 подпятник приобретает свойства хорошо демпфированной динамической системы, для которой показатель П не должен превосходить значений 1,1 – 1,5 [7]. Как видно из графиков, при ε0 ≥ 0,3 зависимости Π(σ) безрезонансны (П = 1), подпятник становится неколебательной динамической системой с апериодическим характером переходных процессов, обеспечивая конструкции наибольший запас устойчивости.

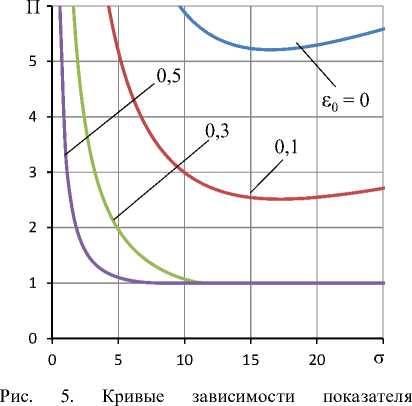
колебательности Π от «числа сдавливания» σ для различных смещений ε0 подвижного центра при PH = 5; χ = 0,45; R1 = 0,7

Fig. 5. Curves of the oscillation index Π at the “number of compression” σ for different displacements ε₀ of the moving center for P H = 5; χ = 0.45; R 1 = 0.7

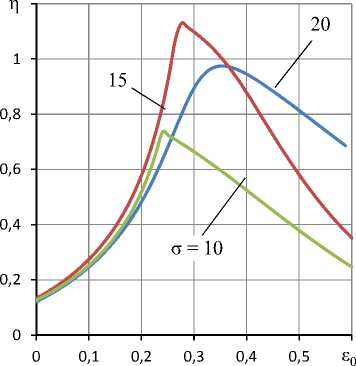
Рис. 4. Кривые зависимости степени устойчивости η от смещения ε₀ подвижного центра для различных значений «числа сдавливания» σ при P_H = 5; χ = 0,45; R 1 = 0,7

Fig. 4. Curves of the degree of stability η from the displacement ε₀ of the moving center at different values of the “compression number” σ for P H = 5; χ = 0.45; R ₁ = 0.7

В заключение приведем пример расчета оптимальных по качеству динамики размерных величин и характеристик подпятника радиусом r 0 = 0,07 м с валом массой 12 кг при PH = 5; R ₁ = 0,7; χ = 0,45; ε₀ = 0,31, σ = 13, для которых η = 1,52 и статическая несущая способность W 0 = 1,86.

Используя (3) и (9), найдем формулу для определения размерной толщины смазочного слоя в «расчетной точке»:

144πμ² r

.

h 0 = Г о5 --------;

mp_a σ²

Принимая μ = 18 ^• 10^-6 Па ^• с и pa = 106 кПа, получим h 0 = 38 мкм. В этом режиме подпятник имеет несущую способность w ₀ = ^п r o² pW = 2,9 кН.

Преобразовав (9), определим величину масштаба текущего времени:

mh t0 = —j-°- = 0,54мс. πr02pa

Используя известную зависимость [7], вычислим время затухания переходного процесса пп 0 η , .

Полученные результаты свидетельствуют о том, что применение опорного центра на упругом подвесе позволяет полностью устранить характерные для кругового подпятника с кольцевыми диафрагмами недостатки качества его динамики и превратить конструкцию в динамическую систему с оптимальными динамическими характеристиками – высокими показателями степени устойчивости, апериодическим характером переходных процессов, величинами показателя колебательности, которые характерны для идеально демпированных динамических систем.