Качество обращения волнового фронта квазивырожденным четырёхволновым преобразователем излучения на тепловой нелинейности

Самарский государственный университет

Получен вид функции размытия точки квазивырожденного четырёхволнового преобразователя излучения на тепловой нелинейности. Проанализированы зависимости ширины модуля функции размытия точки в плоскости оптимальной фокусировки от отношения волновых чисел волн накачки и толщины нелинейного слоя для схем с попутной и встречной геометрией.

Интерес к квазивырожденному четырехволновому взаимодействию т 1 + m 2 - т 1 = m 2 обусловлен возможностью наряду с получением волны с обращенным волновым фронтом одновременно осуществлять перевод излучения с одной частоты на другую, что оказывается предпочтительно при решении целого ряда задач [1-3]. Если качество обращения волнового фронта вырожденным четырехволновым преобразователем излучения на тепловой нелинейности изучено достаточно подробно [4-7], то вопрос о качестве обращения волнового фронта квазивырожден-ным четырехволновым преобразователем излучения остается открытым [8]. Одним из наиболее распространенных методов исследования соответствия комплексных амплитуд сигнальной и объектной волн при четырехволновом взаимодействии является метод функции размытия точки [9].

Пусть в среде с тепловой нелинейностью распространяются две волны накачки с комплексными амплитудами A ₁ и A ₂ и частотами ω ₁ и ω ₂ и сигнальная волна с амплитудой A ₃ и частотой ω ₁ . В результате четыре х волнового взаимодействия генерируется объектная волна с комплексной амплитудой A ₄ и частотой ω ₂ .

Стационарное волновое уравнение, описывающее такое взаимодействие, есть

{ ^{v 2 +} [ ^k j I ^{1 +} t- ds^8T '

V n 0 j u±)

—

( 4          / X )(1)

- 2 ik j a j ]} I £ A j exp ( imt ) + к .с. I = 0.

V j=1                   7

Здесь n0 j – среднее значение показате-ωn ля преломления, k. = ——j - волновое число, c aj - коэффициент поглощения, k 1 = k3, k2 = k4, a1 = a3,a2 = a4, gT- изменение температуры, обусловленное выделением тепла при поглощении излучения.

Уравнение (1) необходимо дополнить уравнением Пуассона

V25T +     {a (A + A3VA* + A* 1 +

Л CpV      ^{1        1} i

+ a ₂ ( A 2 + A ₄ ) ( A *+ A ₄ * ) } = 0

, (2)

где Л - коэффициент теплопроводности, C p - удельная теплоемкость, v - объемная плотность вещества.

Будем рассматривать четырехволновое взаимодействие волн в среде в приближении заданного поля по волнам накачки, при условии, что коэффициент преобразования мал (| A ₁₂| >> | A 3| >> | A ₄| ). Распределение интенсивности можно представить в виде

I = 1L AA. + Ai A* + A* A3. (3) j1

С учетом сделанных предположений волновое уравнение распадается на четыре уравнения

7           л 2 dn c* rrt

^{{ v} 2 ^{+ k}j V ^{1 +} n ; ; dT ⁵ T o |

2 ik j a j } A j = 0,     j = 1 - 3,

{ V ² + k 4 f l + 2- dn 8T,'

V    n 04 dT )

—

2 ik4a4} A. + 2^ dn 8T31A = 0, n04 dT

A "*

dA ₄ ( κ ₄ , z )     k ₄ k ₄ dn

----X-----+ i -j—{ STO(>JLoVz) -dz       k4z n04 dT

а уравнение Пуассона разбивается на два уравнения

^

- ia4} A4(k4, z) =

i^k4- dn STM(Kr k4zn04 dT

= ^К 4 ^{- К} 2 , z ) X . (13)

V ² ST ₀ +

a1 A1 A* + a2 A 2 A*

V ² ST ₃₁ + О ^{л c} p ^v

,^л c p ^v

(A1 A3* + A* A3

= 0

,

) = 0 . (7)

Здесь δT ₃₁ и δT ₀ быстро и медленно меняющие в пространстве составляющие температуры ( ST = ST 0 + ST 31 ) .

Разложим быстро осциллирующую в пространстве составляющую изменения температуры по гармоническим решеткам

—— — ——

ST ₃₁ ( r ) = J ST ₃₁( k _t , z )exp( - iK T p ) dK _T . (8)

Здесь δT ₃₁ – амплитуда спектра тепловой решетки, p - поперечная составляющая радиус-вектора r , К _T - пространственный вектор гармонической тепловой решетки.

Пусть волны накачки являются плоскими волнами

^A j ⁽ r ) = A j 0 ^{( z} ) exp ^{{ - iK} j ^{p - - ik} jz ^{z }} , (9) j = 1,2 .

Сигнальную и объектную волны разложим по плоским волнам

^Am ⁽ r ) = J ^Am ^{( K} m , z ) ^eXP { — ^{i K} m P ^{- ik}mz z } ^{d K} m , m = 3,4.

Здесь К j и k j _z - поперечная и продольная составляющие волнового вектора k _j .

В приближении медленно меняющихся амплитуд с учетом (9), (10) уравнения (4), (5)

примут вид

dA j 0 dz

, . k, [ kj dn + 'l I --j--™ kjz [n0J —

n 0 j dT

δ T 0

- i a j ^ A j ₀

= ⁰; (11)

j= 1,2,

dA3(i<3, z) dz

+ iT^ {k^ dn STo( z) k3z n03 dT

^

- ia3} A3(k3, z) = 0

;

A 2o ( z )exp { - i ( k 2 - k 4 ) z^z }

Уравнения (11)-(12), (6), (7) необходимо дополнить граничными условиями для амплитуд волны накачки A ₁ и сигнальной волны:

A 10 ( z = 0) = A 1⁰0 ,

A 3 (K 3 , z = 0) = A ,o (i T 3 >.

для температуры:

STo( z = 0) = STo( z = P) =

= ST ₃₁( z = 0) = ST ₃₁( z = P ) = 0^.

Граничные условия для температуры записаны при условии отвода тепла от обеих граней нелинейного слоя.

Решая уравнения (7) с учетом граничных условий и изменения амплитуд волны накачки и сигнальной волны по нелинейному слою (решение уравнений (11), (12)), получим

ST ₃1 ( K t , z ) =

в2 - KzJ 2shKTI

X

{ exp( - K_Tz ) [ exp( K_T P ) - exp( - в P ) ] } +

^{+         {ex} p ^{( K} T ^z ) ^X

2 shKTP

[ exp( - в P ) - exp( - K_T P ) ] -

^- exp ^{( - e} z ) }

Здесь f  ^{[ a} 1 A 10 A 30 ^{( к} 3^{) ]}/^л C _— ^v ,

K j = I К t\ , в = 2 a ₁ + i ( k — ₁ -

. (14)

—► k3)z,

K _T = K ₁ - K ₃ .

Подставив (14) в (13) и проинтегрировав по координате z , найдем с точностью до

постоянного множителя амплитуду пространственного спектра объектной волны.

В схеме со встречными волнами накачки при использовании граничных условий

A J z = €) = A 2o ,

A4(k4, z = €) = 0

амплитуда пространственного спектра объектной волны на передней грани нелинейного слоя есть

AK = К + к T , z = 0) = -y f X ^{e  K} T

_<     1    [exp^{( - e € ) -} exp^{( K} T ^{€ )]} _X

2 shK T I         [ k _t + ip ]

[exp( - K _T € - ip € ) - 1] +

^{1   [ex}P^{( - e € ) -} exP^{( -K} T ^{€ )]} _X

2 shK T €         [ k _t - ip ]

г л л            exp( - в € — ip € ) — 1 )

[ехр(Кт€ - ip€) -1] +  1      / 7— } ,л- в + ip          (15)

где p = ( k 2 - k 4 ) z .

Выражение для амплитуды пространственного спектра объектной волны на задней грани нелинейного слоя в схеме с попутными волнами накачки при использовании граничных ус-~ ловий A2o(z = 0) = A20, A4(к4,z = 0) = 0 полностью совпадает с выражением (15).

В параксиальном приближении

? ? loo

( k 1 - k 3 ) z = —( к 3² - K^X

2 k ₁

p=т^(к 4- K 2)

2 k ₂

в схеме с попутными волнами накачки,

p=-т^(к4 - K2)

2 k ₂

ми волнами накачки.

в схеме со встречны-

Зная амплитуду пространственного спек-т ~ ра объектной волны при условии A 3 ( K ₃ ) = const , найдем функцию размытия точки (ФРТ) четырехволнового преобразователя излучения

■                  ;^ z-        -       -

G ( P, Z 3 , Z 4 ) = J A 4 ( K 4 = K 2 + K t ) X

-^

exp

-i^- n-iKKL, iK<^ ^iK 4 ^P 2 k 1 ^{3 +} 2 k ₂ ^{Z 4}

dκ ₄

Здесь z ₃ – расстояние от плоскости фокусировки сигнальной волны до передней грани нелинейного слоя, z ₄ – расстояние от плоскости фокусировки объектной волны до передней грани нелинейного слоя в схеме со встречными волнами накачки, до задней грани нелинейного слоя в схеме с попутными волнами накачки, ~ ^{n  n  n}   ~ M?

A 4 (K 4   K 2 + K T )   A 4 (K 4 K 2 + K T , Z0)

- в схеме со встречными волнами накачки, ~ (? = ? 4- ? = ~ (? = ? 4- ? 7 = Л

A4 (K 4   K 2 + KT )  A4 (K 4   K 2 + KT , Z€ в схеме с попутными волнами накачки.

Схема со встречными волнами накачки

Пусть волны накачки распространяются навстречу друг другу строго вдоль оси Z.

Численный анализ выражения (16) с учетом (15) показывает, что функция размытия точки зависит от модуля поперечной координаты p =|/ ?| и с ее увеличением модуль ФР Т монотонно уменьшается. Введем понятие ширины модуля ФРТ ( А р ) , характеризующего разрешающую способность четырехволнового преобразователя излучения

G ( P ^{= Р}Т V ² 7

= 2 G ( р = 0) .

При фиксированном положении плоскости фокусировки сигнальной волны существует положение плоскости фокусировки объектной волны, в которой ширина модуля ФРТ минимальна (плоскость оптимальной фокусировки ^{( Z} 4 _Op_t ) ).

На рис. 1 (кривая 1) приведен график зависимостей нормированной ширины модуля ФРТ в плоскости оптимальной фокусировки (Ар' = Ар ■ k 1) от отношения волновых чисел волн накачки. Ширина модуля ФРТ в плоскости оптимальной фокусировки мини- мальна, если отношение волновых чисел волн накачки близко к единице. С увеличе- k2

нием отношения волновых чисел при k > ширина модуля ФРТ, монотонно увеличива- ясь, выходит на постоянное значение, величина которого определяется толщиной нелинейной среды и значением волнового числа первой волны накачки.

При фиксированных параметрах волн

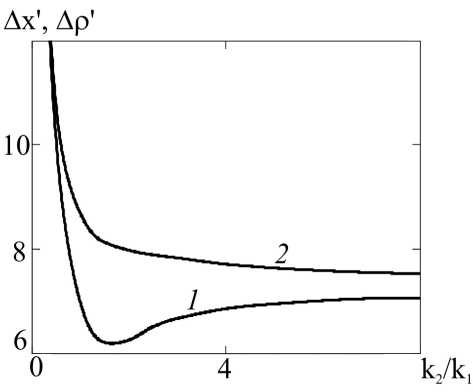
Рис. 1. Зависимость ширины модуля ФРТ от отношения волновых чисел волн накачки в схеме с попутными волнами накачки (кривая 1), в схеме со встречными волнами накачки (кривая 2) при а ^ = 1.6 , к 2 £ = 160

Ax', Ар*

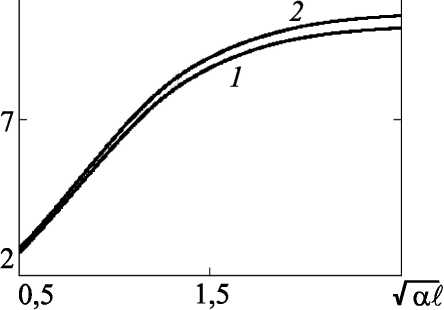
Рис. 2. Зависимость ширины модуля ФРТ от толщины нелинейного слоя в схемах со встречными волнами накачки (кривая 1), с попутными волнами накачки (кривая 2 ) при к 2 [ к^ ~ 17

Ар'

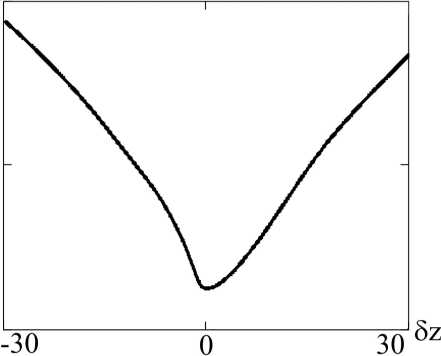
Рис. 3. Зависимость ширины модуля ФРТ от отстройки плоскости фокусировки объектной волны от плоскости оптимальной фокусировки.

накачки увеличение толщины нелинейного слоя приводит к монотонному росту ширины модуля ФРТ (рис. 2. кривая 1). Если нелинейная среда “тонкая” ( а £ <  1 ) , то ширина модуля ФРТ прямо пропорциональна _£ ¹².

По мере отстройки плоскости фокусировки объектной волны от плоскости оптимальной фокусировки ( 5z = z 4 — z 4, opt ) происходит резкое увеличение ширины модуля ФРТ (рис. 3)

Схема с попутными волнами накачки

Пусть при распространении волн накачки выполняется условие К1 + К2 = 0. В этой схеме изменение ФРТ четырехволнового преобразователя излучения зависит как от кор-динаты x , так и от координаты y . Направление координатных осей X и Y выберем таким образом, чтобы ось X лежала в плоскости волновых векторов волн накачки, а ось Y была направлена перпендикулярно этой плоскости. Введем понятие ширины модуля ФРТ в плоскости волн накачки (Ax = |x1 — x2|) и в плоскости, перпендикулярной плоскости волн накачки (Aу = |у 1 — у21), где Х1 2 и У1 2, определяются из условий

|^{G (} x 1,2 , У = ⁰⁾| = 2 ^G max ,      (19)

|^{G (} У 1,2 , x = ⁰⁾| = 2 ^G max .     (20)

Здесь G – максимальное значение мо-max дуля ФРТ.

На рис. 1 (кривая 2) для плоскости перпендикулярной плоскости волн накачки приведен график зависимости нормированной ширины модуля ФРТ в плоскости оптимальной фокусировки (Ax' = Ax • к1) от отношения волновых чисел волн накачки. В плоскости волн накачки значение ширины модуля ФРТ отличается от значения в плоскости перпендикулярной плоскости волн накачки менее чем на 1%. С увеличением отношения волновых чисел нормированная ширина мо- дуля ФРТ в плоскости оптимальной фокусировки монотонно убывая выходит на постоянное значение.

Как и в схеме со встречными волнами накачки увеличение толщины нелинейного слоя приводит к росту ширины модуля ФРТ (рис. 2.кривая 2). При этом зависимости Д х и Д у от толщины нелинейного слоя с точностью 0.1% при к ₂ [к_х ~ 17 совпадают.

В заключение приведем оценки ширины модуля ФРТ квазивырожденного четырехволнового преобразователя излучения на тепловой нелинейности. Пусть тепловая решетка записывается излучением CO ₂ лазера ( Л = 10.6 мкм ) , а считывается излучением He - Ne лазера ( Л 1 = 0.63 мкм ) . В качестве нелинейной среды рассмотрим слой ацетона ( а ₁ = 40 см ^{- 1} , n = n ₂ = 1.33 ) толщиной £ = 400 мкм . Численный анализ выражения ФРТ показывает, что ширина модуля ФРТ в плоскости оптимальной фокусировки в схеме с о встречными волнами накачки равна Д р = 9 мкм , в схеме с попутными волнами накачки - Д х ~ Д у ~ 10 мкм . Отстройка плоскости фокусировки сигнальной волны от плоскости оптимальной фокусировки на 3 мм в схеме со встречными волнами накачки приводит к увеличению ширины модуля ФРТ до 14.5 мкм.

Полученное значение ширины модуля ФРТ определяет придельное (максимальное) значение разрешающей способности квазивы-рожденного четырёхволнового преобразовате- ля на тепловой нелинейности, качественно совпадают с экспериментальными результатами работы [8], в которой для приведённых выше параметров нелинейной среды и взаимодействующих волн наблюдалось восстановление одномерной сетки с диаметром проволоки 35 мкм.