Калибровка системы стереоскопического компьютерного зрения

Предметом исследования является калибровка, стереокамеры в широком смысле. Под калибровкой понимают подбор параметров для минимизации искажений при формировании 2П-изображения трехмерного мира.

В формировании изображения большую роль играет оптическая система, камеры. Она. вносит свои геометрические искажения. Во-первых, это пятна, образуемые из-за. пыли

«Московский физико-технический институт (государственный университет)», 2018

и царапин на стеклянных поверхностях. Во-вторых, это различного рода аберрации, приводящие к нарушению расположения точки изображения в реальной оптической системе по отношению к идеальной. Аберрации частично или полностью устраняются диафрагмированием [10], что, кроме положительного, дает и отрицательный эффект -эффект виньетирования, об устранении которого рассказано в [6], но в нашей статье он рассмотрен не будет. Поэтому существует третий вид искажений - снижение яркости изображения по направлению от оси оптической системы к периферии. Так как данное явление проявляется как отклонение значения выходного сигнала разных элементов матрицы, вызванного одинаковым входным воздействием, и является детерминированным в пространстве и независимым от времени, его можно рассматривать в совокупности с геометрическим шумом матрицы, который мы и будем минимизировать по ходу статьи. О других искажениях подробно рассказано в работе [4], что выходит за рамки нашей статьи.

Развитие технологий расширило возможности автоматической обработки фото- и видеоизображения. Так, например, появилась такая дисциплина, как фотограмметрия. Фотограмметрия применяется для проведения измерений в технике, медицине, промышленной автоматизации, исследованиях окружающей среды и других областях, и более качественная оценка позволит добиться лучших результатов в данных областях. В классическом случае используется линейный (или двухточечный) алгоритм коррекции, рассмотренный в [5]. В нашем же случае используется другой метод с большим количеством контрольных точек, что позволит получить лучшие результаты.

Предполагается найти калибровочную матрицу М, которая будет включать в себе внутренние и внешние параметры камеры. Внешние параметры можно представить как матрицу перехода Т из системы координат объекта в систему координат камеры. Предлагаемый метод позволит находить данную матрицу для любых конфигураций камер.

Для решения поставленной задачи рассматриваются системы координат объекта и камеры в однородных координатах. Однородные координаты обладают тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же ненулевое число. Из-за этого количество координат, необходимое для представления точек, всегда на одну больше, чем размерность пространства, в котором эти координаты используются.

Данный метод находит свое применение при построение карты глубины изображений.

2.    Модель

Перед нами стоит проблема съемки произвольного объекта. Зададим две системы координат: А - для задания положения камеры и В для задания положения объекта. Калибровка камеры состоит из двух составляющих: внешних и внутренних параметров. Внешние - это преобразование Т из реального мира в ЗП-систему координат камеры (рис. 1).

Для начала рассмотрим, как задается положение произвольной точки Р в системе координат А (1). Легко заметить, что для системы координат В положение задается аналогично.

( ^Аж\

^Ау\ _о ОР = (^Ах • І а ) + ( ^а у • j A ) + (^Az • ^).                 (1)

Аг )

Рассмотрим переход из системы координат объекта В в систему координат камеры А рис. 3. Он состоит из смещения и поворота.

Смещение в векторном представлении можно выразить так:

^вР =^А Р ₊^в ( Оа).                               (2)

В однородных координатах [2] выражение (2) можно выразить в виде перемножения матриц:

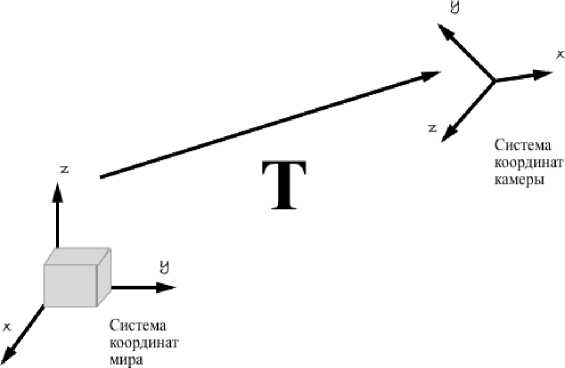
Рис. 1. Преобразование из системы координат объекта, в систему координат камеры

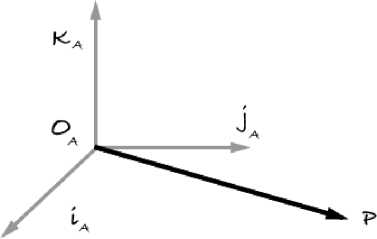
Рис. 2. Положение точки в системе координат

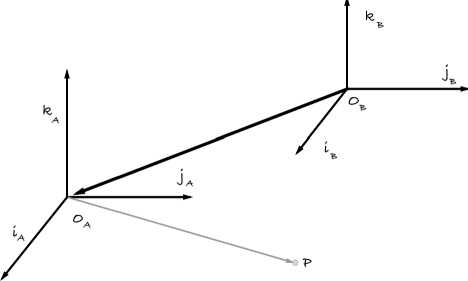
Рис. 3. Переход между системами координат

G ) - ( o '^в О ^Р )•

А поворот системы координат можно описать так же, как и выражение (3):

—

ОР - ( г_А J A   к л)

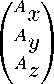
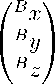
или в матричном выражении ^вР - АА R^AP, где матрица ^вR описывает положение системы координат А в системе координат В. Тогда положение точки Р в системе В можно выразить как (4):

( ІАІВ  ЗАІВ

ІАЗВ  ЗАЗВ гА^в  ЗАкв

кАІв к АЗ в I = (В г а В ЗА  В кА) .

кАкв

Для однородной системы координат

■ ) =     ■   0) = ■ )•

Жесткое тело будет иметь шесть степеней свободы. Мы можем однозначно определить положение тела в пространстве, зафиксировав две его точки [1].

Далее рассмотрим внутренние параметры. Это преобразование из ЗИ-изображения в плоское (рис. 4). Для этого рассмотрим идеальную проекцию изображения. Пусть у нас есть система координат камеры с осями х, у, z и система координат плоского изображения с осями u, v (рис. 4).

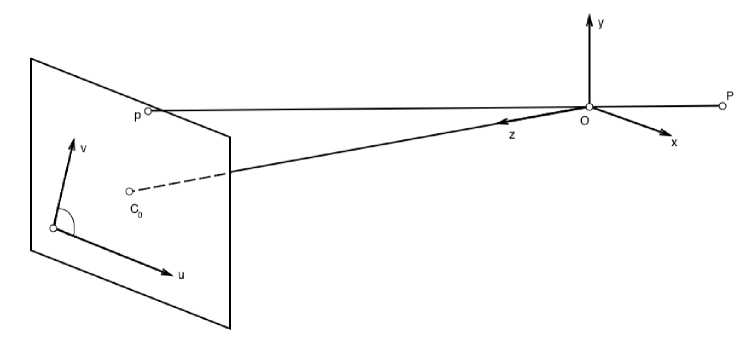
Рис. 4. Преобразование из системы координат камера, в систему координат изображения

Тогда положение точки в координатах п, в можно выразить через координаты ж, у, д с помощью следующего выражения, где / - фокусное расстояние оптической системы камеры:

п = / ^Ж ,

д

в = / ^- .

д

В реальном мире нужно учитывать количество пикселей на. миллиметр. Обозначим масштаб как а. Причем пиксели не всегда квадратные, поэтому введем 3 для второй оси. Мы считаем, что центр проекции у нас находится посередине проекции, в реальных камерах существует смещение вследствие несовершенства производства, и его нужно учитывать. Для этого сведем смещения по каждой из осей как по и во:

п = а—+ по, д в = 3- + во. д

Так же нужно учитывать, что векторы пив могут быть не перпендикулярны. Для этого введем угол отклонения относительно вертикали Ө и новые координаты и’ и v’.

Тогда, соотношения между реальными и идеальными системами координат можно представить как в' sin(Ө) = в, п' = п — сов(Ө)в' = п — еө1(Ө)в.

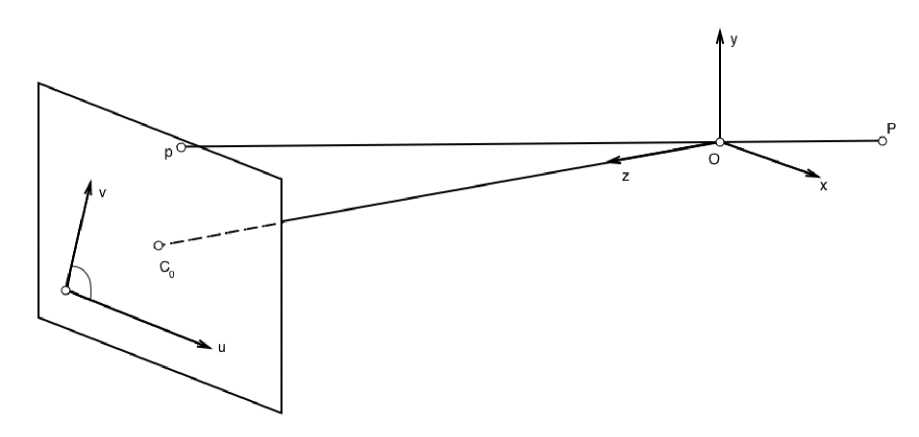
Рис. 5. Скос осей к’ и и’ относителыю кии

Учитывая все представленные ранее замечания, получим следующие уравнения:

к = а— — a cot(0)- + ко, г           г и = ■ L+ уо.

sm( p ) г

Наша модель учитывает два масштаба, два смещения и скос. Переведем эти выражения в однородные координаты, чтобы объект не менялся при умножении координат на одно число. И представим это в виде матричного выражения:

/ г * к\    /a  -a cot(3)  ко  0\

I г *и I = ( 0     Shfc     ио  0 I   -.

\ г /    \0      0       10/

Мы можем представить перевод в новые координаты простым выражением р = Кр. где матрица К есть (5)

( f S с_ж\

0 af су ,(5)

0   01

где f - фокусное расстояние, s - скос, а - масштаб и смещения с _х и С у. Теперь мы можем совместить внешние и внутренние параметры и получить итоговое выражение:

Р’ = К (bar^p, р = Мр.

Представим матрицу М в однородных координатах, где т^х, т^х, т^, т ^

компоненты

матрицы М:

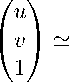
s * к s * и s

Т т 1 т ^т2 т ^т3

/ рж\

Ру Рг где ~ обозначает, что у нас два одинаковых вектора с точностью до умножения всех координат на число:

— m1 • Р и = ----—, m3 • Р

— m2 • Р в = ----—.

m3 • Р

Тогда параметры камеры можно выразить в одно выражение

Мзх4 = КзхзРзх4 Рзх4Тзх4.

Соответствующие матрицы имеют вид

( f s ж_с

0 af ус , 0   01

/1 0 0 0\

Р =  0 10 0 , р_ (^3х3

0зх1     1,

^ 3 х 3

0зх1

Полученное выражение позволяет проецировать объекты на фотопленку с учетом внешних и внутренних параметров камеры.

3.    Калибровка камеры

Основа калибровки заключается в том, что мы знаем положение некоторых точек в трехмерном пространстве и сопоставляем их с изображением. Получая тем самым некоторое преобразование из реального мира в изображение:

W * и

W * в

W

mn m i2 m i3 m i4 \				X^ Y
m 2i	m 22	m 23	m 24	Z
m 3i	m 32	m 33	m 34/	1

Рис. 6. Калибровка камеры по точкам

С помощью теодолита [3] сначала измеряется расстояние до маркеров: (X,Y,Z, 1)^т и мы можем найти и и в. Мы получаем пару выражений для каждой точки:

U j

mooX j + moiY j + mo2Z j + т оз т 2о X j + m2iY j + m22Z j + m 23 ’

т іо Хг + тц Үі + mi2Z i + т із

Vi = ------------------------------ т2оХг + т2і Үі + m22Zi + т2з

.

Выражения (6) и (7) представим в

матричной форме как А хт (8), где т - столбец из

компонент матрицы М:

	/ тоо\
	т іо
	т о2
	т оз
	т іо
(Хг  Y   Zi  1  0   0  0  0   -игХг  -uiYi  -uiZi  -иЛ V 0   0    0  0  Х г   Ү і  Z i  1   -ViХi   -V i Y i   -V i Z i   -V i)	ті2   = ( 0 )-    <8>
	т із
	т 2о
	т 2і
	т 22
\ т2з/

Чтобы решить это уравнение, необходимо минимизировать ||А х т|. Решением будет собственный вектор т* матрицы А^ТА с наименьшим собственным значением. Нам нужно шесть или более точек.

Вариант 1. Как мы знаем, мы можем поделить все элементы матрицы т на число так, чтобы один из элементов был равен 1. Но стоит быть осторожным, когда т2з близко к 0,

в этом случае стоит воспользоваться вторым вариантом:

~

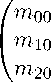
т оі тіі т 2і

т о2

т і2

т 22

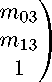
Х»

ү

Z

\ 1/

и тогда.

иг =

т оо Хг + т оі Үг + т^г + т оз т 2о Хг + т 2і Ү + m22Z i + 1

т іо Хг + т_п Ү і + т^г + т із

Vi = ------------------------------ т2оХг + т2іҮг + m22Zi + 1

.

Перемножив и г и V i, которые известны, так как это положение точки на изображении, легко получить т. Этот метод имеет несколько позитивных и негативных сторон. Позитивные: очень легко формулируется и решается. Негативные: явно не отображает параметры камеры и допущенное приближение не учитывает радиальное искажение [7], тяжело вводить ограничения.

Вариант 2. Представим матрицу А как сингулярное разложение UDV^T. D - диагональная матрица, a U и V ортогональны. Буд ем минимизировать ||UDV^T т|. Но ||UDV ^тт| = ||DV^Tm| и ||т|| = ^^Тт|. Таким образом, минимизируя ||DV^Tm| л || V^Тт| = 1. сделаемi замену у = V^Tm. Тогда нужно мшшмпзпровать ||Dy|. D - диагональная матрица с сортированными значению по убыванию. Тогда |Dy| минимально, когда, у = (0 0 ... 0 1)^Т. Мы обо значили у = V ^Тт. следовательно, т = Vy. получается, что т - это последний столбец, матрицы V.

4. Замечание

Данным методам измерения присущи геометрические ошибки, которые нужно минимизировать. Допустим, у нас есть проекция М. Х г - множество точек в 3D-пространстве и на. плоскости, на. которую производится проекция множество точек

идеальной проекции Xi и точки реальной проекции (рис. 7). Сумма расстояний между идеальной и реальной проекциями и будет составлять геометрическую ошибку Е (9):

е = £Д4Д). i

Её мы и будем минимизировать:

min м

^2 d(x'_i,M X i ).

І

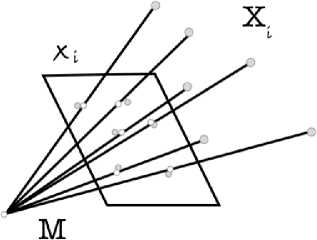
Рис. 7. Геометрическая ошибка при проецировании

Число точек, по которым проводится калибровка, должно быть больше пяти, тогда ошибка (9) будет минимальной. Существует алгоритм минимизации ошибки.

• 1)    Линейное решение:

• • нормализация X_i = U X_i , X_i = Т x_i,

• е минимизация прямого линейного преобразования.

• 2)    Минимизация геометрической ошибки: используя линейную оценку в качестве начальной точки, минимизировать ошибку:

min ^^ d(Xi, MMX i ).

i

• 3)    Денормализация:

5.    Результаты 6.    Вывод

M = Т ^-1 MIU.

В итоге мы получаем матрицу М, содержащую все параметры камеры. И теперь можем найти центр ЗП-камеры из этой матрицы. Представим M как M = [Q|6], где M имеет размерность 3 х 4 іі 6 - это последний столбец матрицы M. Центр ЗП-камеры обозначим С. тогда MC = 0. Докажем это. Допустим, тонка X находится где-то между Р и С:

X = АР + (1 - А)С, тогда проекция будет x = MX = AMP + (1 - A)MC.

Для любой точки Р все точки на PC проецируются на Р, следовательно, MC должно быть равно 0. Полученные результаты позволяют добиться улучшения при построении карты глубины согласно [8] и [9]. Как можно заметить, правое изображение визуально чище левого.

Рис. 8. Карта, глубины без оптимизации и с применением оптимизации

Основным результатом является применимость метода оптимизации параметров для ЗИ-камер. Метод дает видимый результат при построении глубинных карт. Таким образом, абстракция от физических параметров позволяет его применять на любых камерах. Данная оптимизация не требует дополнительного оборудования, что положительно влияет на экономическую составляющую.