Калибровочные симметрии Кэли-Клейна

Теории с неполупростыми калибровочными группами, являющимися симметриями пространства-времени, используются в гравитации и механике сплошных сред достаточно давно [1]. Калибровочная теория гравитации основывается на группе Пуанкаре, являющейся полупрямым произведением группы Лоренца SO(3,1) и пространственно-временных трансляций T(4) [2]. В механике сплошных сред калибровочными полями описываются дислокации, дисклинации, точечные дефекты [3]. В качестве калибровочных групп используются группы афинных преобразований GL(3) XT(3), а также полу-прямое произведение группы вращений SO(3) и группы трансляций T(3), SO(3) (XT(3). В физике частиц нам известно лишь одно направление, где изучаются возможности неполупростых симметрий [4]. Важную роль в конформной теории поля и теории струн играет модель Наппи-Виттена, использующая центрально расширенную группу Пуанкаре [5]. В работе [6] изучаются полевые теории Черна-Саймонса с неполупростыми калибровочными группами симметрии. Особенности калибровочных полей с неполу-простой группой симметрии, а также способы построения их лагранжианов изучались в статьях [7]– [9]. В работе [10] калибровочные модели с неполупросты-ми группами, в том числе и с группами Кэли-Клейна SO(3, j), рассматривались с использованием нильпотентных образующих. Предлагаемый подход к описанию неполупростых калибровочных моделей существенно опирается на выбор сферических координат и позволяет обеспечивать массивность калибровочным полям посредством изменения метрики в изопространстве, что оказалось эквивалентно добавлению еще одного инварианта. Идея использовать сферическую геометрию в пространстве полей материи для формулировки бозонного сектора электросла-бой модели воплощена в работах [11]. Здесь же показано, что это позволяет обойтись без хиггсовско-го бозона. Важные аспекты калибровочных теорий в сферических координатах и интерпретация хиггсова поля как конформного пространственного-временно-го метрического фактора обсуждались в [12].

Цель данной работы – построение калибровочной теории с неполупростой группой симметрии. Известно, что предельные переходы или контракции [13, 14] позволяют связывать простые группы и алгебры Ли с неполупростыми. Поэтому представляется естественным использовать контракции для получения и изучения теорий с симметриями непо-лупростых групп. Ранее, в работе [15], мы предложили систематический метод контракции лагранжианов с калибровочной симметрией. Были получены теории с галилеевой и евклидовой калибровочными группами. Их неожиданным и привлекательным свойством оказалась массивность некоторых компонент калибровочных полей. В данной работе мы рассмотрим контракции векторной SO (3) модели Джорджи-Глэшоу (ДГ). Эта модель, в свое время, предлагалась как вариант описания электрослабого взаимодействия. Кроме того, она интересна тем, что обладает монопольными решениями. Мы рассмотрим модификацию ДГ-модели, обобщив метрику внутреннего изопространства. Записав ее в деформированных специальными параметрами ε 1 , ε 2 сферических координатах и полагая квадраты этих параметров равными 0 , ± 1 , получим теории с калибровочными группами Кэли-Клейна. Эти группы действуют транзитивно на соответствующих внутренних двумерных пространствах постоянной кривизны. В радиальных переменных угловые поля можно интерпретировать как координаты на этих пространствах. Далее мы рассмотрим теорему Голдстоуна и механизм Хиггса для изучаемой модели, а также построение лагранжианов для калибровочных полей Кэли-Клейна.

2.    Модель Джорджи-Глэшоу в сферических координатах

Модель ДГ возникает из глобально SO (3) симметричного лагранжиана

L о = ^д Э цФ, Э цф^ - V (( Ф,Ф )) =

=(э^Ф 1)2 +(э^ф2)2 +(э^фз)2 — V(ф2 + ф2 + ф3), (1) инвариантного при преобразованиях ф —> G$ = exp(aiT)ф,           (2)

где Ф = ( Ф 1 , Ф 2 , Ф з ) , T i - генераторы инфинитезимальных поворотов группы вращений G = SO (3)

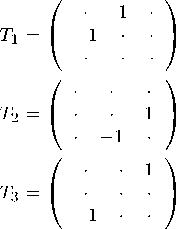
удовлетворяющие коммутационным соотношениям

[Ti ,T j^ = E ijk T k .                   (4)

Здесь ϵ _i j _k абсолютно антисимметричный единичный тензор.

Преобразования (2) во внутреннем изопространстве R ³ с параметрами a i , зависящими от точки пространства-времени x µ , называются локальными. Требование инвариантности относительно локальных или калибровочных преобразований является основным принципом современной теории взаимодействия элементарных частиц [16]– [18]

Ф —> G ( Х ц ) Ф = exp ( a i ( Х ц ) T i ) ф. (5)

Для инвариантности лагранжиана (1) относительно локальных преобразований необходимо изменить производную

9 ц —> D ц = 9 ц ^{+ А} ц , (6)

где калибровочные векторные поля A µ лежат в алгебре Ли so (3) , А ц = A^ i . Из полей А Ц и их производных ∂ µ A ⁱ _ν можно построить лагранжиан калибровочных полей L _YM (для нашей модели мы строим его в секции 8, см. также [16]– [18]) и добавить его к исходному

L = ( D ц Ф, D ц ф ) - V ( ( Ф, ф ) ) + L ym = ( D ц ф ) 2 + ⁺ ( D ц ф ) 2 ⁺ ( ^Ф ) з ^- V ^{( Ф} 1 ^{+ Ф} 2 ^{+ Ф} з ) ⁺ L YM . (7)

Формула D µ ϕ^⃗ _i обозначает i -ю компоненту вектора D µ ϕ^⃗ , а ее квадрат понимается как суммирование по пространственно-временным индексам µ

(М i = ( D 0 ^Ф ) i - ( D ¹ ^ i - ( D 2 ^Ф ) i - ( D 3 ^Ф ) i .

Закон преобразования калибровочных полей A µ при локальных преобразованиях полей материи ϕ (5)

А Ц = GA ц G ” ¹ + G9 ц G ^{- 1} .          (8)

Нам понадобятся выражения (1),(7) в сферических координата х. Предста вим вектор ϕ в виде рп ( б,ф ) , где р = ^ Ф 1 + Ф 2 + Ф 3 есть радиус сферы, а единичный вектор п ( 6,ф ) на поверхности сферы может быть записан в терминах вращений П е SO (3) следующим образом: п ( 6,ф ) = П е i , где e i = (1 , 0 , 0) . Тогда

9 ц ф = П ( 9 ц р + р П ¹ 9 ц п ) е 1 = П( 9 ц р + рЬ ц ) е 1 , (9) где

/ •     ь ц    ь ц \

Ь ц = П ^{- 1} 9 ц П= -b ц    •   ь ц (10)

• -b ³ _µ -b _µ    ·

лежит в алгебре Ли so (3) .

В координатах ρ, b ⁱ _µ лагранжиан (1) выглядит так

L о = ( ^д ц Ф,9 ц ^Ф) ^- V (⁽ Ф,Ф )) =

= (П ( д ц р + рЬ ц ) е 1 , П ( 9 ц р + рЬ ц ) е 1 ) - V ( р ² ) =

= ^{(( д} ц р ⁺ р^Ь ц ) е 1 , ⁽ 9 ц р ⁺ р^Ь ц ) е 1 ) - V ⁽ р ² ) =

= ( д ц р )²+ р 2 ( ( Ь ц ) 2 + ( Ь 3 ц ) 2 ) - V ( р ² ) , (11)

причем ρ и b µ не меняются при глобальных вращениях (2). При локализации лагранжиана (11), учитывая (6), получаем

d ф 1 , ф 2 + d ф 2 , ф з + d ф з ) и их векторном произведении, который, как нетрудно убедиться, также является инвариантом относительно действия группы SO (3)

⃗

⃗

д _ц ф ^ D _ц ф — о

( ^д ц Р + р ° ^{1 ( д} ц + A ^ )° ) e 1 —

— О d d pp + р О ¹ D ^ о) e 1 — О( д ц р + рВ ц ) e 1 ,

d V —

где

В д — О

¹ д _ц О + О

¹ А _ц О — О

¹ И . О .

После вычислений, аналогичных (11), лагранжиан переходит в

L = ^{( д} ц р ) 2 ⁺ Р 2

(B^ + ( b^)²"

^- V ⁽ р ^{2 )+} L YM ⁽¹⁴⁾

и является записью формулы (7) в радиальных переменных. Заметим, что в случае перехода к переменным, часть из которых не меняется при действии группы G ( х _ц ) (в нашем случае это р ), введение компенсирующих полей A µ для удлинения производной (6) при действии на эти переменные не требуется, т.е. D ^ p — д ^ р . Поля В _ц остаются инвариантными В ц — В _ц , поскольку они состоят из калибровочных полей A µ , преобразующихся по закону (8) и полей материи О( 6,ф ) , принимающих значение в группе SO (3) и преобразующихся как О ‘ — G О . Преобразования калибровочных полей и полей материи компенсируют друг друга. Выражение (13) использовалось в [19] в контексте получения массивных теорий Янга-Миллса при нелинейной реализации калибровочной группы.

Мы обобщаем (11) с помощью функции F ( р ) с сохранением глобальной вращательной симметрии и будем рассматривать лагранжиан

L — ( д ^ р ) ² + F ( р ) р ² [ ( b 1 ) ² + ( b * ) ² ] - V ( р ² ) .    (15)

В декартовых координатах это обобщение выглядит как добавление к (1) нового слагаемого

L — ( д ^ ф 1 ) 2 + ( д ^ ф 2 ) 2 + ( д ^ ф з ) ² -

^- V ^{( ф} 1 ^{+ ф} 2 ^{+ ф} з ) ^{+ (} F ^- 1) [ ^{( ф} 2 ^д ц ^ф 1 ^{- ф} 1 ^д ^ ^ф 2 ) 2 ⁺

+ ( ф 2 д ц ф з - ф з д ц ф 2 ) ² + ( ф з д ц ф 1 - ф 1 д ц ф з ) ² ] —

— L 0 + f ( р ) L _a . (16)

Функции F ( р ) и F ( р ) связаны равенством ( F- 1) р ^{- 2} — F - 1 . Интересно отметить, что выражение в квадратных скобках пропорционально лагранжиану нелинейной σ –модели [16]– [17]

L _a — ( д ^ ^ф,д ^ ^ф ) ,       ( ^ф,^ф ) — 1 .      (17)

То же выражение можно интерпретировать и как инвариант, связанный с углом d а , между векторами ( ф 1 , ф 2 , ф з ) и ( ф 1 + d ф 1 , ф 2 + d ф 2 , ф з + d ф з ) :

d а ² — [( ф 1 d ф 2 - ф 2 d ф 1 ) ² + ( ф 2 d ф з - ф з d ф 2 ) ² +

^{+ ( ф} з ^{d ф} 1 ^{- ф} 1 d ^ф з ^{) 2} ] [ ^ф 1 ^{+ ф} 2 ^{+ ф} з ] . ⁽¹⁸⁾

Еще одна возможная интерпретация связана с объемом, построенным на векторах ( ф 1 , ф ₂ , ф _з ) , ( ф 1 +

ϕ 1 ϕ 2

ϕ 3

ф 1 + dф 1 ф2dфз - фзdф2 ф 2 + d ф 2 ф з d ф 1 - ф 1d ф з фз + dфз  ф 1 dф2 - ф2dф 1

Таким образом, лагранжиан (16) есть сумма двух инвариантов, один из которых связан с квадратом длины (1), а второй – с углом (18) или объемом (19). Несколько инвариантов использовал в своих работах при построении многомерных теорий поля в полуримановых пространствах Р.И.Пименов [20]– [22]. Аналогичное обобщение локальных лагранжианов (7),(14) имеет вид в радиальных координатах

L — ( д ц р ) ² + F ( р ) р ² [( В ^ ) ² + ( В ^ ) ²j + L ym , (20)

и в декартовых координатах

L ^— ( D ^ $ ) 1 ⁺ ( D ^ $ ) 2 ⁺ ( D ^ $ ) з ^- V ^{( ф} 1 ^{+ ф} 2 ^{+ ф} з ⁾⁺

^{+ (} F^- 1) ^{ф ф} 2 ^{( D}^4> ) 1 ^{- ф} 1 ^{( D}^4> ) 2j ^{+ ф} 2 2 ^{( D}^4> ) з ^-

ф з ( D ^ $)2^+ ( ф з ( D ^ $ ) 1 - ф 1 ( D ц ^ф) з ) ² . (21)

Уже в (20) видно, что выбор F ( р ) р ² — M ² + f ( р ) дает массивные члены калибровочных полей. Введение дополнительной функции F ( р ) в случае SO (3) выглядит избыточным, но для нашей цели получения лагранжианов с симметриями SO (3 ,е 1 ,е ₂ ) эта функция необходима.

3. Группы Кэли-Клейна и контракции

Напомним кратко, как можно описать все двумерные пространства Кэли-Клейна и их группы движения с помощью контракций группы SO(3) в трехмерном, фундаментальном представлении. Двумерными пространствами Кэли-Клейна мы будем называть поверхности, задаваемые уравнениями x2 + е 1 у2 + е 1 е 2 z2 — const, (22)

где параметры е 1, е2 принимают значения 0, ± 1. Группами Кэли-Клейна называются группы изометрий этих пространств, сохраняющие соответствующую метрику d S 2 — dx 2 + е 1d у2 + е 1 е 2d z2. (23)

Контракция – это сингулярная операция над группой или алгеброй Ли, приводящая к изменению закона умножения в группе и обнулению части структурных констант в соответствующей алгебре [23]. В нашем случае это соответствует значению параметров е к — 0 . При е к — - 1 , т.е. е _к — i , будем иметь аналитическое продолжение.

Один из методов описания возможных контракций и аналитических продолжений группы SO (3) состоит во введении параметров ε ² ₁ , ε ² ₂ в групповую

матрицу следующим специальным способом [14]

G ( e 1 ,e 2 ) = exp ( a i T i ( e 1 ,e 2 )) =

( 2       2 2    \

•     e i a 1 e i e 2 a 3 \

-a 1      •      e 2 a ₂      . (24)

-a 3 -a 2       •    /

Возникающие при этом группы оказываются группами Кэли-Клейна SO (3 , e 1 , e ₂ ) c соотношениями ортогональности, деформированными параметрами ( e 1 ,e 2 )

G * ( e 1 ,e 2 ) I ( e 1 ,e 2 ) G ( e 1 ,e 2 ) = I ( e 1 ,e 2 ) , (25)

сохраняющими следующую квадратичную форму

P 2 ( e 1 ,e 2 ) = ф 1 + e 1 ф 2 + e 1 e 2 ф 3 = ^ ,I ( e 1 ,e 2)^ . (26)

Здесь

I ( e 1 ,e 2 )

•

•

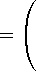
22 ε ₁ ε ₂

Генераторы групп Кэли-Клейна T i ( e ₁ , e ₂ ) имеют вид

• 4.    Глобальные SO (3 ,e 1 ,e 2 ) модели

Рассмотрим сначала контракции и аналитические продолжения в глобальном случае, а затем займемся их локализацией. Чтобы сконструировать лагранжианы, глобально инвариантные относительно преобразований из группы Кэли-Клейна SO (3 ,e 1 ,e 2 ) , перейдем от переменных ф _i и их производных д ц ф _i к переменным p ( e ₁ ,e ₂ ) и Ь ц ( e ₁ ,e ₂ ) по формулам (32). Подставив эти замены в (1), получаем

L = ( д ц p ( e 1 ,e ₂ )) ² - V ( p ( e 1 ,e 2 ))+

+ p ² ( e 1 ,e 2 ) e 1 [ e 2 ( Ь ц ) 2 + ( Ь ц ) 2 ] . (33)

Нетрудно непосредственной проверкой убедиться, что [ e 2 ( Ь ц ) 2 + ( Ь ц ) 2| является инвариантом на орбитах действия группы SO (3 ,e ₁ ,e ₂ ) . Очевидно, что p ( e ₁ ,e ₂ ) и ( д ц p ( e ₁ ,e ₂ )) ² также являются инвариантами относительно действия этой группы. Тогда можно сконструировать следующий SO (3 , e 1 , e 2 ) инвариантный лагранжиан

T 1 ( e 1 ) =     - 1

L = ( д ц p ( e 1 ,e 2 )) ² + e 1 p ² ( e 1 ,e 2 )

^e 2 ( ^Ь ц ) ⁺ ( ^Ь ц ) ⁺

T 2 ( e 2 ) = I •     •

• - 1

•

•

- 1

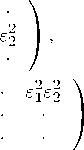
и удовлетворяют коммутационным соотношениям

^[ T 1 ^{( e} 1 ) ^,T 2 ^{( e} 2 ^)] = T 3 ^{( e} 1 ^,e 2 ) , [ T 2 ( e 2 ) ,T 3 ( e 1 ,e 2 )] = e 2 T 1 ( e 1 ) ,

[ T 3 ( e 1 ,e 2 ) ,T 1 ( e 1 )] = e 1 T 2 ( e 2 ) ,           (29)

или

[ T i ^{( e} 1 ^,e 2 ) ^,T j ^{( e} 1 ^,e 2 ) ] = E ijk ^{( e} 1 ^,e 2 ) T k ^{( e} 1 ^,e 2 ) , ⁽³ 0) ^{где E} 123 = ^-€ 213 = 1 , ^€ 312 = ^-€ 132 = ^e 1 , € 231 = ^—E 321 = ε ² ₂ , а остальные равны нулю.

В алгебре Ли, где принимает значение векторное поле b µ , параметры вводятся аналогично

Ь ц ( e 1 ,e 2 ) = fi ¹ ( e 1 ,e 2 ) д ц fi( e 1 ,e 2 ) =

• b1µ

³ b _µ

ε ² 1 b ¹ µ

b ² µ

ε ² 1 ε ² 2 b ³ µ _ε 2 _{2 b} 2 _µ

•

Поля ϕi и их производные ∂µϕi выражаются через поля p(e 1 ,e2) и Ьц(e 1 ,e2) следующим образом ф = p (e 1 ,e2)fi( e 1 ,e2)e1, дцф = fi(e 1 ,e2) (дцp(e 1 ,e2) + p(e 1 ,e2)Ьц(e 1 ,e2)) e1. (32)

Поля p ( e 1 ,e 2 ) и Ь ц ( e 1 ,e 2 ) не изменяются под действием группы Кэли-Клейна, что является очень удобным при анализе контракций.

⁺ ( F ^{( p ( e} 1 ^,e 2 )) ^— 1 ) ^{p 2 ( e} 1 ^,e 2 ) ^e 2 ( ^Ь ц ) ⁺ ( ^Ь ц )

- V ( p ( e 1 ,e 2 )) . (34)

Этот же лагранжиан в декартовых координатах

L = ( д ц ф 1 ) ² + ( e 1 д ц ф 2 ) ² + ( e 1 e 2 д ц ф 3 ) ² -

- V ( ф 1 + e 1 ф 2 + e 1 e 2 ф 3 ) + ^[ F ( ф 1 + e 1 ф 2 + e 1 e 2 ф 3 ) - 1 ] x x [( ф 2 д ц ф 1 - ф 1 д ц ф 2 ) ² + e 1 e 2 ( ф 2 д ц ф 3 - ф 3 д ц ф 2 ) ² +

+ e 2 ( ф 3 д ц ф 1 - ф 1 д ц ф 3 ) ² ] . (35)

Лагранжианы (34)–(35) описывают набор моделей с глобальной инвариантностью относительно групп Кэли-Клейна.

5. Теорема Голдстоуна

В реалистичных моделях потенциал V ( ф ) , инвариантный относительно глобальных преобразований симметрии группы G , выбирается специальным способом для обеспечения ненулевых вакуумных конфигураций поля. При этом группа симметрии вакуумных конфигураций H является подгруппой группы G . В этом случае выполняется теорема Голдстоуна, которая гарантирует появление безмассовых частиц при спонтанном нарушении симметрии G ^ H при выборе конкретного вакуума [16]– [17]. Покажем, что в случае SO (3 , e ₁ , e ₂ ) симметрии появляется одно массивное поле и два безмассовых. Выберем в (35) потенциал V в виде

V = | ⁽ ф 1 + e 1 ф 2 + e 1 e 2 ф 3 - ^ ) .    (36)

Потенциал (36) имеет минимум при ф 1 + e 1 ф 2 + e 1 e 2 ф 3 = ^m=.          (37)

Таким образом, множество всех возможных вакуумных состояний – это поверхности Кэли-Клейна (37). В качестве вакуума выберем и в декартовых

L ^{— ( D} ц ^ф ) 1 ^{+ ( е} 1 ^D ц ^ф ) 2 ^{+ ( е} 1 ^е 2 ^D ц ^ф ) 3 ^—

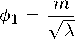
Ф 2 = Ф 3 = 0 •

Возмущения вблизи этого вакуума обозначим через

- V(Ф1 + е 1 ф2 + е 1 е2фф3) + [f(ф 11 + е 1 ф2 + е 1 е2ф2) - 1]х х  фф2(Dцф)1 - ф 1(Dцф)2j +

m

^Ф 1 ^— \ л ^{+ а}’

Ф 2 = и 2 ,

Ф 3 = и 3 •

^{+ е} 1 ^е 2 ( ^ф 2 ^{( D} ц< ^ф ) 3 ^{- ф} 3 ^{( D} ц ^ф ) з ) ⁺

Подставляя (38) в (36) и оставляя только слагаемые не выше второго порядка, имеем потенциал

^{+ е 2} ( ^ф 3 ^{( D} ц ^ф ) 1 ^{- ф} 1 ^{( D} ц ^ф ) 3 )

⁺ L YM ^{( е} 1 ’^е 2 ) •

V — 2 m ² а ² .

Лагранжиан (35) становится таким

L — ( д ^ а ) ² + ( е 1 д ц и 2 ) 2 + ( е 1 е 2 д ^ и з ) ² - 2 m ² а 2 +

+ mf ( ( д ^ и 2 ) 2 + е 2 ( д ц и з ) ² ) , (40)

где через f 0 мы обозначили первый не зависящий от полей член в разложении функции F- 1 . Поле а приобретает массу, тогда как поля u 2 , u 3 остаются без-массовыми, но их кинетические слагаемые испытывают конечную «перенормировку». При разных значениях ε 1 , ε 2 вакуумный вектор инвариантен относительно подгруппы SO (2 ,е ₂ ) группы SO (3 ,е 1 ,е ₂ ) . Алгебра Ли so (2 ,е 2 ) задается генератором т 2 ( е 2 ) и представляет собой либо вращения, либо псевдовращения, либо галилеевские бусты при е 2 = 1 , - 1 , 0 соответственно.

Калибровочные преобразования в декартовых координатах выглядят так ф‘ — G (е 1 ’е 2)( Хц) ф’

А ' ц ( е 1 ’е 2 ) — G ( е 1 ’е 2 )( Х ц ) д ц G ^- 1 ( е 1 ’е 2 )( Х ц )+

+ G ( е 1 ’е 2 )( Х ц ) А ц ( е 1 ’е 2 ) G ^- 1 ( е 1 ’е 2 )( Х ц ) •      (44)

Набор моделей (42),(43) будем называть моделями с калибровочными симметриями Кэли-Клейна. Поля р ( е 1 ’ е 2 ) и В ц ( е 1 ’ е 2 ) инвариантны при калибровочных преобразованиях так же, как ρ и B µ .

Рассмотрим подробно разные варианты значений е 1 ’ е 2 . При е ² ₁ — 0 , е ² ₂ — 1 , р (0 ’ 1) — ф 1 имеем вместо (42)

6 . Локальные SO(3,е 1 ,е2) инвариантные модели

Обобщим формулы (6),(13) на случай действия группы SO (3 ,е 1 ,е ₂ ) . Вставляя е 1 ,е ₂ в матрицы П и А ц и производя замены

B ^   > B ^ ^{( е} 1 ’^е 2 ) — ^{П 1 ( е} 1 ’^е 2 ) ^д ц ^{П( е} 1 ’^е 2 ^{) +} + П - 1 ( е 1 ,е 2 ) А ц ( е 1 ,е 2 )П( е 1 ,е 2 ) —

•

B µ ¹

B µ ³

ε ₁ B _µ

B

ε ² 1 ε ² 2 B µ ³ ε ² 2 B µ ²

•

^А ц ^— A ^ Ti -->^А ц ^{( е} 1 ’ ^е 2 ) ^— A p T ^{( е} 1 ’ ^е 2 ) ’

L — ( д ц ф 1 ) ² - V ( ф 1 )+

• ^{+    (} F ^{( ф} 1 ) ^- 1) ^ф 1 [( ^В ц ) ⁺ ( ^В ц ) ]⁺ L YM ⁽⁰ ’ 1) • ⁽⁴⁵⁾

При выборе F ( ф 1 ) — 1 + M j| /ф 1 + f ( ф 1 ) появляются два массивных калибровочных поля B _µ ¹ и B _µ ³ с массой M _B и одно калибровочное поле B _µ ² остается без-массовым. Число степеней свободы в (45) должно быть равно девяти, так как у нас было три поля материи ϕ _i (по одной степени свободы на каждое поле), и три безмассовых калибровочных поля A ⁱµ (по две степени свободы на каждое). В (45) одна степень приходится на поле материи ϕ 1 , шесть – на два массивных калибровочных поля B µ ¹ и B µ ³ и две степени – на без-массовое калибровочное поле B µ ² . Отметим, что при выборе е ² ₂ — - 1 , поле В ц ³ имело бы мнимую массу.

При е ² ₁ — 1 , е ² ₂ — 0 (42) принимает вид

Dц — д ц + А ц —> D ^ ( е 1 ’ е 2) — д ц + А ц ( е 1 ’ е 2 ) (41)

в лагранжианах (34),(35) и добавив лагранжиан калибровочных полей L YM ( е 1 ’е ₂ ) , имеем в радиальных координатах

L —( д ц р ( е 1 ’е 2 )) ² + е 1 р ² ( е 1 ’е 2 ) [( В ц ) + е 2 ( В ц ) j

^- V ^{( р ( е} 1 ’ ^е 2 )) ⁺ L YM ^{( е} 1 ’ ^е 2 ^{) +}

^{+ (} F ^{( р ( е} 1 ’^е 2 )) ^- 1) ^{р 2 ( е} 1 ’^е 2 ) ( ^В ц ) ^{+ е} 2 ( ^В ц )    ^—

— (дцр (е 1 ’е 2))2 + р 2( е 1 ’е 2) х х (е 1 + F(р(е 1 ’е2)) - 1) [(ВХц)2 + е2 (Вц) 2] -

^- V ^{( р ( е} 1 ’^е 2 )) ⁺ L YM ^{( е} 1 ’^е 2 ) ⁽⁴²⁾

L ^— ( ^D ц Ф ) 1 ⁺ ( ^D ц Ф ) 2 ^- V ^{( ф} 1 ^{+ ф 2 ) +} L YM ⁽¹ ’ ^{0) +}

• +    ( F ( Ф 1 + Ф 2 ) - 1 )( Ф 1 + Ф 2 )( в ц ) 2 • (46)

При выборе F ( ф 1 + ф 2 ) — 1 + м В / ( ф 1 + ф 2 ) + f ( ф 1 + ф 2 ) имеем одно массивное калибровочное поле B _µ ¹ с массой M _B и два безмассовых калибровочных поля. В этом случае со степенями свободы также все в порядке, если заметить, что в лагранжиан (46) входит только комбинация ф ² ₁ + ф ² ₂ — р ² (1 ’ 0) и степеней свободы, таким образом, всего восемь.

При е ² ₁ — 0 , е ² ₂ — 0 имеем

L — ( д ц ф 1 ) ² - V ( ф 1 )+

• +    (F(ф 1) - 1) ф 1 (вц)²+ Lym(0’ 0). (47)

7. Механизм Хиггса

При выборе F ( ф 1 ) = 1 + м В /ф 1 + f ( ф 1 ) также получается одно массивное калибровочное поле B _µ ¹ с массой M _B и два безмассовых. В этом случае требуется более аккуратный подсчет степеней свободы. После приравнивания к нулю ε _i , в лагранжиане (43) имеем: два поля материи (две степени свободы) и три без-массовых калибровочных поля ( 3 х 2 = 6 степеней свободы). В (47) получаем одно поле материи (одна степень свободы), одно массивное калибровочное (три степени свободы) и два безмассовых калибровочных поля ( 2 х 2 = 4 степени свободы). Отметим, что в случаях (46),(47) контракция уменьшает первоначальное число степеней свободы на единицу.

Таким образом, специальный выбор функции F позволяет делать калибровочные поля массивными.

В случае локальной симметрии безмассовые голдстоуновские частицы, взаимодействуя с калибровочными полями, придают им массу [16]– [18]. Посмотрим, как работает механизм Хиггса в случае лагранжиана (43) с потенциалом (36). Выберем ва- куум в виде фо = ^,0, 0).

С помощью калибровочной группы SO(3, еi, е2) можно перевести вектор (ф, 0, 0) в любой произвольный вектор (ф 1,ф2,ф3). Это будет означать выбор калибровки ф 1 = ф. ф 2 = 0. ф 3 = 0. (49)

в которой лагранжиан (43) выглядит

L = ^{( д} ^ ^{ф ) 2} — V ^{( ф} ) ⁺ L YM ^{( е} 1 ^,е 2 ^{) +}

+ ( е 1 + F ( ф ² ) — 1 ) ф ² [ ( A1 ) ² + е 2 ( A^ ) ² ] . (50)

При малых отклонениях от вакуума ф = m + и , полагая, что F ( ф ² ) — 1 = f о + ^ f k u k и оставляя в лагранжиане только слагаемые второго порядка, имеем

L = ( д ^ и ) ² — 2 m ² и ² + L ym ( е 1 ,е 2 )+

• + m^ (е 1 + f0) [(A1)²+ е2(A)²] . (51)

8.    Лагранжиан полей Янга-Миллса

Сравнивая выражения (51) и предпоследнюю строчку (42) видим аналогичность набора массивных компонент калибровочных полей. Оставшаяся компонента хиггсова изоскаляра u оказывается массивной, а из (50) видно, что она взаимодействует с калибровочными полями в слагаемых порядка выше второго.

Лагранжиан калибровочных полей Янга-Миллса в SO (3) теории обычно выбирают следующим

L YM = ^— .^TrF ! v =

⁴ g ²

= — 4 g 2 [( F ¹ ) ² + ( ^F 2 ) ² + ( ^F 3 ) 2 ] . (52)

здесь F ^v = [ д _ц + А _ц , d v + A v ] -тензор напряженности полей Янга-Миллса. Поскольку форма Киллинга, используемая для построения (52), в случае алгебр Кэли-Клейна вырождена, будем искать L YM ( е 1 ,е 2 ) для SO (3 ,е 1 ,е ₂ ) в следующем виде

L YM ^{( е} 1 ^,е 2 ) = C ab F av ^{( е} 1 ^,е 2 ) F bv ^{( е} 1 ^,е 2 ) . ⁽⁵³⁾

где F ^v ( е 1 , е 2 ) = [ д ^ + А д ( е 1 , е 2 ) ,d v + A v ( е 1 , е 2 )] . Константы C _ab находим из условия калибровочной инвариантности лагранжиана (53). Преобразования тензора F ^v ( е 1 ,е 2 ) следующие

F ‘ v ( е 1 ,е 2 ) = G ( е 1 ,е 2 ) F ^ v ( е 1 ,е 2 ) G 1 ( е 1 ,е 2 ) .

При инфинитезимальных преобразованиях G ( е 1 ,е ₂ ) ^ I + a i T i ( е 1 ,е ₂ ) , a i « 1 это соотношение принимает вид

F ’ iv = F iv ^{+ £} ijk ^{( е} 1 ^,е 2 ) ^a j F kv ■ ⁽⁵⁴⁾

Анализ уравнений (53),(54) дает следующие решения при разных комбинациях параметров ε 1 , ε 2 . Для случая е ² ₁ = 0 , е ² ₂ = 0 лагранжиан выглядит

{ C ¹¹ ( ^F^^v ) ⁺ C ²² ( F 2 ^v ) , F^{1 v} = ^{0 ;}

L YM ⁽⁰ . ⁰⁾ =

1 C 33 ( F 3 v) ,             F 1 v ² =0 ■

Для случая е 1 = 0 , е 2 = 1

г m      { C ²² ( F ^{2 v} ) ,            F ^{1 2 17}

L YM ⁽⁰ . 1)= | c [( f^v ^{) 2} + ( f 3 v ^{) 2} ] ,f^ ² v

Для случая е ² ₁ = 1 , е ² ₂ = 0

{ C 11 ( F ^{1 v} ) .           F ^{1 v}

L YM ⁽¹ ’ ⁰⁾   | C [( f , 2 v ) ² + ( F 3 v ) ² ] , f 1 v

= ^{0 ;}

= 0 .

= ^{0 ;}

= 0 .

Отметим еще возможность строить лагранжиан полей Янга-Миллса из полей B ^ ( е 1 ,е ₂ ) , которые не преобразуются при калибровочных преобразованиях. Тогда с точки зрения калибровочной инвариантности нет никаких ограничений.

9.    Выводы

Предложен способ получения теорий с непо-лупростой калибровочной группой. Получена серия лагранжианов как с глобальной, так и с локальной изотопической инвариантностью относительно преобразований в двумерных пространствах Кэли-Клейна. Найдены лагранжианы калибровочных полей для этого случая. При записи в унитарной калибровке массивность калибровочных полей при подходящем выборе функции F ( р ) очевидна. Проиллюстрирована теорема Голдстоуна для случая глобальной симметрии SO (3 , е 1 , е ₂ ) . Для случая локальной симметрии рассмотрено действие механизма Хиггса, которое оказывается схожим со случаем обычной SO (3) теории.

В отличие от случая с простой калибровочной группой, описанные теории с неполупростыми группами SO (3 , е 1 , е 2 ) допускают как изначальную массивность калибровочных полей за счет выбора F ( р ) в (42), так и приобретенную посредством механизма

Хиггса. Интересным является тот факт, что оба варианта дают одинаковый набор массивных калибровочных полей, т.е. «ненужный», в связи с изначальной массивностью, механизм Хиггса, тем не менее, работает с тем же результатом.

В работе [10], используя несколько иной подход, был получен тот же набор массивных и безмас-совых калибровочных полей.

Работа поддержана программой «Фундаментальные проблемы нелинейной динамики» Президиума РАН.