Калориметрические исследования сегнетоэлектриков в порах металлических матриц

Структуры на основе упорядоченных матриц, заполненных сегнетоэлектриком, могут использоваться для изготовлении различных элементов микро- и наноэлектроники [1, 2]. Нарушение структуры в сегнетоэлектрических материалах ведёт к неоднородному распределению спонтанной поляризации, являющейся основным параметром в теории Ландау-Гинзбурга. На физические свойства таких структур оказывают влияние эффекты, связанные с размерами и геометрией сетки пор. Кроме того, существенную роль играют взаимодействия частиц со стенками матрицы и между собой. В совокупности эти факторы приводят к тому, что характеристики частиц в порах могут значительно отличаться от характеристик соответствующих объемных материалов.

Исследованию свойств сегнетоэлектриков в силикатных матрицах диэлектрическими и калориметрическими методами посвящен ряд работ: KNO ₃ [3, 4], NaNO ₂ [5], TGS [6]. Сообщалось о расширении температурного интервала существования сегнетоэлектрической фазы для частиц KNO ₃ в пористых стеклах [3], а также в тонких пленках KNO ₃ [7]. Основными причинами изменения свойств частиц в наноразмерных матрицах указываются: влияние размерных эффектов, взаимодействие со стенками пор и диполь-дипольное взаимодействие между частицами [8].

поле отдельных частиц экранировано, что ведет к изменению свободной энергии системы. В данной работе приводятся результаты исследования сегнетоэлектрических фазовых переходов в KNO ₃, NaNO ₂ и TGS в матрицах из пористого тантала методом дифференциальной сканирующей калориметрии (ДСК) [9].

• 2.    ХАРАКТЕРИСТИКА ОБРАЗЦОВ И МЕТОДИКА ЭКСПЕРИМЕНТА

Нитрат калия при комнатной температуре имеет ромбическую структуру (пространственная группа Pmcn ). Эту фазу часто обозначают как фазу II. При нагреве около 128 ^оС происходит переход в фазу I, имеющую разупорядоченную т ригональную кальцитоподобную структуру R 3 m . При охлаждении после прогрева выше 170 ^оС нитрат калия переходит из высокотемпературной фазы I в промежуточную фазу III с симметрией R3m и только при дальнейшем охлаждении – в фазу II. Фаза III существует в температурном интервале от 124 ^оС до 110 ^оС и является сегнетоэлектрической с P s = 12 мкКл/см² [10].

Нитрит натрия при комнатной температуре является сегнетоэлектриком со структурой, принадлежащей к объемно-центрированной ромбической группе. При Тo = 163 оС происходит сегнетоэлектрический фазовый переход, связанный с увеличением вероятности нахождения атомов азота справа или слева от плоскости симметрии xz. Эта плоскость перестает быть плоскостью симметрии, и симметрия кристалла понижается до полярной группы mm2, вдоль оси у возникает спонтанная поляризация. Частичное упорядочение групп NO2 сопровождается смещением атомов натрия вдоль оси у, дающим значительный вклад в спонтанную поляризацию (при Т =100°С Ps = 8 мкКл/см2). Особенность нитрита натрия заключается в том, что сегнетоэлектрическая упорядоченная фаза отделена от неупорядоченной параэлектрической фазы несоразмерной фазой, стабильной лишь в узком температурном интервале около 1 ^ 1,5 оС [11].

Триглицинсульфат ( TGS ) представляет собой классический сегнетоэлектрик с фазовым переходом второго рода. Выше температуры Кюри ( Т _о = 49 ^оС) кристалл TGS имеет моноклинную симметрию и принадлежит к центросимметричному классу 2/ m . Ниже Т _о кристалл принадлежит к полярной точечной группе 2 моноклинной системы (зеркальная плоскость исчезает). Полярная ось лежит вдоль моноклинной оси 2-го порядка. Одна элементарная ячейка кристалла TGS содержит более 100 атомов. Структура TGS сложна и представляет собой сетку молекул глицина CH ₂ NH ₂ COOH и тетраэдров SO ₄, связанных между собой водородными связями [12].

В качестве пористых матриц использовались объемно-пористые аноды от жидкостных танталовых электролитических конденсаторов (ЭТО), которые предварительно тщательно промывались. Средний размер пор определялся методом электронной микроскопии и составлял 2 – 20 мкм (рис. 1).

Для нитрата калия и нитрита натрия внедрение в матрицу осуществлялось из расплава, для чего кювета с сегнетоэлектриком прогревалась до температуры выше температуры плавления и предварительно прогретая матрица помещалась в расплав на 30 мин. Температура плавления KNO ₃–334 ^оС , NaNO ₂–271 ^оС. Для образцов TGS в связи с тем, что при нагревании выше 110 ^оС это вещество разлагается, внедрение осуществлялось из насыщенного водного раствора.

При исследовании сегнетоэлектриков в металлических матрицах нельзя пользоваться электрическими методами, поэтому был использован калориметрический метод. Метод дифференциальной сканирующей калориметрии (ДСК) яв-

ТМ-1000_1298          2012.10.09          D2.0         200 um

Рис. 1. Фотография поверхности танталовой матрицы, полученная с помощью электронного микроскопа Hitachi TM-1000

ляется наиболее чувствительным способом определения величины изобарной теплоёмкости вещества в широком температурном диапазоне и позволяет определять не только температуру фазового перехода, но и степень его размытости. В методе ДСК имеются две измерительные ячейки: одна предназначена для исследуемого образца, в другой находится эталонный образец. Экспериментально измеряется временная зависимость разницы температур между исследуемым и эталонным образцами.

Экспериментальная установка (см. рис. 2) позволяла проводить измерения в температурном интервале от 20 до 300 оС. Скорость нагрева-охлаждения составляла 2 град/мин, разрешение – порядка 5 мкВт. Измерения осуществлялись в автоматическом режиме с записью на компьютер с интервалом в 1 с. Температура образца фиксировалась с точностью 0,1 град.

Данная измерительная система позволяет в автоматизированном режиме осуществлять сбор

Компьютер и ZETLab

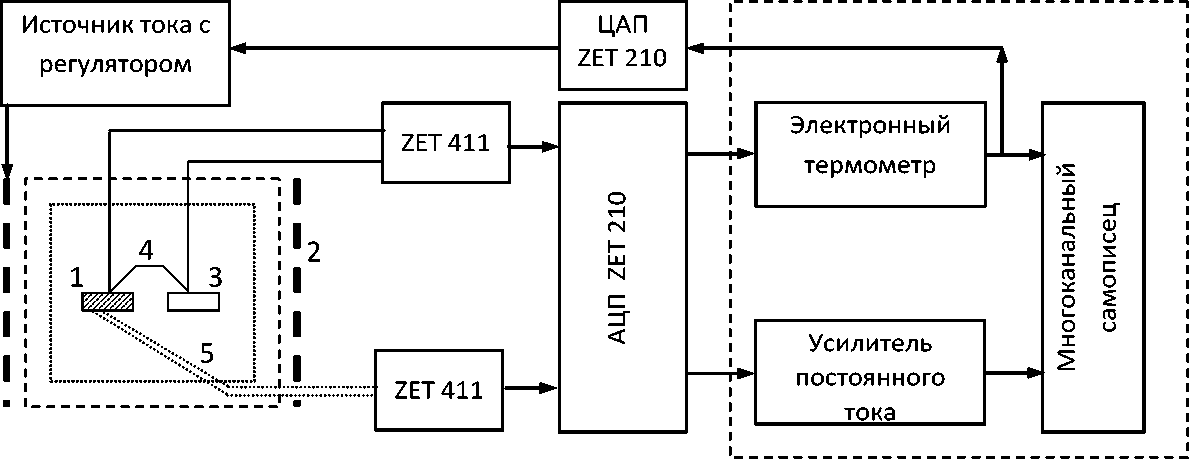
Рис. 2. Схема измерительной системы ДСК:

1 – исследуемый образец, 2 – термостат, 3 – эталонный образец, 4 – дифференциальная термопара, 5 – термопара для контроля температуры образца

данных, скоростную оцифровку усиленного сигнала и его дальнейшую программную обработку в среде ZetLab . ZET 210 – модуль АЦП/ЦАП (с частотой дискретизации до 400 кГц) функционирует в режиме непрерывного ввода/вывода аналоговых и цифровых сигналов в память ПЭВМ. ZET 411 – предварительный усилитель, предназначенный для повышения чувствительности сигнала термопары. Коэффициенты усиления (КУ) – фиксированные 10, 100 или 1000. Для усиления сигнала дифференциальной термоэдс также использовался усилитель ZET 411, что позволяло фиксировать разность температур исследуемого и эталонного образцов Д Т <  0,01°С.

• 3.    ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

Результаты измерений поликристаллического нитрата калия и нитрата калия в матрице из пористого тантала методом сканирующей калориметрии при охлаждении после первого прогрева образцов до температуры 180 оС приведены на рис. 3.

Как видно из рис. 3, пики теплоёмкости для поликристаллического образца соответствуют температурам фазового перехода, известным по литературным данным [10]. Металлическая матрица слабо влияет на температуру фазового перехода I ^ III и в значительно большей степени сказывается на переходе III ^ II, приводя к по-

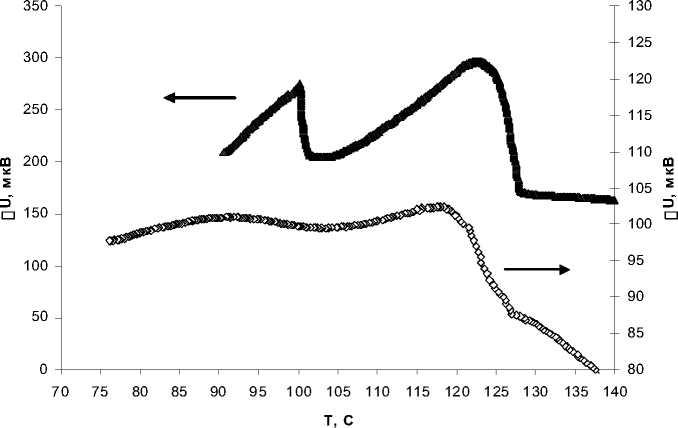
Рис. 3. Изменения сигнала ДСК для поликристаллического KNO ₃ ( ) и KNO ₃ в порах ( ) металлической матрицы

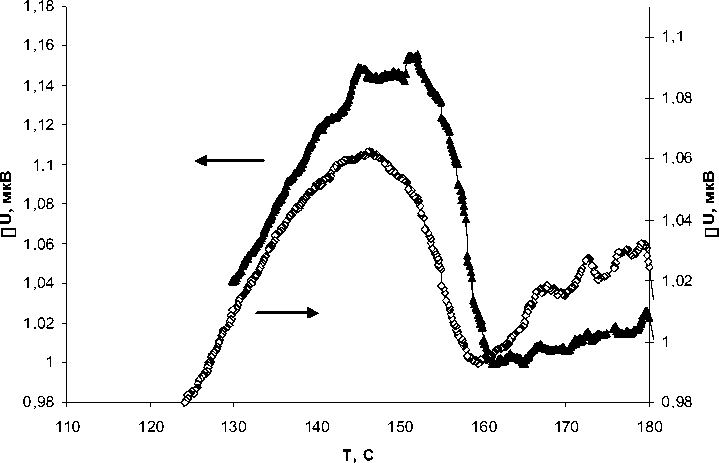
Рис. 4. Температурная зависимость термоэдс для объемного ( ▲ ) и внедренного в матрицу ( ) NaNO ₂

нижению температуры перехода и его размытию.

Результаты калориметрических исследований для образцов поликристаллического объемного NaNO ₂ и NaNO ₂ в металлической пористой матрице показаны на рис. 4. Из представленных графиков следует, что для NaNO ₂ в матрице наблюдается некоторый сдвиг температуры фазового перехода в область более низких температур А Т ~ 2 о С.

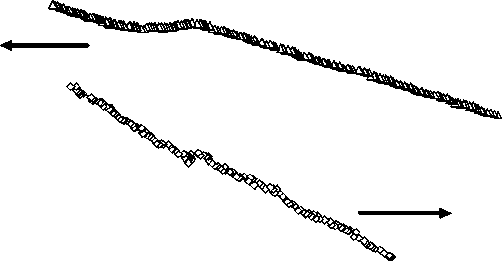
Температурный ход термоэдс для объемного TGS и TGS в танталовой проводящей матрице представлен на рис. 5.

Как следует из графиков, пики термоэдс для поликристаллического TGS и TGS , внедренного в проводящую матрицу, совпадают с точностью до 0,5 ^оС. Следовательно, на настоящий момент нельзя сказать, что температура фазового перехода для TGS существенно зависит от того, объемный сегнетоэлектрик или внедренный в матрицу.

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Влияние проводимости на сегнетоэлектрические свойства кристаллов рассматривалось в работах [13-17]. Наличие свободных носителей заряда приводит к изменениям температуры Кюри, температурного гистерезиса, спонтанной поляризации, спонтанной деформации диэлектрических и пьезоэлектрических свойств. В [14] было показано, что добавочная энергия, связанная с возбуждением неравновесных носителей, равна nE_g ( P ), где n – концентрация, а E_g – ширина запрещенной зоны, так что свободная энергия кристалла записывается в виде

F = F o + a P 2 +( Р /2) P +... + nE_g ( P ). (1)

Это ведет к снижению температуры перехода на величину

А T

А E C

g n

кP2   ’

s

где А E_g - изменение ширины запрещенной зоны при фазовом переходе первого рода, С – константа Кюри – Вейсса.

При микроскопическом подходе полагают, что поле каждого иона независимо экранируется носителями. В терминах теории Гинзбурга-Ан-дерсона-Кокрана это приводит к уменьшению лоренцевского поля (а также макроскопического поля) и соответственно сдвигает температуру, при которой частота поперечной оптической моды колебаний обращается в нуль. Расчет температурной зависимости to ТО с учетом экранирования был выполнен в ряде работ [15-17].

В случае сегнетоэлектрических композитов, состоящих из полярных частиц, необходимо учесть электрические взаимодействия между отдельными частицами. В этом случае, свободная энергия системы сегнетоэлектрических частиц будет включать суммы энергий системы частиц и энергии диполь-дипольного взаимодействия между частицами А F dd , которая имеет вид [8]:

^{А F}dd = ZK i - j V V

p i p j

* *

3 ³ ij

3(rij p* Xri, p*) rj

^dVi^dVj , (3)

где V_i , V_j и p _i , p _j – объёмы и поляризация частиц сегнетоэлектрика, соответственно, r_ij – является экстраполяционной длиной, которая определяется распределением частиц в образце.

Учет А F dd ведет к тому, что температура фазового перехода системы связанных частиц T_o по сравнению с температурой фазового перехода в изотропных образцах T _o будет определяться соотношением

ш

Т, С

tn

Рис. 5. Температурная зависимость термоэдс для объемного ( ) и внедренного в матрицу ( ) TGS

T o

= T + — A F,, o              dd

^αо          ^,

Энергия диполь-дипольного взаимодействия A F dd в зависимости от расположения и ориентации дипольных моментов частиц может иметь как положительный, так и отрицательный знак. В металлической матрице диполь-дипольным взаимодействием A F dd можно пренебречь.

Однако как для металлических, как и для диэлектрических матриц надо учитывать другие взаимодействия. Микро- и особенно нанокомпозиты обладают развитой сетью внутренних границ раздела, градиентов напряжений и химических потенциалов между частицами и стенками матрицы, которые приводят к процессам межфазного взаимодействия в системе. Это обусловлено тем, что на межфазной границе вследствие разного состава и строения соприкасающихся фаз и из-за различия в связях поверхностных атомов и молекул одной и другой фазы существует ненасыщенное поле межатомных сил. Для учета поверхностных явлений в свободную энергию необходимо добавить слагаемое A F s , учитывающее поверхностный вклад

AFs = Е J ^d^+ Е J ^dN+ Е J ^MSi

Si                           Si                            Si, где б i - поверхностное натяжение, Si - площадь поверхности частицы, Д i, Ni - химический потенциал и число частиц в системе i-го компонента, ^i- электрический потенциал, Si - плотность поверхностного заряда.

Слагаемое A F s дает большой вклад в свободную энергию систем с высокоразвитой поверхностью межфазных границ. Образование на межфазной границе двойного электрического слоя в результате эмиссии электронов или экранирования спонтанной поляризации, а также ориентации диполей в поле поверхностных сил приводит к появлению электрических поверхностных явлений: поверхностной проводимости, поверхностного электрического потенциала и т.д. Эти причины уменьшают эффективное электрическое поле в частицах, что может приводить к изменению спонтанной поляризации и сдвигу фазовых переходов.

Учитывая, что механические напряжения и зажатие частиц в порах для исследуемых сегнетоэлектриков должны приводить к повышению температуры Кюри [18], единственным механизмом влияния на свойства сегнетоэлектрических частиц в металлических матрицах является экранирование спонтанной поляризации, и образование двойного слоя на границе раздела.

5. ЗАКЛЮЧЕНИЕ

Методом дифференциальной сканирующей калориметрии исследованы фазовые переходы для объемных сегнетоэлектриков и сегнетоэлектриков в порах металлических матриц (2-20 мкм). Как показали исследования, для частиц ионных кристаллов KNO3 и NaNO2 в матрице наблюдается понижение температуры фазовых переходов, подобно тому, как это происходит в сегнетоэлектриках-полупроводниках. Полученные результаты можно объяснить экранированием спонтанной поляризации за счет образования двойного слоя на границе раздела сегнетоэ-лектрик-металл. Отсутствие сдвига температуры фазового перехода для TGS может быть связано с тем, что это молекулярный кристалл с очень слабой проводимостью и меньшей по сравнению с KNO3 и NaNO2 спонтанной поляризацией (при Т = 20°С она составляет = 2,8 мкКл/см2).

Работа выполнена при поддержке Минобрнауки РФ (проект № 2014/424).