Камертонный вибровискозиметрический датчик для исследования термостимулированных процессов в жидкостях

мы, r – механическое сопротивление колебательной системы, k – приведенная жесткость колебательной системы, х – отклонение колебательной системы от положения равновесия, F(t) – вынуждающая сила, приложенная к колебательной системе. Данное уравнение достаточно хорошо описывает поведение вибровискозиметра, работающего в режиме вынужденных колебаний с малой амплитудой [1].

При использовании в качестве зонда вискозиметра шарика диаметром d , погруженного в жидкость с динамической вязкостью п, плотностью р, и достаточно удаленного от стенок кюветы, на основании решения уравнения Навье-Стокса можно найти силу сопротивления F_c , действующую на колеблющийся с частотой ю шарик [4,5]:

F = г • ¹ c r з

д x    д² x

— + m— 7 д t      д t ²

где r _з – механическое сопротивление зонда в жидкости, m – присоединенная масса жидкости. При

этом механическое сопротивление и присоединенная масса выражаются следующим образом:

r₃ = 3 nnd

1 + d- (юР/2 n)1/2

n 3        ( 2 np/to ) ^1/2

m = —d p + 9 -^-У-—

12 P d

Параметры r _з и m могут быть определены в результате экспериментальных измерений резонансной частоты to , амплитуды А и фазы

ф вынужденных колебаний зонда на воздухе и при его погружении в жидкость [6]. В этом случае динамическая вязкость и плотность жидкости вычисляются путём одновременного решения уравнений (3) и (4). Необходимо отметить, что это возможно только при сферической форме зонда.

Точность определения динамической вязкости и плотности с помощью вибровискозиметра существенно зависит от его конструктивного исполнения, в том числе от эффективности его виброизоляции от внешней среды.

Для анализа влияния конструкции на параметры вибровискозиметра рассмотрим его упрощенную механическую модель (рис. 1), включающую в себя массивное основание массой М с возбудителем колебаний (например, электромагнитным), зонд массой m и упругую безмассовую связь k между ними. Z – комплексное механическое сопротивление связи между основанием и землей (бесконечной массой).

Рассмотрим случай, когда Z бесконечно велико, т.е. связь между основанием и землей отсутствует (вибродатчик находится в свободном пространстве).

Пусть со стороны основания на зонд действует сила               . При этом со стороны зонда на основание будет встречно действовать такая же сила Fm. В этом случае при движении зонда с ускорением аm основание вибродатчика будет двигаться с ускорением т .

Под действием данной гармонической силы F_M зонд совершает механические колебания амплитудой h_m и частотой ω относительно положения равновесия:                  .

m

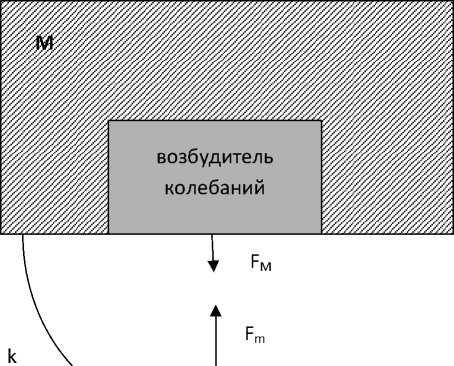
Рис. 1. Упрощенная механическая модель вибровискозиметра

В этом случае максимальная скорость его движения            .

Основание также совершает механические колебания. При этом с учетом закона сохранения количества движения максимальная скорость т основания составит           с амплитудой колебаний            .

™ М

С учетом того, что кинетическая энергия пропорциональна массе колеблющегося тела и квадрату его скорости, получаем отношение кинетической энергии основания EM к кинетической энергии зонда Em:

Ем т

.

Таким образом, при конечном значении массы основания общая энергия возбудителя будет перераспределяться между основанием и зондом обратно пропорционально отношению их масс. При процесс передачи энергии от возбудителя на основание вибродатчика прекращается, и вся энергия передается вибрирующему зонду.

В реальных условиях вибродатчик не находится в свободном пространстве, а его основание связано с бесконечной массой (землей) через промежуточные конструктивные элементы: вибро – и термоизоляцию, внешний корпус, позиционер.

Данные элементы, в общем случае, обладают как упругими (реактивными), так и вибропоглощающими (активными) свойствами. Величина конечного механического сопротивления Z будет определять потери энергии EM возбудителя механических колебаний. Механическое сопротивление может существенно зависеть от температуры окружающей среды, нестабильности во времени механических характеристик элементов вибро-и термоизоляции, конструктивных соединений. Указанные обстоятельства приводят, при постоянстве возбуждающей силы FM, к нестабильности амплитуды h колебаний зонда во времени, т.е. ограничивают разрешающую способность и чувствительность вибродатчика.

Улучшить метрологические характеристики вибродатчика можно, если уменьшить передачу энергии EM на основание вибродатчика. Этого можно достичь либо за счет значительного увеличения массы основания в рассмотренной механической модели, либо за счет введения дополнительного колебательного звена, соединенного с основанием вибродатчика.

Рассмотрим подробнее вторую возможность, которая схематически показана на рис. 2 для случая вибродатчика в свободном пространстве.

В отличие от рис. 1 здесь введен дополнительный элемент – «компенсатор» с массой m₁ и упругой безмассовой связью k₁ между компенсатором и основанием M. Компенсатор находится вне зоны действия возбудителя. Резонансные частоты колебаний зонда ω _m и компенсатора ω _m1

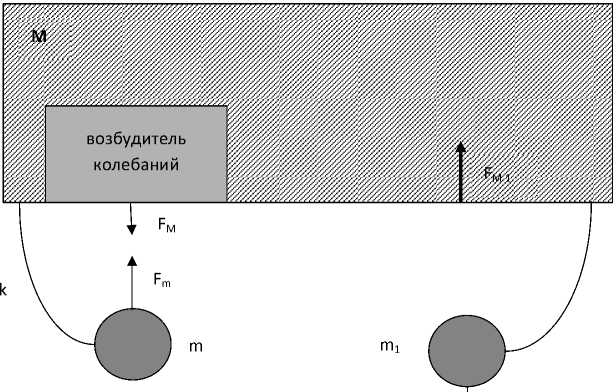
F m 1

Рис. 2. Колебательная система с компенсатором

k k равны, соответственно: to m = . —, m m 1 = — .

^{m m} 1

Для компенсации необходимо выполнение условия равенства резонансных частот to m = to m 1 = to . В этом случае при колебаниях зонда под действием возбуждающей силы F_M с амплитудой h_m и частотой w компенсатор, за счет колебаний основания вибродатчика, также начнет колебаться с данной частотой и установившейся амплитудой h_m1. При этом колебания зонда и компенсатора происходят в противофазе.

Найдем результирующую силу, действующую на основание при установившихся колебаниях зонда и компенсатора:

Из (5) и (9) получим: