Капиллярная модель древесных стволов
Автор: Вернигоров Юрий Михайлович, Кипнис Иосиф Аншелевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 6 (67) т.12, 2012 года.
Бесплатный доступ
Исследуется механизм подъёма воды в стволах деревьев силами поверхностного натяжения в капиллярных каналах различного диаметра и конфигурации.
Капилляр, ствол, ксилема, транспирация, растение
Короткий адрес: https://sciup.org/14249899
IDR: 14249899 | УДК: 581.1
Текст научной статьи Капиллярная модель древесных стволов
Введение. Структура водопроводящих путей и механизм передвижения воды различны не только в растениях разных видов, но и в пределах одного растения в различных его органах. Чтобы понять, как образуется восходящий транспирационный поток воды в сосудистых растениях, необходимо построить физические модели этого процесса для каждого органа, учитывающие его анатомическое строение, что позволит понять процесс продвижения воды в тканях органов и в растении в целом.
Предположение в [1] о равенстве радиусов всех капилляров в растении достаточно идеализировано. Однако позволяет сделать выводы о возможном механизме образования специфической формы растений капиллярными системами. Кроме того, можно предположить, что поверхностное натяжение водного мениска в капиллярах проводящего пучка мезофилла порождает движущую силу, создающую восходящий транспирационный поток.
В качестве изучаемого объекта выберем стебель древесного растения. Анатомическое строение его клеточных структур, водопроводящих элементов и тканей подробно описано и иллюстрировано в работах [2—4]. В клеточных тканях растений различают ближний и дальний транспорт воды и водных растворов. Ближний транспорт осуществляется по апопласту и эндопласту, по клеточным стенкам, и, вследствие высокого сопротивления клеточных и межклеточных тканей движению воды, эффективен только на малых расстояниях — до 0,2 мм. Дальний транспорт, вертикальное продвижение воды в стволах деревьев, осуществляется специализированными капиллярными водопроводящими тканями: трахеидами и сосудами, вытянутыми вдоль направления подъёма воды. В хвойных растениях вертикальная капиллярная структура представлена исключительно трахеидами, занимающими свыше 90 % объёма древесины. В древесине лиственных пород такую функцию выполняют сосуды и трахеиды, в том числе сосудистые и волокнистые [4]. Такая водопроводящая капиллярная ткань носит название ксилемы.
Различают первичную ксилему, образующуюся из клеток прокамбия, и вторичную, порождаемую клетками камбия. Прокамбий образует протоксилему — растущие в длину трахеиды кольчатого и спирального типа, и метаксилему, образующуюся по окончании роста органа в длину. Трахеиды метаксилемы, как правило, пористые, но бывают сетчатого и спирального вида с тесно сближенными витками спирали вторичной стенки [2, 3]. В стволе дерева трахеиды в годовых кольцах обычно собраны в радиальные ряды, в которых крупные первичные трахеиды протоксилемы выполняют в основном проводящую функцию. Крупные трахеиды постепенно сменяются более мелкими с толстыми стенками. Они являются упрочняющей механической структурой и не участвуют в проведении воды. У ранних трахеид средний радиальный размер составляет для лиственных и хвойных пород соответственно 52 и 40 мкм, а у поздних трахеид — 22 и 20 мкм. Тангенциальный размер в обоих случаях примерно 30 мкм. Средняя длина трахеид у лиственницы
2,6 мм, у сосны — 2,8 мм, а у ели — от 2,6 до 5 мм. На радиальных стенках, особенно у концов ранних трахеид, имеется от 70 до 90 крупных окаймлённых пор с округлыми отверстиями. В поздних трахеидах поры могут быть и на тангенциальных стенках. Диаметр окаймлённых пор колеблется от 8 до 31 мкм, а диаметр отверстии в порах — от 4 до 8 мкм [4]. В смежных трахеидах поры образуются строго друг против друга. Трахеиды в последовательной цепочке перекрываются концевыми частями примерно на одну треть своей длины. Смежные кольчатые и лестничные трахеиды проводят воду в горизонтальном направлении через проницаемую плёнку, а пористые — через рыхлую замыкающую плёнку поры или через пору с торусом. Большое сопротивление движению воды через одиночную пору компенсируется множеством одновременно проводящих воду пор в стенке трахеиды.
У хвойных растений крупные окаймлённые поры располагаются только на радиальных стенках, и благодаря расположению трахеид соседних рядов в разных уровнях трахеиды соседних радиальных рядов могут передавать воду друг другу, обеспечивая её подъём.
В деревьях лиственных пород в капиллярном подъёме воды кроме трахеид участвуют сосуды, которые занимают у разных пород от 10 до 55% объёма ствола. Сосуды образуются путём соединения концов пористых трахеид с последующей их перфорацией. При этом образуются вертикальные трубки, длина которых может достигать нескольких метров. У сосудов ранней зоны диаметр может быть от 200 до 400 мкм, а сосудов поздней зоны — от 270 до 580 мкм. Перфорации между объединёнными трахеидами иногда сохраняют форму пор, но чаще они разрушаются, и на месте замыкающей пору плёнки образуется перфорированная пластинка с одним большим (реже — с несколькими меньшими) отверстием, что до минимума снижает сопротивление току воды. Сосуды в стволе проходят в большинстве своём волнообразно изогнуто, что позволяет им контактировать между собой. Окаймлённые поры на стенках сосудов чаще всего располагаются диагональными рядами (очередная поровость) и через эти поры сосуды сообщаются друг с другом и с трахеидами.
По мере роста дерева часть ксилемы образует не проводящее и не содержащее воду ядро (спелую древесину), а восходящий ток воды происходит по капиллярам ксилемы более поздних годичных слоёв, носящих название заболони. Обычно заболонь включает ксилему, образовавшуюся за 2—3 последних вегетационных сезона [3], но по данным [4] в раннем возрасте древесина всех пород состоит только из заболони и с течением времени начинается образование ядра. Например, у дуба ядро образуется на 8—12-й год, а заболонь бывает узкой, у сосны ядро образуется в возрасте 30—35 лет, что обусловливает наличие широкой заболони. В пределах самой заболони наиболее активно (до 80—90 % объёма) проводит воду ксилема последнего вегетационного периода. Это, например, показано в экспериментальных исследованиях сокодвижения в дубе черешчатом [5].
Как было показано выше, в капиллярной системе ксилемы в контакте могут находиться трахеиды и сосуды разных высот и диаметров.
Поэтому стоит задаться вопросом о том, как изменится продвижение воды в капиллярах, если капиллярная трубка будет разного диаметра и разной формы, что и является целью данной работы.
Теоретическая модель. Допустим, что мы имеем капиллярную трубку, нижняя часть которой имеет радиус r 1 , а радиус верхней r 2 < r 1 (см. рис. 1). При этом высота нижней части, выступающая над поверхностью воды, равна h . Обозначим общую высоту подъёма воды в капиллярной трубке через H , а высоту подъёма её в капилляре радиуса r 2 через x . Уравнение, описывающее подъём воды в такой трубке, будет выглядеть следующим образом:
n r 12 p gh + n r 22 p gx = 2 n r 2 o cos a , (1)
откуда:
x = 2 ocosa/ r 2 p g - h ( r / r 2 2 ) = h 2 - h ( r ^ / r 2 2 ) , (2)
где h 2 — высота подъёма воды в капилляре радиуса r 2 , если бы не было нижнего капилляра.
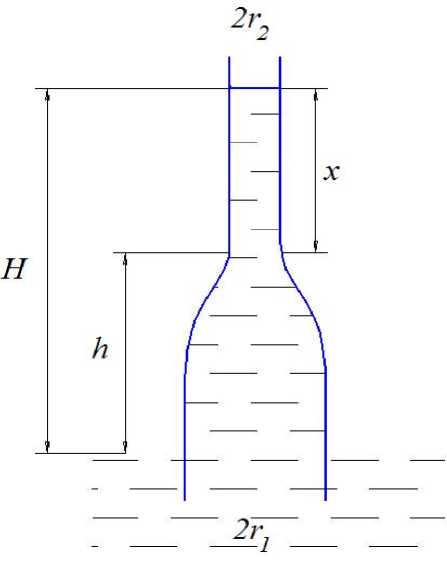
Рис. 1. Модель капилляра переменного сечения при r 2 < r 1
Общая высота подъёма воды в капиллярной трубке равна:
H = h + x = h + h 2 - h ( r / r ) = h 2 + h ( 1 - r 12 / r 2 2 ) (3)
Из (3) следует, что если r 2 = r 1 , то H = h 2 , как и в случае одиночного капилляра радиуса r 2 .
Если r 1 > r 2, то разность 1 - r 12 / r 2 2 отрицательна и высота подъёма воды в капилляре рассматриваемой модели меньше, чем в цилиндрическом капилляре радиуса r 2 . Это связано с тем, что с увеличением радиуса r 1 в нижней части капиллярной трубки объём поднимаемой в капилляре воды увеличивается, а сила поверхностного натяжения в капилляре радиуса r 2 остаётся постоянной. При некотором значении r 1 вес воды в капилляре большего радиуса станет равным силе поверхностного натяжения, и вода при дальнейшем увеличении этого радиуса будет опускаться до величины h 1 , соответствующей максимальной высоте подъёма воды в капилляре большего радиуса. Высота h , на которой это происходит, является критической.
Если r 1 < r 2, то разность 1 - r 12 / r 2 2 имеет положительный знак и высота подъёма воды H стремится по мере увеличения r 2 к величине h 2 + h , что физически нереально. Этому случаю соответствует модель на рис. 2. Уравнение, описывающее подъём воды в таком капилляре, будет иметь вид:
п r 2 2 p gh + п r 12 p gx = 2 п r 1 o cos a, (4)
а высота подъёма воды H в этом случае составит
H = h 1 + x = h 1 + h - h ( r 2 / r 12 ) = h 1 + h ( 1 - r 2 2 / r 12 ) (5)
где h 1 — высота подъёма воды в вертикальном капилляре радиуса r 1 . если бы не было нижнего капилляра. Из выражения (5) следует, что при r 1 = r 2 имеем H = h 1 .
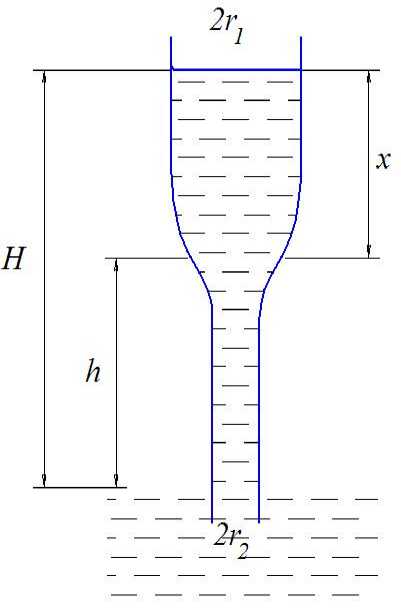
Рис. 2. Модель капилляра переменного сечения при r 1 < r 2
При r 1 > r 2 высота подъёма воды в капилляре стремится к h 1 + h . Действительно, с увеличением r 1 объём воды в этой части капилляра увеличивается (в нижней части меньшего радиуса объём остаётся постоянным), но сама величина h 1 уменьшается, так как сила поверхностного натяжения обратно пропорциональна радиусу капилляра. И общая высота подъёма воды H в этом случае уменьшается. При r 1 < r 2 физический смысл теряется и следует пользоваться выражением (3).
Соотношения (3) и (5) позволяют определить условия, при которых вода в капилляры другого сечения (расположенные выше) поступать не будет. Полагая в этих выражениях x = 0, получим для первой и второй моделей соответственно:
h 2 = h ( r i / r H h = h 2 ( r 2 / Г 2 ) = h i ( r / Г ) (6)
h i = h ( r / Г 2 H h = h i ( r 2 / r ) = h 2 ( r / r ) (7)
Предположим теперь, что в первой модели над цилиндрическим капилляром радиуса r 1 имеется n цилиндрических капилляров одинакового радиуса r 2 (рис. 3), вписанных в окружность радиуса r 1 .
Определим высоту x подъёма воды в n капиллярах и общую высоту подъёма воды H . Уравнение, описывающее подъём воды в n капиллярах, может быть записано в виде:
n r12pgh + nn r2pgx = n2n r2a cos a ,(8)
откуда высота подъёма воды в них равна x = h2 - - h (ri2 / r2),(9)
2n 12
а общая высота подъёма воды H равна
H = h + x = h + h fl - — (r2 / r1))
2 ( П 12 '
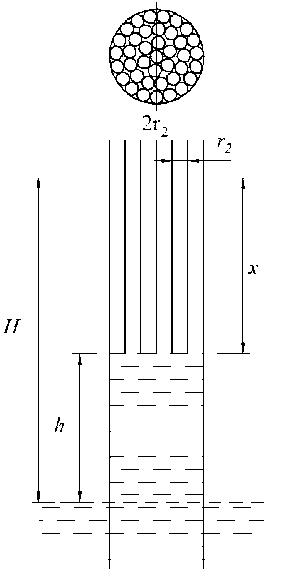
Рис. 3. Модель перехода капилляра в систему из n капилляров
Из (10) следует, что при r1 = r2 (n = 1) получим H = h2. В общем же случае высота подъёма воды H зависит от количества капилляров и от отношения r12 /r22 . С увеличением n высота подъёма воды возрастает, а с увеличением отношения радиусов высота подъёма воды уменьшается. Критическое значение высоты hкр, при котором вода в тонкие капилляры не поступает (x = 0), определяется из (9) и равно hkp = nh2 * / *22). (11)
Равенство (11) позволяет утверждать, что при данном соотношении количества капилляров и их радиусов, суммарная сила поверхностного натяжения их менисков достаточна только для поддержания воды в капилляре радиуса r 1 на высоте h кр .
Действительно, при условии, что n принимает значения 1 и 2, а r 2 = r 1 /2 (рис. 4), из (10) можно определить высоты подъёма воды для каждого значения n:
Hn = 1 = h 2 + h ( 1 - ( 4 * 22 / r 22 ) ) = h 2 — 3 h ,
H . = h + h 1 1 - -(4 r 2 / r 2) I = h - h .
П=2 2 2* 2 22
Разность высот подъёма равна:
H-o - H-1 = h - h — h + 3h = 2h . n = 2 n = 1 22
Критические значения h кр для n = 1 и n = 2 соответственно равны:
крп = 1 2 ( * 2 I 4 1 2 ) 4 2 ,
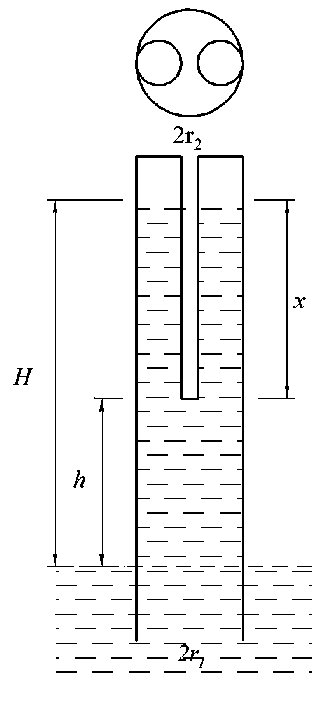
Рис. 4. Модель перехода капилляра в систему из n = 2 капилляров
Из последних соотношений, очевидно, что при увеличении количества капилляров уровень воды в них поднимается, а критическое значение h увеличивается.
Для второй модели (рис. 5) в случае n капилляров уравнение подъёма воды может быть записано в виде:
л п r 22 p gh + п r12pgx = 2 п r 1 o cos a, (12)
а высота подъёма воды H запишется в виде:
H = h 1 + h ( 1 - л ( r / r ) ) . (13)
Из уравнения (13) следует, что при r 2 = r 1 ( n = 1) имеем H = h 1 . При увеличении n и отношения r 1 /r2 и выполнении условия л ( r 2 2 / r 12 ) = 1 общая высота подъёма воды не будет превосходить h i .
Используя уравнение (13) можно определить высоты подъёма воды для n = 1 , n = 2 и r 2 = r 1 /2 (рис. 6):
н л = 1 = h + h ( 1 -( r 22 / 4 r 22 ) ) = h i + 4 h ,
H = h h . + h (1 - 2 ( r 2 / 4 r 2 = h + 1 h ,
Л=2 1 2 2 1
Разность высот подъёма равна:
H . - H . = h. + -h - h. - -h = — h .
л=2 л=11 14
Таким образом, уровень воды при увеличении количества капилляров уменьшается, что объясняется увеличением объёма воды, поднимаемой верхней частью капилляра радиуса r 1 при сохранении в нём постоянной силы поверхностного натяжения.
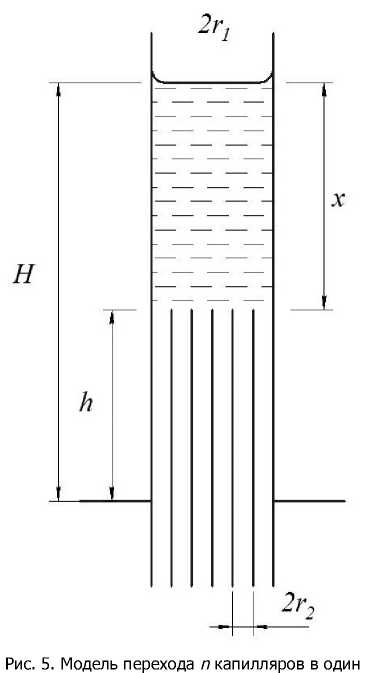
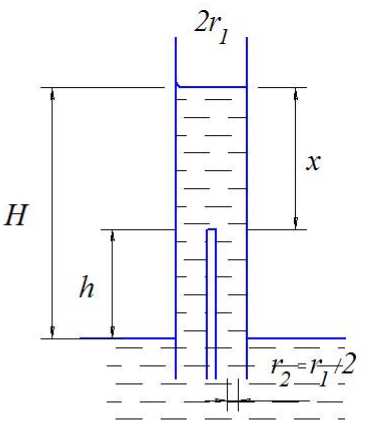
Рис. 6. Модель перехода системы из n = 2 капилляров в один
Аналогом капилляра переменного сечения в живой природе могут служить трахеи (сосуды) ксилемы. При слиянии конечных (торцевых) стенок клеток, образующих трахею происходит перфорация (разрыв) стенки с образованием перфорационной пластинки, имеющей одно или несколько сквозных отверстий ([2], стр. 88, [3], стр. 117, 118). При этом внутренняя часть образовавшегося капилляра частично перекрывается.
В связи с этим представляет интерес рассмотреть подъём воды в капилляре радиуса r 1 , изображённом на рис. 7, в котором в поперечном сечении имеются перегородки с отверстием радиуса r 2 . Примем для определённости, что высоты первого вертикального участка капилляра над поверхностью воды и всех последующих сегментов одинаковы и равны h , толщина перегородки l □ h , а сама величина h много меньше критического значения, определяемого из формул (6) и (7).
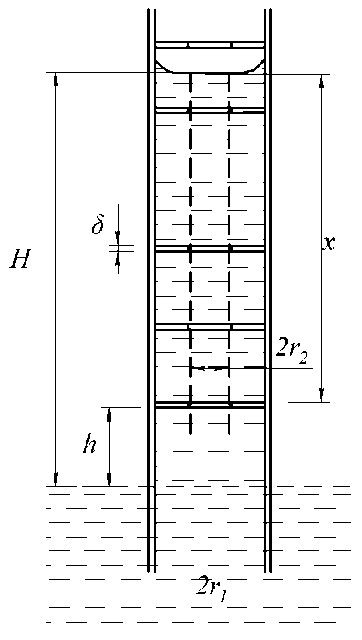
Рис. 7. Модель капилляра с внутренними перегородками
Уравнение, описывающее подъём воды в таком капилляре, может быть записано в следующем виде:
nr cgh + nr2cgx = 2 n n r 1 y cos a (14)
Физический смысл записанного уравнения заключается в следующем. В рассматриваемом капилляре в каждом сегменте, за исключением первого (нижнего), часть веса воды компенсируется силами упругости перегородки, на которую она действует. Не скомпенсированными остаются только вес столба жидкости с радиусом r 2 (см. пунктир на рис. 7), а также вес жидкости в самом нижнем сегменте. Это нашло отражение в левой части уравнения (14). Сила же поверхностного натяжения в данном случае пропорциональна большему радиусу r 1 . Получается, что в рассматриваемой структуре большая сила поверхностного натяжения обеспечивает подъём воды в капилляре (условном) с меньшим радиусом.
Из (14) следует, что nr22cgx = 2nrx y cos a + nr cgh ,(15)
откуда r2
x = (2 nr ycosa)/(nr22cg)-(nri2cgh)/(nr2cg) = (ryycosa)/(r^cg)-h^ = hr /r2 -h^ (16) r2
Общая высота подъёма воды в таком капилляре будет равна:
2 I
Ноб = h + h2r /Г2 -hr^ = h2ri /Г2 + h 1 -4
r2 I
Из (17) следует, что при r 1 = r 2 H об = h 2 , что соответствует подъёму воды в одиночном капилляре радиуса r 2 .
Определим, как изменится подъём воды в рассмотренном нами случае по сравнению с приведённым на рис. 1. Для этого, вычитая из (17) соотношение (4) получим:
r 2 ( r 2 1
Н об - H = h 2 r 1 / r 2 + h” - h 2 - h 1 — г = h 2 ( r 1 / r 2 - 1 ) , (18)
r2 I r2 J откуда следует, что с увеличением разницы в радиусах r1 и r2 увеличивается и высота подъёма воды в капилляре (рис. 7) по сравнению с капилляром рис. 2. Так, если r1 = 2r2, то из (18) следует, что
H o 6 - H = h 2 .
То есть в рассмотренном нами случае высота подъёма воды увеличилась вдвое по сравнению с капилляром, показанным на рис. 1, и уж тем более — по сравнению с одиночным капилляром радиуса r 1 . При r 1 < r 2 правая часть (18) становится отрицательной, следовательно, H об < H . При r 1 = r 2 разность высот в (18) равна нулю. Полученный результат показывает, что наличие перфорированной поперечной перегородки в капилляре большого радиуса, при прочих равных условиях может привести к увеличению высоты подъёма воды в нём и, следовательно, к увеличению её объёма в капилляре.
Если в перфорационной пластинке имеется несколько сквозных отверстий малого радиуса, то подъём воды в таком капилляре может возрасти по сравнению с капилляром, рассмотренным выше. К такому же результату может привести и несоосное расположение отверстий в перфорационных пластинках.
Трахеи ксилемы не обязательно расположены вертикально и могут при своём прохождении в стволе изгибаться. Рассмотрим, как будет продвигаться вода в капилляре радиуса r 1 , изображённом на рис. 8, а, в котором часть капилляра длиной l наклонена к горизонту под углом в . Обозначим высоту выступающей над водой части капилляра до его наклонённой части через h , высоту продвижения воды в вертикальной части после наклонного участка через x , а общую высоту подъёма воды в капилляре через H . Уравнение, описывающее подъём воды в таком капилляре, может быть записано в следующем виде:
nr^cgh + n r 12 leg sine + п rcgx = 2 n r 1 y cos a (19)
откуда x = (2п r1 y cos a)/ (nr12cg) - (nr12lcg sinp) / (nr12cg) - (nrcgh) /(nr12cg) = h1 -1 sinp - h (20)
Полагая x = 0, можно получить максимально возможную длину l макс наклонного участка капилляра при заданном h :
1макс =(hl - h) /sine(21)
или, задавая l, определить максимально возможную высоту h макс :
hMakc = hl -1sinp.(22)
Из (21) и (22) следует, что при изменении β от 0° до 90° величина l макс изменяется соответственно от ∞ до h 1 – h , а h макс — от h 1 до h 1 – l .
Величина общего продвижения L воды в капилляре будет равна:
L = h +1 + x = h +1 + h1 -1 sine - h = h1 +1 (1 - sine),(23)
а высота подъёма воды H в капилляре с учётом (21) и (22) будет равна:
H = h +1 sinp + x = h +1 sinp + h1 -1 sinp - h = h1.(24)
Из (23) и (24) следует, что общая высота подъёма воды H в таком капилляре не зависит от угла наклона его средней части и всегда равна высоте подъёма воды в вертикальном капилляре того же радиуса, а величина продвижения воды L в капилляре зависит от радиуса капилляра и угла наклона его средней части.
Так при в = 90°, L = h i , а при в = 0° L = h i + l = H + l (25)
При этом, если величина h 1 определена радиусом капилляра, то величина l ничем не ограничена и может принимать любые значения, но в любом случае H равна h 1 . Отсюда следует вывод, что одна и та же сила поверхностного натяжения воды в капилляре заданного радиуса может перемещать объём воды больший, чем в вертикальном капилляре того же радиуса, при наличии в нём участков, параллельных поверхности воды в сосуде.
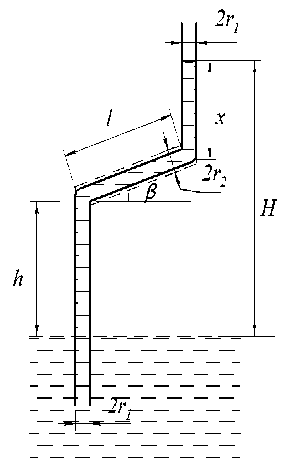
Рис. 8, а. Модель непрямолинейного капилляра
Если наклонная часть капилляра имеет диаметр, не равный диаметрам вертикальных частей капилляра (см. пунктир на рис. 8, а), то уравнение (19) примет вид nr2cgh + nr22leg sine + n r^cgx = 2n-1 y cos a, (26)
откуда r2
x = ( 2nry cos a ) / ( n - 12 cg ) - ( n r 2 2 lcg sin в ) / ( nr2cg ) - ( n- 12 cgh ) / ( n - 12 cg ) = h 1 - ^ l sine - h (27)
r 1
Полагая x = 0 и задавая величины h или l , получим значения l макс и h макс в виде:
U = -^ (h- h)/sine,(28)
r 1
hмакс = hl — -^ l sine,(29)
r 2
а соотношения для L и H примут вид:
( —2
L = h + 1 1 - 2- sine ,
' I -2
,' \ 7
(
H = h + 1 - — l sin0.
r 2
При изменении угла в от 0° до 90° величина 1макс изменяется в пределах от та до ( h 1 - h ) , а hMakC r 1
r 2
от h 1 до h. - l и при r 1 = r 2 совпадают с выражениями (24) и (25). Величина L при этом изме- 1 r 12
I r 2 II r 2
няется в пределах от h + l до h + 1 - l, а H от h 1 до h + 1 - l и при r 1 = r 2 совпадают
I r ) I r )
с (26). Из (30) следует, что при r 1 < r 2 величины L и H уменьшаются, а при r 1 > r 2 увеличиваются по сравнению со случаем r 1 = r 2 . Физически это означает, что одна и та же сила поверхностного натяжения удерживает меньший или больший объём воды. Но при β = 0 величины L и H не зависят от соотношения величин r 1 и r 2 , и в рассмотренном капилляре в горизонтальном направлении может перемещаться любой объём воды под действием любой силы поверхностного натяжения.
Для более сложной капиллярной системы радиуса r 1 , изображённой на рис. 8, б и содержащей m наклонённых под углом β и параллельных друг другу участков длиной l , с расстоянием между ними равным ∆ h , уравнение продвижения воды может быть записано в виде:
пг cgh + 2 ( m - 1 ) п r cgAh + m n r 12 Cg sine + nrcgx = nry y cos a (31) n r 12 cgx = 2 n r 1 y cos a - n r 12 cg ( h + 2 ( m - 1 ) A h + ml sine ) (32)
откуда x = h1 - h - 2 (m -1) Ah - ml sine, H = h + 2(m -1) Ah +l sine + x = h + 2(m -1) Ah + h1 - 2(m -1) Ah - ml sine = = h1 + (1 - m) l sine.
Задавая попарно в (30) величины h, m и l и полагая х = 0, можно получить значения lмакс, hмакс и mмакс в виде lMakC =( h1 - h - 2 (m - 1) Ah ) / m sine, hMakC = h1 - 2 (m - 1)(Ah - l si^) ,
m Makc = ( h 1 - h + 2 A h ) / ( 2 A h - 1 sine ) .
Из (35) следует, что при заданном h l макс и h макс уменьшаются по мере увеличения количества наклонных участков, расстояния между ними (т. е. с увеличением объёма поднимаемой воды) и угла наклона β. По этой же причине уменьшается величина m макс . При m = 1 соотношения (35) преобразуются в (21) и (22). Из (34) следует, что общая высота подъёма воды в рассматриваемой системе зависит только от количества, длины наклонных частей и их угла наклона β, с увеличением которых высота подъёма воды уменьшается и становится равной нулю при h 1 = ( 1 - m ) l sine.
При в = 90° (рис. 8, в) H = h 1 + ( 1 - m ) l. При m = 1 вода поднимается до h 1 — высоты её подъёма в одиночном капилляре радиуса r 1 . При m > 1 высота подъёма воды уменьшается и при l > ( h 1 - h ) / m продвижение воды в верхний вертикальный капилляр не происходит. При в = 0° высота подъёма воды в рассматриваемой системе (рис. 8, г) не зависит от количества горизонтальных частей ( m ) и всегда равна h 1 .
При этом независимо от количества горизонтальных участков не требуется приложения дополнительных сил, а подъём воды обеспечивает только сила поверхностного натяжения в одиночном вертикальном капилляре верхнего уровня. Легко показать, как это было сделано выше, что радиусы капилляров горизонтальной части такой системы не влияют на высоту подъёма воды. Увеличение или уменьшение этих радиусов приводит соответственно к уменьшению или к увеличению сопротивления передвижению воды.
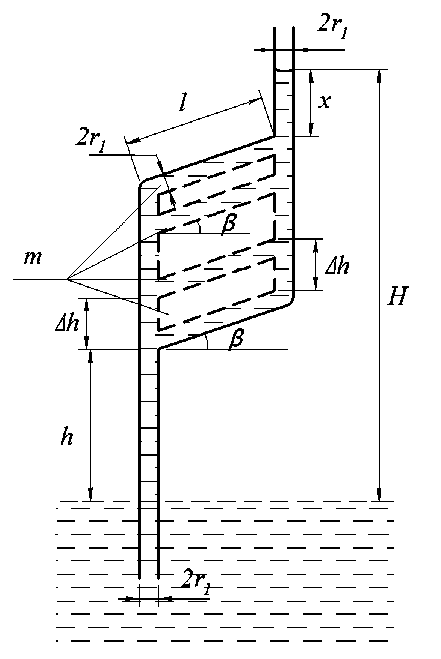
Рис. 8, б. Модель капиллярной системы с m наклонными участками
Полученный результат полностью согласуется с реальным процессом передачи воды от трахеиды к трахеиде, описанным в [2—4]: процесс передачи воды между многочисленными строго соосными порами трахеид различных вертикальных ярусов происходит строго горизонтально, а малые проходные сечения пор компенсируются их количеством. При наличии данных о скорости продвижения воды через реальные поры трахеид разных диаметров (которыми мы не располагаем) можно, подбирая радиусы горизонтальных капилляров с учётом их сопротивления движению воды, численно смоделировать процесс передачи воды в трахеидах.
Рассмотрим далее, как будет продвигаться вода в капиллярной структуре, изображённой на рис. 9. Примем радиус погружённого в воду одного капилляра и горизонтальной части равными r 1 , высоту его над поверхностью воды до горизонтальной части равной h , а радиусы n капилляров над горизонтальной частью равными r 2. Тогда уравнение подъёма воды в каждом из капилляров может быть записано в виде
П nrcgh + n r 2 2 lcgx = 2 n r 2 y cos a , (36)
и решением его будет:
, 1 f r? V x = h2 -1 Ш h, (37)
n V r 2 )
величина hкр, при которой подъёма воды в верхних капиллярах не происходит (x = 0), определится из соотношения f л2)
h KP = nh 21~^\, (38)
V r i )
а количество капилляров при этом
V
П кр = h / h 2
V
г 2
2 ))
.
Высота подъёма воды в такой капиллярной структуре равна
H = h + x = h + h 2 —
1 ( Г 2)
n V T? ) h = h 2 + 1
—
1 (£ n V r 2 2
h .
Из (40) следует, что Н при выполнении условия h < h кр не зависит от взаимного расположения капилляров верхнего ряда, а определяется только их количеством и соотношением радиусов капилляров под и над горизонтальной его частью. При этом, если n ^ж , то H ^ h 2 + h , физический смысл этого в том, что весь вес жидкости в капилляре высотой h поддерживается большим количеством капилляров верхнего уровня. При r 1 = r 2 H = h +| 1 — — | h , то есть с увеличением 2 V n )
количества капилляров высота подъёма воды в системе стремится к величине h + h 2 . Изменение соотношения радиусов капилляров может привести как к увеличению, так и к уменьшению высоты подъёма воды.
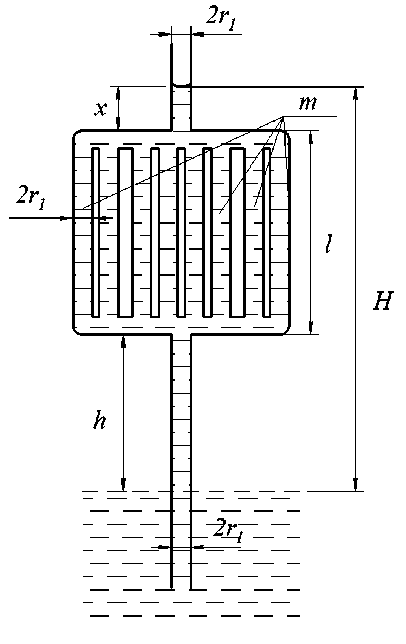
Рис. 8, в. Модель капиллярной системы с m участками при β = 90
В рассмотренном нами случае через один капилляр нижнего уровня вода заполняла всю капиллярную систему. И чем больше количество капилляров во втором уровне, тем медленнее происходит заполнение системы водой. Кроме того, такая система ограничивает имеющееся множество степеней свободы капилляров второго уровня наличием одного капилляра в первом уровне. И любые изменения в капилляре нижнего уровня (например, закупорка или деформация) могут привести к невозможности поступления воды в систему.
Иначе обстоит дело, когда к горизонтальному участку рассмотренной системы в нижнем уровне подводит воду не один, а q (см. пунктиры на рис. 9) капилляров. В этом случае уравнение (36) может быть записано в виде:
П nr^cgh + пГСдх = 2 n r 2 y cos a ,
откуда x = h2 —
g I r 2 )
1 h , n V r J
h -P = gh 2
r 22
r 12
; П - h . / h
V
r 2
r D
.
Величина H для этой системы может быть определена из уравнения
h = h 2 + 1
—
2 g I r_ n V r 2
h .
Из (44) следует, что с увеличением g от 1 до n величина H ^ h 2 , а при увеличении n от 1 до та H ^ h 2 + h . Изменение же соотношения радиусов капилляров верхнего и нижнего уровней также приводит к увеличению или уменьшению Н . Но при r 1 = r 2 и g = n высота подъёма воды в капиллярах равна высоте подъёма воды в одиночном вертикальном капилляре того же радиуса. В случае g > n r 1 = r 2 высота подъёма воды будет уменьшаться и при g и n = const зависит только от соотношения радиусов верхнего и нижнего уровней: по мере увеличения r 1 Н будет уменьшаться до полного прекращения подъёма воды в капиллярах верхнего уровня. При одновременном изменении количества капилляров и их радиусов в обоих уровнях условием максимально возможного подъёма воды будет стремление к нулю второго слагаемого в скобках в (44), что возможно либо при увеличении количества капилляров второго уровня и (или) их радиуса, либо при уменьшении количества капилляров нижнего уровня и (или) их радиуса.
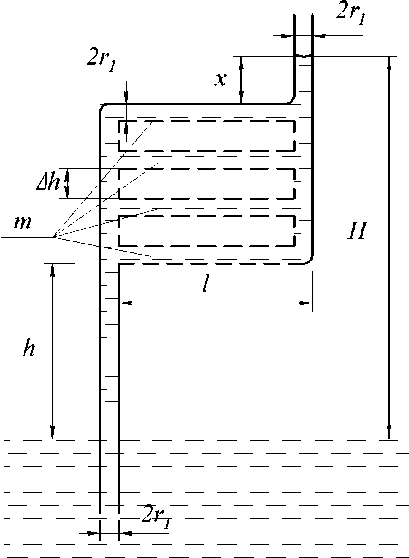
Рис. 8, г. Модель капиллярной системы с m участками при β = 0°
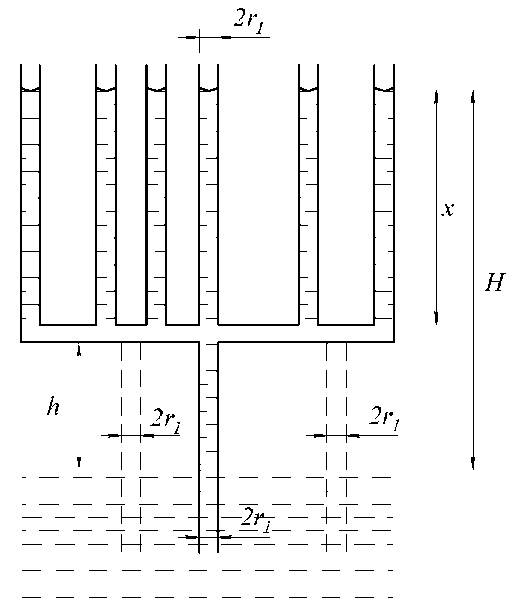
Рис. 9. Модель незамкнутой системы капилляров равного диаметра
В случае n □ q (при прочих равных условиях) капиллярная система имеет значительно больше степеней свободы. Так, любые изменения в одном или в нескольких капиллярах каждого уровня приведут лишь к перераспределению воды в системе. То есть вода получает свободу перемещения в системе в любом направлении, когда выполняется условие:
qr 1 2 ≤ qr 22 (45)
Рассмотрение модели двухуровневой капиллярной системы показало, что с увеличением количества капилляров второго уровня подъём воды в системе увеличивается. Это будет выполняться и для последующих, третьего и более высоких уровней, каждый из которых имеет началом капилляры предыдущего уровня, и приведёт к увеличению подъёма воды в капиллярной системе при условии, что для каждого последующего уровня по отношению к предыдущему выполняется условие (45), которое в общем случае примет вид:
∑ q i r i 2 ≤ ∑ n i r i 2 + 1 (46)
Умножая обе части (46) на π получим
∑ qi π ri 2 ≤ ∑ ni π ri 2 + 1 . (47)
Физический смысл последнего соотношения состоит в том, что для подъёма воды в многоярусной капиллярной системе необходимо, чтобы суммарная площадь капилляров каждого последующего уровня была не меньше суммарной площади капилляров предыдущего уровня. При этом увеличивается возможность свободного перемещения воды в системе. Согласно [4] по высоте ствола число сосудов и площадь их сечения возрастают по направлению от комля к вершине. Учитывая, что кроме сосудов и трахеид ствола в водопроводящую систему растения входит ещё и разветвлённая сосудистая система ветвей разных уровней и сосудистая система листьев этих уровней, можно полагать постоянство выполнения в растении условия (47) и, следовательно, говорить о высокой степени подвижности воды в растении.
Представим, что на рис. 9 капилляры верхнего и нижнего уровней почти примыкают друг к другу. В этом случае коротенькие отрезки горизонтальных капилляров между вертикальными — упрощённая модель порового сообщения между сосудами. Учитывая это и полученные нами выше формулы (17) и (18), можно утверждать, что наличие в сосудах поперечных перфорированных пластин предполагает возможность подъёма воды в сосудах ксилемы на большую высоту (по сравнению со случаем отсутствия таких пластин), обеспечивая при этом построение проводящих сосудов ксилемы большой протяжённости.
Из физиологии растений и экспериментальных исследований [4] известно, что у древесных лиственных пород сосудистая система ксилемы устроена по-разному. У одних она выглядит как кольцо крупных сосудов (аналогично рис. 9, но расположенных в виде кольца) в ранней зоне годичного слоя и как пучки мелких сосудов в зоне позднего годичного слоя (рис. 10) и носит название кольцесосудистой. У других сосуды ксилемы внутри заболони не образуют пучка и кольца, а более или менее равномерно распределены по всей площади заболони, и такая ксилема называется рассеянно-сосудистой и в проведении воды участвуют сосуды совместно с трахеидами (трахеально-сосудистая система). Через поровое взаимодействие сосуды и трахеиды могут образовывать горизонтальные пути прохождения воды в ксилеме. Кроме ксилемы вода в горизонтальном направлении перпендикулярно оси ствола может передаваться по другим тканям растения. Такими тканями в растущем дереве являются сердцевинные лучи, осуществляющие перенос питательных веществ и воды от периферии ствола к его сердцевине (см. [4], рис. 1.10, а, поз. 3).
Количество сердцевинных лучей в ткани дерева велико и доходит до 15000 на 1 см2 на тангенциальном срезе отдельных пород. Наибольшее количество сердцевинных лучей находится в нижней части ствола и уменьшается к кроне, а их объём у лиственных растений может достигать 15 % общего объёма древесины [4]. Наличие в стволе горизонтально проводящих воду тканей и их контактов с проводящими элементами ксилемы также подтверждает соответствие рассмотренной нами модели действительности.
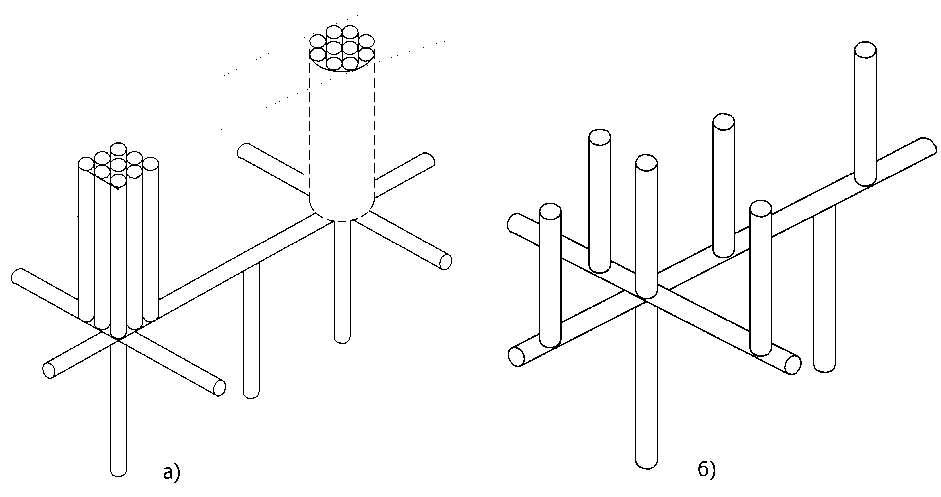
Рис. 10. Схема кольцесосудистой (а) и трахеально-сосудистой (б) систем расположения капилляров
Выводы. Из практики известно, что полное удаление значительной части заболони с одной стороны ствола не приводит к гибели дерева. Проводящие ткани древесины продолжают функционировать, и со временем, дерево восстанавливает нарушенные функции. Если удалить полностью часть заболони параллельно с обеих сторон ствола, то дерево неизбежно гибнет. Объяснить это можно, исходя из модели строения проводящей ткани заболони (сосудов разных типов ксилем), как условно показано на рис. 10. При одностороннем удалении части заболони восстановление возможно, если сосудистая система ксилемы кроме восходящей составляющей потока воды имеет и горизонтальную составляющую, объединяющую сосудистую систему в единое целое. Тогда в сосудистой системе растения произойдёт лишь перераспределение движения воды и ткани, лежащие выше удалённой части заболони не пострадают благодаря наличию горизонтальной составляющей водного потока. А наличие воды в горизонтальной части проводящей системы, как было показано выше, не влияет на продвижение воды в капиллярах и не требует дополнительных сил для подъёма воды. Измениться при этом может только скорость подъёма воды в сосудистой системе дерева. При двустороннем удалении части заболони количество (q) подводящих снизу сосудов уменьшается и согласно (43) величина hкр становится столь малой, что достаточного поступления воды в растение не происходит, и это приводит к его гибели. Для полноты картины необходимо помнить о нарушении процесса образования питательных веществ, нисходящего тока веществ по флоэме и связанного с ним обмена веществ в растении.
Список литературы Капиллярная модель древесных стволов
- Вернигоров, Ю. М. Математическое моделирование распределения жидкости в ветвящихся капиллярных системах/Ю. М. Вернигоров, И. А. Кипнис//Вестник Донского гос. техн. ун-та. -2010. -Т. 10. -№ 8 (51). -С. 1195-1206.
- Лотова, Л. И. Ботаника. Морфология и анатомия высших растений/Л. И. Лотова; изд. 4-е, доп. -Москва: Книжный дом «ЛИБРОКОМ», 2010. -512 с.
- Тимонин, А. К. Ботаника. Высшие растения/А. К. Тимонин -Москва: Издательский центр «Академия», 2007. -Т. 3. -349 с.
- Уголёв, Б. Н. Древесиноведение и лесное товароведение/Б. Н. Уголёв. -Москва: Издательский центр «Академия», 2010. -272 с.
- Жиренко, Н. Г. Изучение сокодвижения в стволе дуба черешчатого термоэлектрическим методом/Н. Г. Жиренко//Лесоведение. -1994. -№ 6. -С. 46-52.


