Карта Птолемея и античные Периплы

* Работа выполнена при финансовой поддержке РГНФ (проект 15-01-00005 «Внутренние структуры карты Птолемея»; URL: .

Антиковедение – дисциплина очень старая, поэтому шанс открыть в зоне её ответственности нечто новое или сделать что-то, чего ещё никто не делал, с течением времени гиперболически стремится к нулю. Тем более удивительны те редкие случаи, когда это всё же удаётся. Так, например, до сего дня, как ни странно, ещё никто и никогда не пробовал сопоставить с картой

ΣΧΟΛΗ Vol. 10. 2 (2016)

Птолемея сведения античных периплов о протяжённости береговой линии.1 Между тем, как будет показано ниже, уже в самом первом приближении такое сопоставление даёт весьма впечатляющие и в определённом смысле неожиданные результаты, которые позволяют сделать ряд далеко идущих выводов как об истории создания карты Птолемея, так и о развитии античной географии в целом.

Периплы в структуре карты Птолемея

Карта Птолемея,2 по всей видимости, изначально строилась на основе довольно грубого геометрического каркаса, унаследованного им от своих предшественников и определявшего её общие очертания и положение ключевых пунктов. Этот каркас складывался из ряда независимых элементов, в числе которых могут быть названы четыре основные категории сведений: (1) сетка ключевых широт и долгот – так называемых «климатов» и «часовых поясов», (2) геометризированная схема очертаний основных регионов, (3) периплы или описания побережий, и (4) итинера-рии или описания дорог.3

Система климатов (κλίµατα) и часовых поясов (ὡριαῖα) описывала географические координаты в единицах времени: широту – как продолжительность самого долгого светового дня, долготу – как разницу в местном времени суток. На этом принципе строились списки широт, следующих через интервалы в 1 час, % или % часа (например - 12%, 12%, 13 и т. д. часов), и долгот, идущих через интервалы в 1 час, % или % часа (1 час разницы в местном времени соответствует интервалу в 15° долготы), для каждой из которых перечислялись связанные с ней пункты. Именно такая система составляла основу карты Марина Тирского, непосредственного предшественника Птолемея и главного источника сведений для его «Географии». При этом, если часовые пояса для выражения долготы впервые стал использовать именно Марин, то система климатов была, по сути, главным инстру-

Д. А. Щеглов / ΣΧΟΛΗ Vol. 10. 2 (2016) 673 ментом для построения математически строгой карты мира в арсенале всей античной географии от Эратосфена и до Птолемея.4

Под «геометризированной схемой» следует понимать, прежде всего, способ описания пространства аналогичный системе «сфрагид» Эратосфена5 или «провинций» у Марка Випсания Агриппы.6 Оба эти автора делили известный мир на регионы, которые могли быть условно представлены в виде четырёхугольников с указанием их размеров и границ по сторонам света.7 Очертания ряда сфрагид Эратосфена и регионов Агриппы отчётливо читаются на карте Птолемея.8

Периплы и итинерарии описывали линейную последовательность географических пунктов вдоль побережья и внутри материка, соответственно.9 Важная в контексте данной статьи особенность системы Эратосфена, а также во многом и работы Агриппы, заключалась в том, что исходные оценки расстояний в них часто, если не сказать «как правило», округлялись и сокращались с тем, чтобы свести их к расстоянию по прямой,10 тогда как в обычных периплах и итинерариях они указывались с учётом всех изгибов пути.

Из всего перечисленного именно перипл служил в античную эпоху основной моделью описания пространства. Многие географические сочинения античности – Артемидора, Страбона, Помпония Мелы, III–VI книги Плиния, Дионисия Периэгета и др., – хотя отнюдь не ограничивались описанием побережья, строились по модели перипла. Сам Птолемей прямо отмечает ( Geogr . 1.18.6), что наиболее точные и надёжные из имеющихся сведений – это именно описания побережий. Естественно предположить, что во многих отношениях именно периплы послужили ему наиболее важным опорным элементом для построения карты.

До нас дошло всего несколько «подробных» периплов эпохи античности: периплы Понта Эвксинского Мениппа Пергамского и Флавия Арриана, послужившие основой для более полного перипла Псевдо-Арриана,11 а также «Стадиасм Великого моря».12 Зато благодаря, главным образом, двум источникам, «Географическому очерку» Агафемера13 и III–VI книгам «Естественной истории» Плиния Старшего,14 мы располагаем многочисленными ссылками на данные разных географов о суммарной протяжённости береговой линии с учётом её изгибов.15 Эти данные охватывают большую часть известного античным географам мира: всё Средиземноморье вместе с атлантическим побережьем Испании, Галлии и западной Африки, Красное море, Аравийский полуостров, Персидский залив и Каспийское море. Крайне любопытно было бы сравнить эти данные с картой Птолемея. Но предварительно необходимо сказать о методе такого сравнения.

Специфика карты Птолемея

Карта Птолемея – первая в истории карта, представленная полностью «в цифровом формате», т. е. состоящая почти исключительно из списков географических пунктов с координатами их широты и долготы.16 О том, как Птолемей работал со своими источниками и как вычислял координаты, нам не известно почти ничего. Поэтому наиболее очевидный способ прочтения карты Птолемея – это считать её тем, чем она и является по сути, – каталогом сферических координат. Расстояние между двумя пунктами, заданными такими координатами, рассчитывается по правилам сферической тригонометрии, а расстояние, последовательно связывающее множество таких точек, – как сумма отрезков между ними.17 Птолемей, разумеется, не располагал тригонометрическими формулами в современном их виде, однако теоремы Менелая, которые он использовал для решения аналогичных задач, по сути им эквивалентны.18 Трудно представить, тем не менее, чтобы Птолемей специально вычислял координаты для каждой из шести тысяч точек на своей карте. Более правдоподобно допустить, что вычисления он производил только для наиболее важных пунктов, тогда как для определения положения остальных использовал более простые способы, например, теорему Пифагора и/или обыкновенную линейку.

Координаты Птолемей указывает с точностью (в значении precision) до 5′. Однако это не должно вводить в заблуждение относительно точности (в значении accuracy) его источников и его методов работы с ними. Точность координат Птолемея отчётливо коррелирует с плотностью заполнения и степенью детализации карты: в наиболее «разреженных» областях периферии (таких, как Азиатская Скифия или Внутренняя Ливия) процент координат, выраженных в целых градусах, максимален, а по мере приближения к Средиземноморью малые доли градуса используются всё чаще. Иными словами, Птолемей указывал точные координаты не потому, что располагал точными сведениями, а для того, чтобы поместить много точек на ограниченном пространстве. Статистический анализ частоты использования Птолемеем различных долей градуса в координатах показывает, что он был склонен округлять все значения.19 Образно говоря, карта Птолемея имела «низкое разрешение»: она хорошо передавала общие очертания больших объектов, но в мелких деталях допускала значительные искажения, которые усиливались по мере удалёния от основных центров Средиземноморья. По этой причине для сравнения карты Птолемея с данными других источников о расстояниях, есть смысл использовать только относительно большие расстояния, а также помнить, что в силу особенностей карты точных совпадений с другими источниками от неё ожидать не стоит.

Текст «Географии» Птолемея дошёл до нас в двух редакциях, которые принято обозначать сиглами В и Q. 20 Обе они восходят к античной эпохе. Редакция В считается ранней и, вероятно, более аутентичной, однако представлена она почти исключительно одной единственной рукописью Vaticanus Graecus 191 конца XIII века, которая к тому же приводит координаты только для западной половины карты (для Европы, Африки, Малой Азии и части Закавказья) и содержит много ошибок. Редакция Q, судя по многим признакам, вторична по отношению к В, но представлена целым рядом рукописей значительно лучшего качества (конца XIII – начала XIV вв.).²¹ Ввиду этих обстоятельств для сопоставления с данными периплов следует использовать обе редакции, но предпочтение отдавать версии В. Все координаты карты Птолемея, используемые для расчётов в данной статье, основаны на электронной базе данных, приложенной к новейшему изданию «Географии».²² Построенные на основе этой базы данных ГИС-карты находятся в открытом доступе на странице проекта «Внутренние структуры карты Птолемея».²³

Сравнение данных периплов с картой Птолемея

Обратимся к источникам. Прежде всего, Артемидор24 и Исидор25 указывают суммарную протяжённость берегов Средиземноморья (рис. 1): Европы от Столпов Геракла (у Птолемея это – Кальпе, Гибралтар) до устья Танаиса (Дон), Азии от Танаиса до Канобского устья Нила и Ливии от Канобского устья до Тингиса (Танжер). Для Европы оба географа дают одно и то же значение - 69 709 стадиев,26 что на 1469 стадиев или всего на 2% меньше значения, которое даёт Птолемей (В) - 71178 стадиев. Для Азии Артемидор и Исидор указывают 40 111 стадиев,27 что всего на 1049 стадиев меньше значения, которое даёт Птолемей – 41 160.28 Тимосфен Родосский29 указывает протяжённость берегов Азии от Канобского устья до устья Понта (у Птолемея это значит – до Халкедона) – 2638 m.p. = 21 104 стадия,30 что на 743 стадия меньше значения, которое даёт Птолемей по версии В - 21 847.31

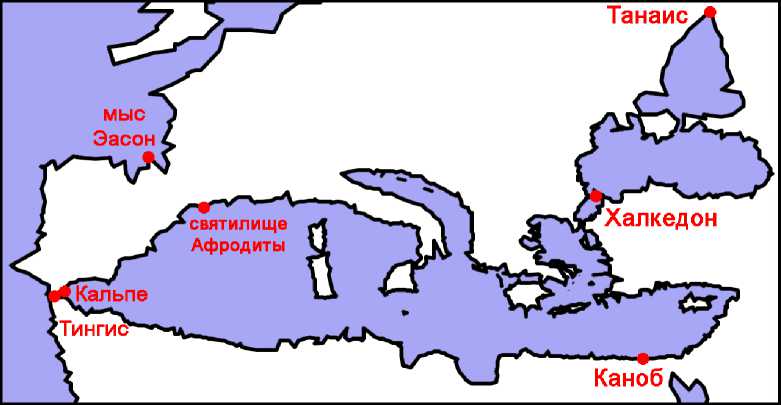
Рис. 1. Средиземное море на карте Птолемея (по версии Ξ) .

Сравнивая приведённые значения для Европы и Азии, важно иметь в виду, что Артемидор и вслед за ним большинство других авторов оценивали окружность Меотиды в 9000 стадиев, тогда как Птолемей предположительно использовал оценку 11 248 стадиев (см. ниже). Если это так, тогда из 1500 стадиев общего расхождения между их значениями для побережья Европы, по меньшей мере, 1000 приходилась на Меотиду, а расхождение между значениями для Азии может быть объяснено различными оценками размеров Меотиды полностью.

Для побережья Ливии от Тингиса до Каноба (Рис. 1) значения заметно расходятся: Артемидор даёт 29 252 стадия,32 Исидор – 3697 m.p. = 29 576 стадиев,33 Маркиан Гераклейский (возможно, по данным Артемидора) – 30 280 стади-ев,34 Плиний приводит, по его собственному выражению, «среднее из всего разнообразия значений» – 3798 m.p. = 30 384 стадия35 – из чего можно заклю- чить, что ему были известны и ещё большие оценки. Данные Птолемея на 1052,6 стадия превышает «среднее значение» Плиния – 31 436,6 стадиев.

Эратосфен и Артемидор указывают окружность Персидского залива (не считая пролив в 400 стадиев, или по другим оценкам 40 или 32 стадия),36 а Артемидор указывает также окружность Каспийского моря (не ясно, включая пролив в 1000 стадиев или нет), в обоих случаях – по 20 000 стадиев.37 При этом, согласно Эратосфену, побережья Персидского залива от мыса Гармозы в Кармании до устьев Евфрата и оттуда до мыса Мак в Аравии составляют по 10 000 стадиев.38 Карта Птолемея даёт для Каспийского моря 20 350 стадиев, а для Персидского залива от Гармозов до восточного устья Тигра – 10 368, а оттуда до Мак – 10 412 (Рис. 2).39

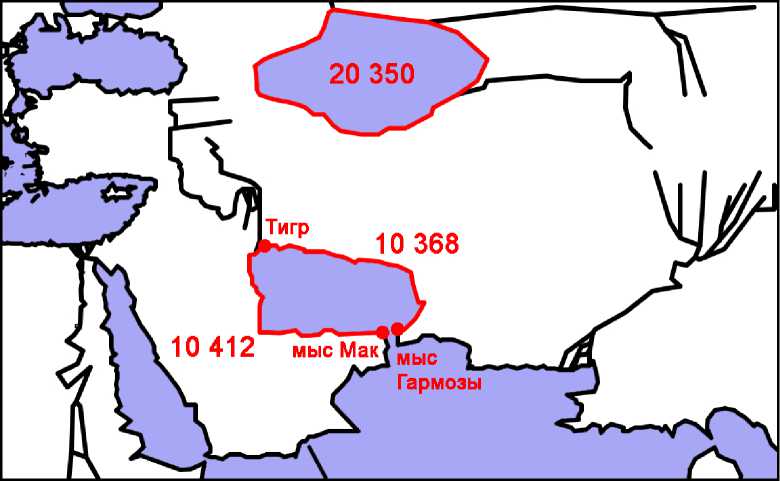
Рис. 2. Каспийское море и Персидский залив на карте Птолемея (версия Ω) .

Плиний указывает окружность Аравийского полуострова от Эланитского залива до Харакса (упоминание которого позволяет предположить, что источником был Исидор) – 4765 m.p. = 38 120 стадиев,40 что всего на 225 стадиев больше значения, которое даёт Птолемей по версии Ω – 37 895.

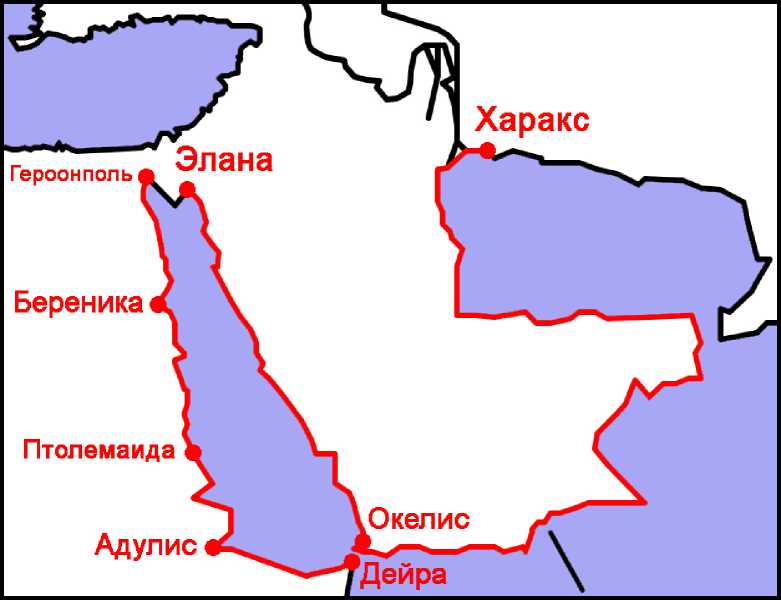
Рис. 3. Береговая линия Аравии от Эланы до Харакса и Африки от Героонполя до Дейры .

Многие античные авторы приводят аналогичные данные для отдельных частей Средиземноморья. Так, Плиний даёт две оценки периметра Испании от атлантического выступа Пиренеев до средиземноморского (у Птолемея – от мыса Эассон до святилища Афродиты), – 2924 m.p. = 23 392 стадиев и 2600 m.p. = 20 800 стадиев.41 Вторая из этих оценок всего на 368 стадиев больше значения, которое даёт Птолемей по версии Е - 20 432 стадия, или на 445 стадиев меньше значения по версии Q - 21245,6 стадия.42

Плиний без ссылки на источник43 указывает периметр Италии от устья реки Вар до устья реки Арсий – 2049 m.p. = 16 392 стадиев,44 что всего на 371 стадий меньше значения, которое даёт Птолемей – 16 763.45

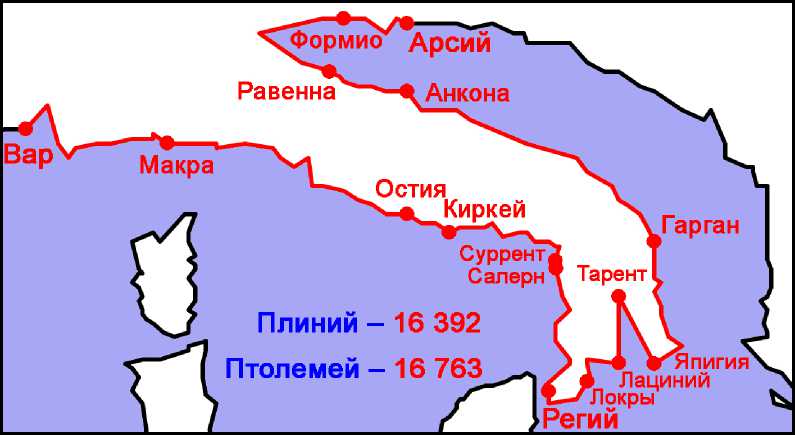
Рис. 4. Береговая линия Италии от Вара до Арсия .

Плиний, предположительно по данным Варрона,46 указывает протяжённость отдельных участков побережья Италии, которые в сумме дают для её южной стороны от устья реки Вар до Регия 890 m.p. = 7120 стадиев,47 что всего на 267 стадиев меньше, чем у Птолемея – 7387.

Тимосфен,48 Посидоний49 и Агриппа50 указывают окружность Сицилии – 4740, 4400 стадиев и 618 m.p. = 4944 стадия, соответственно. Карта Птолемея даёт 4447,3 стадиев по версии Ξ, что практически совпадает с оценкой Посидония, или 4913,3 стадиев по версии Ω,51 что также почти совпадает с оценкой Агриппы.52

Плиний без ссылки на источник указывает окружность «второго залива» Европы между Италией и Иллирией от мыса Лациний до мыса Акрокеравн в Эпире – 1700 m.p. = 13 600 стадиев,53 что всего на 214 стадиев меньше, чем у Птолемея – 13 814.

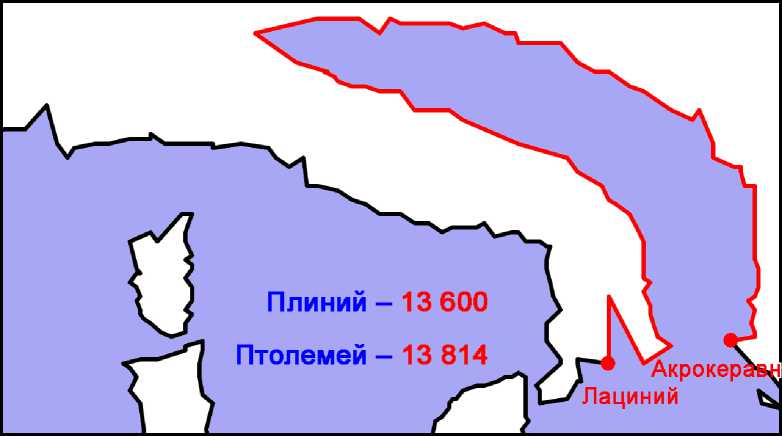
Рис. 5. Береговая линия «второго залива» Европы по определению Плиния .

Плиний без ссылки на источник указывает окружность «третьего залива» Европы от мыса Акрокеравн до Геллеспонта «за вычетом малых заливов» – 1925 m.p. = 15 400 стадиев.54 Поскольку точно не известно, какие именно заливы Плиний относил к числу «малых», а какие нет, полагаться на это свидетельство рискованно. Тем не менее, попробуем в качестве эксперимента измерить на карте Птолемея протяжённость побережья от Акроке-равна до Сеста за вычетом наиболее заметных заливов, упомянутых Плинием (Рис. 6): Амбракийского (между Никополем и Левкой), Коринфского (между мысами Рион и Антирион), Мессенского (между мысами Акрит и Тенар), Лаконского (между мысами Тенар и Малеи), Арголийский (между мысами Малеи и Скиллея), Фермейского, Торонийского и Сингитского (разумеется, выбор именно этих заливов является довольно произвольным). В результате протяжённость береговой линии у Птолемея, составлявшая с учётом всех изгибов 21 013,7 стадия в версии Ξ и 21 499,4 стадия в версии Ω, за вычетом перечисленных заливов составила – 14 985,5 стадия в версии Ξ и 15 773,5 стадия в версии Ω, что согласуется с данными Плиния.

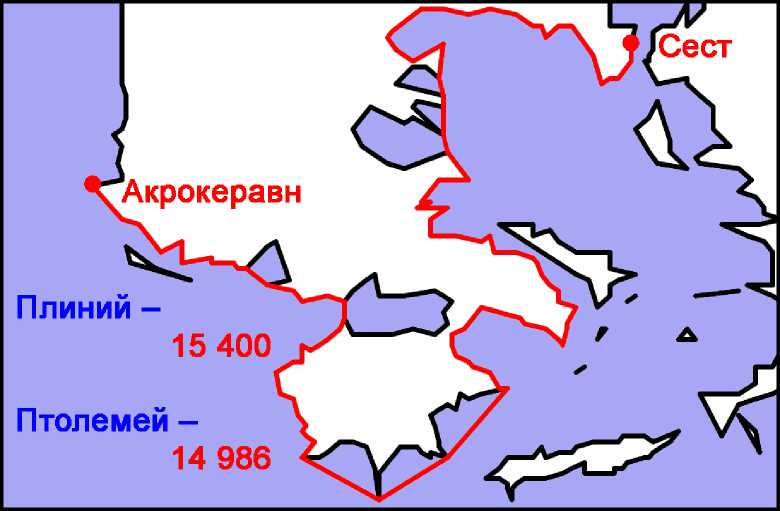
Рис. 6. Береговая линия «третьего залива Европы» согласно Плинию .

Ряд авторов указывают периметр Понта Эвксинского, в частности: Эратосфен – 23 068 стадиев,55 Артемидор – 2919 m.p. = 23 352,56 «Перипл Понта Эвксинского» – 23 577,5,57 Страбон (2.5.22 C125) – 25 000 (очевидно, округлённое значение), что довольно близко к данным Птолемея – 24 078,4 (Ξ) и 24 157 (Ω).58

Для окружности Меотиды источники обычно приводят оценку Артеми-дора – 9000 стадиев,59 однако Плиний (4.78) без ссылки на источник (кроме неопределённого traditur) даёт альтернативную оценку – 1406 m.p. = 11 248 стадиев, что точно совпадает с данными Птолемея по версии Ω.60 Кроме того, Плиний указывает расстояния по прямой через открытое море от Боспора Фракийского до Боспора Киммерийского 500 m.p. = 4000 стадиев (4.77 = Polyb. 34.15.5 Büttner-Wobst) и оттуда до устья Танаиса 375 m.p. = 3000

Д. А. Щеглов / ΣΧΟΛΗ Vol. 10. 2 (2016) 685 стадиев (4.78).61 Наложенные на карту Птолемея, эти расстояния демонстрируют почти идеальное совпадение с её параметрами (Рис. 7).

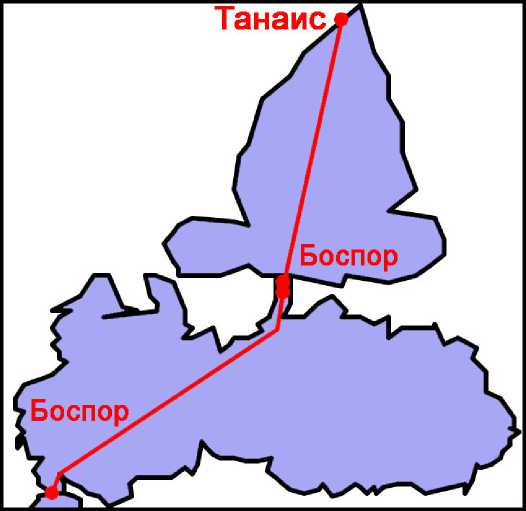
Рис. 7. Расстояния по прямой между двумя Боспорами и устьем Танаиса .

Подведём предварительные итоги. В большинстве рассмотренных примеров речь идёт о побережьях большой протяжённости и крайне сложной конфигурации. При таких условиях между данными периплов и Птолемея трудно ожидать близких совпадений. Тем не менее, такие совпадения оказались настолько многочисленными, что представляются скорее правилом, чем исключением. Все данные по рассмотренным примерам более подробно даны ниже в Таблице 1 и проиллюстрированы диаграммами на рисунках 8 и 9.

Таблица 1. Протяжённость береговой линии по данным периплов и карты Птолемея, согласно версиям Ξ и Ω. Отдельно показывается, насколько данные Ξ и Ω превышают данные периплов, а данные Ω превышают данные Ξ в стадиях и в процентах .

См. Вкладку

.

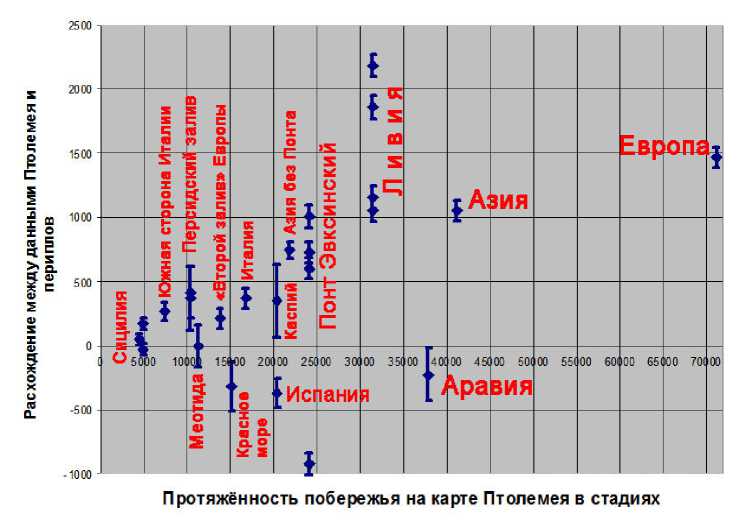
Рис. 8. Завышение расстояний на карте Птолемея относительно данных периплов в стадиях (по оси Y) . В качестве погрешности указывается среднеарифметическое расстояние между двумя пунктами на данном побережье .

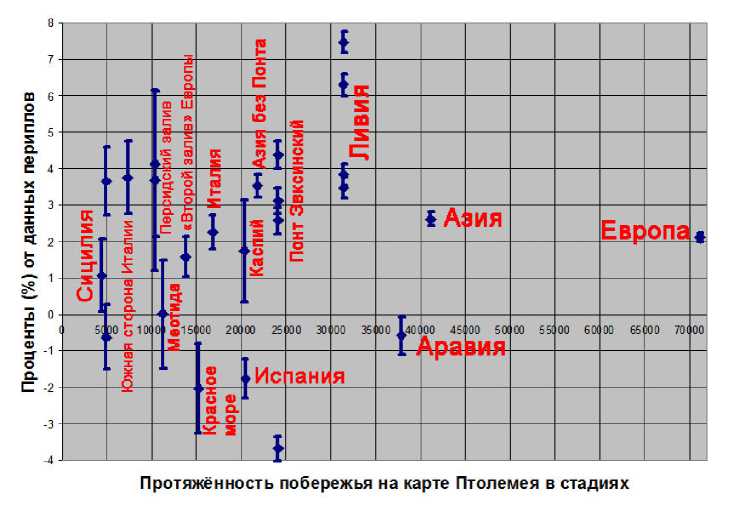
Рис. 9. Завышение расстояний на карте Птолемея относительно данных периплов в процентах от значений, указанных в периплах (по оси Y) . В качестве погрешности указывается среднеарифметическое расстояние между двумя пунктами на данном побережье .

Диаграммы на рисунках 8 и 9 показывают, что в большинстве случаев расхождения между данными периплов и карты Птолемея в редакции Ξ лежат в пределах от +1200 до –800 стадиев или же от +5% до –3% от значений, 62 указанных в периплах.

Как следует оценивать эти цифры? Такие расхождения – это много или мало? Для ответа на этот вопрос сравним их с тем, насколько расходятся между собой два варианта карты самого же Птолемея. Удобным примером для такого сравнения может служить периметр всего Внутреннего моря (Средиземного, Чёрного и Азовского морей): по данным версии Ξ он составляет 143 774,7 стадия, что на 4378,7 стадия больше, чем даёт Исидор – 139 396, но на 3494,2 стадия меньше, чем даёт версии Ω – 147 268,9. Иными словами, суммарное расхождение между Исидором и Ξ на 25% больше, чем между Ξ и Ω, однако величины эти вполне сопоставимы друг с другом. В ряде случаев (побережья Европы в целом, Испании, Италии, «второго залива Европы», Красного моря) расхождения между Ξ и Ω заметно превосходят расхождения между Ξ и периплами (см. Таблицу 1). При этом почти всегда версия Ξ даёт большие расстояния, чем периплы, но меньшие, чем Ω.

Такой характер расхождений легко объясним из общих соображений. Периплы описывают, разумеется, маршрут каботажного плавания, однако при этом они отнюдь не обязательно учитывают все незначительные, но многочисленные изгибы побережья. Неудивительно поэтому, что на карте Птолемея, где эти изгибы отражены, длина побережья с их учётом превосходит расстояния, указанные в периплах. Поскольку Ω является второй редакцией, профиль побережья в ней проработан ещё более детально, чем в редакции Ξ, что дополнительно увеличивает его длину и усиливает расхождение с данными периплов.

62 Разумеется, также можно привести много примеров явных расхождений между данными Птолемея и других источников. Так, побережье Галлии, согласно Агриппе (F 23 = F 40 Klotz = Plin. 4.105), имеет протяжённость 14 000 стадиев, тогда как у Птолемея – всего около 10 000. Побережье Испании от Пиренеев до мыса Магнум (Барбариум у Птолемея), согласно Плинию, занимает 10 000 стадиев, тогда как у Птолемея – всего около 8500. Расстояние от Гадеса (по карте Птолемея правильнее будет считать не от самого Гадеса, а от святилища Геры на побережье) вокруг Священного мыса до мыса Артабров (мыс Нерий у Птолемея), согласно Артемидору (Agathem. 4.16; Plin. 2.242), 7932 стадия, тогда как у Птолемея всего 7032 (Ξ) или 7075 (Ω), что довольно близко, но не достаточно. Окружность Крита, согласно Артемидору (Agathem. 5.26), составляет 4100 стадиев, тогда как у Птолемея – 3802 (Ξ) или 4556 (Ω); варианты изображения Крита у Птолемея см. Данные Артемидора о Кипре, Сардинии и Корсике расходятся с картой Птолемея ещё сильнее. Не составит труда найти ещё большие противоречия между картой Птолемея и теми или иными данными других источников, однако было бы опрометчивым ожидать от них совпадения всегда и во всём.

Ошибка Птолемея в оценке окружности Земли

Сведения, полученные из периплов, неизбежно должны были вступать в противоречие с другими источниками Птолемея, в частности – с данными о широтах. В этом случае противоречия особенно заметны, поскольку в основу своей карты Птолемей положил примерно на 16,8% заниженное значение окружности Земли – 180 000 стадиев = 33 300 км. Вследствие этой ошибки участки побережья, ориентированные с севера на юг и содержащие пункты с астрономически измеренными широтами, оказывались так же сжаты примерно на 17%.

Ещё более любопытный эффект от заниженной оценки окружности Земли наблюдается в тех случаях, когда побережье, протяжённость которого указывается в периплах, состоит из двух частей: одна – ориентированная с севера на юг, другая – с запада на восток. В целом ряде таких случаев первая часть оказывается сжата, что закономерно, а вторая часть – растянута пропорционально первой, что уже требует дополнительного объяснения. Разумно предположить, что такое растяжение было обусловлено стремлением сохранить неизменной суммарную протяжённость всего побережья. Если это объяснение верно, оно даёт нам важный ключ к пониманию методов работы Птолемея.

Описанный эффект пропорционального сжатия/растяжения наиболее ярко наблюдается на трёх примерах: Италии, Каспийского и Красного морей. У Италии южная её часть оказалась зажата между широтами Сицилийского пролива и Неаполя, а средняя часть между Неаполем и Римом пропорционально растянута с запада на восток (Рис. 4). У Каспийского моря вместе с окружностью Земли сократилась его протяжённость с севера на юг, но пропорционально выросла протяжённость с запада на восток (Рис. 2). У Красного моря (его античное название – Аравийский залив) большая часть его африканского побережья, ориентированная с севера на юг, зажата между широтами его северной оконечности и Птолемаиды Охотничьей, а южная часть, поворачивающая на восток до Дейры, – пропорционально растянута (Рис. 3). Ниже эти три примера будут рассмотрены подробнее.

Италия

Продемонстрированное в предыдущем разделе впечатляющее согласие между картой Птолемея и данными периплов в оценках больших расстояний резко контрастирует с тем, какую картину даёт аналогичное сравнение по отдельным коротким отрезкам, из которых эти большие расстояния

Д. А. Щеглов / ΣΧΟΛΗ Vol. 10. 2 (2016) 689 складываются.63 Хорошим примером этого контраста может служить Италия (см. выше Рис. 4). Отдельные отрезки, образующие её периметр согласно Плинию,64 соотносятся с данными Птолемея следующим образом:

Участки побережья	Плиний	Птолемей		Расхождение между данными Плиния и В		Google Map65
		В	п	m.p.	%
р. Вар – р. Макра	211	219,1	214,8	8,1	3,8%	154–182
р. Макра – Тибр (Остия)	284	315,1	350,4	31,1	11%	215–240
Тибр (Остия) – Киркей	50	53,2	53,2	3,2	6,5%	58–61
Киркей – Суррент	78	155,6	224,2	77,6	99,5%	87
Суррент – Салерн	30	26,5	22,3	–3,5	-11,5%	36–37
Салерн – Регий	237	153,7	167,8	–83,3	-35,1%	200–236
Регий – Локры	66	73	71,7	7	10,7%	100
Локры – мыс Лациний	86 или 75	67,4	71,7	–18,6 / –7,6	-21,6% / -10,1%	83–95
Тарент – Япигия	108	88	78,9	–20	-18,5%	90–100
Япигия – Гарган	234	177,3	189,9	–56,7	-24,3%	215–233
Гарган – Анкона	183	335,4	379,6	152,4	83,3%	200–225
Равенна – р. Формио	189	183,9	187,9	–5	-2,7%	155–190

Таблица 2. Сравнение данных Плиния, Птолемея и современной карты о протяжённости отдельных участков побережья Италии (все расстояния указаны в римских милях; 1 миля = 1480 м).

Приведённые данные показывают, что протяжённость побережья от устья Вара до мыса Киркей у Птолемея преувеличена в сравнении с данными Плиния в среднем на 8% (или на 42,5 m.p.), что довольно много, но всё же может быть объяснено тем, что карта Птолемея почти всегда демонстрирует похожее завышение расстояний относительно периплов. Противоположный этому участок адриатического побережья от Равенны до устья Формио согласуется с данными Плиния с высокой точностью. Зато участок от Кир-кея до Суррента у Птолемея растянут ровно вдвое – на 78 m.p., тогда как участок от Салерна до Регия почти так же сжат – на 83 m.p. Участки противоположного побережья, параллельные этим двум, демонстрируют аналогичные искажения: от Япигии до Гаргана - сжат на 24% или на 57 m.p., от Гаргана до

Анконы - растянут на 83% или 152 m.p. Таблица 2 показывает, что столь же резкие сжатия и растяжения имеют место на всех этих участках и в сравнении с современной картой (см. также рис. 10).

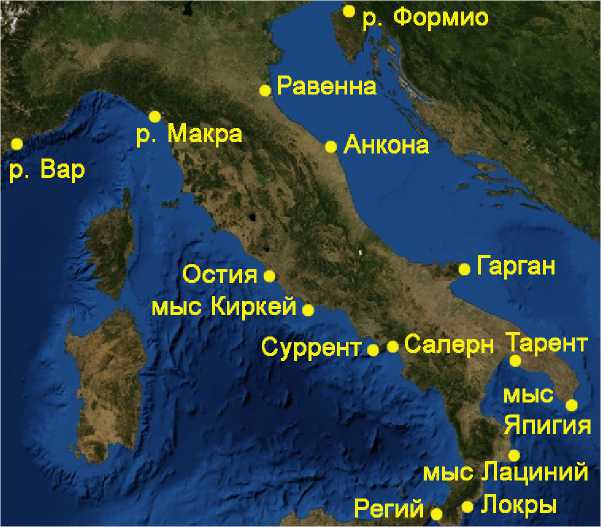
Рис. 10. Упомянутые Плинием пункты побережья Италии на современной карте.

Сжатие южной Италии в направлении с севера на юг легко объясняется, прежде всего, заниженной оценкой окружности Земли, принятой Птолемеем. Так, южная Италия у Птолемея зажата между широтами Неаполя (40° 55' в Е) на севере и Сицилийского пролива (точнее - мыса Пелор на Сицилии, 38° 35' в П) на юге, которые соответствуют климатам с максимальной продолжительностью дня 15 и 14% часов, соответственно. Широты большинства пунктов южной Италии у Птолемея даны довольно точно (например, реальная широта Неаполя - 40° 50'). В частности, интервал между широтами Сур-рента и Регия у Птолемея (2,4°) близок к правильному значению (2,5°), однако из-за неправильной оценки окружности Земли он составляет всего 150 m.p., тогда как при правильной оценке было бы 180 m.p.

Растяжение средней Италии с запада на восток хорошо согласуется с гипотезой о том, что в окончательной версии карты Рим оказался сдвинут примерно на 3° 50' на запад со своего первоначального положения около меридиана 40°, что сказалось на очертаниях всего полуострова.66

Такая ситуация – когда сопоставление множества отдельных коротких расстояний на карте Птолемея и в периплах даёт весьма запутанную и противоречивую картину, однако различные расхождения между ними компенсируют друг друга таким образом, что в итоге достигается почти полное согласие – позволяет сделать важные предположения о методе работы Птолемея. Вероятно, его карта строилась не «от частного к общему» – когда её контуры формировались бы последовательно пункт за пунктом, а «от общего частному» – когда сначала задавались общие очертания и расположение ключевых пунктов, определяемые теми самыми «большими» расстояниями, которые совпадают с данными периплов, а уже потом прорисовывались детали и проставлялись прочие пункты, положение которых подгонялось под общие очертания.

Каспийское море

Совпадение между данными Птолемея и Артемидора о периметре Каспийского моря даёт нам ключ к объяснению его необычной конфигурации на карте Птолемея, а именно – того, почему оно оказалось вытянуто не с севера на юг, а с запада на восток (Рис. 2). Уже исходя из общих соображений, эту аномалию разумно связать с тем, что и вся в целом карта Птолемея демонстрирует такое же сильное растяжение своих очертаний с запада на восток в сравнении с современной картой.67 Это растяжение в значительной мере обусловлено заниженным значением окружности Земли, которое Птолемей положил в основу своей карты. Такой эффект от этой ошибки связан с принципиальной разницей между способами измерения широты и долготы: если широту можно определять путём простейших астрономических измерений, чему греки научились уже к IV в. до н.э., а начиная с Гиппарха (II в. до н. э.) стали выражать широту в градусах, то доступный способ измерения долготы появился только в XVIII веке с изобретением хронометра. Для античного же географа главный способ определения долготы – это был пересчёт расстояний из традиционных линейных единиц измерения (стадиев, миль и т.п.) в угловые (градусы), для чего требовалось знать окружность Земли. По этой причине ошибка в её оценке сказывалась на всех параметрах долготы, но никак не влияла на значениях широт, изначально выраженные в градусах.

Между тем, есть веские основания полагать, что ранняя версия карты Птолемея строилась на основе иной оценки окружности Земли – 252 000

стадиев, которая была предложена Эратосфеном и для античной эпохи может считаться почти общепризнанной. Так, с одной стороны, Пауль Шнабель показал, что даже сам Птолемей использовал эту оценку в «Альмагесте», своём раннем труде.68 С другой стороны, Эрнст Херцфельд, Антонин Вурм и автор этих строк независимо друг от друга показали, что большая область на карте Птолемея была построена на основе данных Эратосфена, в которых расстояния были пересчитаны из стадиев в градусы согласно Эра-тосфеновой же шкале 1° = 700 стадиев.69 Эта область включает в себя, как минимум, всю территорию Азии от Евфрата до Инда, а также, возможно, захватывает Малую Азию и Индию.

Каспийское море примыкает непосредственно к этой «Эратосфеновой» области карты Птолемея и притом даёт основания предполагать, что его ширина, т. е. протяжённость с севера на юг, была также основана на данных Эратосфена, выраженных в градусах по 700 стадиев. Так, Страбон, следуя, вероятно, Эратосфену, определяет меридиональное расстояние между южными оконечностями Каспийского моря и устьем, связывающим его с океаном, на севере как «около» (περὶ) 6000 стадиев (2.1.17 C74), что соответствует 8,57° по Эратосфену. Птолемей даёт близкое значение: широтный интервал между северной (устье Ра, 48° 50') и южной (устье Стратона, 40°) оконечностями Каспийского моря составляет у него 8° 50', что по шкале Эратосфена соответствует 6183% стадиям.70 Примечательно также, что северная оконечность Каспийского моря, так же как и северная сторона Понта Эвксинского, у Птолемея явно привязана к широте устья Борисфена (48%°) - одного из «семи климатов», ключевых широт, определяющих общую структуру его карты и восходящих, вероятно, к Эратосфену.71 На основании этих совпадений можно предположить, что меридиональная протяженность Каспийского моря у Птолемея изначально составляла шесть с небольшим тысяч стадиев, которые были пересчитаны в градусы широты и привязаны к климату Борисфена уже в ранней версии карты, основанной на Эратосфеновой оценке окружности Земли.

Нетрудно заметить далее, что значение 6183% весьма близко к частному от деления 20 000 на число π.72 Если это совпадение не случайно, и если окружность в двадцать и протяжённость с севера на юг в шесть с небольшим тысяч стадиев были теми параметрами, которые определяли очертания Каспийского моря изначально, тогда отсюда математически следует, что в ранней «Эратосфеновой» версии карты, море должно было иметь форму близкую к кругу. После того, как Птолемей перешёл на новое значение окружности Земли, широтная протяжённость Каспийского моря, будучи уже выражена в градусах, осталась неизменной, тогда как его периметр был заново пересчитан в градусы по 500 стадиев, что заставило море вытянуться с запада на восток, придав ему те очертания, какие мы видим на карте Птолемея сегодня.

Правда, в других источниках форма Каспийского моря ни разу не сравнивается с кругом.73 Напротив, источники используют совершенно иные сравнения: серп или рога молодого месяца, или шляпка гриба.74 Однако такой выбор метафор во многом мог определяться тем, что, в отличие от Птолемея, эти источники рассматривали Каспийское море как залив океана. В любом случае круг представляется самой простой и очевидной фигурой, какую можно использовать для описания конфигурации моря или залива, о котором по-настоящему не известно почти ничего.

Красное море

Конфигурация Красного моря у Птолемея в целом определяется широтами четырёх пунктов: Береники, Птолемаиды Охотничьей, Адулиса и Окелиса (Рис. 3).75 Общая протяжённость африканского побережья от Героонполя до Дейры (напротив Окелиса) у Птолемея всего на 2% или на 315 стадиев меньше значения, указанного Артемидором (см. Таблицу 1). Однако если сравнить данные по отдельным участкам побережья, выяснится, что у Птолемея участок от Героонполя до Птолемаиды сжат примерно на 1400 стадиев или на 16%, а участок от Птолемаиды до Дейры - растянут на 1100 стадиев или на 17% относительно данных Артемидора.76 Аналогичные искажения карта Птолемея демонстрирует на этих участках и относительно современной карты (см. Таблицу 3).77

Участки побережья	Эратосфен и Артемидор	Птолемей		Расхождение между данными Артемидора и В		Google Map78
		В	и	стадии	%
Героонполь – Птолемаида	9000	7575	7864	–1424,6	–15,8	8108–8189
Героонполь – Береника	4180	3266	3366	–914,2	–21,9	4324
Береника – Птолемаида	4820	4310	4497	–510,6	–10,6	3784–3865
Птолемаида – Дейра	6500	7609	8211	1109,4	17	4700–4843

Таблица 3. Сравнение данных Артемидора, Эратосфена, Птолемея и современной карты о протяжённости отдельных участков побережья Красного моря (все расстояния указаны в стадиях; 1 стадий = 185 м).

Возможен также совсем иной подход к объяснению конфигурации Красного моря у Птолемея. Если измерить на его карте расстояния по прямой между ключевыми пунктами, согласно Эратосфену и Артемидору (Героон-поль, Береника, Птолемаида, пролив у Дейры, Элана), и пересчитать их в стадии по шкале Эратосфена (1° = 700 стадиев), а не Птолемея (1° = 500 стадиев), то полученные таким образом значения чрезвычайно близко совпадут с расстояниями, которые дают Эратосфен и Артемидор (Таблица 4).

Участки побережья	Эратосфен и Артемидор	Птолемей (В)	Расхождение между данными Эратосфена и Артемидора и В
			стадии	%
Героонполь – Птоле-маида	950079	9470	–30	–0,3
Героонполь – Береника	4180	4212	32	0,76
Береника – Птоле-маида	4820	5299	479	9,9
Птолемаида – мыс Палиндром80	6500	6688	188	2,8
Элана – мыс Палиндром	14 00081	14 191	191	1,37

Таблица 4. Сравнение данных Артемидора, Эратосфена и Птолемея о расстояниях по прямой между ключевыми пунктами на Красном море.

Аналогичным образом с картой Птолемея хорошо согласуется данная Эратосфеном оценка общей протяжённости Аравии с севера на юг: 12 000 стадиев = 17,14° в градусах Эратосфена.82 У Птолемея интервал между широтами Эланы и южного побережья Аравии (примерно 11%°) составляет 17,75° = 12 425 стадиев в градусах Эратосфена, тогда как в градусах Птолемея – всего 8875. Если все эти совпадения не случайны, можно предположить, что общая конфигурация Красного моря на карте Птолемея сложилась ещё на «Эратосфеновском» этапе её формирования и является таким же случайно сохранившимся остатком этой ранней версии, как и, например, значение ширины Каспийского моря, о чём было сказано выше.

Заключение

Главный вывод из проведённого анализа является интуитивно ожидаемым, а именно – что карта Птолемея с большой вероятностью строилась на основе сведений античных периплов, если не тех же самых, какие известны нам по дошедшим источникам, то, по крайней мере, аналогичных им. Неожи- данным же и намного более важным является то, что между картой Птолемея и сведениями периплов обнаруживаются весьма точные совпадения в оценках расстояний, что открывает широкие перспективы для дальнейшего изучения взаимосвязей между ними. Главная проблема на этом пути заключается в том, как примирить между собой, с одной стороны, явное согласие между данными периплов и Птолемея в масштабе больших расстояний, а с другой стороны, столь же явные противоречия между ними в масштабе отдельных мелких деталей. Эту проблему можно сформулировать иначе: в какой степени совпадения между данными периплов и Птолемея могут быть случайными, а в какой – отражающими замысел самого Птолемея? и если они всё же были неслучайны, то за счёт чего они достигались? Иными словами, это вопрос о методе работы Птолемея со своими источниками и о релевантности наших методов изучения его работы. Если же карта Птолемея со всем множеством отражённых на ней разнообразных деталей действительно строилась на основе неких недошедших до нас периплов, это означает, что античные периплы могли содержать намного более подробные и точные сведения о конфигурации побережья, чем допускалось ранее, что может внести существенные коррективы в наши представления об уровне развития античной географии и картографии в целом.