Каскадные процессы и скейлинг в классе моделей МГД турбулентности

Quadratic integrals of motion mostly determine the small scale turbulence structure. In this paper we study a class of shell models of magnetohydrodynamic (MHD) turbulence, which contain three integrals of motion: the total energy, the cross-helicity and the third integral W depending on model’s parameter s. One shows that for 6’< 1 the integral W is a helicity-like integral and the system displays a small scale dynamo effect, characterized by pronounced inertial range with equipartition of magnetic and kinetic energies. In this case the spectral index is close to Kolmogorov's "-5/3”. At e>\ W becomes a positive-defined integral. Then the character of energy transfer processes changes. As s increases, the magnetic energy containing scale moves to small scales. At e >2 the dynamo process becomes impossible and the magnetic field plays a role ofpassive scalar.

Важнейшим признаком развитой турбулентности является наличие широкого интервала масштабов, в котором имеет место каскадный перенос квадратичных величин. Наличие постоянного вдоль всего инерционного интервала спектрального потока энергии определяет характер классической колмогоровской турбулентности. Появление дополнительных квадратичных интегралов движения (величин, сохраняемых в бездисси-пативном пределе) качественно меняет характер каскадных процессов в турбулентности. Так, в двумерной гидродинамике сохраняющейся величиной является энстрофия (средний квадрат завихренности), что делает невозможным перенос энергии в малые масштабы. В результате, в двумерной турбулентности возникают два инерционных интервала: интервал переноса энстрофии в малые масштабы и интервал переноса энергии в большие масштабы.

Турбулентное движение проводящей жидкости описывается уравнениями магнитной гидродинамики (МГД). Запишем их в безразмерном виде для случая несжимаемой жидкости:

d,и + (wV)и = (В^)В-Ч(Р + В2 / 2) + Re 1 Ай, dtB + (uK)B = (BV)u+Rm-' АВ,                             (1)

Vz7 = 0 ,               5? В = 0,

(здесь и - скорость, В - индукция магнитного поля, Р -давление, Re - число Рейнольдса, Rm - магнитное число Рейнольдса) Система (1) в пределе Re,Rm -» ос характеризуется тремя интегралами движения: общей энергией, перекрестной спиральностью и магнитной спиральностью

E = Er. + ЕВ = -|(м2 + B2)dV, Hc^^uB^dV, Нв = ^AB)dlr, где А - векторный потенциал, В = rot А . Из этих трех величин положительно определенной является только энергия, а обе спиральности могут иметь произвольный знак. Отметим, что при переходе к двумерной магнитной гидродинамике два интеграла (энергия и перекрестная спиральность) остаются неизменными, а третий заменяется на квадрат векторного потенциала а = j(A2)dF. Роль интегралов типа спиральности в г каскадных процессах не столь однозначна, как роль положительно определенных интегралов типа энергии и энстрофии. Даже в обычной трехмерной гидродинамической турбулентности, которая помимо энергии сохраняет и спиральность HL, = J(w xotu^dV , v процессы каскадного переноса спиральности и его влияния на каскад энергии по-прежнему вызывают много споров. В МГД-турбулентности ситуация еще более запутана, тем более, что экспериментальный материал по мелкомасштабной МГД-турбулентности практически отсутствует, а прямые численные исследования уравнений (1) с достаточным разрешением только начинаются (например, [1]).

В данной работе сделана попытка определить взаимосвязь законов сохранения и динамики инерционного интервала в системе гидродинамического типа с тремя интегралами движения путем рассмотрения однопараметрического класса каскадных моделей МГД-турбулентности, позволяющих непрерывным образом варьировать третий интеграл движения.

Каскадные модели - это простейшие спектральные модели развитой турбулентности, в которых каждая переменная характеризует амплитуду пульсаций скорости (температуры, магнитного поля и т.д.) внутри целой октавы волновых чисел Представляя собой динамические системы из нескольких десятков уравнений, эти модели, тем не менее, воспроизводят многие достаточно тонкие свойства развитой турбулентности (см., например [2,3]).

Рассмотрим модель МГД-турбулентности, предложенную П Г. Фриком и Д.Д. Соколовым в работе [4]. В отличие от других МГД-моделей [5-7], эта модель в бездиссипативном пределе сохраняет три квадратичные величины, соответствующие всем известным интегралам движения в магнитной гидродинамике. В данной работе модель модифицирована таким образом, что в ней сохранен один управляющий параметр е , отвечающий, в частности, за вид интегралов движения.

Уравнения модели запишем в виде

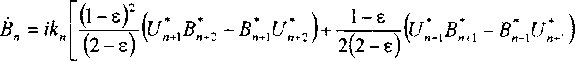
~Вт'к2Вп ,

где U,. и В„ - комплексные переменные, характеризующие соответственно пульсации скорости и магнитного поля в интервале волновых чисел к_п<\к |<А_л+|, к_п = k_tiE. Уравнения (2)-(3) в пределе Re = Rm = оо сохраняют две квадратичные величины

£-Ж!2+18.Г- BeWXty пи являющиеся аналогами общей энергии и перекрестной спиральности Эти величины остаются интегралами движения при любых значениях параметра е. Система (2)-(3) обладает и третьим интегралом движения, который можно записать в виде

^ = y/sign(£--l))"^|SJ2,           Л = log2 | f -11.(4)

Интересно, что при е - 1 меняется тип интеграла движения Для е > 1 интеграл (4) есть величина положительно определенная и при = 5 / 4 является аналогом квадрата векторного потенциала

WY^a^k^\Bn\1(5

Для е < 1 третий интеграл (4) становится знакопеременной величиной и при £■ = 1/2 имеет размерность магнитной спиральности, являясь аналогом соответствующей величины в трехмерной магнитной гидродинамике, w^HB^-xYk;1 \ вп\2.(6)

Отметим, что в работе [4] каскадные уравнения (2)-(3) исследовались для случаев г = 1 / 2 и £ = 5 / 4, соответствующих трех- и двумерной МГД-турбулентности.

Каскадные уравнения (2)-(3) имеют в инерционном интервале стационарные решения вида и„=и»к:. В,=Вйк»                 (7)

Очевидно, что при любых р = а уравнение (3) удовлетворяется автоматически, а уравнение (2) имеет решения, известные для соответствующей гидродинамической модели [2],

«1 = А = -р «2 = А = |log2                   (8)

Первое решение соответствует колмогоровскому спектру Е(к) ~ к "³ и присутствует при любых £ . Можно показать, что в случае Р ^ а стационарных решений для произвольных £ не существует.

движущейся проводящей жидкости. Подчеркнем, что речь идет о так называемом мелкомасштабном динамо, состоящем в генерации магнитного поля на масштабах, принадлежащих инерционному интервалу. Цель численных экспериментов состояла в изучении влияния параметра е, связанного с третьим интегралом движения, на характер каскадных процессов и процесс генерации мелкомасштабного магнитного поля. Рассматривались значения -10 <  е < 10, хотя все примечательные перестройки характера процессов лежат в значительно более узком интервале: -1 <  е < 3 .

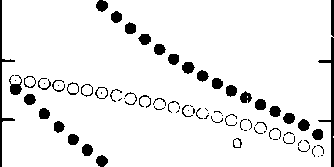
Первый интересный результат состоит в том, что ни при каких значениях параметра £ в системе (2)-(3) не обнаружено устойчивых решений вида (7). Это отличает МГД-систему от чисто гидродинамической каскадной модели, получаемой из (2)-(3) при В_п = 0, в которой для 0 < е < 0,384 колмогоровское решение а = —1/3 устойчиво. МГД-система демонстрирует сложное стохастическое поведение при всех значениях параметра, и под стационарными решениями мы будем подразумевать в дальнейшем решения, получаемые путем осреднения по времени энергии пульсаций (квадрата соответствующей переменной). На рисунке приведены стационарные спектральные распределения кинетической (Ду (и), белые точки) и магнитной (Д_в(и), черные точки) энергий, полученные путем осреднения решений на временах 50 < Z < 75 (время измеряется в характерных временах оборота вихря на большем масштабе). Начало осреднения выбрано так, чтобы оно заведомо превышало время, необходимое для завершения переходных процессов, связанных с конкретными начальными условиями.

На оси £ выделяются две особые точки: £ = 1, в которой меняется тип интеграла движения, и £ = 2, в которой в уравнении (3) возникает особенность, а показатель 2 в интеграле (4) меняет знак.

В области параметра £ < 1 (см. рисунок, a-ж) решения характеризуются устойчивым динамо-процессом, характеризующимся приблизительным равенством магнитной и кинетической энергий практически на всех масштабах. При положительных £ наблюдается ослабление магнитной энергии на самых больших масштабах (и<5), то есть магнитная энергия почти не поступает на масштабы, содержащие максимум кинетической энергии. Тем не менее, равнораспределение магнитной и кинетической энергий сохраняется на протяжении всего инерционного интервала. Наклон спектра в инерционном интервале близок к колмогоровскому, хотя и становится круче при £, приближающихся к единице (см. табл. 1, где приведены показатели степени для спектральных плотностей Д(Л) - к^х, а х = 2а-1 для кинетической и х = 2Д-1 для магнитной энергий).

Качественная перестройка характера решения происходит при е > 1. Блокируются процессы генерации магнитного поля в больших масштабах, причем, чем больше е , тем дальше в мелкие масштабы отодвигается граница интервала, в котором сохраняется равнораспределение кинетической и магнитной энергий (см. рисунок,з-к). Для 1,3 < е < 1,5 в спектре магнитной энергии хорошо выделяются восходящий и нисходящий участки. При е » 1,7 граница этих участков (то есть максимум в спектре) достигает диссипативного интервала (рисунок,л) и при дальнейшем росте £ весь спектр магнитного поля лежит существенно ниже спектра кинетической энергии. Очевидно, что значение е = 1,7 не является выделенным - при изменение вязкости (числа Рейнольдса) будет меняться протяженность инерционного интервала и, соответственно, значение параметра, при котором максимум магнитной энергии достигнет диссипативного масштаба.

0,01

0,01

0,01

0,01

0,01

0,01

0,01

*в*в8оо

8 в®в«®ввв б _-            **®®ево®®8оо

■------------ч

®8®е<

'®®66fiar> г -ввв«вввв8

8”е*ее«,.

ое

т

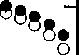
:ф°°оОо

ООООоп

qOOOOoq

'°Ооо

°°ОО°°ооОО|

'°°°°ОО“

^е

ч-

'°°о ио

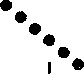
0   5 п10 15

Рис. Энергетические спектры магнитного поля (черные точки) и поля скорости (белые точки) при различных значениях г: а) в = -5; б) £ = -2; в) е = -0,5 ; г) е = 0; д) е = 0,5; е) е - 0,99; ж) е = 1,01; з) е = 1,1; и) в = 1,3 , к) е = 1,5 ; л) е = 1,7; м) 8 = 1,99; н) £■ = 3; о) £-5

Таблица 1

Наклоны спектров энергии поля скорости и магнитного поля (£_г ® Е_с,)

£	2а-1	2/7 — 1
-5,00	-1,716	-1,736
-4,00	-1,742	-1,744
-3,00	-1,672	-1,67
-2,00	-1,622	-1,632
-1,00	-1,676	-1,69
-0,50	-1,678	-1,732
0,00	-1,708	-1,8
0,50	-1,64	-1,634
0,99	-1,74	-1,684
1,01	-1,728	-1,718
1,10	-1,768	-1,706
1,20	-1,738	-1,742
1,25	-1,856	-1,772
1,30	-1,922	-1,838
1,40	-1,996	-1,886
1,50	-2,192	-1,97

Таблица 2

Наклоны спектров энергии поля скорости и магнитного поля ( Е_в « E_i;)

£	2а-1	2/7-1	2А-1	2/?2-1
1,25	-1,722	1,574	0,362	2,444
1,30	-1,814	0,622	0,144	2,102
1,40	-1,648	0,684	-0,354	0,94
1,50	-2,314	-0,306	-0,342	1,628
1,60	-2,28	-0,694	-0,622	1,034
1,70	-2,254	-1,224	-0,858	0,538
1,80	-1,97	-1,328	-1,192	-0,414
1,90	-1,916	-1,612	-1,39	-0,864
1,99	-1,952	-1,924	-1,51	-1,066
2,01	-1,894	-1,924	-1,566	-1,24
2,50	-1,766	-2,936	-2,202	-2,638
3,00	-1,722	-3,374	-2,64	-3,558
4,00	-1,692	-3,172	-3,24	-4,786
5,00	-1,636	-3,684	-3,682	-5,726

Точка е = 2 определяет нижнюю границу области, в которой мелкомасштабный динамо-процесс становится невозможным даже при сколь угодно больших магнитных числах Рейнольдса Рассматривая рисунок,(н-с) и табл. 2, можно видеть, что чем больше s, тем круче становится спектр. В то же время происходит рост энергии крупномасштабного магнитного поля (при 8 » 5 в наибольшем масштабе значения магнитной и кинетической энергии становятся близкими друг другу). Такое поведение связано с тем, что при е > 2 показатель Л в интеграле (4) становится положительным и величина W становится магнитным аналогом обобщенной энстрофии. Последнее означает, что спектральный поток магнитной энергии возможен только в направлении больших масштабов при одновременном переносе W к малым масштабам.

В заключение отметим, что в решениях системы для 8 > 1 в спектре магнитного поля есть участки, в которых его энергия значительно меньше кинетической энергии. Это означает, что обратное влияние магнитного поля на поле скорости слабо и магнитное поле на соответствующих масштабах может рассматриваться как пассивная примесь. Для таких режимов встает вопрос о возможных стационарных решениях В_п = В_ок^, реализующихся при заданном решении для скорости U_п = U_ок“ (то есть требуется найти Д при заданном а). Таких решений три: Р = а , которое существует для любых 8 , и пара решений

1+a + logJff-l! .

А =л А=-(1 + 2« + 1оё21£--ф, (9)

которые возможны только при£ > 1. Из табл. 2 видно, что большинство значений Д, полученных для слабого магнитного поля, не соответствует ни одному из решений (9). Лишь при больших г значения р стремятся к решению Д .

Работа выполнена при поддержке РФФИ (проект 99-01-00362)

• 1.    Mueller W.-C., Biskamp D. Scaling properties of three-dimensional M HD turbulence // Phys. Rev. Lett-2000.-Vol.84.-№.3.-P.475-478.

• 2.    Bifferale L., Lambert A., Lima R., Paladin G. Transition to chaos in a shell model of turbulence/./Physica D.-1995.-Vol. 80.№.1-2.-P. 105-115.

• 3.    Frick P , Dubrulle B., Babiano A. Scaling properties of a class of shell models H Phvs Rev. E.-1995.-Vol.51.-№.6.-P.5582-5593.

• 4.    Frick P., Sokoloff D. Cascade and dynamo action in a shell model of МНЕ* turbulence// Phys. Rev E.-1998.-Vol.57.-№.4.-P.4155-4164.

• 5.    Gloaguen C., Leorat J., Pouquet A., Grappin R A scalar model for MHD turbulence 7 Physica D.-1985.-Vol.l7.-P 154-182.

• 6    Carbone V. Scale similarity of velocity structure functions in folly developed MHD turbulence /7 Phys.Rev.E.-1994.-Vol.50 -P.671-674.

• 7.    Biscamp D Cascade model for magnetohydrodynamic turbulence // Phys.Rev.E.-1994 -Vol. 50.-№4.-P.2702-2711.

Получено 10.04.2000