Каустическая и лучевая структуры отраженных радиоволн в линейном плазменном слое

В работе предполагается, что точечный источник излучения помещен в начало координат (0, 0), а эффективная диэлектрическая проницаемость среды распространения меняется по закону:

e ( z ) = 1 - -^ z ,              (1)

to где z - вертикальная координата, ю - круговая частота излучения, а параметр у равен:

to 2 Y = —.

zm

В формуле (2) юс - это некоторая характерная частота. В настоящей работе предполагалось, что юс = ю = 13,5^106 2п об./c. При этом zm – это высота точки отражения вертикального луча. В настоящей работе расчеты выполнялись при zm = 300 км.

Хорошо известно [1] (см. также [2–4]), что бихарактеристическую систему уравнений Га- мильтона можно записать в виде:

dk _ dto1 e / со?£ dt d r     d to ’ где

dr dt

—— k = (kx , kz )

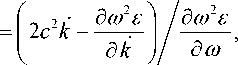
- волновой вектор, r _ ( x , z ) -

координаты точки наблюдения, с _ 2,997925^1010 см/c – скорость света, а t – параметр вдоль лучевой траектории, имеющий смысл группового времени. Эта система является следствием дис- персионного соотношения:

k x ² + k z _ £ ^to ^.              (4)

c

Учитывая, что диэлектрическая проницаемость имеет вид (1), бихарактеристическая система (3) может быть переписана как:

dkx _ о   dkz _ Y dt ’ dt 2го

В координатах ( x , z ) уравнение луча – это па-

dx c ²

— _ —k,, dt го

dz dt

_ c ² k z . го

рабола:                   2

Y x z _--2---2— + xtga.

4 го cos a

Решение системы (5) очевидно:

c ²

k x _ k x _ const ,      x _ — k x t + x 0 ,

го

На рис. 1 графически показано рассмотренное выше семейство лучей. Этот результат хорошо известен. Положение каустики (огибающей семейства лучей) на рисунке не вызывает сомнений.

к _- — t + К0, zz ,

2 го

c

z _ c--- ^Y t ² + k z t

4 го

го

+ z 0 .

Для вычисления положения каустики необходимо рассмотреть якобиан, описывающий расходимость лучевой трубки:

Лучи и каустика первичной волны

Для однозначного определения траекторий лучей в плазме необходимо задать начальные условия (при t _ 0). Как уже было отмечено выше, источник излучения расположен в начале координат, то есть x 0 _ 0 и z 0 _ 0. Поскольку источник излучения точечный, начальный волновой вектор параметрически зависит от угла α выхода луча:

^kx ^_ k x ^{(0) _} — cos a , k z ^_ k z ^{(0) _} — sin а . (7) cc

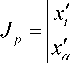
z ‘ _ c_ k x k z _ cL z' a го x'_a z'_a го

Из формул (8) следует, что

x’_a _- ct sin a ,     z ^ _ ct cos a .         (11)

Поэтому в данной задаче якобиан J равен:

J _ ct

го Y . ■

---1 sin a

v c 2 го

Тогда бихарактеристическая система (6) принимает вид:

, го kx _ — cos а, c

x _ c t cos a ,

На рис. 2 графически показано семейство якобианов, вычисленных вдоль лучей. Верхние кривые соответствуют малым значениям угла выхода α . На каустике якобиан обращается в нуль. Приравнивая к нулю выражение (12), находим два значения: t _ 0 (источник излучения) и

, Y . . го .

к _ - t +  sin a,

2 го c

2 f

c Y л . .го .

z _—--1 +1—sin a

го ( 4 го c

2 го ²

Ч _——      < cYsin а

– групповое время прихода луча на каустику.

z, км

200              400              600

Рис. 1. Лучи точечного источника в линейном слое. Число лучей 89

x , км

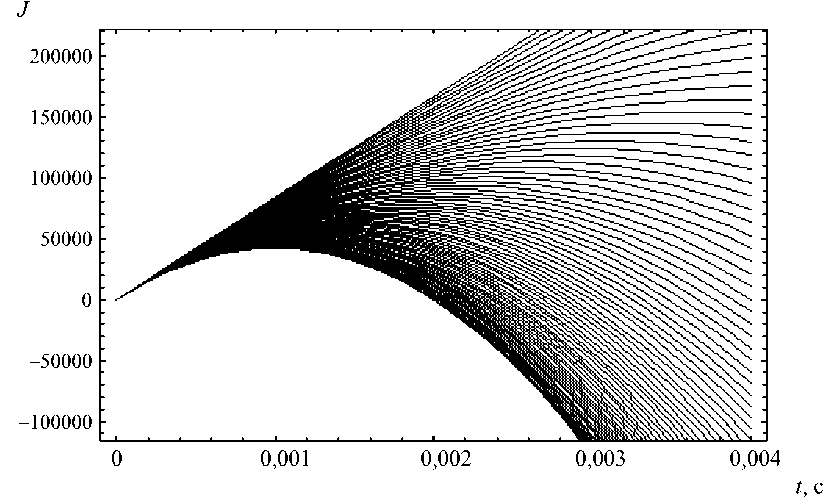
Рис. 2. Якобианы вдоль лучей в линейном слое

Подставляя (13) в (8), находим параметрическое уравнение каустики:

или, исключая параметр α , явное уравнение:

2 го2               го2 cos2a xk =    ctga, zk =---—

у               у sin a

го , zk =— 1 -

Y x k

2 го²

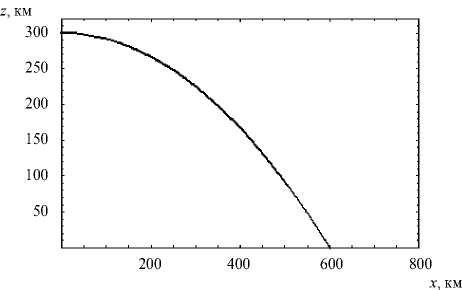
Рис. 3. Каустика первичных лучей

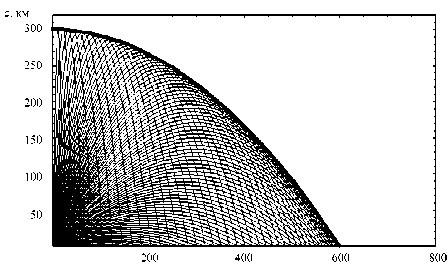
Рис. 4. Каустика и лучевое семейство

x, км

На рис. 3 представлена каустика в линейном слое, а на рис. 4 показано одновременно лучевое семейство и каустика (толстой линией). Из (8) видно, что, выйдя из источника, луч приходит обратно на линию z = 0 за время:

t_r =----- sin a.              (16)

cy

Этому времени соответствуют:

Групповое время тем больше, чем больше значение угла выхода луча α . Поворот линии соответствует каустике. Интересно отметить, что вертикальный луч приходит в точку отражения в линейном плазменном слое за время вдвое большее ( ~ 2 мс ), чем в свободном пространстве ( ~ 1 мс ).

На рис. 6 показана ионограмма наклонного зондирования в точке ( x_r =300 км, z = 0), то есть

k z ,

го .

--sin a , c

2 го x_r =----sin2 a .

Y

зависимость группового времени прихода луча

от частоты f_r , вычисленная по формулам:

На рис. 5 показана зависимость группового времени от горизонтальной координаты x_r .

tr

2 x_r sin a c sin 2 a

f = 1     Yxr r 2п 2sin2a

.

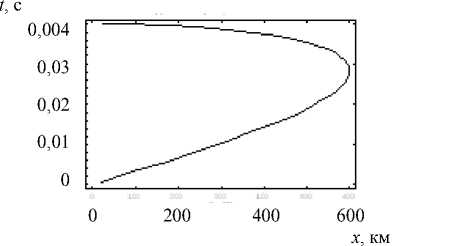
Рис. 5. Зависимость группового времени от x

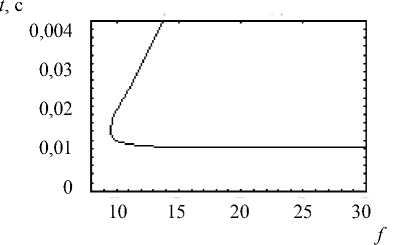
Рис. 6. Ионограмма наклонного зондирования

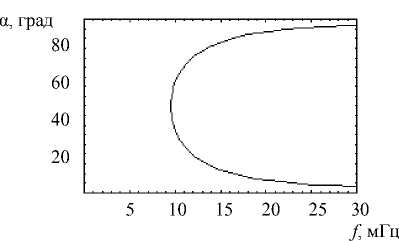
Рис. 7. Зависимость угла прихода луча от частоты

Поворот графика также соответствует каустике.

На рис. 7 представлена зависимость угла прихода луча в точку с координатами ( x_r =300 км, z = 0) от частоты.

Лучи и каустики отраженной волны первого порядка

Теперь рассмотрим лучевую структуру волн, зеркально отраженных от линии z = 0. Значение компоненты волнового вектора kx не меняется. Условием отражения луча является смена знака z-ой компоненты волнового вектора на поверх- ности отражения. Подставляя в качестве начальных данных формулы (17) в (6) и меняя знак у z-ой компоненты волнового вектора, получаем бихарактеристическую систему для отраженных волн первого порядка:

, ю                .          1 ю2 . „ kx 1 = —cos a, x1 = ct 1 cos a +----sin2a,

, c

Yю k = -    L + sin a, z,11

2 ю

• 2 fA

• c Y 2 ю .1

• = —--12 + L1—sin a \.(19)

ю ( 4ю c )

200     400      600    800     1000    1200    1400

Рис. 8. Структура отраженных лучей

x, км

Здесь индексом «1» отмечены все величины, относящиеся к семейству отраженных лучей, в том числе и групповое время, отсчитанное от точки отражения. Поэтому общее групповое время – это сумма t_r + t ₁.

В координатах ( x , z ) уравнение луча по-прежнему парабола:

z, =--;-- 1—

4 го ² cos² а

ГО 2

+ 3 x 1 tg а - 8—sin а , (20) Y

нее в работе [5], посвященной распространению излучения в неоднородном волноводе.

Для вычисления положения каустики, как и в случае первичной волны, необходимо рассмотреть якобиан J ₁ описывающий расходимость лучевой трубки отраженных лучей. Он определяется формулой (10), однако теперь меняется выражение для производной х'_а :

однако лучевая структура иная (рис. 8). Очевидно, что кроме охватывающей каустики (катастрофа A₂) возникает еще и каустическое острие (катастрофа A₃), образующие единую каустическую структуру (катастрофа D 4 ). Необходимо отметить, что образование двумерной катастрофы D 4 в двумерных случаях было отмечено ра-

4 го ²

\_а = - c t 1 sin а +---- cos 2 а ,

,                       Y z'^ = c t1 cos а,

а компоненты волновых векторов и z ₁

J 1 600000

ся неизменными. Тогда якобиан J равен: ¹

т . го Y . ■ I .

J 1 = ct 1--- 1 1 sin а 1 +

(c 2ro )

^{2 ro}         I

+ 2 гo cos2 а t 1-- sin а \ .

cY     )

остают- 1, ^а

–200000

–400000

–60000

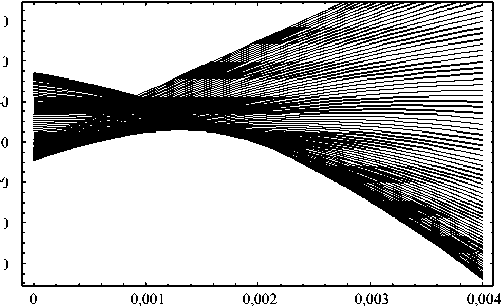
Рис. 9. Якобианы вдоль отраженных лучей

t , с

На рис. 9 представлено семейство якобианов, вычисленных вдоль отраженных лучей. Верхние кривые в правом верхнем углу соответствуют малым значениям угла выхода α . Как и в случае первичных лучей, на каустике отраженных лучей якобиан обращается в нуль. Приравнивая к нулю выражение (22), находим два значения

Подставляя (23) в (19), находим параметрическое уравнение каустики:

' 1,k ( ± )

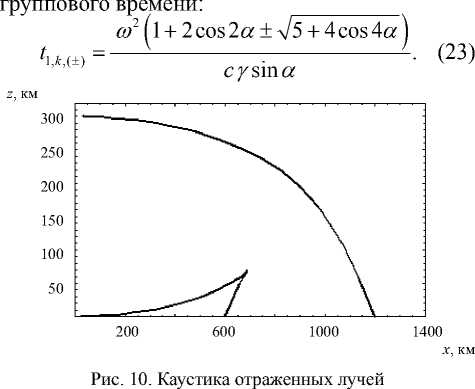
го2 (V5 + 4cos4а ± 3)= ±--------------------- ctgа,

Y

z 1,k ( ± )

ГО 1 + 8 cos 2 а ± 3^5 + 4cos4 а

I у                                j cos ^а sin2 а

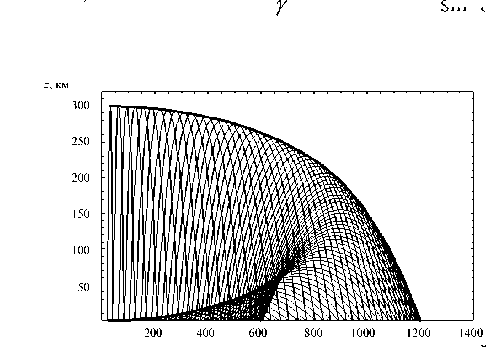
Рис. 11. Каустики и отраженные лучи

.

, км

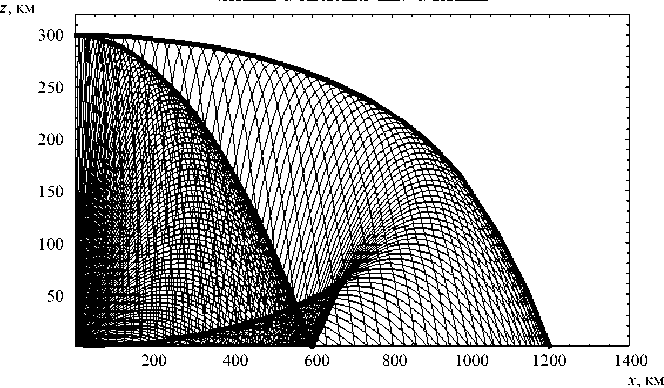
Рис. 12. Первичные и отраженные лучи и каустики

На рис. 10 показана каустика отраженных лучей. каустическое острие соответствует нижнему знаку в формулах (23), (24) (знак «–»), а охватывающая каустика – верхнему знаку (знак «+»). Необходимо обратить внимание, что верхняя ветвь каустического острия уходит в источник излучения. На рис. 11 представлено одновременно семейство отраженных лучей и каустика (толстой линией), а на рис. 12 каустики и лучи – как первичных, так и отраженных волн.

Видно, что нижняя ветвь каустического острия является как бы отраженной каусти- кой по отношению к каустике первичной волны. Упоминания об отраженных каустиках можно найти в работах [6], [7]. Более подробно каустики отраженных лучей были рассмотрены в [2].

Отраженный луч приходит обратно на линию z = 0 за локальное время t _{1 r} = t_r (см. формулу (16)). Поэтому суммарное групповое время равно 2 t_r . При этом горизонтальная координата также удваивается:

4 ω ²

x =      sin 2 α .

, r

γ

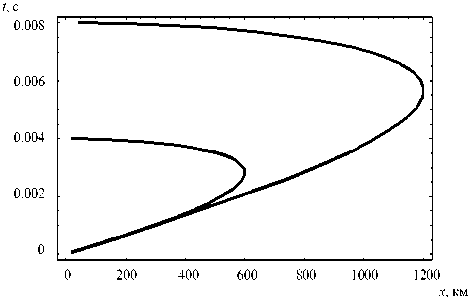
Рис. 13. Зависимость группового времени от координаты x

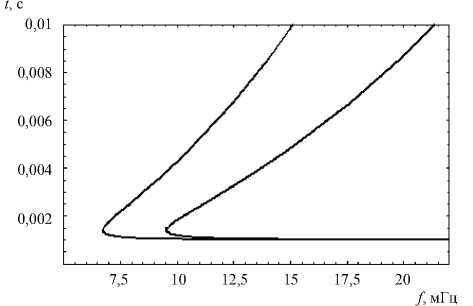
Рис. 14. Ионограммы наклонного зондирования

На рис. 13 показана зависимость группового времени прихода первичного и вторичного лучей от координаты x . Большая кривая соответствует отраженным лучам. Интересно отметить, что наличие нижней ветви каустики никак не влияет на форму этой кривой, которая подобна зависимости группового времени первичных лучей (малая кривая). На рис. 14 представлена ионограмма наклонного зондирования в точке ( x_r =300 км, z = 0), то есть зависимость группово-

го времени прихода луча от частоты, вычисленная по формулам (18) для первичных лучей и по формулам:

t =    ^{x r}      f = ^{1      γ x r}

^{1, r , s} c cos α ,    ^{1, r} 2 π 4sin2 α

.

для отраженных лучей. Левая кривая соответствует отраженным лучам, правая – первичным. Верхняя часть графика соответствует большим углам α выхода луча. Точки поворота графиков указывают на положение внешних каустик.

Лучи и каустики отраженных волн второго и болеe высоких порядков

Обобщая результаты, полученные в предыдущих разделах, нетрудно убедиться, что биха-рактеристическая система для отраженных волн m -ого порядка имеет вид:

Y

2 = —-+ zm22

4 m ( m + 1) to ² . ₂

+ (1 + 2 m ) x tg a -               sin² a .   ⁽²⁸⁾

to k x , m = -cos ^a , c

. 2 m to¹ . „ x_m = c t m cos a +------ sin 2 a ,

Y

Y

Для вычисления положения каустики отраженных лучей m -ого порядка необходимо найти нули якобиана J_m . Так как производные координат по параметру α имеют вид:

4 m to ²

x_m , _a = - c t_m sin a +------ cos 2 a ,

,           Y to .

^k. , m =- — tm ⁺ "sin ^a ,

2 to c c Y 2 to . I         /ОЛА

Z m =-- "J- t m + t m sin « I ,        ⁽²⁷⁾

to ^ 4 to         c )

где m = 0 соответствует первичной волне, m = 1 – отраженной волне, рассмотренной в предыдущем разделе, и т.д. Форма луча при всех отражениях – это парабола:

^Y z m, a = ^ctm cos ^a , то якобиан J_m равен:

r           to Y

mm

c

--t„ sin a +

2m to I

+ 2 to cos2 a t_m

2 m to ² .      1

--------sin a I .

c Y )

500             1000            1500            2000

Рис. 15. Лучевые и каустические структуры, m = 3

Приравнивая к нулю выражение (30), находим два значения группового времени:

t m , k ,( ± )

юг

( 1 + 2 m cos 2 a ± ^ 1 + 2 m + 2 m ² + 2 m (1 + m )cos4 a )

,

, to ² cos 2 a z x> ( ± ) =±---—— ^x

Ysin a x (1 + 4m(1 + m) cos 2a ±

cYsin a а подставляя (31) в (27), получаем параметрическое уравнение каустики:

± (1 + 2 m )^/1 + 2 m + 2 m ² + 2 m (1 + m )cos4 a ) .

x m , k ( ± )

to ² ( 1 + 2 m ± 1 + 2 m + 2 m ² + 2 m (1 + m ) cos 4 a )

— ------------------------------- ctg a ,

Y

На рис. 15 показаны лучевые и каустические структуры первичной и трех отраженных волн. Видно, что вдоль отражающей линии стелется верхняя ветвь каустического острия, причем на определенных расстояниях, расположенных квазипериодически, волна как бы высвечивается вверх. Фактически это лучевая интерпретация образования поверхностной волны.

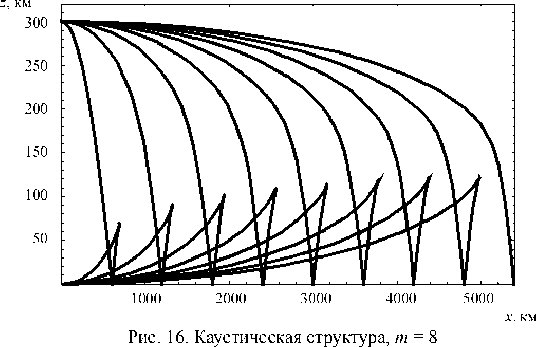
только каустическая

На рис. 16 показана

структура при m = 8, а на рис. 17 и 18 (точками) положения центров каустического острия

Видно, что при увеличении порядка отражения центры каустического острия удаляются вправо, а их вертикальная координата медленно, но воз-

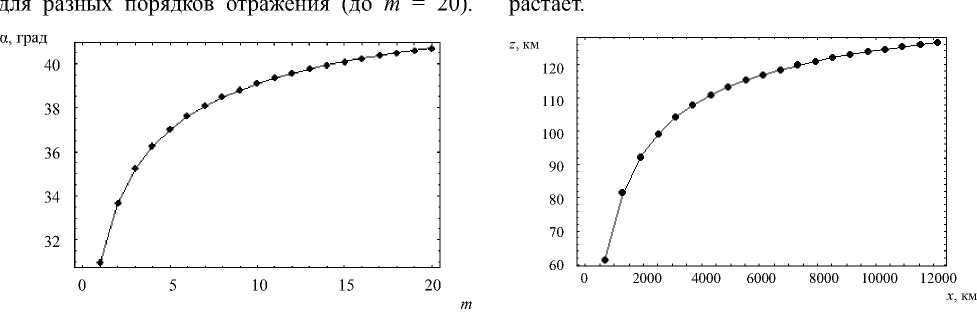
Рис. 18. Положения центров каустического острия. Координаты ( x , z )

Рис. 17. Положения центров каустического острия. Зависимость угла выхода от порядка отражения

Положения центров каустического острия определялись численно. Приравнивая к нулю производную якобиана по параметру выхода луча α (дополнительное уравнение для определения положения центра каустического острия)

J=о, 5 a

находился угол α_с . Зная угол α_с , из формул (32)

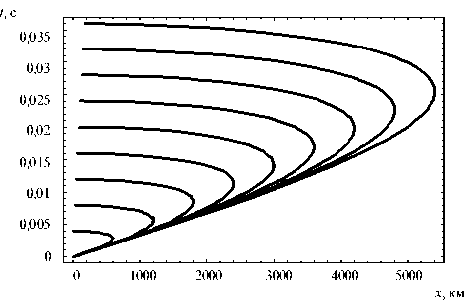
Рис. 19. Зависимость группового времени от координаты x нетрудно найти декартовы координаты каустического острия.

Отраженный луч m -ого порядка приходит обратно на линию z = 0 за локальное время t m r = t r (см. формулу (16)). Поэтому суммарное гру^,ппо-вое время равно ( m + 1) t_r . Тогда горизонтальная координата имеет вид:

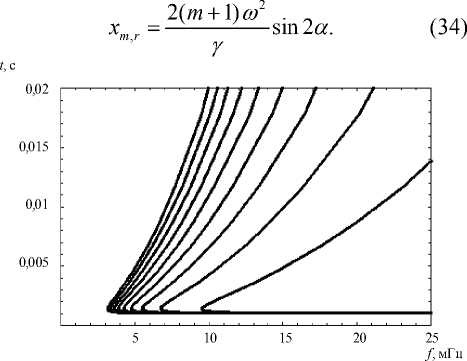
Рис. 20. Ионограммы наклонного зондирования

На рис. 19 показана зависимость от координаты x группового времени прихода первичного и отраженных лучей до восьмого порядка включительно. Самая маленькая кривая соответствует первичным лучам. На рис. 20 представлена ионограмма наклонного зондирования в точке ( x_r =300 км, z = 0), то есть зависимость группового времени прихода луча от частоты, вычисленная по формулам (18) для первичных лучей и по формулам:

t  = —x r —, f = — I ^Yx (35)

m,r, s        ____, f m r c cos a     ' 2n (m + 1)sin2a для отраженных лучей. Внутренняя кривая соответствует первичным лучам. Точки поворота графиков указывают на положение внешних каустик.

Естественно возникает вопрос: как изменится вид ионограмм, если точка наблюдения несколько приподнята, то есть ее координаты будут

(X, Z). Находим локальное время прихода луча в эту точку:

t_L ± = —( to ² sin a ± to Ji

, cy to2 sin2 a - Zy). (36)

Таким образом, если подкоренное выражение неотрицательно, то в точку с высотой z = Z приходят два луча рассматриваемого лучевого семейства, а не один, как в предыдущем случае. Каждому групповому времени (36) соответствует своя координата x :

x_L =— ( (1 + 2 m )to ²sin2 a - 2 to cos aJto ² sin ² a - Z y ) , (37)

^{, _} Y

2cos a 2             2 .     .

x_L , ₊ =------ ( m to sin 2 a + to sin a + to to sin a - Z y ) . (38)

На рис. 21 показана зависимость суммарного группового времени mt_r + t_L ± прихода первичного и отраженных лучей до восьмого порядка от координаты x (формулы (37), (38)).

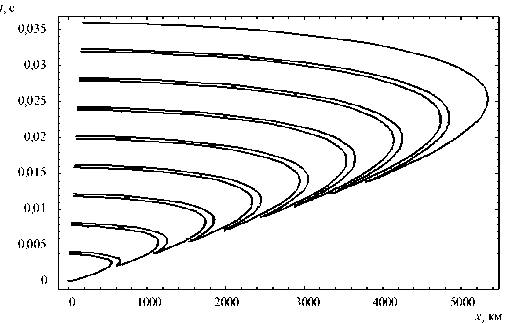
Рис. 21. Зависимость суммарного группового времени от x , Z = 50 км

Если сравнить рисунки 19 и 21, видны существенные качественные различия. На рис. 19 линии, соответствующие отраженным лучам, охватывают друг друга. На рис. 21 этого не происходит. Возникает точка возврата, и нижняя ветвь t с

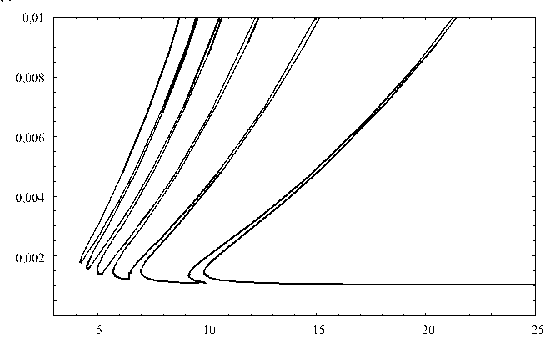
Рис. 22. Ионограммы отраженных лучей, Z = 20 км, m = 5

отраженных лучей следующего порядка как бы стелется по верхней ветви лучей предыдущего порядка. При малых высотах их различить невозможно, поэтому происходит уширение линий.

f , мГц

На рис. 22 представлены ионограммы наклонного зондирования. Для их вычисления из уравнений

X X (39)

определялись частоты (формулы явные, но громоздкие, поэтому здесь не приводятся), а суммарное групповое время определялось, как и выше, формулой:

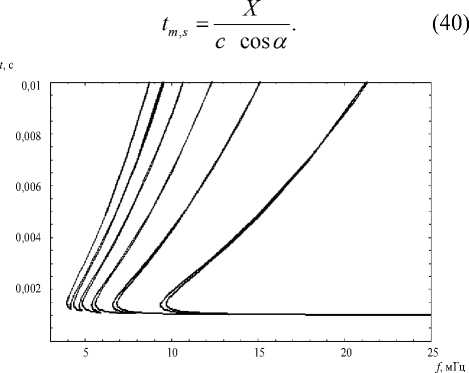
Рис. 23 Ионограммы отраженных лучей, Z = 10 км, m = 5

В реальных наблюдениях это приведет к уширению как верхней ветви ионограммы первичных лучей, так и максимума. Для сравнения на рис. 23 и 24 приведены ионограммы на высотах 10 км и 50 км соответственно.

В завершении работы приведем без подробного обсуждения графики фазы лучей вдоль линии Z = 0:

Сравним рис. 22 и 20. Следует обратить внимание на ионограмму отраженных лучей первого порядка. Если на рис. 20 ее нижняя ветвь сливалась с нижней вервью ионограммы первичных лучей, то теперь формируется точка каустического острия (точка возврата), после которой ветвь, делая разворот вокруг максимума ионограммы первичных лучей, начинает асимптотически стремиться к верхней ветви ионограммы первичных лучей.

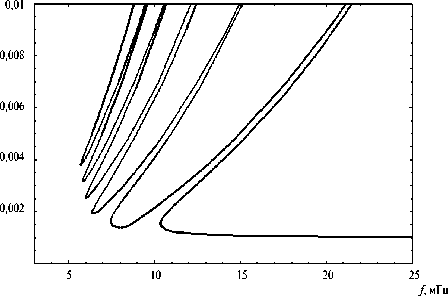
Рис. 24. Ионограммы отраженных лучей, Z = 50 км, m = 5

4(1 + m)„

Ф _тг = ~---- ^L(O (2 + cos 2 ^ )sin a ,

,

2( m +1) to2 xmr = ~-----—sin2a.

’

Видно, как два соседних порядка образуют сечение особенности «ласточкин хвост» (катастрофа А4).

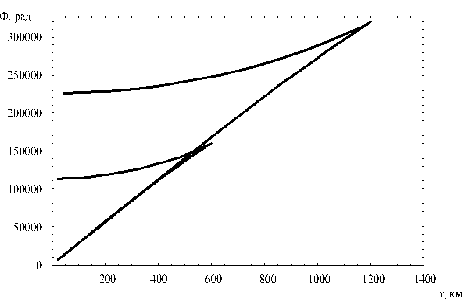
Рис. 25. Фазы лучей вдоль линии Z = 0, m = 1

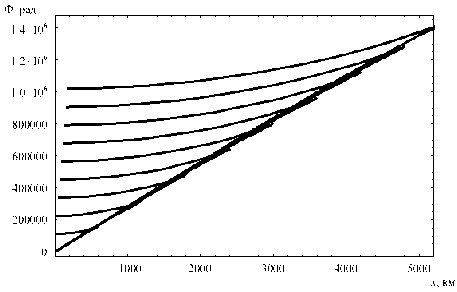
Рис. 26. Фазы лучей вдоль линии Z = 0, m = 8

Заключение

Таким образом, в настоящей работе рассмотрены лучевые и каустические структуры, возникающие при распространении электромагнитных волн в плазменном слое с линейно уменьшающейся высотой эффективной диэлектрической проницаемостью среды распространения.

Исследованы лучевые и каустические структуры отраженных лучей разных порядков, возникающих при многоскачковом распространении, ионограммы наклонного зондирования, структуры якобианов, фазовые и групповые зависимости. Показано, что каустическая структура отраженных волн соответствует гиперболическим омби- ликам (катастрофа D4+), а учет отражения приводит к уширению ионограмм.

Автор выражает благодарность д.ф.-м.н., профессору Д.С. Лукину и д.ф.-м.н. А.П. Анютину за внимание к работе и полезные консультации.