Каустическая структура краевой катастрофы K 4,2

ВЕСТНИК 2015

Настоящая1 работа2 посвящена исследованию каустической структуры3 краевой катастрофы K4,2, описывающей унимодальную каспо-идную фокусировку первичных и вторичных лучевых семейств. Как показано в работах [1–4], волновая катастрофа K4,2 возникает как в задачах стационарной дифракции, когда и первичное, и вторичное излучение имеет особенность каспо-идного типа А3, так и в нестационарных задачах распространения электромагнитных сигналов при совместной фокусировке пространственных и временных лучевых семейств.

Как известно [1–4], универсальная деформация катастрофы K_4,2 имеет вид:

F K^ = k 1 z ² + ax ² z + k 2 x ⁴ +

+ 2 x + 2 2 x ² + 2 3 z + 2 4 xz ,                  (1)

где x и z – внутренние переменные, a – функциональный модуль, а λ1, λ2, λ3, λ4 – коэффициенты универсальной деформации, причем z е [0,+^) , x е (—»,+<»). В соответствии с необходимыми и достаточными условиями образования катастрофы K4,2 [4–8], на функциональный модуль a накладываются ограничения [9]:

a ² *± 4. (2)

Для того чтобы получить каустику (огибающую семейства краевых лучей), необходимо дополнить уравнение (7) нулем второй производной функции (6) по x :

12 k ₂ x ² + 2 4 2 = 0. (8)

Параметры k ₁ и k ₂ принимают значения +1 или –1.

Равномерная асимптотика, соответствующая рассматриваемой особенности, имеет вид [2]:

В результате найдем уравнение каустики в параметрической форме:

4 1 = 8 k ₂ x ³

4 2 = - 6 k ₂ x ²

U ( r, t ) = e”

{ ( ' 1 ) K

(a; 4)+Е( lk) g k=3

5 I K 4,2 "5 4

+

Рассмотрим теперь каустику ГО лучей. Лучевые уравнения получаются дифференцированием универсальной деформации (1) по внутрен-

2       л / a

+(к) .i A3 (41, 4 )+K lk) E ^M, k=1      d 4

ним переменным x и z :

где I^{K 4,2} ( a , 4 ) =

4 1 = - 4 k ₂ x ³ - 2 a x z - 2 4 2 x - 4 4 z

4 3 =- ax ² - 2 k 1 z - 4 4 x

+to +to

= j dz j exp { i ( k 1 z ² + ax ² z + k ₂ x ⁴ + 4 1 x +

0 -to

+ 4 2 x ² + 4 3 z + 4 4 xz ) } dx                    (4)

Для того чтобы получить каустику ГО лучей, необходимо дополнить уравнения (10) нулем Гессиана универсальной деформации (1) по внутренним переменным:

ВЕСТНИК 2015

спецфункция (СВК) краевой катастрофы K_4,2 (в показателе экспоненты стоит универсальная деформация (1)), а

+to

I^{A 3} ( 4 1 , 4 2 ) = j exp { i ( k ₂ x ⁴ + 4 2 x ² + 4 1 x ) } dx (5)

-to

функция Пирси, то есть СВК основной катастрофы А₃ . Её универсальная деформация получается как сужение исходной универсальной деформации с помощью подстановки z = 0. В формуле (3) θ – фаза бегущей волны, а ( l_j ) _g и ( l_j ) _E – геометрооптические (ГО) и краевые коэффициенты асимптотического разложения.

Рассмотрим каустические структуры катастрофы K_4,2 . Во-первых, отметим, что разложение катастрофы K_4,2 на основную особенность и катастрофу сужения имеет вид [2; 6]: K ₄₂ = (A₃,A₃), то есть обе особенности представляют собой каустическое остриё. Только ГО каустическое остриё имеет обрыв. Поэтому каустики (огибающие семейство ГО и краевых лучей) будут иметь форму клювов, причем связывает их прямая – граница свет-тень.

Рассмотрим сначала краевые лучи. Уравнения краевых лучей получаются из дифференцирования сужения ( z = 0) исходной универсальной деформации (1), имеющей вид:

F_a = k ₂ x ⁴ + 4 2 x ² + 4 1 x (6) по параметру x и приравниванием результата нулю:

4 1 =- 4 k ₂ x ³ - 2 4 2 x . (7)

det

d ² F_K

K 4,2

d x ²

d ² F_K

K 4,2 d x d z

d ² F_K

K 4,2 d x d z d ² F_K

K 4,2 d z²

= 0.

Подставляя (1) в (11), получаем:

2 k 1 (12 k ₂ x ² + 2 az + 2 4 2 ) - (2 ax + 4 4 )² = 0, (12)

откуда находим внутренний параметр z :

(2 ax + 4 4 )² - 24 k 1 k ₂ x ² - 4 k 1 4 2 z =--------------------------

4 k ₁ a

.

Подставив (13) в (10) и выполнив соответствующие преобразования, найдем, как и в случае каустики краевых лучей, выражения для λ ₁ и λ ₂:

4=

42 =

4 3 4 4 - 4 a ² x ³ + 16 k 1 k ₂ x ³ - 3 ax ² 4 4

2 k ₁

4 ₄ ² + 6 a ² x ² - 24 k 1 k ₂ x ² + 2 a 4 3 + 6 ax 4 ₄

. (14)

4 k ₁

Для того чтобы получить уравнение границы свет-тень, подставим z = 0 в систему (10) и, вы-

полнив преобразования, найдем, что:		(15)
	4 1 =- 2 xb 4 2 - 4 k 2 x b 3,
где
	- 4 4 + J42 - 4 a 4 3 x b = x b 2 =        ,	(16)
	2 a
или
	- 4 4 - J 4 4 2 - 4 a 4 3 x b = x b 1 =       \           . 2 a	(17)

На рис. 1–9 показаны каустические структуры катастрофы K_4,2 в плоскости ( λ ₁, λ ₂) при различных значениях параметров λ ₃, λ ₄ и функционального модуля a. Толстой линией на рисунках показана каустика ГО лучей. Её аналитическое продолжение, отсекаемое границей свет-тень, показано штриховой линией (пунктиром). Штрихпунктирной линией показана граница свет-тень. Наконец, тонкой линией показана каустика краевых лучей.

Сначала рассмотрим случай, когда параметры λ ₃, λ ₄ равны нулю. Рис. 1 соответствует случаю a = 0.

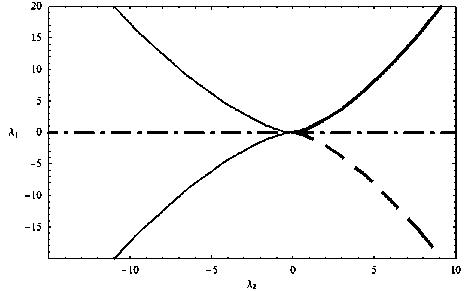
Рис. 3. a = 2,5; k ₁ = k ₂ = 1, λ ₃ = λ ₄ = 0

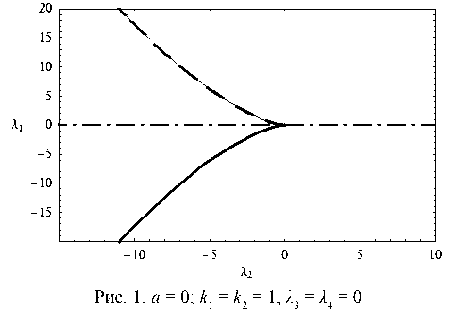
Каустика краевых лучей (каустическое остриё) совпадает с каустикой ГО и её продолжением, граница свет-тень является биссектрисой.

При увеличении функционального модуля a каустика ГО лучей (и её продолжение) отрывается от каустики краевых лучей (рис. 2) и стремится при a → 2 к вертикали, что является вырожденным случаем.

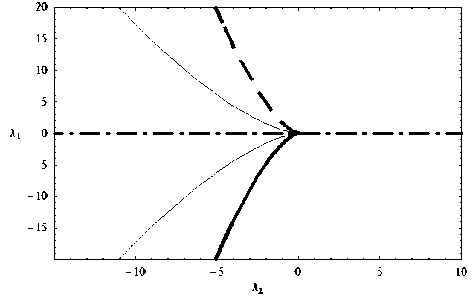
Рис. 2. a = 1,9; k ₁ = k ₂ = 1, λ ₃ = λ ₄ = 0

В случае когда функциональный модуль превосходит 2 (рис. 3), остриё ГО лучей отображается относительно острия краевых лучей в правую часть рисунка.

Необходимо отметить, что на рис. 1–3 при всех значениях функционального модуля точка с координатами (0,0) является особой точкой катастрофы K4,2 , так как изменение функционального модуля не устраняет особенности.

Рассмотрим теперь случаи, когда параметры λ ₃ и λ ₄ не равны нулю. На рис. 4 показан случай, когда и λ ₃, и λ ₄ не равны нулю, но разных знаков.

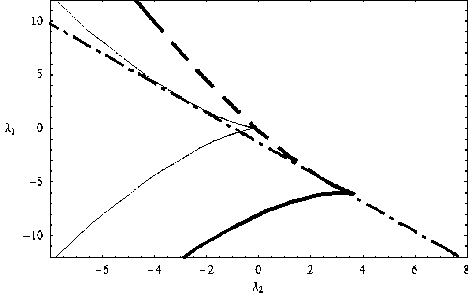
Рис. 4. a = 0,5; k ₁ = k ₂ = 1, λ ₃ = –3, λ ₄ = 4

ВЕСТНИК 2015

Поскольку a меньше 2, оба каустических острия смотрят вправо, в разных точках касаются границы свет-тень и смещены относительно друг друга. Для вычисления x_b использовалась формула (16).

Аналогичная картина возникает, если поменять знак у функционального модуля (рис. 5).

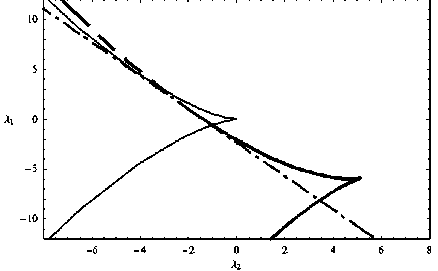
Рис. 5. a = –0,5; k ₁ = k ₂ = 1, λ ₃ = –3, λ ₄ = 4

Пусть теперь функциональный модуль превышает 2, причем k ₂ принимает значение не +1, а –1 (рис. 6).

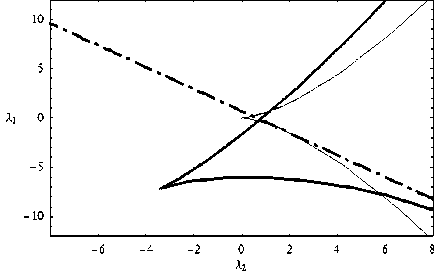
Рис. 6. a = 2,5; k ₁ = 1, k ₂ = –1, λ ₃ = –3, λ ₄ = 4

Видно, что оба каустических острия смотрят влево, причём каустическое остриё краевых лучей отстаёт от каустического острия ГО лучей. Для вычисления x_b по-прежнему использовалась формула (16).

Поменяем знак функционального модуля и знаки у λ ₃ и λ ₄ (рис. 7).

ВЕСТНИК 2015

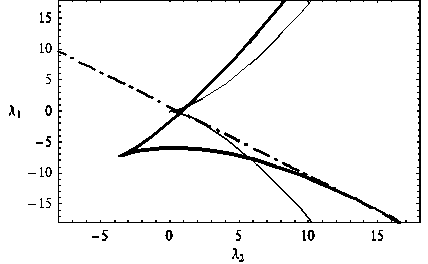
Рис. 7. a = –2,5; k ₁ = 1, k ₂ = –1, λ ₃ = 3, λ ₄ = –4

Видно, что картина качественно не изменилась, но для вычисления x_b теперь уже используется формула (17).

Поменяем знак у k ₁ с плюса на минус и сохраним неизменными остальные параметры.

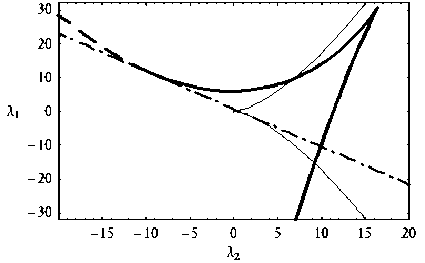
Рис. 8. a = –2,5; k ₁ = –1, k ₂ = –1, λ ₃ = 3, λ ₄ = –4

Теперь каустическое остриё краевых лучей (которое осталось на месте) и каустическое остриё ГО лучей смотрят в разные стороны. Для вычисления x_b используется формула (17).

Наконец, рассмотрим случай, когда граница свет-тень отрезает полностью каустическое остриё ГО лучей, оставляя только каустику с краем (рис. 9).

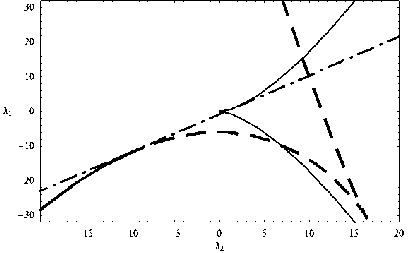
Рис. 9. a = 2,5; k ₁ = –1, k ₂ = –1, λ ₃ = –3, λ ₄ = –4 или a = –2,5; k ₁ = –1, k ₂ = –1, λ ₃ = 3, λ ₄ = 4

Это возможно в двух случаях: когда функциональный модуль положительный, а параметры λ ₃, λ ₄ отрицательные, либо наоборот – функциональный модуль отрицательный, а параметры λ ₃, λ ₄ положительные. В первом случае для вычисления x_b используется формула (17), а во втором – формула (16).

Таким образом, в настоящей работе исследована каустическая структура краевой катастрофы K₄₂ = (A3, A3) , распадающейся две каспоид-ные катастрофы A3 , соответствующие каустикам семейств краевых и ГО лучей [1; 2; 6]. Катастрофы каспоидного такого типа возникают в задачах распространения и дифракции волн и соответствуют областям фокусировок (см., например, [3; 13; 14]). Краевые катастрофы возникают при совместной пространственной и временной фокусировке электромагнитного излучения волны в плазменном слое с сильной частотной дисперсией [3; 4]. Для описания электромагнитных полей в таких областях разработана волновая теория катастроф [1; 2; 6], опирающаяся как на классические результаты теории катастроф [9], так и на лучевые методы [15–17].

Приведены каустические структуры краевой катастрофы K₄₂ при различных коэффициентах универсальной деформации и функционального модуля.