Кавитация в элементах запорной арматуры трубопроводных систем

Кавитацией принято называть явление парообразования и выделения воздуха (газов), обусловленное понижением давления в жидкости, или так называемое холодное кипение жидкости. Из интеграла Бернулли следует, что при установившемся движении жидкости распределение давлений в потоке существенно зависит от распределения скоростей. Для несжимаемой жидкости уравнение Бернулли имеет вид

QZ + р + у = const . (1)

Из него следует, что при движении несжимаемой жидкости в некоторых частях потока давление может иметь отрицательное значение или даже равняться минус бесконечности.

Диаграмма Ван-дер-Ваальса дает хорошее представление об ожидаемом поведении жидкости, если давление непрерывно падает при постоянной температуре. Если проследить изменение давления на P-V –диаграмме (рис. 1) от точки A до точки C по изотерме A-D-B-E-C , то в точке A оно достигает той величины, при которой обычно возникает парообразование.

В дальнейшем будет наблюдаться переход жидкости в пар при постоянном давлении (T = const), чему соответствует линия A-B-C . После того как вся жидкость перейдет в пар, растяжение приведет к снижению давления в системе. В точке A следует ожидать начала возникновения кавитации. В особых условиях (дегазированная жидкость, чистый сосуд, отсутствие вибрации) удается подойти через точку A к точке D , а при достаточно низких температурах (например, комнатная для воды) изотерма пересечет линию нулевого давления, т.е. в жидкости возникнут напряжения растяжения. При этом каждый элемент жидкости находится в области низкого давления лишь очень короткое время.

Известно, что воду в чистом сосуде можно нагреть свыше 100 °С или охладить на несколько градусов ниже 0 °С. Перегрев, переохлаждение, а также пересыщение воды газом – хорошо известные примеры ее метастабильных состояний. Для метастабильности характерно следующее свойство: вещество мгновенно выводится из метастабильного состояния при возникновении зародышей (с размерами, большими критической величины для данных условий) другой фазы.

Из опыта известно, что жидкости не могут сопротивляться сколько-нибудь значительным напряжением растяжения. Однако, по свидетельству А. Хейуорда, впервые в 1843 г. Ф. Донни установил возможность метастабильного состояния жидкостей, при котором в них действо -вали растягивающие напряжения. Со времени Ф. Донни техника эксперимента по определению величины растягивающих напряжений постоянно совершенствовалась. Описание раз-

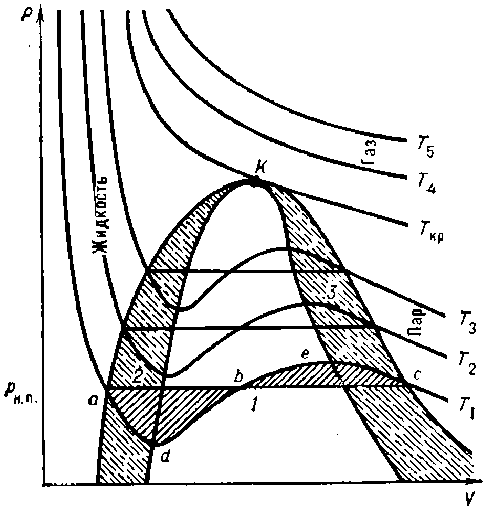
Рис. 1. Диаграмма Ван-дер-Ваальса. Возможность наступления растяжения в жидкостях личных методов, а также обзор полученных результатов изложены в монографиях [1 и др.] и в обзорной статье [2] и др.

Максимальные растягивающие напряжения центробежным методом были замерены Л. Бриггсом [2]. В опытах с ртутью ему удалось получить значения растягивающих напряжений 4,2407 Па, а с водой - 2,8407 Па. Согласно кинетической теории жидкостей чистые жидкости способны выдерживать очень высокие растяжения (отрицательные давления): от 50 до 1000 МПа [3]; по данным М.С. Плессета [4], до 1500 МПа. В настоящее время вопрос о том, предельны полученные Л. Бриггсом значения растягивающих напряжений или нет, остается неясным.

Одной из наипростейших теоретических оценок разрывных напряжений является оценка, сделанная на основании предположения, что разрыв происходит на микрополостях, размер которых по порядку величины равен среднему расстоянию между молекулами. Сделав предположение, что разрыв произойдет при достижении разрывными напряжениями величины капиллярных сил на поверхности пузырька, которыми условно заменяется микрополость, можно определить величину этих напряжений с помощью формулы Лапласа:

2 = Р.-Рж = ^.                                         (2)

дя из этой формулы, для воды (а = 1,5 • 10 ” ² М ; R = 10 ” ⁸ см) получаем значение Z = 10 9 Па.

Я.И. Френкель [5] и Я.Б. Зельдович [6] получили меньшую величину: Z = 1,6^10® Па. Их теория базируется на предположении, что разрыв происходит из-за тепловых флуктуаций в результате спонтанного возникновения паровых микрополостей, являющихся зародышами новой фазы. Вероятность возникновения паровых пузырьков с размерами R > 10-7 см согласно этой теории в воде при нормальных условиях мала, а значение Z для таких пузырьков в соответствии с (2) равно 1,5^108 Па, что хорошо согласуется с результатами более точных расчетов.

В отличие от специально поставленных лабораторных опытов с прецизионно чистой (химически и механически) водой в обычных условиях, как правило, не удается зафиксировать сколько-нибудь заметных растягивающих напряжений. В быту, технике и природе не встречаются жидкости с высокой степенью чистоты, что является непременным условием ранее указанных физических опытов. Поэтому давление в обычном потоке не может стать ниже некоторой положительной величины Pd , близкой при обычной температуре (20 °С) к нулю, т.е. к давлению насыщенных паров жидкости, которое зависит от температуры и свойств этой жидкости.

При падении давления в потоке до значения P_d происходит нарушение сплошности течения и образуется область, заполненная паровыми или газовыми пузырьками, т.е. происходит фазовый переход первого рода при умеренных или низких температурах - кавитация («холодное кипение»).

Теоретически холодное кипение в жидкости начинается при P_кр = P_d . Однако, как отмечает И. Пирсол и другие исследователи, при наличии в жидкости большого количества растворенного воздуха снижение давления приводит к его выделению и образованию газовых каверн, в которых давление выше, чем давление насыщенных паров жидкости. При наличии в жидкости микроскопических пузырьков кавитация может возникать при давлении P _кр > P_d . Опыт и физические теории, утверждает академик Л.И. Седов, указывают на то, что даже в обычных условиях в короткие промежутки времени в жидкости могут возникать ограниченные по величине отрицательные давления, вызывающие внутренние растяжения. При отсутствии действительных разрывов и кипения, например, обычная водопроводная вода может выдерживать очень короткое время растяжение до четырех атмосфер.

Очевидно, что причиной низкой объемной прочности в повседневной практике является загрязненность жидкости другими веществами и нерастворенными частицами. Их наличие приводит к появлению в жидкости слабых мест, получивших название кавитационных зародышей, или ядер кавитации (гипотеза Л.Я. Эпштейна-Гарвея). Детальная структура ядер окончательно не установлена. Малые размеры и неопределенность их пространственного положения существенно затрудняют наблюдение над ними.

По современным данным, в 1 см3 натуральной воды содержится до 500 тыс. ядер кавитации (микропузырьки и механические включения) с размерами от нескольких до 20 мкм. Результаты измерения спектра ядер кавитации, выполненные различными методами в дистилированной [7, 8], неотстоявшейся и отстоявшейся водопроводной воде [9, 10], представлены на рис. 2, где

n(R0)

dNR

О кр

dR0

размер ядер кавитации. Если предположить, что в жидкости присутствуют ядра с размерами от R _0min до R _0max, то концентрация ядер, способных к кавитационному росту при заданном разрежении, т.е. их количество в единице объема жидкости,

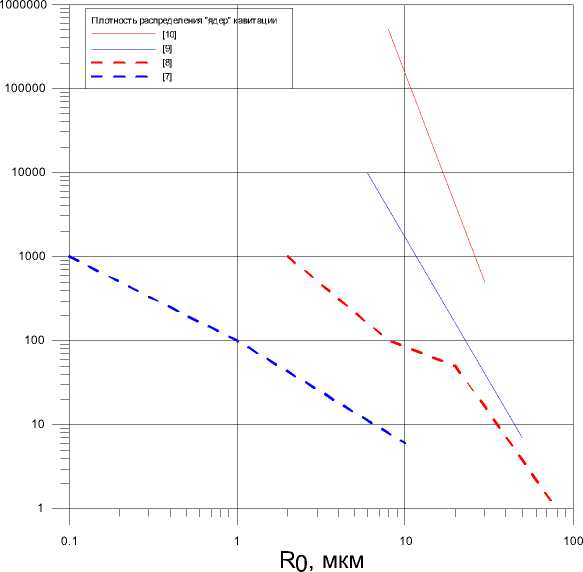
Рис. 2. Плотность распределения «ядер» кавитации по [7-10]

-rOkp = -C™*n(R0) dR0 = NRq - JR°кр n(R0) dR0,                    (4)

• о кр    ^R °mrn                    о     ^R °_mm

где NR _o - общая концентрация ядер.

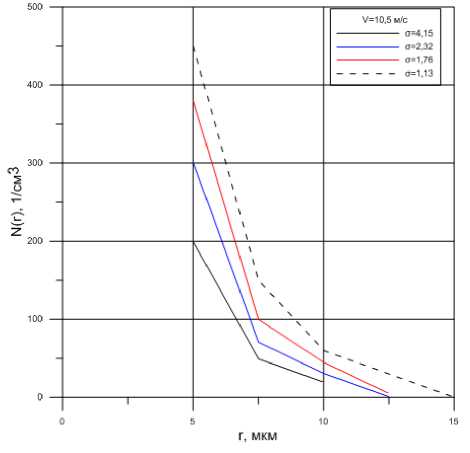
Изменение концентрации и дисперсности пузырьков нерастворенного газа в потоке движущейся жидкости может быть определено средствами гидроакустики [10, 11] , методом светорассеяния [12] или голографии. На рис. 3. показано распределение пузырьков по размерам NR . Из графиков видно, что распределение ядер кавитации в движущейся воде весьма неравномерно и зависит от скорости (давления) потока. С уменьшением числа кавитации количество свободного воздуха увеличивается.

Представляет интерес сопоставление данных, представленных на рис. 3, и результатов измерений в неподвижной воде. По данным [12], в неподвижной воде концентрация пузырьков с R = 5 мкм имеет порядок 10^-1-10^-2 1/см³. В [13] получено значение (концентрации 10² 1/см³ для частиц такого размера), что говорит о существенном влиянии движения жидкости на концентрацию ядер кавитации в ней.

Теоретические исследования и анализ литературных источников [14] применительно к клапану как объекту исследования и процессам, происходящим во время его работы, позволяют сформулировать некоторые общие выводы и наметить пути решения технической задачи обеспечения безкавитационной работы или значительного увеличения ресурса:

• 1.    Кавитация, возникающая в рабочей жидкости в клапанах, носит вибрационный характер и определяется периодически изменяющимся давлением во времени (в отличие от про-

• а)

• 2.    Возникновение и развитие кавитации слабо зависят от материала рассматриваемой системы (хотя в случае вибрационной кавитации модуль упругости материала может повлиять на перепад давления).

• 3.    Степень кавитационной эрозии существенным образом зависит от свойств материала, его структуры и микроструктуры, напряженного состояния, свойств рабочей жидкости, нали-

• чия ядер кавитации, термо- и гидродинамических параметров режима работы, шероховатости и т.п.

• 4.    При низкой интенсивности кавитации или при высокой механической стойкости металлов возможны проявления электрохимических эффектов. Так, в [12] показано, что эрозия твердых сталей происходит путем уноса оксидных пленок, которые перманентно восстанавливаются и являются менее стойкими, чем сам металл.

• 5.    Исходя из условий работы и конструктивных особенностей клапанной системы целесообразно изучение следующих мероприятий в плане поставленной задачи [15]:

  – изменение конструкции клапана;

  – изменение характеристики режима работы;

  – применение кавитационностойких материалов;

б )

Рис. 3. Распределение пузырьков воздуха по размерам: а) при V = 8 м/с, б) V = 10,5 м/с странственного его изменения – гидродинамическая кавитация) и называется, соответственно, вибрационной.

• - использование кавитационностойких покрытий (диффузионных, полученных различными методами напыления и т.п.);

  – комбинация из вышеперечисленных способов защиты от кавитационной эрозии.

• 6.    В качестве одного из основных и необходимых условий обеспечения снижения кавитационной эрозии следует отметить применение чистых от механических включений и по возможности дегазированных рабочих жидкостей.

• 7.    При выборе режима работы клапана следует учитывать возможность возникновения гидроудара.

• 8.    Наиболее перспективным с точки зрения безкавитационной работы или увеличения ресурса работы клапана представляется способ комбинации ряда мероприятий, который, в свою очередь, может привести к чрезмерному усложнению или удорожанию узла в целом. В этой связи следует сделать вариантный расчет технико-экономического обоснования выбранного мероприятия.

• 9.    Вследствие невозможности учета масштабного эффекта, обусловленного целым рядом факторов, модельные исследования нужно провести в условиях, близких к натурным, с использованием передовых современных практических и теоретических экспериментов (кристаллография, электронная микроскопия и т.п.).

• 10.    Масштабный эффект является причиной невозможности использовать результаты, полученные другими авторами для объектов, работающих в отличных от данных условиях.

Для расчета сложных трубопроводов успешно может быть использовано уравнение Н.А. Картвелишвили, полученное на основе уравнения Аллиеви:

^М     А/М     Э_Л,И

у^ + у.-^у.

С ( М М \ -h^—vd,

где y_t ^M и у " - напор в сечении M и N в момент времени t; v “ - скорость жидкости в сечении M , Ц = 2 L/C ; L - расстояние между сечениями M и N .

Запишем его в виде

• (1)    v⁽D    ?лЯ   nfo⁽²)   Г)⁽²⁾

^t+V + ^t    2У^—   Py^t    Xt — V у с где р = — , t - момент времени.

Уравнение (6) имеет три неизвестных величины. Для расчета гидравлического удара в системе уравнение (6) необходимо дополнить еще одним уравнением, аналогичным уравнению (6), и граничными условиями. Второе уравнение:

V(2) + v(2)   ?V(D -           O(2)

y t-з + У г-1 - 2y t-2 ^- P\^ t-1 - V_t -3 )

Здесь и далее верхние индексы относятся к номеру точки участка, а нижние – к рассматриваемому моменту времени. За шаг расчета приняты полфазы, т.е. v/ 2. Запись у^ означает, что рассматривается давление во втором сечении в момент, предшествующий рассматриваемому моменту t на _v/ 2.

Следует обратить внимание на то, что при выводе уравнений (6), (7) не были учтены потери напора на трение. Обычно бывает достаточно учесть потери энергии в граничных условиях.

В нашем случае, если не учитывать потери энергии, во время, когда регулирование не происходит, имеет место значительный рост погрешностей на каждом шаге расчета, что делает расчет бессмысленным. Это явление объясняется особенностями явления отражения волн от препятствий с постоянным нарастанием амплитуды колебаний.

Следовательно, для получения адекватных действительности результатов необходимо учитывать при расчете потери энергии на трение. В работе [1] найдены уравнения гидравлического удара с учетом потерь энергии. Гидравлический уклон принят функцией не только скорости движения жидкости, но и ее первой производной по времени vt = —. При установившемся течении у = у0; у = v0 = const. При неустановившемся течении у = у0 + Ду; у = v0 + Ду. В результате линеаризации гидравлический уклон принимается в виде i = Av, где i = av2; i = ^-, a2^

где A - среднее по времени и по длине значение; X - коэффициент гидравлического трения, принимается по гипотезе квазистационарности.

Уравнения удара с учетом трения будут иметь вид

• (2)      (2)/1                                                  У1

3^У

• У^ - У0(2) + в2 (уХ - У0(2)) + pVT+З^ [У^ - .0 - в2 ^1 - .о)] =

2e(yt-p1—уО1));    22

qW = Q,1a1(1+ ^yi-)Z^y^^ ;(io)

у        ² Ay *i /

Qt2) = Q*2«2(1 + ^^2^);

• y5w5 + v2W2 + 2v3w3 = 0;

  (2) y	(3) = y t ;	(13)
  v (3) yt-2	+y ;3, -2, ‘-4> =P 2 (g ‘3> -e ,(-2 );	(14)
  V (4) У г - 2	+ y t (4) - Zy ^ - ) = - p 2( Q t 4) - Q t-? );	(15)
  S p P ^	— ша р — ^ Tp = 0.	(16)

Уравнения (10)-(11) являются граничными условиями для клапанов; уравнение (16) – граничное условие для пресса. Уравнения (14)-(15) описывают процесс в трубе.

vx = 2(x2 - Xi)

71+^ c

; x₂, X j — ко о рдинаты сечения.

my      arog                     Л

в = е 2;m = ----;—; A = 2(1 + bg); a = —3—; b = 0,64.

1 + bg                   2dg

В результате решения системы (8)-(16) можно получить сведения о характере протекающих в гидросистеме нестационарных явлений.