KED - A Symmetric Key Algorithm for Secured Information Exchange Using Modulo 69

• I.    Introduction

  “Cryptography” is a science of secret writing[1].It is the art of protecting the information by transforming it into an unreadable format in which a message can be concealed from reader and only the intended recipient will be able to convert it into original text.Its main goal is to keep the data secure from unauthorized access. It is the science of encrypting and decrypting information, dates as far back as 1900 BC when a scribe in Egypt first used a derivation of the standard hieroglyphics of the day to communicate [2]. Every encryption and decryption process has two aspects: the algorithm and the key used for encryption and decryption [3].

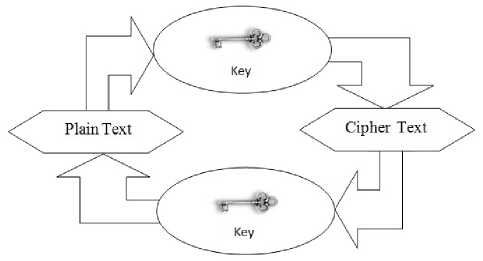
Figure.1: Cryptography

Encryption is the process of encoding plain text and converts it to non-readable format called cipher text. Decryption is the process of decoding cipher text converting it to plain text. There are two types of cryptography namely: Symmetric Key Cryptography and Asymmetric Key Cryptography. In symmetric key cryptography same key is used both for encryption as well as decryption process. Whereas in asymmetric key cryptography separate keys are used, one for encryption process and the other for decryption process.

The different goals of Cryptography are as follows :

a)    Confidentiality

Ensuring that no one can read the message except the intended receiver[4]. The information transmitted has to be accessed only by the authorized user.

b)    Authentication

The information received by any system has to check the identity of the sender that whether the information is arriving from an authorized person or false identity.

c)    Non-repudiation

Prevents sender or receiver from denying a message.A mechanism to prove that the sender really sent the message[4].

d)    Data Integrity

To ensure that data reaches in its original form to the receiver without any modification. Integrity is usually provided by message authentication codes or hashes.

e)    Access Control

Only the authorized parties are able to access the given information[5].

• A.    Brief history of cryptography and cryptanalysis

  The earliest form of cryptography was the simple writing of a message, as most people could not read (New World, 2007). In fact, the very word cryptography comes from the Greek words kryptos and graphein, which mean hidden and writing.[6]

Early cryptography was solely concerned with converting messages into unreadable groups of figures to protect the message’s content during the time the message was being carried from one place to another. In the modern era, cryptography has grown from basic message confidentiality to include some phases of message integrity checking, sender/receiver identity authentication, and digital signatures, among other things.[6]

Cryptography (or cryptology ; derived from Greek word kryptos meaning "hidden," and the verb grafo meaning "write" or legein meaning "to speak") is the study of message secrecy[7]. One of cryptography's primary purposes is hiding the meaning of messages, but not usually their existence. In modern times, cryptography is considered to be a branch of both mathematics and computer science, and is affiliated closely with information theory, computer security, and engineering. Cryptography is used in many applications encountered in everyday life; examples include security of ATM cards, computer passwords, and electronic commerce. It is also valuable for confidential governmental communications, on both domestic and international levels, especially during times of conflict.

Before the modern era, cryptography was concerned solely with message confidentiality (encryption) — conversion of messages from a comprehensible form into an incomprehensible one, and back again at the other end, rendering it unreadable by interceptors or eavesdroppers without secret knowledge (namely, the key needed for decryption of that message). In recent decades, the field has expanded beyond confidentiality concerns to include techniques for message integrity checking, sender/receiver identity authentication, digital signatures, interactive proofs, and secure computation, amongst others.

The earliest forms of secret writing required little more than a pen and paper, as most people could not read. An increase in literacy over time required actual cryptography. The main classical cipher types are transposition ciphers, which rearrange the order of letters in a message (e.g. 'help me' becomes 'ehpl em' in a trivially simple rearrangement scheme), and substitution ciphers, which systematically replace letters or groups of letters with other letters or groups of letters (e.g., 'fly at once' becomes 'gmz bu podf' by replacing each letter with the one following it in the alphabet). An early substitution cipher was the Caesar cipher, in which each letter in the plaintext was replaced by a letter some fixed number of positions further down the alphabet. It was named after Julius Caesar who is reported to have used it, with a shift of 3, to communicate with his generals during his military campaigns[6].

Extensive open academic research into cryptography is relatively recent — it began only in the mid-1970s with the public specification of DES (the Data Encryption Standard) by the NBS, the Diffie-Hellman paper, and the public release of the RSA algorithm. Since then, cryptography has become a widely used tool in communications, computer networks, and computer security generally[6]. The present security level of many modern cryptographic techniques is based on the difficulty of certain computational problems, such as the integer factorization problem or the discrete logarithm problem. In many cases, there are proofs that cryptographic techniques are secure if a certain computational problem cannot be solved efficiently[8].

As well as being aware of cryptographic history, cryptographic algorithm and system designers must also sensibly consider probable future developments in their designs. For instance, the continued improvements in computer processing power have increased the scope of brute-force attacks when specifying key lengths. The potential effects of quantum computing are already being considered by some cryptographic system designers; the announced imminence of small implementations of these machines is making the need for this preemptive caution fully explicit[9].

Cryptanalysis (from the Greek kryptos , "hidden", and analyein , "to loosen" or "to untie") is the art and science of analyzing information systems in order to study the hidden aspects of the systems[10]. Cryptanalysis is used to breach cryptographic security systems and gain access to the contents of encrypted messages, even if the cryptographic key is unknown.

In addition to mathematical analysis of cryptographic algorithms, cryptanalysis also includes the study of sidechannel attacks that do not target weaknesses in the cryptographic algorithms themselves, but instead exploit weaknesses in their implementation.Even though the goal has been the same, the methods and techniques of cryptanalysis have changed drastically through the history of cryptography, adapting to increasing cryptographic complexity, ranging from the pen-and-paper methods of the past, through machines like Bombes and Colossus computers at Bletchley Park in World War II, to the mathematically advanced computerized schemes of the present. Methods for breaking modern cryptosystems often involve solving carefully constructed problems in pure mathematics, the best-known being integer factorization.[10]

• B.    Types of cryptography

Cryptography is a process which is associated with scrambling plaintext (ordinary text, or clear text) into ciphertext (a process called encryption), then back again (known as decryption). There are several ways to classify the various algorithms. The most common types are i) Secret Key Cryptography which is also known as

Symmetric Key Cryptography and ii) Public Key Cryptography which is also known as Asymmetric Key Cryptography. [11]

Secret Key Cryptography

In secret key cryptography, a single key is used for both encryption and decryption. The sender uses the key to encrypt the plaintext and sends the ciphertext to the receiver. The receiver applies the same key to decrypt the message and recover the plaintext. Because a single key is used for both functions, secret key cryptography is also called symmetric encryption. With this form of cryptography, it is obvious that the key must be known to both the sender and the receiver; that, in fact, is the secret. The biggest difficulty with this approach, of course, is the distribution of the key.

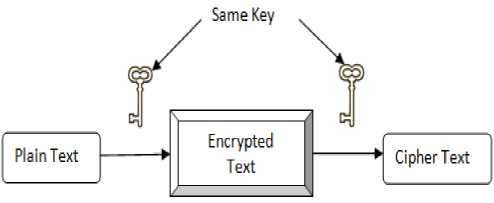
Figure.2: Secret Key Cryptography or Symmetric Key Cryptography

Public Key Cryptography

Public or asymmetric key cryptography consist of two keys or of key pairs: one private key and one public key. One is used for encryption and the other for decryption. The private key is private and is not to be shared with anyone. The owner of the key is responsible for securing it in such a manner that it will not be lost or compromised. On the other hand, the public key is just that, public. Public key cryptography intends for public keys to be accessible to all users. In fact, this is what makes the system strong. If a person can access anyone public key easily, usually via some form of directory service, then the two parties can communicate securely and with little effort, i.e. without a prior key distribution arrangement.[12]

Sender

Receiver

Receiver's Public Key

Receiver's Private Key

Plain Message

Plain Message

Encrypted Message

Figure.3: Public Key Cryptography or Asymmetric Key Cryptography

Many different cryptographic algorithms have been developed in recent past, some of which are the R.S.A , the D.E.S, which are looked upon as very safer for secure communication. But one thing common to all is the repetition of data values in the cipher coded text, or which in a different language might be called as patterns. An intelligent intruder might easily recognize these patterns and thus can generalize the coding algorithm after a deep analysis. This might pose a serious threat to data communication.

This paper is organized as follows. Section II gives a report on the related work. Proposed Work is explained in Section III. Implementation is explained in Section IV. The advantages of the proposed work is given in Section V. Section VI gives the conclusion of the paper.

• II.    RELATED WORK

Many cryptographic algorithms have already been proposed and implemented to provide security to the user that his/her message would remain safe at the time of communication over the web. But now a day’s hacking has become a common practice in society which made such cryptographic algorithms no longer safe. In this paper we have studied number of such symmetric key algorithms and selected one of them for reference in the proposed algorithm.

DES (Data Encryption Standard) was the first encryption standard to be recommended by NIST (National Institute of Standards and Technology) [13]. It was developed by an IBM team around 1974 and adopted as a national standard in 1997.

• •    DES is a 64-bit block cipher under 56-bit key.

• •    The algorithm processes with an initial permutation, sixteen rounds block cipher and a final permutation.

• •    DES application is very popular in commercial, military, and other domains in the last decades .

• •    Although the DES standard is public, the design criteria used are classified.

• •    There has been considerable controversy over the design, particularly in the choice of a 56-bit key

  Prakash Kuppuswamy, Dr.Saeed Q Y Al-Khalidi, in the year 2012 proposed an algorithm based on Modulo 37 [14].

• •    Uses two keys:      k1=positive

number,k2=negative number, find the inverse of both using modulo 37,giving k1’,k2’

• •    Assigning synthetic value for message A=1,B=2,….,Z=26,0=27,…,9=36,Space=37

• •    Encryption:Calculate with modulo 37,CT=(integer value*k1)mod37 , CT1=(CT*k2)mod37=Cipher Text

• •    Decryption: (CT1*k1’*k2’)mod37,

• •    In this algorithm only alphabets and numbers have been used.

Advance cryptography algorithm for improving data security By Vishwa gupta,Gajendra Singh ,Ravindra Gupta, 2012[15].

• •    Use random number for generating initial key.

• •    Block based substitution is method is used.

• •    Use 512 bit key size to encrypt which is 64 bytes and divide it into 4 blocks of 16-bytes.

• •    Apply XOR operation between the blocks.

• •    Resultant key block applied XOR operation with plain text 16 bytes, Apply circular shift with 3 values and then perform XOR operation again.

• •    Consumes large amount of memory space .

A Symmetric Key Cryptographic Algorithm By Ayushi,2010[16].

• •    Generate the ASCII value of the letter and corresponding binary value and reversing the binary

• •    Takes 4 digit divisor<=1000 and proposed two reverse operation for increasing security.

• •    There is no standard key generation method

• •    It is suitable for small amount of data

• •    Key size is small(<=8,can be predictable in just eight tries i.e., 1,2,3,…,8)

RDA Algortihm: Symmetric Key Algorithm By Dinesh Goyal,Vishal Srivastava ,2012[17].

• •    Proposed a new model by combining the Vignere Cipher Model and ECB(Electronic Code Book)

• •    VignereCipherModel:

• - Encryption: Ci=Pi+Ki (mod 26)

• - Decryption: Pi=Ci+Ki (mod 26)

• •    RDA Algorithm:

• -Encryption: Ci=Pi+Ki (mod 256)

• -Decryption: Pi=Ci+Ki (mod 256)

• •    Use a dynamic key pattern by shifting the key

matrix of times for m ‘rounds’ during the process of encryption and decryption so that every time new key is used.

• •    Key length is 1024

An Efficient Developed New Symmetric Key Cryptography Algorithm For Information Security By Suyash Verma, Rajnish Choubey, Roopali Soni, July 2012[18].

• •    It is a block cipher that divides data into blocks of equal length and then encrypts each block using a special mathematical set of functions known as key.

• •    Use 128 bit key size to encrypt which is arrange in a 4x4 matrix.

• •    16 byte plain text is also arrange in a 4x4

matrix

• •    Column shifting, Combination, permutation, column mixing, transposing and row mixing functions are applied in both the matrices.

A Modified Approach For Symmetric Key Cryptography Based On Blowfish Algorithm By Monika Agarwal, Pradeep Mishra, August 2012[19].

• •    It is a 64 bit block cipher with a variable key length.

• •    It consist of Key Expansion and data encryption.

• •    Operations such as XOR, S-Box are used.

• •    A random number range between 0 to 65535 is used.

• •    Key of the algorithm is based on the reference frame.

• •    Represent each character of plain text by another character.

• •    Grouping the modified plain text into blocks of eight characters.

• •    Convert each block into equivalent bit streams.

• •    Cipher block has been computed by placing position of bits of each character corresponding each position.

Multilevel Cryptography Technique Using Graceful Codes By K.Govinda, E.Sathiyamoorth, July 2011[21].

• •    White spaces are removed from the original string.

• •    Each character is then mapped into its equivalent ASCII value.

• •    The ASCII value is then encrypted into a set of random numbers by graceful code algorithm.

• •    The random numbers are then permuted.

• •    Decryption process is converting the permuted numbers to graceful code and then from graceful code to original numbers.

A New Symmetric-Key Block Ciphering Algorithm By Jamal N. Bani Salameh,2012[22]

• •    It encrypts a 64-bit plaintext to a 64-bit ciphertext in 8 rounds under the control of the key.

• •    The user key length and the number of rounds are variable.

• •    Various operation such as key mixing, S-boxes, Linear Transformation are applied.

• III.    Proposed work

In this paper, we propose a new algorithm which follows the symmetric key mechanism. Symmetric key cryptography is an encryption system in which the sender and receiver of a message share a single, common key that is used to encrypt and decrypt the message. Unlike asymmetric key cryptography, which utilizes two keys- a public key to encrypt messages and a private key to decrypt them. Symmetric key systems are simpler and faster. Symmetric key cryptography is sometimes called secret key cryptography.

Here we propose a new symmetric key algorithm called as KED (Key Encryption Decryption) and a new key generation method. The proposed algorithm is used for encryption and decryption process, using modulo69

and inverse modulo69. This algorithm is used for encryption and decryption, in which the same key is used both for encryption as well as decryption.

As we know that a message may consist of alphabets from A-Z, numbers from 0-9 and special characters such as +,-,%,< and so on. In this algorithm, firstly we assign integer values for each letters, digits and special characters. Alphabet ‘A’ is assign with integer value ‘1’, B=2, C=3,…..so on till Z=26. Next we assign the integer value 1=27, 2=28,…so on till 9=36. Space=37, !=38, “=39,…so on as shown below. The second part is the key generation process. By using the proposed key generation method we generate the second key i.e., K2. The first key i.e., K1 is an integer value taken from the user. The inverse modulo69 of K1 is generated and stored in ‘n1’. Hence using the keys K1, K2 and ‘n1’, the encryption and decryption process is carried out.

An inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y , then putting y into the inverse function g produces the output x , and vice versa. i.e., ƒ( x )= y , and g ( y )= x .[23]

A.    Integer Assigning

Here we assign integer values to the A-Z (26 alphabets), 0-9 numerics, space, and 32 other characters as shown below:

Table 1: INTEGER ASSIGNING

A	B	C	D	E	F	G	H	I
1	2	3	4	5	6	7	8	9
J	K	L	M	N	O	P	Q	R
10	11	12	13	14	15	16	17	18
S	T	U	V	W	X	Y	Z	0
19	20	21	22	23	24	25	26	27
1	2	3	4	5	6	7	8	9
28	29	30	31	32	33	34	35	36
space	!	“	#	$	%	&	‘	(
37	38	39	40	41	42	43	44	45
)	*	+	,	-	.	/		;
46	47	48	49	50	51	52	53	54
<	=	>	?	@	[	\	]	^
55	56	57	58	59	60	61	62	63
—	`	{	|	}	~
64	65	66	67	68	69

B.    Key Generation

• 1)    Generating ‘k2’, firstly user enters a key. The length of the key is stored in ‘kl’. Hence k2 is generated as follows:

К2= ( У ki 1 2' * kl * val) mod m

• 2)    Where,‘i’ is the position of each character in the key. ‘kl’ is the length of the key. ‘val’ is the integer value that has been assign to each character as shown in table 1 above.

• 3)    For ‘k1’, select any natural number say ‘k1’ where k1≠0 and must be relatively prime to ‘m’(i.e., ‘k1’ should not have factors in common with ‘m’).

• 4)    Find inverse modulo69 of ‘k1’ and store it in ‘n1’

C.    Encryption Process

• 1)    Firstly substitute or assign integer value for plain text.

• 2)    Multiply Synthetic value with first key i.e., k1.

• 3)    Now add the result from step2 above with second key i.e., k2.

• 4)    Then calculate with modulo69.

D.    Decryption Process

• 1)    Assign integer value for cipher text as given in Table1.

• 2)    Subtract ‘k2’ from above integer value.

• 3)    Multiply above result with inverse modulo69 of ‘k1’ i.e., ‘n1’.

• 4)    Finally calculate with modulo69.

• IV.    IMPLEMENTATION

• A.    Key Generation Process

• 1)    Let us suppose key enter by user is as follows: Key=2C%N

With positions, i= 0 1 2 3

keyLength, kl=4

Hence, k2= ( У k'12' * kl * val) mod 69

={( 2° * 4 * 29  )+(   21 * 4 *

3)+( 22 * 4 * 42)+( 23 * 4 * 14)} mod 69

= (116+24+672+448) mod 69 .     = 1260 mod 69

• . . k2 = 18

• 2)    Now select a natural number say, K1=5 Which is relatively prime to 69.

• 3)    Find the inverse of k1 denoted by n1=14(Verification: 5*14 moodulo 69=1)

• B.    Encryption

Let, Plain Text = SPRING2*13

Each characters in the plain text is assign with integer values as discussed above. The encryption process is as shown in Table 2 using keys k1 and k2.

Hence for the Plain Text = SPRING2*13

CipherText = ‘2”^S:Y)T3

Table 2 : ENCRYPTION

PlainText (PT)	Integer Value (V1)	V1*K1 (C1)	C1+K2 (C2)	C2 mod69	Cipher Text
S	19	95	113	44	‘
P	16	80	98	29	2
R	18	90	108	39	“
I	9	45	63	63	^
N	14	70	88	19	S
G	7	35	53	53
2	29	145	163	25	Y
*	47	235	253	46	)
1	28	140	158	20	T
3	30	150	168	30	3

• C.    Decryption

Now using k2 and n1(which is inverse mod69 of k1) , the cipher text is decrypted as follows :

Table 3 : DECRYPTION

Cipher Text (CT)	Integer Value (V2)	V2-K2 (P1)	P1*n1 (P2)	P2 mod69	Plain Text (PT)
‘	44	26	364	19	S
2	29	11	154	16	P
“	39	21	294	18	R
^	63	45	630	9	I
S	19	1	14	14	N
	53	35	490	7	G
Y	25	7	98	29	2
)	46	28	392	47	*
T	20	2	28	28	1
3	30	12	168	30	3

• V.    PROPOSED ALGORITHM

• A.    Algorithm for Key Generation and for finding inverse of K1.

  //Key Generation

for(int i=0;i

} key k2=d%69;

//Finding inverse for k1

K=69;

while (k1>0) { t = k/k1, y = k1;

k1 = k% y;

k = y;

y = z;

z = v - t*y;

v = y;

} v %= 69;

if (v<0)

{ v = (v+b)%69; //v=inverse of k1

}

• B.    Algorithm for Encryption

  //Encryption Algorithm for(i=0;i

n1=(num1*key1);

n2=(n1+k2)%69;

{ str1=""+n2;

if (entry.getValue().equals(str1))

encryptedmsg=encryptedmsg+ch;

}

}

}

• C.    Algorithm for Decryption

  //Decryption Algorithm

for(int m=0;m

{ str4=""+num3;

if (entry.getValue().equals(str4))

decryptedmsg= decryptedmsg +ch1;

}

}

}

• VI.    Advantages of Proposed Work

• 1)    It can be applied to a large amount of data.

• 2)    A proper key generation method is used.

• 3)    Two keys have been used and an inverse function which increases security.

• VII. CONCLUSION

Cryptography is used to achieve few goals like Confidentiality, Data integrity, Authentication etc. of the data which has been sent to the receiver from the sender. Now, in order to achieve these goals various cryptographic algorithms are developed by various people. The aim of this paper was to design and implement an algorithm to address this issue. Here we have used inverse modulo69 function and generated a key using the proposed key generation method. The proposed work has many advantages than the existing methods.