Кибернетический подход в анализе спортивных тренировочных нагрузок

Определение обратной связи, как первичного элемента искусственного интеллекта, ставит больше вопросов, чем ответов. Как постулат, умозрительно можно принять, но какие качественные и какие количественные признаки способствуют её возникновению, мы не знаем.

При рассмотрении разрабатываемых в настоящее время моделей биосистем с позиций теории управления, и имеющих случай многосвязной системы. Выбранные переменные данных систем могут играть роль регулируемого или управляемого сигнала в системе управления: это концентрации веществ -глюкозы, углекислоты, гормонов - или переменные артериального давления, или переменные кровотока через орган. Интересы других моделей представляют темпы изменения переменных, описывающих саму биосистему [7, 8].

Возможно, для открытых биологических систем изменение гомеостатического равновесия на различных уровнях морфофункциональной модели [1] ведет к изменению противоречивых количественных соотношений между взаимозависимыми регуляторами [2]. Существование антагонистических противоречий в свою очередь ведет к селективному отбору [11] нужного регулятора из близлежащих иерархических структур, вызывая в них активные или пассивные механизмы траты энергетических веществ [7].

Выявление зависимых активных и пассивных тенденций в энергетическом обмене по регуляции гомеостатического равновесия еще не означает, что эти процессы не обратимы. Двойственность чисел в селекции между ак-тивно-возрастающей и активно-убывающей тенденцией позволяет сделать выбор в пользу более активной физиологической адаптации. Селективные двоичные функции 22 от n переменных представляют другую конструкцию накопительного итога для активных и пассивных тенденций в динамической иерархии временного ряда [12].

Управление активными и пассивными энергетическими окислительными и восстановительными процессами [7], может быть определено смешанным математическим моделированием параметров с использованием аналоговых, цифровых или физических моделей [8].

На рисунок 1 показатель W0 - представляет планируемые в спорте параметры нагрузки в определенном микроцикле; W - показатель баланса активных и пассивных накопительных структур; € - координаты возрастающих и убывающих тенденций в переменных накопительного итога; Z и X - селективные двоичные функции 22 от n переменных; V - неконтролируемые внешние воздействия; Y – состояние физиологической адаптации [7, 10].

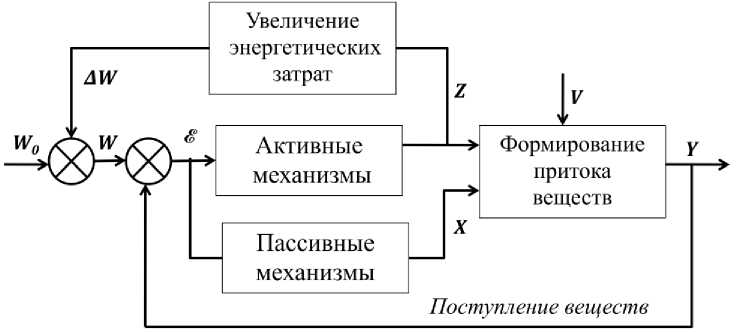
Рис. 1. Структуры переменных для открытой системы

Каждый вид спорта представляет определенную морфофункциональную модель, в которой на первом месте стоит развитие главных, а затем второстепенных двигательных качеств [15]. В циклических видах, где нагрузка выполняется продолжительное время, главным является развитие выносливости, а на коротких соревновательных отрезках времени – требуется развитие быстроты. В игровых видах спорта уделяют больше внимания развитию координации движений. На коротких соревновательных дистанциях в гребле, велоспорте, конькобежном спорте в большей степени уделяют внимание развитию быстрой силы, если же соревновательная дистанция более протяженная, то уделяют больше внимания развитию силовой выносливости [9, 10].

Тренирующий эффект суперкомпенсации в формировании уровня повышенной двигательной активности достигается за счет возрастающих специфических воздействий, ко- торые должны быть на порядок выше воздействий предыдущих. Явление суперкомпенсации графически представляет трату энергетических ресурсов организма убывающей кривой, а её подъем – восстановление потраченных ресурсов с незначительной компенсацией. Повторяющиеся нагрузки в точке возрастающей компенсации представляют в тренировочном процессе динамически растущий волнообразный процесс [14].

Тренировка подобранными развивающими упражнениями приводит к формированию в организме морфофункциональной физиологической модели [1]. Тренирующие нагрузки, заданные в виде взаимозаменяемых накопительных кумулятивных кривых (рис. 2), могут влиять на темпы более быстрого или более медленного восстановления. Целевые программы выбора таких структур, в итоге, представляют программу успешного управления тренировочным процессом [10].

Рис. 2. Активная и пассивная формы накопительного итога

Показатель мощности нагрузки в плане подготовки может находится в разных структурах накопительного итога (рис. 2). Одновременное их планирование для различных мышечных групп в результате дает возможность совместить работу для одних и отдых для других (рис. 3).

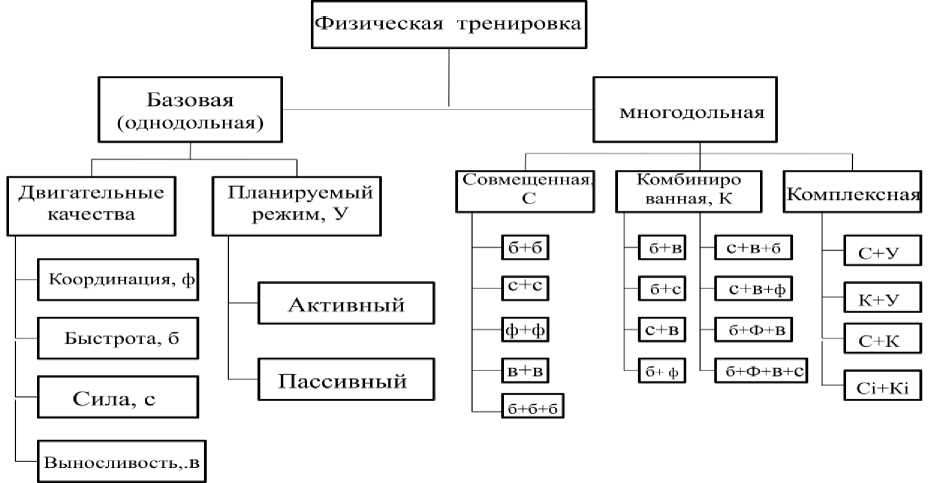
Рис. 3. Классификационная диаграмма [19]

Физическая работа вызывает определен-   ской работы и мощности определяют по сле- ную напряженность в деятельности различ-   дующим формулам:

ных систем организма. Значения динамиче-

A =F ••S.  N = - или N =     N = F-V.

t

Где А - совершаемая работа (Дж, кгм); N -мощность (Вт, кгм/мин); F - усилие (кг); S -расстояние (м); V - скорость (м/с); t - продолжительность работы (мин,с).

Величину статической работы, например удержание туловища на одной ноге в полу-приседе, находят без показателя S :

A = F• t.

Указанные выше параметры нагрузки широко используются при описании того или а затем из общего ряда амплитуд в отдельные динамические ряды последовательно выбираются положительные (∆+) и отрицательные (А--) амплитуды. Накопительные свойства активных и пассивных долевых тенденций (ДТ) в динамике положительных и отрицательных амплитуд, выбранных из общего ряда, представлены на рисунке 2.

Данные значения в долевых тенденциях дает возможность установить связь между развитием быстроты, силы, и выносливости (рис. 3), а также дают возможность устано- t иного упражнения [8]. Но, когда возникает необходимость описать накопительный эффект объема и интенсивности за временной период, то более объективным показателем взаимозависимых изменений будет долевая тенденция [10]. Для её определения вначале выделяются амплитуды прироста между последовательными интервалами планируемых показателей:

А ± = (C i+1 -С),                                  (1)

вить связь между развитием физиологических параметров тех или иных систем организма.

В физическом макромире и в технологии производства и управления в подавляющем большинстве случаев динамические зависимости сопровождаются не дискретными, а сопутствующими континуальными пространственно-временными процессами [1, 7]. Поэтому в континуальной области векторных пространств каждая физическая ситуация и класс объектов проектирования физических нагрузок требует использования или разра- ботки своего логико-алгебраического исчисления [10, 13].

Противоречивые же зависимости, или альтернативные (0 и 1), должны иметь степень уверенности в справедливости этих зависимостей. Тогда, с помощью весов противоречивые зависимости переводятся в зависимости вероятностные [В.М. Глушков,1974]. С весами противоречий, соответствующих для p и q будет (p = m/n ), где p - доля чисел, являющихся обладателями данного признака, а q -доля чисел, не обладающих данным признаком [А.Б. Гусынин, 2002].

В этом случае истинность высказывания показателей системной подготовки может определяться функциями булевы алгебры, где весы взаимозависимых влияний между логическими операциями будут зависеть от конечного числа двоичных переменных. А способность принимать значения (A⁺ ∧ B^–) или (A + V B ) будет подаваться со значениями и связями входящих в них высказываний [16].

Материал и методы исследования. Для исследований были взяты тренировочные планы МСМК Косьяненко С., которые ис- пользовались им в 2013 году при подготовке к Всероссийскому турниру на призы губернатора Калужской области [4].

Для изучения и создания модели структурных характеристик в тенденциях планируемых показателей тренировочной нагрузки использовалась: классификационная диаграмма долевых зависимостей (рис. 3), холистический подход в [12], четырехмерная измерительная модель ДТ и таблица связей логических высказываний [13]. В представленной литературе:

Показатель долевой тенденции (ДТ) определяется из условной доли вероятности между показателем динамики стандартного плана и динамикой вероятности исследуемого ряда [5, 13].

Иерархия тенденций колеблемости в динамике планируемого ряда тренировочной нагрузки выявлялась применением холистического подхода (рис. 4). Вначале данным методом выделяются ряды, затем в этих рядах определяются ДТ на 1-м, 2-м и 3-м иерархическом уровне [11]. Дальнейшее разделение может идти до 9-го уровня [12].

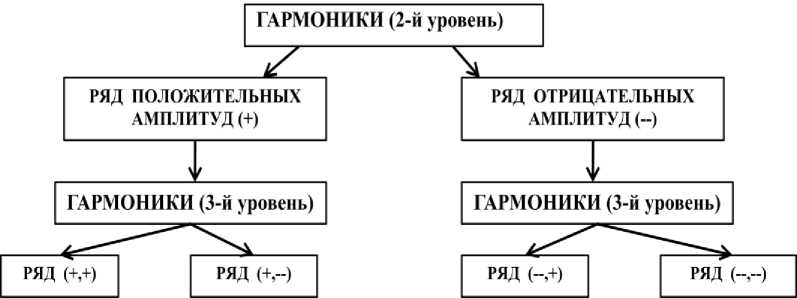
Рис. 4. Иерархические уровни в динамике исследуемого ряда

Четырехмерная измерительная модель ДТ (рис. 5) создается после удаления вычитанием данных прогрессии динамики стандартного плана (формула-3), которая на (рис. 2) представляет равномерно возрастающую прямую линию, а выпуклая и прогнутая дуги, соответственно, формы активного и пассивного накопления. После удаления стандарта происходит инверсия, в результате происходит конформное преобразование Эвклидовой плоскости, что создает условия для перехода динамического процесса из одной плоскости в другую. В разделенной плоскости двухмерного пространства М, стандарт (pst) принимает позицию горизонтальной разделительной линии (0), разделяющей плоскость на активную (0Р+) и пассивную (0Р) зоны. При переходе исследуемого ряда в одну из зон он отражает процесс активного (С), или пассивного (D) накопления [13].

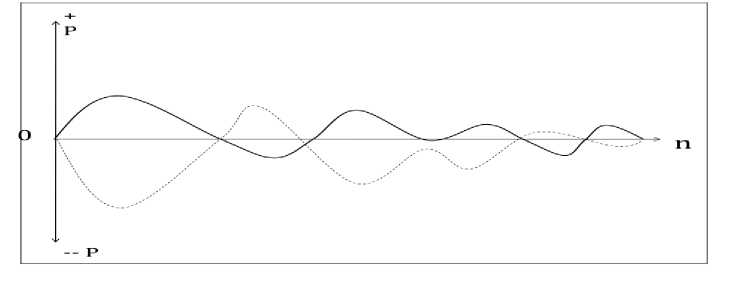
Рис. 4. Четырехмерная пространственно-временная модель.

В альтернативной динамике для выделенного в иерархии (рис. 4) динамического ряда возрастающих амплитуд (А+) и динамического ряда убывающих амплитуд (В–) двухкомпонентная зависимость в тенденциях формы и в тенденциях зависимых противоречий представляет значение и связи логических высказываний. Зависимость между сложным и простым высказываниями представлено таблицей, где в правой части приведены возможные значения аргументов простых высказываний (A+, B–), а в левой части – значения функции сложного высказывания (C,D). Представленные в таблице формы исследуемого динамического процесса можно представить двоичной функцией 22 от n переменных. Используемые простейшие операции над высказываниями состоят из конъюнкции (A+ Л B ), дизъюнкции (A + У B ) и отрицания (инверсия) [16].

Таблица 1. Определение форм антагонистических взаимодействий в тенденциях зависимых противоречий

Накопительная вариабельность		Итог накопления		зависимости
		активный	пассивный	возрастающие	убывающие
1	Активно-возрастающая	C		A+
2	Пассивно-возрастающая		D	A+
3	Активно-убывающая	C			B–
4	Пассивно-убывающая		D		B–

Для вычисления различных показателей долевой тенденции (ДТ) в программе Excel составлена двумерная вычислительная таблица [6], которая позволяет значительно сокращать время обработки данных, если учесть, что численность показателей временного ряда может быть больше n > 500.

Схема последовательных вычислений в программе Excel :

∆± = Ci+1 – Ci. Выделение амплитуд(1)

Bi= (pi + pi+1) + п /ArccosZa Доля прироста(2)

By= Bi — hst .     Выбор стандарта(3)

ДУУij = Ву + Ву+1. Доля условного участия(4)

ДУАij = ДУУij / n – 1. Доля активности(5)

КЕ1,2 = ДУУ * ДУА. Кумулятивная емкость гармоник(6)

РДС = 1/ [√ Σ(ДУУi – ДУУj)2/n – 1]. Резерв динам. сопряжения(7)

Вх = √ (В± – ОРинт)2. Выбор тенденции гармоники(8)

НВх= Вх + Вх+1.   Накопительная вариабельность(9)

КЕ3 = ДУУвх * ДУАвх   Кумулятивная емкость 3-го уровня (±)(10)

ДСА=[(НВi + НВj)/НВj]–[(НВi + НВj)/НВi].  Диапазон(11)

Р = limm/n. Вероятность исхода(12)

Результаты исследований и их обсужде- тренировочного плана нагрузки [4] поднима ние. На рисунке 5 представлена динамика емой гири (рывок) в тоннах за определенное

количество раз (рис. 5, график величин «натуральные»). Вес гири и количество подъемов в разные тренировочные дни менялся. Амплитуды подъемов и снижений нагрузки были выделены из общего ряда (рис. 5, гармоника) динамики (см. формулу-1) и представлены графиком (гармоника).

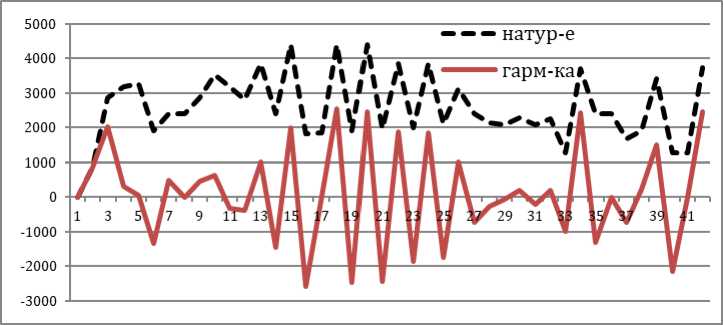
Рис. 5. Тоннаж поднимаемой гири рывком [4]

Как мы видим из графика динамика натуральных величин и гармоники имеет структурную схожесть. Гармоника отличается наличием положительных и отрицательных величин. Эти амплитуды значительно больше амплитуд натурального ряда. Выбранные из временного ряда плана тренировки в отдельные ряды положительные и отрицательные амплитуды представляют подструктуры трендовой компоненты [3]. Измеренные периодические колебания в рядах динамики представляют положительные и отрицательные вариации колеблемости [13]. Полиномиальные уравнения показывают на различный характер тенденций в выбранных положительных и отрицательных рядах (рис. 6).

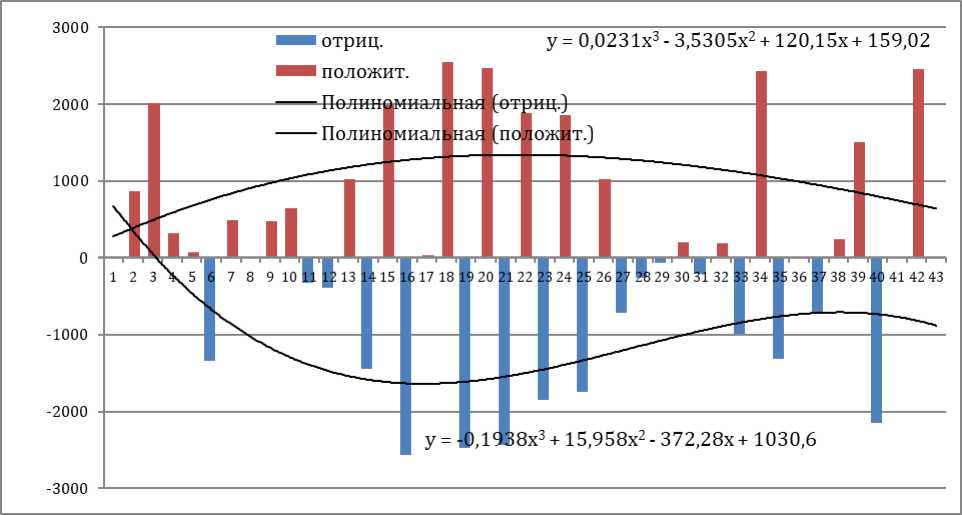
Рис. 6.

Показатель мощности (N) каждого ряда N = ^^ может быть выражен в кг^м/мин. Все показатели сопряжены, что не дает возможности определить суммарную мощность выпол- ненных упражнений на силу или выносливость в плане подготовки. На практике смещения в тренировке в сторону силы или выносливости, без учета показателя t, может идти при использовании повторного метода (в плане это серии) или метода «фартлек». В плане итоговой подготовки развитие силы и выносливости может быть отражено [10] в структурах накопительного итога долевых тенденций (формула 2-4).

На рисунке 7 мы видим, что динамика долевой тенденции (ДТ) тренда (НАТ) в упражнении – рывок плавно возрастает. Тогда как долевая тенденция гармоники (ОР) позволяет выявить структуры накопительного итога.

Вначале ряда ДТ имела пассивно-возрастающую накопительную структуру (20я тренировка), а затем была преобразована (32-я тренировка) в активно-возрастающую структуру (см. табл. 1). Примерно до 20 дня спортсмен в тренировках уделял больше внимания развитию выносливости. В дальнейшем в тренировках уделялось больше режиму силы, вес гири и количество ее подъемов стало резко возрастать.

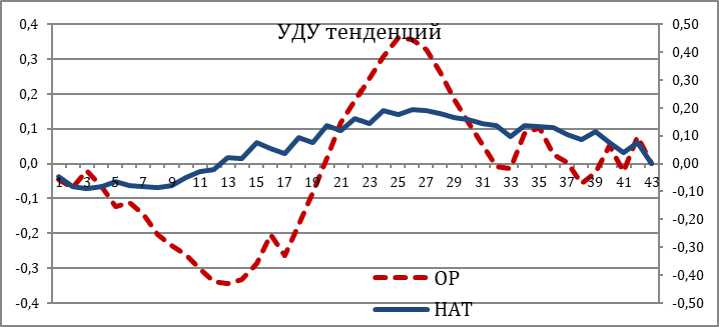
Рис. 7. Тоннаж тренировочного плана в долевых тенденциях

Данный подход мог перевести к переутомлению. В итоге на 36 занятии (рис. 7) спортсмен в плане отметил боли в мышцах спины. В результате план подготовки к Всероссийскому турниру в Калуге был сорван. На соревнованиях был показан результат контрольной тренировки 2-х недельной давности.

Выбранные из гармоники в отдельные ряды (рис. 8) показатели положительных (+) и отрицательных приростов (–) в тоннаже нагрузки дают тенденции структур накопительного итога ДТ (формула 2-4), которые зависят от тенденции ряда гармоники (рис. 8,а), ряд – ОР). Удаление этой тенденции (формула 8) выявляет противоречия в структурах между выбранными амплитудными рядами (рис. 8,б)). Эти ряды представляют двоичные функции состоящие из простых (А+, B–) и сложных высказываний (С,D) (см. табл. 1).

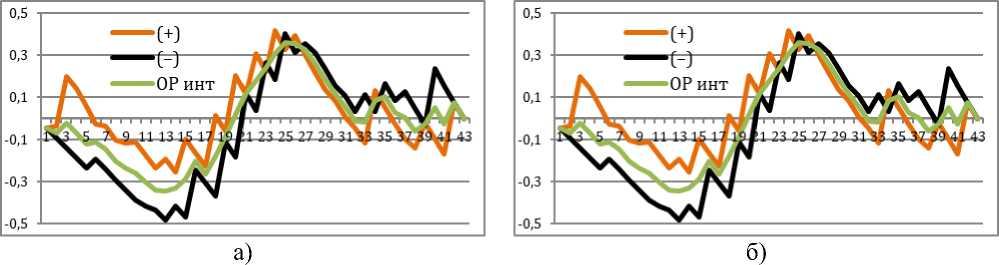
Рис. 8. Весы противоречивых зависимостей: а) – до удаления гармоники; б) – после удаления гармоники

Конъюнкция высказываний (A+, B–) для выделенных рядов, имеющих зависимость от гармоники, имеют пассивную (D) и активную (С) возрастающую структуры накопительного итога (рис. 8,а)). После удаления тенденции гармоники (формула 8) между рядами выявляется противоречивые взаимозависимости. До 25-го тренировочного дня ряд из положи- тельных амплитуд (рис. 8,б)) представляет конъюнкцию активно-возрастающего высказывания (C∧ A+). А ряд из отрицательных амплитуд представляет пассивно-убывающее высказывание (D∧B–).

После 25-й тренировки произошла взаимозамена: для положительных амплитуд нагрузка стала пассивно возрастать - (D∧ A+), а для отрицательных амплитуд стала активно-убывающей (C∧ B–). Таким образом, отличительные свойства структур накопления до и после 25-го занятия отображают пересечение в нулевом векторе двух пространств, каждое из которых является подпространством гармоники [16]:

(D ∨ C) ∧ B^– ≥ (D ∧ B^–) ∨ (C ∧ B^–);

(C ∨ D) ∧ A⁺ ≥ (С ∧ A⁺) ∨ (D ∧ A⁺).

Пересечение элементов D∧C или их объединение D∨С в конформно преобразованной Эвклидовой плоскости (Рис.4) способствуют переходу динамической структуры для показателя В– (или показателя А+) из одной плос- кости в другую [16]. Данная инверсия отражает антагонизм в структурах, в результате которой на весах противоречивых зависимостей [2] выявляется доминирующий антагонист (табл. 2).

Таблица 2. 2-й уровень иерархии. Значения противоречивых взаимозависимостейв структурах положительных ((C∨ D)∧ A+) и отрицательных ((D∨ C)∧ B–) рядов.

Зависимости	(C ∨ D) ∧ A+	(D ∨ C) ∧ B–
Р	0,51	0,49
КЕ 2	0,07	– 0,03
ДСА НВ	1,97	2,03
РДС	0,523	0,638

В таблице 2 показатель Р = lim m/n представляет вероятность исхода, величина 0,51 говорит о доминировании процесса увеличения нагрузки за весь тренировочный период. Показатель 0,49 говорит о доле уменьшения нагрузки в плане, возможно связанной с получением суперкомпенсации в периоде восстановления.

Показатель КЕ 2 = ДУУ * ДУА характеризует итог процесса накопления в возрастающей (0,07) и убывающей нагрузке (-0,03). Показатели КЕ 2 (рис. 9) характеризуют структуры накопления, в которых так же выявляется доминирующий антагонист ( А⁺ ).

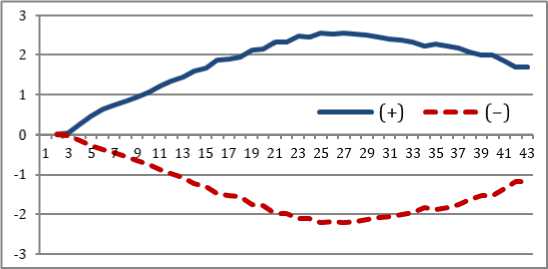
Рис. 9. Структуры условного долевого участия

Показатель ДСА=[(НВ i + НВ j )/НВ j ]–[(НВ i + НВ j )/НВ i ] характеризует диапазон изменчивости ( НВ ) в структурах, что позволяет сравнивать разные тренировочные планы.

Показатель РДС = 1/ [√ Σ(ДУУi – ДУУj)2/n – 1] характеризует резерв динамического со- пряжения между выбранным рядом и структурой гармоники их которой они были выбраны. Показатель положительных приростов 0,523 характеризует (табл. 2) большее приближение к динамике тренировочного плана и меньший вариационный разброс.

В зависимости от выбранного вида спорта классификационная диаграмма (рис. 3) помогает определить в какую группу (совмещенная, комбинированная) развития двигательных качеств (быстрота, …, выносливость) входят те или иные мышечные группы. В тренировочном занятии одна группа мышц может выполняться нагрузку по активному плану, другая мышечная группа – по пассивному плану (см. рис. 3, комплексная: С+У и К+У). Такой подход дает возможность дозировать работу для одних мышц и отдых для других.

В отличие от обычного вычисления тенденций тренда и дисперсии трендовых компонент [7]. В оценках динамики нагрузки вместо дисперсии вычисляются долевые тенденции трендовых компонент и их накопительные структуры [13]. Булевы алгебры позволяют в этих структурах определить алгоритм событий структурной конфигурации и описать динамику структурных изменений [16].

Выводы. Физическая тренировка организ- бальных перестроек различных систем управления гомеостатическим равновесием, которая позволяет сформировать свои отличительные морфофункциональные модели.

В отличие от обычного статистического вычисления тенденций тренда и тенденции трендовых компонент. В оценках динамики задаваемой нагрузки долевые тенденции и их накопительные структуры позволяют создавать математические модели и оценивать успешность их освоения. А сравнение тренирующей модели и модели физиологических реакций дает возможность управлять тренировочным процессом.

Противоречивые высказывания в булевах алгебры в планировании физической нагрузки замыкаются на весах противоречивых зависимостей. Используемый в данной работе подход высказываний и противоречий позволяет в анализе выполненной тренировочной программы определить доминирующий антагонист и выявить моменты критического утомления.

ма является селективным регулятором гло- пекты теории управления. – 1976. – Вып. 8. – С. 23-24.