Кинематическая операция построения геометрических тел в точечном исчислении
Автор: Конопацкий Евгений Викторович, Бездитный Андрей Александрович
Рубрика: Инженерная геометрия и компьютерная графика. Цифровая поддержка жизненного цикла изделий
Статья в выпуске: 3 т.22, 2022 года.
Бесплатный доступ
Данная статья продолжает цикл работ авторов по разработке математического аппарата моделирования геометрических тел в точечном исчислении и посвящена описанию кинематической операции, реализованной с помощью метода подвижного симплекса. Принципы моделирования геометрических тел в точечном исчислении основаны на концепции их представления в виде трёхпараметрического множества точек, принадлежащих трёхмерному пространству. Тогда задача моделирования будет состоять из двух частей: определение направляющей траектории движения плоского симплекса в пространстве и определение образующей замкнутой области в плоскости подвижного симплекса. Вместо замкнутой области можно использовать две кривые, ограничивающие некоторую область, или направляющую кривую, которая имеет стенку постоянной толщины. В качестве примера приведено описание процесса моделирования геометрических тел с плоскостью параллелизма, включая вычислительный алгоритм его формирования в виде последовательности параметрических уравнений. В результате получены геометрические и компьютерные модели тел с образующей в виде окружности заданного радиуса и с образующей в виде замкнутой кривой типа «синусоида». Приведенные в статье приёмы параметризации геометрических объектов и их аналитического описания в точечном исчислении могут найти широкое применение как эффективные инструменты современных систем твердотельного моделирования и автоматизированного проектирования. Также предложена идея определения эквидистантных кривых с помощью точечной формулы параллельного переноса, расширяющая возможности существующих инструментов геометрического моделирования.
Кинематическая операция, геометрическое тело, точечное исчисление, метод подвижного симплекса, параллельный перенос, эквидистанта, замкнутая кривая
Короткий адрес: https://sciup.org/147238614
IDR: 147238614 | УДК: 004.925.8 | DOI: 10.14529/build220309
Текст научной статьи Кинематическая операция построения геометрических тел в точечном исчислении
Кинематический метод моделирования геометрических объектов имеет большое значение в различных областях машиностроения, строительства и архитектуры. Он используется для решения широкого круга инженерных задач. Например, для математического профилирования червячного инструмента [1], моделирования поверхностей элементов червячной передачи [2], моделирования поверхностей при обработке концевой фрезой [3], конструирования архитектурных покрытий [4], параметрического описания поверхности фигуры человека [5] и т. д. А необходимость его аналитической и компьютерной реализации для нужд производства явилось катализатором проведения многих исследований в области инженерной геометрии и компьютерной графики, направленных на решение этой научной проблемы и разработки различных способов её решения. Среди этих исследований можно выделить две категории работ: работы, направленные на разработку и усовершенствование графического и математического аппарата кинематического моделирования геометрических объектов [6–11], и работы, направленные на использование существующих систем автоматизи-
рованного проектирования и компьютерной графики для решения инженерных задач проектирования и в учебном процессе [12–14].
Аналогом кинематической операции в точечном исчислении [15, 16] является метод подвижного симплекса, который представляет собой обобщение кинематического метода на многомерное пространство за счёт параметризации геометрических объектов в точечном исчислении. Благодаря этому обобщению он получил значительное развитие не только как инструмент формообразования различных поверхностей технических и архитектурных форм, но и как один из базовых методов геометрической теории многомерной интерполяции и аппроксимации [17–19] для моделирования многофакторных процессов и явлений. Также метод подвижного симплекса является основой для реализации кинематической операции твердотельного геометрического моделирования по аналогии с [20]. В отличие от существующих подходов к твердотельному моделированию, которые сводятся к определению полой оболочки, в работах [21, 22] предложен и показан на примерах метод моделирования геометрических тел в виде трёхпараметрического множества точек, принадлежащих
Инженерная геометрия и компьютерная графика…
трёхмерному пространству. При этом получены точечные и параметрические уравнения геометрических тел, заполненных точками. Для дальнейшего развития предложенного подхода к твердотельному геометрическому моделированию необходимо разработать основные инструменты определения геометрических тел в точечном исчислении, одним из которых является кинематическая операция, реализованная с помощью метода подвижного симплекса.
Метод
Концепция метода подвижного симплекса заключается в том, что геометрический объект определяется в пространстве симплекса, который сам движется в пространстве. Такое движение может носить сложный характер, когда система, в которой определяется подвижный симплекс, также подвижна. В зависимости от количества точек симплекса, имеющих свободную траекторию движения, выделяют различные его виды. Например, частным случаем реализации метода подвижного симплекса является операция вращения. Вращение может происходить вокруг оси, когда фиксируются две точки из трёх точек подвижного симплекса, и вокруг точки, когда фиксируется одна точка из трёх. Подобное вращение свойственно плоскому симплексу. Вместе с тем, обобщая на многомерное пространство можно получить вращение симплекса трёхмерного пространства вокруг плоскости и т. д.
Рассмотрим одно из возможных приложений метода подвижного симплекса для определения геометрических тел в точечном исчислении. Пусть в декартовом симплексе OE i E 2 E 3 (рис. 1) заданы три линии:
P = ( E1 - O) p1 (и) + (E2 - O) q1 (и) + (E3 - O) r (и ) + O,
Q = (E1 - O) Р2 (u) + (E2 - O) q2 (u) + (E3 - O) r2 (u) + O, R = ( E1 - O) p 3 (и) + (E2 - O) q 3 (и) + (E3 - O) r3 (и) + O, где pi (и), qi (и), ri( и) - любые непрерывные и дифференцируемые функции от параметра и е[0;1].
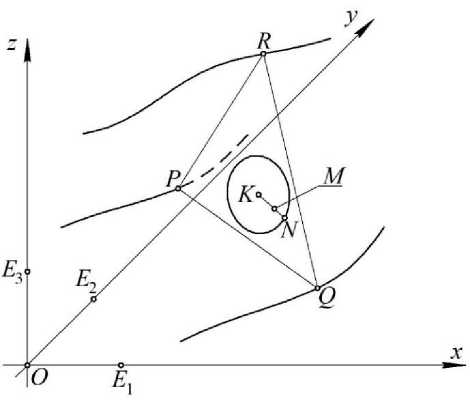
Рис. 1. Геометрическая схема для описания кинематической операции твердотельного моделирования в точечном исчислении
Текущие точки P , Q и R формируют плоский симплекс, который движется за счёт их перемещения в пространстве. Движение подвижного симплекса PQR по направляющим линиям согласовано с помощью одинакового параметра и .
Зададим в симплексе PQR замкнутую область, заполненную точками, как показано на рис. 1. Заполнение этой области точками обеспечивается за счёт двойного движения. Во-первых, текущая точка M своим движением заполняет симплекс одномерного пространства - отрезок KN : M = ( N - K ) w + K , где w е [ 0;1 ] . Во-вторых, симплекс KN также является подвижным в пределах плоского симплекса PQR . Его движение может носить разный характер. Например, это может быть вращение отрезка KN вокруг точки K , который определяется с помощью параметра v е [ 0;2 п ] :
, _ r sin (v- v) , _ rsinv
N = ( P - K) (I---)+(Q - K) ---•----+ K, (1)
PK| sin Y QK| sin Y где r = IKNl - радиус окружности;
IPK=V(xp - xk )2 +(у? - Ук )2+(zp - zk )2;
IQK = J(xQ - xK )2 + (yQ - Ук )2 + (zQ - zK )2 ;
y = Z PKQ (см. рис. 1).
Угол у определяется через координаты точек. Например, через метрический оператор трёх точек:
K
^ PQ cos Y =
PK QK
(xp - xK )(xQ -xK ) + (Ур - Ук)(yQ - Ук ) + (zp - zK )(zQ - zK )
PK QK
Таким образом, формируется твердотельный геометрический объект, который определяется тремя параметрами: u , v и w .
На рис. 1 показан общий случай, при котором движение симплекса PQR определяется тремя произвольными линиями, но в качестве частных случаев можно рассмотреть использование точечной формулы параллельного переноса для построения тел с плоскостью параллелизма. В качестве такой плоскости может выступать и плоскость сечения. Также, используя метрический оператор трёх точек и операцию определения точки выхода из плоскости, которые являются аналогами скалярного и векторного произведения векторов в точечном исчислении, можно определять траектории движения, перпендикулярные сечению.
Заполнение точками пространства в симплексе PQR можно осуществлять и другими способами (рис. 2). Форма замкнутого контура может носить произвольный характер. Это может быть непрерывная или составная кривая, как показано на рис. 1, а может быть некоторая ломаная (рис. 2а) или их комбинация. В любом случае форма замкнутого контура определяет движение отрезка KN в симплексе PQR .
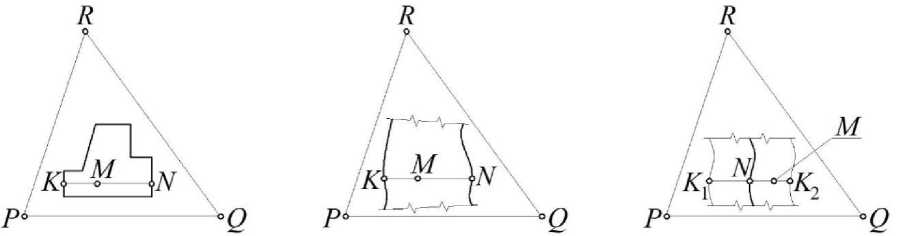
а) б) в)
Рис. 2. Геометрическая схема заполнения плоскости подвижного симплекса точками: а) замкнутый контур;б) контур произвольной формы, образованный двумя линиями; в) линия произвольной формы со стенкой постоянной толщины
Также возможно построение твердотельной модели и при отсутствии замкнутого контура. В этом случае тело может определяться произвольным движением точек K и N (рис. 2б), определяющих своим движением две линии - границы тела, формирующие незакономерную стенку. Эту стенку можно задавать постоянной толщины | K j K 21 = 8 (рис. 2в). Тогда достаточно одной направляющей линии для её определения из условия, что эта линия будет проходить, например, посередине стенки:
M = ( K 2 - K 1 ) w + K 1 = 2 w ( N - K 1 ) + K 1 . (2)
Решение задачи формирования линии произвольной формы со стенкой постоянной толщины сводится к решению другой задачи - построение эквидистанты кривой [23, 24] и будет более подробно рассмотрено ниже.
Обратим внимание, что контур произвольной формы можно также задать одной линией, по аналогии с рис. 2в, и функцией изменения длины отрезка 8 = 8 ( v ) , заполняющего пространство внутри тела точками.
Результаты и обсуждения
Рассмотрим в качестве примера моделирование геометрического тела с плоскостью параллелизма ABC (рис. 3).
Инженерная геометрия и компьютерная графика…
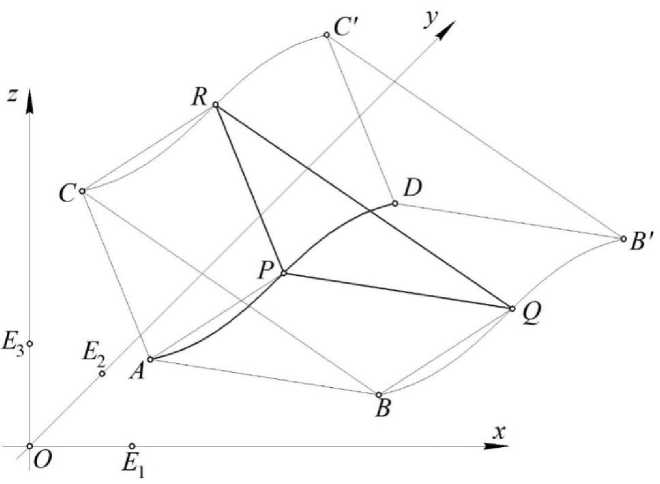
Рис. 3. Геометрическая схема определения подвижного симплекса PQR
Пусть в симплексе ABCD (см. рис. 3) задана линия текущей точкой P . Она может быть как плоской, так и пространственной. В качестве примера рассмотрим пространственную кривую, которая определяется трансцендентным точечным уравнением:
P = ( A — D ) u 3 +(B — D ) U3 +(C — D )sin (u 3 + u 2 ) + D, где u = 1- u - дополнение параметра u e[0;1] до 1.
Обратим внимание, что для определения локального симплекса ABCD в глобальном декартовом OE 1 E 2 E 3 достаточно ввести соответствующие координаты точек симплекса. Таким образом, в глобальном декартовом симплексе будут переопределены все геометрические объекты в симплексе ABCD .
Выполнив покоординатный расчёт, получим систему однотипных параметрических уравнений:
x P = ( x A
—
x D ) u 3 +( x B
—
x D ) u 3 + ( x c
—
xD
) sin ( u 3 + u 2 )
+ x D
‘ Ур = ( Уа
—
y D ) u 3 +( У в
—
У о ) u 3 +
( У c — У о ) sin ( u 3 + u 2 )
+ yD .
zP = ( zA
—
zD
) u 3 + ( zB
—
zD
) u 3 + ( z C
—
zD
) sin ( u 3 + u 2 )
+ zD
Точки Q и R подвижного
PQR симплекса PQR определим с помощью точечной формулы парал- лельного переноса:
= xP + xB — xA
x Q
Q = P + B - A ^1УQ = Ур + Ув - Уа , xR = xP + xc — xA
R = P + C - A ^ 1 yR = yр + Ус - УА .
zQ = zP + zB zA zR = zP + zC - zA
Таким образом, симплекс PQR будет двигаться параллельно исходной плоскости ABC , как бы сопровождая текущую точку P . При этом точки Q и R опишут одинаковые кривые по отношению к кривой P , которые будут находиться от неё на расстоянии соответственно AB и AC . Если угол при вершине A будет прямым, то получим эквидистантные кривые. Также подобным образом можно использовать точечную формулу параллельного переноса для реализации операции копирования геометрических объектов в системах твердотельного моделирования и автоматизированного проектирования.
Определим в симплексе образующую область геометрического тела (рис. 4), ограниченную двумя окружностями.
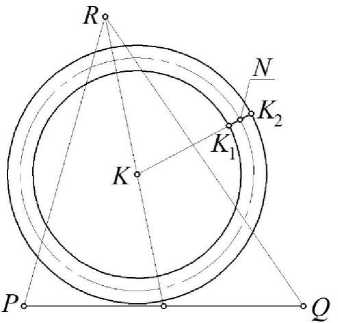
Рис. 4. Геометрическая схема определения образующей области в подвижном симплексе PQR
В качестве примера разместим центр концентрических окружностей K на середине медианы треугольника PQR , проведенной из вершины R :
|
xP + xQ + 2 xR x K = 4 |
|
|
v P + Q + 2 R K =---------- > ^ 4 |
У р + y Q + 2 y R y K = 4 zP + z Q + 2 zR zK" 4 |
Текущую точку N определим с помощью точечного уравнения (1). Представим его в параметрическом виде:
|
r sin ( y- v ) xN = ( xP xK ) . , ' + N V P K) PK sin y / x r sin ( y- v ) , y N = ( У р y K ) |DJ ■ + |PK sin y _ r sin (y- v ) z N = ( zp z K ) | PK | Sin y + |
r sin v xn - xK + xK Q K,\ QK\ sin y r sin v ( yQ - yK ) QK |Sin y+ yK r sin v ( z Q z K ) QK | Sin y+ z K |
Пусть толщина стенки \КХК2 1 = 5 , тогда получим:
NK 1 NK 1
NK NK
N-K- = -^ ^ K = ( K - N + N ,
N - K 2| NK\ 1 v 72| NK\ где INK = J(xN — xK )2 +(yN — Ук )2 + (zN — zK )2 .
С учётом точечного уравнения (2) получим:
|
, , 5 ( 1 - 2 7 ) xM = ( xK xN ) 2|W| + x N |
|
|
M = ( K - N ) 5 ( 1 - 2 7 ) + N ^- 2 NK |
, . 5 ( 1 - 2 7 ) У м =( y K y N ) 2^1 + y N ■ , , 5 ( 1 - 2 7 ) z M =( z K z N ) 2| NK\ + zN |
Таким образом, определив все подвижные точки в симплексе ABCD , получен вычислительный алгоритм моделирования геометрического тела толщиной 5 , визуализация которого представлена на рис. 5.
Инженерная геометрия и компьютерная графика…
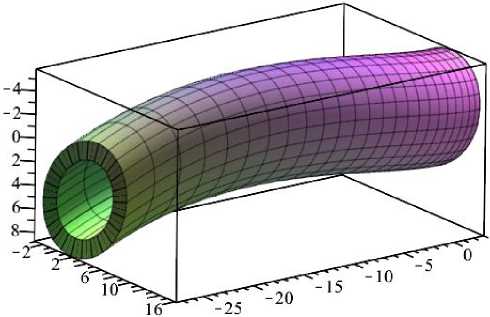
Рис. 5. Визуализация геометрического тела с образующей в виде окружности
Подобным образом можно моделировать каналовые поверхности, если совместить плоскость параллелизма с одной из плоскостей проекций в декартовом симплексе OE 1 E 2 E 3 .
В качестве другого примера представим геометрическое тело с образующей в виде замкнутой кривой типа «синусоида» [25], полученной по аналогии с синусоидой, осью которой является не прямая, а окруж- ность (рис. 6):
N = ( P - K ) p ( v ) + ( Q - K ) q ( v ) + K ^
xN = ( xp - xK) P (v) + (xQ - xK) q (v) + xK • yN = (yp - yK) p (v)+(yQ - yK) q (v)+yK, _ zN =( zp - zK ) P ( v ) + ( zQ - zK ) q ( v ) + zK где p (v) =
sin ( y- v ) ^1 + m 2 + 2 m cos ( mv )
m sin ( у )
; q ( v ) =
| PK | sin ( v )
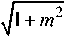
+ 2 m cos ( mv )
| QKm sin ( у )
m – количество волн замкнутой кривой типа «синусоида».
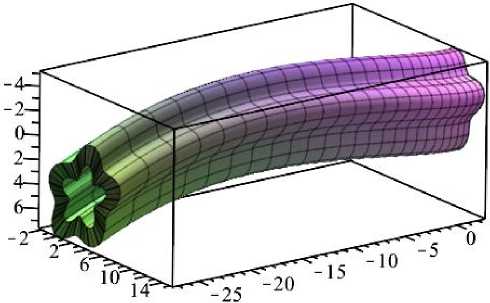
Рис. 6. Визуализация геометрического тела с образующей в виде замкнутой кривой типа «синусоида»
Выводы
Описанный в статье метод подвижного симплекса является не только базовым инструментом кинематической операции твердотельного моделирования, но также может быть эффективно использован для решения широчайшего круга задач геометрического моделирования линий, поверхностей, тел и гиперповерхностей многомерного пространства. Приведенный пример демонстрирует не только реализацию метода подвижного симплекса, но и показывает, как можно использовать точечную формулу параллельного переноса для моделирования поверхностей и тел с плоскостью параллелизма.
Одной из дальнейших перспектив приведенных исследований является определение эквидистантных кривых с помощью точечной формулы параллельного переноса. Важной особенностью является то, что полученные подобным образом эквидистантные кривые могут в дальнейшем использоваться в качестве базовых для построения следующего поколения эквидистантных кривых, в отличие от способа, описанного
Список литературы Кинематическая операция построения геометрических тел в точечном исчислении
- Панчук, К.Л. Математическое и компьютерное моделирование формообразования червячного инструмента / К.Л. Панчук, А.А. Ляшков, В.И. Шарф // Динамика систем, механизмов и машин. - 2016. - № 3. - С. 167-173.
- Рязанов, С.А. Аналитические зависимости кинематического формообразования начальных поверхностей элементов червячной передачи / С.А. Рязанов, М.К. Решетников // Геометрия и графика. - 2019. - Т. 7. - № 2. - С. 65-75. DOI: 10.12737/article_5d2c2dda42fda7.79858292.
- Михайлов, М.И. Моделирование кинематической направляющей внутренней цилиндрической поверхности при обработке концевой фрезой / М.И. Михайлов // Вестник Гомельского государственного технического университета им. П. О. Сухого. - 2018. - № 1(72). - С. 3-10.
- Чекалин, А.А. Кинематическая параболическая поверхность для конструирования архитектурных покрытий / А.А. Чекалин, М.К. Решетников, А.С. Бирзул // Ресурсоэнергоэффективные технологии в строительном комплексе региона. -2018. - № 9. - С. 458-461.
- Гетманцева, В.В. Кинематический способ параметрического описания поверхности фигуры человека / В.В. Гетманцева, Е.Г. Андреева, В.С. Белгородский //EUROASIA SUMMIT Congress on Scientific Researches and Recent Trends - 7, Baku, 06-09 декабря 2020 года. - Baku: FARABI Publishing House, 2020. - С. 577-581.
- Корчагин, Д.С. Способ динамического проектирования кинематической поверхности / Д.С. Корчагин, К.Л. Панчук // Материалы Всероссийской молодежной конференции «Информационно-телекоммуникационные системы и технологии (ИТСиТ-2012)», Кемерово, 20-22 августа 2012 года. - Кемерово: Кузбасский государственный технический университет им. Т.Ф. Горбачева, 2012. - С. 223-224.
- Иванов, Г.С. Нелинейные формы в инженерной графике /Г.С. Иванов, И.М. Дмитриева // Геометрия и графика. - 2017. - Т. 5, № 2. - С. 4-12. DOI: 10.1273 7/article_5953f295744f77.58727642.
- Рачковская, Г.С. Геометрическая модель и компьютерная графика кинематических линейчатых поверхностей на основе триады контактирующих аксоидов «плоскость - круговой конус -круговой конус» / Г.С. Рачковская // Транспорт: наука, образование, производство: сб. науч. трудов Междунар. науч.-практ. конф., Ростов-на-Дону, 18-21 апреля 2017 года. - Ростов н/Д.: Ростовский государственный университет путей сообщения, 2017. - С. 286-289.
- Короткий, В.А. Компьютерное моделирование кинематических поверхностей / В.А. Короткий, Л.И. Хмарова, Е.А. Усманова // Геометрия и графика. - 2015. - Т. 3, № 4. - С. 19-26. DOI: 10.12737/17347.
- Кокарева, Я.А. Синтез кинематических поверхностей на основе эллиптического поворота плоскости / Я.А. Кокарева // Инженерный вестник Дона. - 2018. - № 2(49). - С. 88.
- Гринько, Е.А. Поверхности плоскопараллельного переноса конгруэнтных кривых / Е.А. Гринько // Строительная механика и расчет сооружений. - 2021. - № 3(296). - С. 71-77. DOI: 10.37538/0039-2383.2021.3.71.77.
- Романова, В.А. Образование поверхностей Монжа кинематическим способом в среде AutoCAD / В.А. Романова // Строительная механика инженерных конструкций и сооружений. -2019. - Т. 15, № 2. - С. 106-116. DOI: 10.22363/1815-5235-2019-15-2-106-116.
- Алексюк, А.А. Конструирование кинематических моделей линий и поверхностей в компьютерной графике / А.А. Алексюк // Вестник евразийской науки. - 2019. - Т. 11. - № 6. - С. 87.
- Баглаев, И.И. Кинематический метод моделирования поверхностей в среде FMSLogo /И.И. Баглаев // Вестник Бурятского государственного университета. Математика, информатика. -2016. - № 1. - С. 49-59. DOI: 10.18101/2304-57282016-1-49-59.
- Балюба, И.Г. Точечное исчисление / И.Г. Балюба, Е.В. Конопацкий, А.И. Бумага. - Макеевка: Донбасская национальная академия строительства и архитектуры, 2020. - 244 с.
- Балюба, И.Г. Точечное исчисление. Историческая справка и основополагающие определения / И.Г. Балюба, Е.В. Конопацкий // Физико-техническая информатика (CPT2020): материалы 8-й Международной конференции, Пущино, Московская обл., 09-13 ноября 2020 года. - Нижний Новгород: Автономная некоммерческая организация в области информационных технологий «Научно-исследовательский центр физико-технической информатики», 2020. - С. 321-327. DOI: 10.30987/ conferencearticle_5fd755c0adb1d9.27038265.
- Конопацкий, Е.В. Геометрическое моделирование многофакторных процессов на основе точечного исчисления: специальность 05.01.00 «Инженерная геометрия и компьютерная графика»: дис. ... д-ра техн. наук /Конопацкий Евгений Викторович. - Нижний Новгород, 2020. - 307 с.
- Конопацкий, Е.В. Геометрическая теория многомерной интерполяции / Е.В. Конопацкий // Автоматизация и моделирование в проектировании и управлении. - 2020. - № 1(7). - С. 9-16. DOI: 10.30987/2658-6436-2020-1-9-16.
- Конопацкий, Е.В. Аппроксимация геометрических объектов с помощью дуг кривых, проходящих через наперед заданные точки / Е.В. Коно-пацкий // Информационные технологии. - 2019. -Т. 25, № 1. - С. 46-52. DOI: 10.17587/it.25.46-51.
- Голованов, Н.Н. Геометрическое моделирование /Н.Н. Голованов. -М.: ИНФРА-М, 2019. -400 с.
- Principles of solid modelling in point calculus / E. V. Konopatskiy, A.A. Bezditnyi, M. V. Lagunova, A.V. Naidysh // Journal of Physics: Conference Series: 5, Omsk, 16-17 March 2021. - Omsk, 2021. - P. 012063. DOI: 10.1088/1742-6596/1901/1/012063.
- Konopatskiy, E. V. Solid modeling of geometric objects in point calculus / E.V. Konopatskiy, A.A. Bezditnyi // CEUR Workshop Proceedings: 31, Nizhny Novgorod, 27-30 September 2021. - Nizhny Novgorod, 2021. - P. 666-672. DOI: 10.20948/ graphicon-2021 -3027-666-672.
- Мясоедова, Т.М. Геометрическая модель генерации семейства контурно-параллельных траекторий (эквидистант) обрабатывающего инструмента / Т.М. Мясоедова, К.Л. Панчук // Динамика систем, механизмов и машин. - 2018. -Т. 6, № 2. - С. 262-269. DOI: 10.25206/2310-97932018-6-2-262-269.
- Мясоедова, Т.М. Геометрическое моделирование семейства линий контурно-параллельной обработки карманных поверхностей в изделиях машиностроения / Т.М. Мясоедова, К.Л. Панчук // Динамика систем, механизмов и машин. - 2018. - Т. 6, № 2. - С. 269-276. DOI: 10.25206/2310-9793-2018-62-269-276.
- Конопацький, С.В. Конструювання системи спецгальних плоских кривих типу «синусоХда» методом узагальнених тригонометричних функцт / С.В. Конопацький // Сборник научных трудов SWorld, 2013. - Т. 12. - № 3. - С. 76-80.


