Кинематические характеристики орбитального трехгранника

В практике навигационно-баллистического обеспечения полета космических аппаратов (КА) важную роль играют используемые системы координат. При решении отдельных задач необходимо знание кинематических характеристик для подвижных систем координат, к числу которых относится орбитальная система координат (ОСК) [1 – 4]. При движении КА в окрестности планеты знание кинематических характеристик вращательного движения его ОСК, например, по отношению к планетоцентрической системе координат в ряде случаев также имеет существенное значение. В случае орбитального движения вокруг Земли такой системой координат, как правило, является инерциальная (или абсолютная) геоцентрическая прямоугольная система координат [1] (далее – ИСК). Из задач, решение которых требует знания кинематических характеристик ОСК, отметим следующие: во-первых, это задачи сближения КА на орбите (с целью стыковки, инспекции или перехвата) [4]; во-вторых, задачи расчета кинематических характеристик линии визирования КА – объект исследования (другой КА, какой-либо объект на поверхности планеты, звезда и т.п.) либо в ОСК, либо в связанной с КА системой координат (при наведении подвижных антенных устройств или аппаратуры дистанционного зондирования КА) [5], и, наконец, это задачи, связанные с восстановлением (по измерениям бортовых акслерометров) поля бортовых квазистатических микроускорений [6].

текущих угловых скоростей и ускорений – для ОСК.

1. ОРБИТАЛЬНЫЙ ТРЕХГРАННИК

Как известно [1, 2], для построения ОСК необходимы параметры орбитального движения КА, а именно: r – текущий радиус-вектор центра масс КА в ИСК и v – его абсолютная скорость. В поле ньютонианского тяготения планеты движение центра масс КА описывается следующим векторным дифференциальным уравнением [1, 2]:

d2 r    ц r т = - Г+A w , dt2      r3

где r = | r | - расстояние между центрами масс КА и планеты, ц - гравитационный параметр планеты, а A w - возмущающее ускорение, обусловленное нецентральностью поля тяготения планеты и иными силами негравитационной природы (сопротивление верхних слоев атмосферы планеты, тяга реактивных двигателей системы управления КА, давление солнечного света и т.п. [1]). Поэтому решение уравнения (1) - для заданных начальных условий: r ( t ₀ ) = r ₀ и v ( t ₀ ) = v ₀ , где d r I dt = v , - в виде r = r ( t ) , v = v ( t ) доставляет для всех t >  t ₀ необходимые данные для построения ОСК.

Орбитальную систему координат - O x0y0z0, например, можно ввести следующим образом [2]: ОСК – прямоугольная система с началом в центре масс КА и с осью O x0, направленной по его радиус-вектору r, ось O z0 направляется по вектору кинетического момента в абсолютном движении КА (пропорционального произведению r х v), то есть по нормали к мгновенной плоскости орбиты КА, а ось O y0 дополняет си- стему до правой и, стало быть, лежит в мгновенной плоскости орбиты КА и направлена в сторону его полета (случай r х v = 0 не представляет практического интереса).

Используемые в практике навигационнобаллистического обеспечения полета КА ОСК иногда вводят и иным способом, учитывая те или иные особенности решаемых задач [3, 4]. Отличия обычно состоят только в том, что оси ОСК переименовываются и, быть может, для некоторых из них могут выбираться направления, противоположные указанным выше. Поэтому в общем случае в задаче определения кинематических характеристик ОСК удобно рассматривать движение так называемого орбитального трехгранника, формируемого в пространстве с помощью тройки ортов - e r , e _T и e n , которые задаются следующим образом:

соотношений для расчета компонент вектора

^к оск⁽ t ⁾ .

2. УГЛОВАЯ СКОРОСТЬ ОРБИТАЛЬНОГО ТРЕХГРАННИКА

Как известно [2], при задании в какой-либо подвижной системе координат некоторого постоянного вектора а (например, ортов орбитального трехгранника er, eT или en в ОСК), для того же вектора в неподвижной системе координат (здесь в ИСК) имеет место: a = PиСк a ; и, иск. -1       оск наоборот, а = (P оск) а = P иск а. Поэтому, находя абсолютную производную вектора a , получим [2, 7]

d a   р иск   иск. - 1

dt    P оск⁽ P оск⁾ a .

r r х v e =-; e„ =       ; e^ = e„ х er. (2)

r r n   | r х v | ^T nr

С помощью ортов (2) можно построить матрицу перехода (для векторов) от ОСК к ИСК — P оск и, наоборот, - от ИСК к ОСК, поскольку Р^ = ( P OCK )"¹ = ( Р оСЮ^Т [7]; они имеют (с учетом принятого выше определения ОСК) следующий вид:

иск                                         иск где P оск - производная по t от матрицы P оск .

С другой стороны, по формуле Эйлера [2] эта

d a производная будет равна = to dt

оск

х а и, ста

ло быть, из (5) следует, что имеет место:

e _r

р иск   иск. - 1

■ оск⁽ P оск⁾

р^иск = Г е I е I е 1 • р^оск оск L e r I ^e т I e n J ; иск

e I ; (3)

■ °	-to z	to y ■
® z	°	-to x	, (6)
-to	to	°
y	x

e _n

Кинематические характеристики вращательного движения орбитального трехгранника суть параметры его текущей ориентации в ИСК, задаваемые в виде матриц перехода (3), а также параметры, связанные как с быстротой изменения ориентации этого трехгранника в пространстве: его мгновенной угловой скоростью to _оск ( t ) , так и с быстротой изменения to _оск ( t ) - мгновенным угловым ускорением к _оск ( t ) , которое определяется так [2]:

, . dto, ( t )

к оск( t ) -             •            (4)

Построение матриц (3) задает первую группу кинематических характеристик ОСК (в виде направляющих косинусов). Поэтому далее будут рассматриваться только задачи определения компонент вектора to _оск ( t ) , что не представляет, вообще говоря, практических затруднений, и определения компонент вектора к _оск ( t ) . Следует отметить, что решение последней задачи оказывается нетривиальным, так как требует учета не только кинематических характеристик орбитального движения КА в виде r = r ( t ) , v = v ( t ) , но и структуры действующих на него возмущающих ускорений, поэтому основной целью настоящей статьи является получение

где го x , го y , го z - проекции вектора to _оск на оси ИСК. Соответственно, при проектировании to _оск на соответствующие оси орбитального трехгранника его компоненты будут обозначаться так: го _r , гo_т , го n . Так как согласно (3) иск х-1     оск

("оск) = 'иск, то для определения компонент toоск (в ИСК) достаточно вычислить матрицу P°ск = Г e | e I e "I или, что то же самое, оск r т n абсолютные производные ортов орбитального трехгранника.

r • v

Поскольку v = v_r e r + v _T e _T , где v_r = r = ——

- радиальная скорость, а v _T=| e r х ( v х e r )| -трансверсальная скорость КА, то с учетом (2) получим

■ der   r r -

dt

r ²

r r 1                    v

— = r [ v - er (er • v )]= 7" eT .

Учитывая далее, что c = r х v - вектор кинетического момента орбитального движения КА c и | c | = c = rvT, из (2) получим en = — и, ста-

den ло быть, тогда -"dt- =

•                     ■ cc - cc ---2—, где c

d c

dt r ^х w ,

а dC = С. dC =  . dC, то еСТь отсюда следует dt c dt n dt

d en- = ¹ I f x w — e e • ( r x w ) dt c^{x nL n}               •

Так как w = wr er + wт e т + wnen     и er x w = wтer x eт + wner x en = wтen — wneт, то имеет место:

denrwnwn dt c eт      v т eт •

Наконец, вычислим

ее -ее = т r      г т	( e r _ — ( e r		0 x e т ) z x e т ) y	— ( er x e т ) z 0 ( er x e т ) x	( e r — ( e r	xe ) т / y x e т ) x 0 _	;
	■		0	— ( e тx e n ) z	( e т	xe ) ny
e e — e e = n т       т n		( e т	xe ) nz	0	— ( e т	x e n ) x	•
	—	( e т	xe ) ny	(e xe ) т vnxx		0
Поскольку				отсюда		найдем

deт = d(en x er ) = den x e dt dt dt r

⁺ e n

de x —r~ dt

toОСК - у er х eт + V7 eт х en, постольку век-v т тор угловой скорости ОСК будет определяться так:

vw toОСК _ -7 en + v er •           (8)

^v т

Отсюда, учитывая полученные выше выра-

жения для производных ортов de w       v

——^L = —- e x e +— e x e dt v ^T r _r^{n т}

e _r , e _n , имеем

= Wn e vT n

- —e_r • r^r

Таким образом, получены следующие выражения для производных ортов орбитального трехгранника:

dt r ^{e T} ’

d e _T dt

w

= — e v T

- vT e ■ er ; rr

d e _n dt

wn v т eT •

С учетом (7) матрицу (6) теперь можно записать в явном виде:

Р ИСК ИСК у 1

^ГОСК ⁽ P OCK ⁾

de^ d e^ d e n dt    dt    dt

, T

■ T

^_ ^ ⁽ e т e ^T - e r e ^{T ) +} w n" ⁽ e n e ^T - e т e ^{T )} •

С учетом (5), (6) и формулы Эйлера для некоторого постоянного в ОСК вектора а отсюда непосредственно следует

^to оск ^х a

Г- ⁽ е т e ^{T -} ее _T ^{T )} + w^ ⁽ е _п е _Т ^т

- е тeT)

a •

Учитывая, что е

r

e rx ^ery e_rz

, e т

e т x e т y e т z

e nx

, e n

e ny e _nz

,

e r ^{x e} т

e e ry т z	— e e rz т y		e e т y nz	-e e т z ny
ee rz т x	— e e rx т z	, e тx e n =	ee т z nx	— e e т x nz
e e	— e e			-e,
rx т y	ry т x		т x ny	т y nx

и раскрывая в этом выражении диадные произведения ортов, получим [7]

а его проекции на оси ИСК, соответственно, вычисляются по формулам:

vwvw го = — e +—-e ; го = — e +—-e ; xrnxvrxyrnyvry vw гоz = -7 e-z + 77 erz •(9)

Проектируя вектор to _OCK (8) на оси орбитального трехгранника, также получим

„ОСК _ wn . „ОСК       OCK tor _ —- , Ют _ 0, ton - -7 .

Отметим, что в (8) - (10) wn = en • w, где ur w = - 3- + Aw • Следовательно, wn = en • Aw , r где Aw - вектор возмущающих ускорений в уравнении движения КА (1), то есть на угловую скорость вращения ОСК вокруг радиус-вектора КА r оказывают влияние возмущающие ускорения, возникающие из-за нецентральности поля тяготения планеты, а также ускорения, связанные с наличием сил негравитационной природы, включая тягу реактивных двигателей системы управления КА [1,4],

3. УГЛОВОЕ УСКОРЕНИЕ ОРБИТАЛЬНОГО ТРЕХГРАННИКА

По определению (4) угловое ускорение орбитального трехгранника равно dtoOCK(t)

^{Е оск(} t ⁾        dt •

Поэтому для вычисления Е _ОСК ( t ) продифференцируем выражение для to _ОСК (8), а именно: d to™    d ( v _T) v d e_n   d ( w„ ) w„ d e_r

OCK           L e ^+ L n ^+        n e ^+ n Г dt      dt [ r J  n r  dt    dt [ vT J  r v,  dt "

т                т

Однако, с учетом (7) нетрудно установить, что здесь второй и четвертый члены в правой части сокращаются^ Поэтому далее необходимо вычислить только следующие производные:

[х              •

Vт ] = Vт Г - VтГ . d_ [ wn V wnvT- wnvT r ) r2     ’ dt I V J vT2'

LT

OCK OCK „

Поскольку здесь E _OCK = £ _n e n + £ _r e r и £ O ^CK = 0 , то с учетом приведенных выражений для производных получим

Таким образом, получены все кинематические характеристики ОСК. Соотношения для компонент угловых ускорений ОСК (14) харак-

теризуются влиянием на их значения перечислявшихся выше возмущающих сил. Особенно-

OCK

^£ r

wv - wv n т n т

v

2 т

OCK

^£ n

vTr - vr т т

r ²

Отсюда видно, что для вычисления тождественно ненулевых компонент E _OCK (11) также необходимо указать выражения и для •                        ■

стью соотношений (14) является то, что помимо влияния возмущающих ускорений, обусловленного компонентами wT = eт • Aw и wn = en • Aw , OCK на величину £ r также влияет компонента dw d„ = e„ • q = e„ • -г, что связано со скоростью nn ndt

производных v _т и w_n .В связи с этим вначале найдем производные v_r , v _т , вычисляя

изменения ускорения начала орбитального трехгранника, помещаемого в центр масс КА. Учет влияния q_n может быть существенным при решении задач о сближении КА [4].

w =

d v = ^{d (} v r e r ^{+ V} T e T ) dt dt

учетом (7) получим

■         der    ■         de T w = vr er + vr dt + vt et+ vt dt =

4. ВСПОМОГАТЕЛЬНЫЕ СООТНОШЕНИЯ ДЛЯ РАСЧЕТА КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК ОРБИТАЛЬНОГО ТРЕХГРАННИКА

. •     . vvV

= v r e r + v T e T ⁺     e T ⁺ w n e n — у e r .

Сгруппировав здесь соответствующим образом

2 vvv члены, определим wr = vr--, wT = vт +, то есть отсюда следует vvv vr = wr + "у; VT= wT—rrr •

Далее, чтобы найти выражение для вычисления w_n , продифференцируем w = w r e _r + w _T e _T + w_n e _n , а именно:

d w

-г- = q = w, e, + wT eT + w„ e„ + dt 4 r r T T n n de     dede

+ w, -+ + W_T    + w„ —T" .

^r dt ^T dt ⁿ dt

Умножая скалярно полученное выражение на ww en с учетом (7), получим qn = en • q = wn + V n , то есть отсюда получим искомое выражение для wn:

ww wn = Qn--Tn .          (13)

Итак, подставив (12), (13) в (11), получим следующие выражения для проекций вектора E _OCK :

оск 1 (     2 w_Tw_n v_rw_n )

s_r =    q„ - — + r²^" ;

r       v _т V          v _т         r J

pOCK        OCK

^£ т ⁰ ; ^£ n

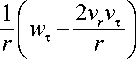
При вычислении компонент углового ускорения орбитального трехгранника EOCK (14), как это было отмечено выше, необходимо знание производной вектора абсолютного ускорения dw

—дГ = q (в ИСК). Очевидно, что ее можно опре- делить, если задать ускорение центра масс КА, исходя из уравнений его орбитального движения (1).

Итак, перепишем уравнение (1) в виде

Ц w = —у er +A w, r2

где A w - возмущающее ускорение, задаваемое в соответствии с принятой математической моделью орбитального движения КА. Поскольку в общем случае в составе A w возможно наличие управляющих ускорений, постольку далее примем

A w = A g ( r , v ) + p ( t ) , (15) где p ( t ) - вектор управляющих ускорений, а A g ( r , v ) - вектор остальных возмущающих ускорений, учитываемых в модели орбитального движения КА. Выбор последней зависит от класса орбиты КА и требуемой точности моделирования движения его центра масс [1]. Следует отметить, что в общем случае A g ( r , v ) может зависеть и от текущей ориентации КА и, стало быть, от текущего времени t при задании некоторой программы углового движения КА. Последнее при исключении из рассмотрения аэродинамических сил (например, в силу их малости на высоких орбитах), как правило, не будет иметь заметного влияния на решение рассматриваемых здесь задач. Поэтому с учетом (15) абсолютное ускорение центра масс КА далее запишем в следующем виде:

w = —т e r + A g ( r , v ) + p ( t ) ,      ⁽¹⁶⁾

r

и, дифференцируя затем (16), получим

q =

d w dt

e_T r - 2 e_T r

-^ r 3 r

+

SA g ( r , v ) SA g ( r , v )

d r

d v

w + d p t! . (17) dt

SA g ( r, v )        dA g ( r , v )

Строки матриц G, = ——-, G„ = — „ r       8 r        v суть соответствующие градиенты компонент вектора Ag(r, v). Поскольку в (17) —— err ^err = 4 (vTeT - 2vrer ) = 4 (v - 3vrer ) , rrr то первое слагаемое в правой части (17) – вектор, ортогональный орту en . Следовательно, qn = en ‘ q в (14) определяется следующим выражением:

Q n = e n G r v ⁺ e n G v w ⁺ e n P ⁽ t ) ,      ⁽¹⁸⁾

Сложность вычисления матриц G _r и G _v в (16) непосредственно связана со сложностью принятой модели орбитального движения КА и при численном моделировании параметров движения его центра масс наиболее рациональным подходом к вычислению q_n согласно (18) является вычисление матриц G _r ( r , v ) и G v ( r , v ) в процессе численного интегрирования уравнений движения КА (1). То же самое относится и к вычислению производной p ( t ) . При этом элементы матриц G_r ( r , v ) и G v ( r , v ) можно определять только на начало каждого шага интегрирования уравнений движения КА как соответствующие вариации компонент вектора A g ( r , v ) для специально задаваемых приращений r и v .

ЗАКЛЮЧЕНИЕ

В настоящей статье приведены соотношения для расчета кинематических характеристик моделирующего орбитальную систему

координат орбитального трехгранника, к которым относятся компоненты векторов угловых скоростей и ускорений. Если при этом начало ОСК совмещается с центром масс КА, на который действуют силы, обусловленные как нецентральностью поля тяготения планеты, так и иными силами негравитационной природы, включая управляющие, то расчет кинематических характеристик ОСК имеет определенные особенности, связанные с необходимостью явного учета производных от абсолютного ускорения центра масс КА в силу принятой для него математической модели орбитального движения.