Кинематические свойства электротехнических комплексов с системой слежения за солнцем, полученные методом полиномиальной аппроксимации небесных координат

Автор: Сологубов Андрей Юрьевич, Кирпичникова Ирина Михайловна

Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power

Рубрика: Альтернативные источники энергии

Статья в выпуске: 3 т.19, 2019 года.

Бесплатный доступ

Синтез и исследование любых гелиоустановок сопряжён с необходимостью выявления регулярных особенностей движения рабочего органа, угловое положение которого регулируется в эвклидовом пространстве. Эту информацию можно получать обработкой данных об угловом положении Солнца в заданных географических координатах. Локальность во времени всех алгоритмов вычисления солнечной позиции не позволяет анализировать годовой и суточный цикл движения Солнца в едином виде. Для решения этой задачи мы применили новый принцип обработки результатов расчёта, который заключается в следующей последовательности действий. Используя астрономический алгоритм NREL SPA, в основе которого лежат нелинейные тригонометрические уравнения, построены двухмерные поверхности азимутальных из зенитных углов. Путём аппроксимации этих поверхностей полиномами высокого порядка и дифференцирования этих полиномов по времени получены поверхности азимутальных из зенитных угловых скоростей, ускорений и рывков. Расчётные коэффициенты полиномов сведены в таблицы, чтобы в дальнейшем их можно было применять для оценочных расчётов в рамках структурного и параметрического синтеза электротехнических комплексов слежения за Солнцем в заданном географическом местоположении. Для проверки степени совпадения с готовыми локально-временными онлайн-алгоритмами мы выбрали онлайн-калькулятор MIDC SPA Calculator. Сопоставление результатов полиномиальной аппроксимации с данными расчётов по этому онлайн-калькулятору показывает хорошее совпадение результатов и низкий уровень ошибок.

Еще

Двухмерная поверхность, угол азимута, угол зенита, скорость зенита, скорость азимута, ускорение азимута, ускорение зенита, рывок азимута, рывок зенита, полиномы высокого порядка

Короткий адрес: https://sciup.org/147232746

IDR: 147232746 | DOI: 10.14529/power190308

Текст научной статьи Кинематические свойства электротехнических комплексов с системой слежения за солнцем, полученные методом полиномиальной аппроксимации небесных координат

Электротехнические комплексы для слежения за Солнцем – это такие системы, в которых сигнал ошибки формируется оптико-электронным прибором, реагирующим на отклонение своей оптической оси от направления на небесные источники излучения (в нашем случае в качестве такого источника используется Солнце).

Эти комплексы обладают рядом особенностей, которые позволяют выделить их в отдельный класс астроследящих систем.

Решение весьма актуальных задач кинематического [1] и динамического анализа систем слежения за Солнцем (в рамках их структурного и параметрического синтеза) требует использования достаточно точного расчёта параметров суточного и годового углового движения Солнца на небосводе, на основе которых формируются характеристики угловых скоростей, ускорений и рывков (далее «кинематические кривые»).

Известен достаточно прочно устоявшийся набор алгоритмических инструментов [2]. Впервые опубликованный Миусом в [3] алгоритм был переработан Редой и Андреасом, а затем представлен в пошаговой форме в известном алгоритме NREL SPA [4], который широко используется в задачах расчёта энергоэффективности. В качестве примера можно привести системы управления SPPA-T3000 [5]. Погрешность расчёта зенитных и азимутальных углов Солнца в этом алгоритме составляет ±0,0003° (в период 2000 до н. э. – 6000 года н. э.).

В наших предыдущих работах [6, 7] мы сообщали об использовании в своих исследованиях другого алгоритма под названием SPC, разработанного Национальным управлением океанических и атмосферных исследований (NOAA), по причине удовлетворительной для наших задач точности и отсутствия высоких требований к вычислительным мощностям. Онлайн-калькулятор NOAA Solar Calculator [8] работает именно на его основе.

Полученный со временем опыт его использования показал, что расчёт по аналитическим формулам в том виде, в котором они представлены, приводит к некорректному отображению углов азимута и зенита для высоких широт (расположенных от 60° магнитной широты и выше). Это один из двух факторов, который заставил отложить применение SPC для других целей. Вторым фактором явилось желание продемонстрировать то, что кажущаяся сложность NREL SPA – фактор в достаточной степени субъективный, нивелируемый мощностями современных вычислительных устройств.

Тем не менее существенная нелинейность тригонометрических уравнений в большинстве методов расчёта [3, 9–14] позволяет получить только кривые азимутальных и зенитных угловых положений. Для разработки и кинематического анализа электроприводов требуются тахограммы, а для динамических исследований необходимы также кривые угловых ускорений и в некоторых случаях рывков [15].

Впервые обработка данных суточного изменения азимутальных и зенитных углов Солнца была продемонстрирована в монографии Принсло и Добсона [16]. Взятые из [17] результаты расчёта они продифференцировали по методу Эйлера и получили тахограммы 1-координатного электропривода систем слежения за Солнцем, которые могут использоваться для проектирования следящего привода и его исследования. Было определено, что Солнце движется в среднем с угловой скоростью около 0,25 °/мин. Они предложили способ функционирования системы слежения за Солнцем в таком режиме, а именно уменьшить скорость двигателя примерно до 20 об/мин и использовать передачу «винт – гайка» с передаточным отношением 1:15 000. Тогда скорость вращения составит около 0,00133 об/мин. Такая комбинация будет способна поддерживать требуемые скоростные режимы. Для Челябинской области подобные данные и расчёты отсутствуют.

Говоря об особенностях локально-временных высокоточных алгоритмов расчёта, высокая степень нелинейности тригонометрических уравнений, которые используют Принсло и Добсон, осложняет процессы разработки математических моделей, а также получение экспериментальных данных. Здесь пригодился бы такой математический подход, который позволит убедительно определить кинематические кривые или даже дать прогноз на длительных интервалах времени путём обработки результатов расчёта и анализа.

Для этого мы использовали полиномиальную аппроксимацию высокого порядка [18]. Сначала мы получили аппроксимацию на двухвременном интервале (сутки и год) и провели анализ неравномерности углового движения Солнца. На основе полученных поверхностей мы определили полиномиальные коэффициенты для расчёта кривых угловых скоростей, ускорений и рывков, а также определили их минимальные и максимальные значения по месяцам (январь – декабрь).

Формирование временных баз данных для обработки алгоритмом

В основе работы алгоритма NREL SPA лежит пошаговое численное решение ряда астрономических уравнений, описывающих движение Солнца относительно выбранного географического местоположения в сферической системе координат. Кроме прочего, он учитывает влияние отражающей способности атмосферы Земли и связанное с ним изменение угла подъёма Солнца [4]. Для расчёта кинематических кривых необходимо рассчитать суточный и годовой ход углов положения θAz и θZen, т. е. в предельном случае необходимо охватить весь временной промежуток.

Практический интерес представляет движение Солнца за 1 цикл слежения в сутки, т. е. за промежуток времени между восходом и заходом. В нашем случае был выбран интервал времени 01:00–21:00 с шагом 10 мин (600 с), что перекрывает как осенне-зимние, так и весенне-летние периоды. Следует отметить, что с учётом суточного tсуток и годичного nгода изменения функция расчёта углов становится двухпараметрической.

Мы разработали новый принцип обработки результатов расчёта, чтобы решить такую задачу. Расчёт параметров движения Солнца осуществляется путём синтеза временных баз данных, где столбцами является время суток δ (матрица «Время суток»), а строками – номер месяца M (матрица «Номер Месяца»), день года D и т. д., охватывая целиком и полностью время всего 2019 года. Для генерации данного массива была использована специальная процедура, суть которой заключается в следующем: при решении задачи временные параметры задаются в виде векторов, которые затем преобразуются в указанные «матрицы времени», например, доля времени суток δ, номер месяца в году M, номер дня в месяце MN и номер дня в году N, т. е.:

N = n

T дня

года

- 1_день • * ^п (365/366)_день J ^

1 365

1 1 - 365

П ш_вр_с 1 - 365

MN = п Тня

месяца [_^п 1_января • * ^п 31_декабря

Ч 1 ... 365

1 1 31

П ш_вр_с 1 - 31

" \ 1 - 365 "

_т __г " т 1 1 - 12

M = ^П месяца_года = _ ^П номер_января •” ^П номер_ декабря ] ^ : ; : : ;

_ ^П ш_вр_с ¹ - ¹² _

5 = 5 д я суток = [З начало - 5^ ] T = [ 01:00 ^ 22: 00 ] ^т ^

\ 1 - 365 "

1 01:00 - 01:00

: : : : ,

П ш вр с 22:00 - 22:00

где n _{ш вр с} – при шаге Δt_суток = 10 мин составляет 138 «шагов по времени».

В табл. 1 показан принцип совместного функ- бая выбранная дата, например, 8 декабря 2019 года)

ционирования временных баз данных. Полученный путём введения процедуры «Выбор значения из

массив может использоваться для выбора конкретно- массива» . На рис. 1 показано графическое отобра-

го времени в конкретный день года (допустима лю- жение сформированных временных векторов.

Таблица 1

Схема формирования временно́й матрицы

Год

Сезон

Зима

Весна

Лето

Осень

Зима

Месяц

Январь

Февраль

Март

Май

Июнь

Август

Сентябрь

Ноябрь

Декабрь

День года

151

152

243

244

334

365

1:00:00

6:45:00

12:30:00

18:15:00

22:00:00

Рис. 1. Изменение номера дня в году (а), а также номера месяца и номера дня в месяце (б)

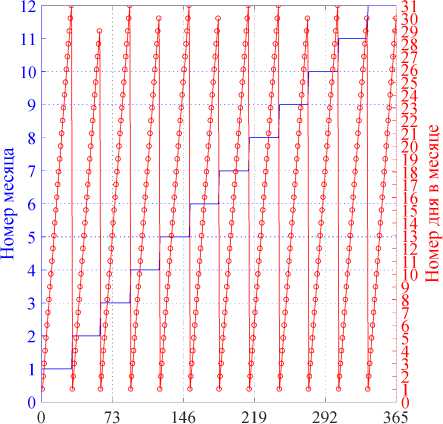
День года (б)

Выбор общего шага по времени для времени суток 10 мин (Δt_суток = 600 с), а шаг по времени для номера дня года 1 день (Δt года = 1 день) продиктован удобством формирования конфигурации вычислительной сетки: количеством часов в сутках и большой годовой временной протяжённостью. Приводить все расчётные формулы из алгоритма, на наш взгляд, не требуется, так как все они присутствуют в цитируемом техническом отчёте [4]. Нужно лишь переработать алгоритм для обработки синтезированных многомерных временных массивов, что и было проделано авторами.

Ниже описываются исходные параметры, которые необходимы для определения положе- ния Солнца. Представленный в табл. 2 набор исходных параметров входит в состав уравнений, используемых при вычислении солнечного вектора [4].

По данным Челябинской центральной гидрометеорологической службы (ЦГМС) [19] и климатической базы данных [20], в табл. 2 дополнительно включены значения атмосферного давления и средней температуры для Челябинска. На рис. 2 и 3 представлено их графическое изображение. Среднее атмосферное давление обычно даётся в миллиметрах ртутного столба (мм. рт. ст.). Для перевода в миллибары (мбар) нужно умножить атмосферное давление на коэффициент 4/3.

Таблица 2

Исходные данные для расчёта параметров суточного движения Солнца в Челябинске

Наименование	Обозначение и единицы измерения	Значение
Город	—	Челябинск
Год	Y	2019
Широта	φ, ° ′ ″	55°09′14″ (55,1540200°)
Долгота	ζ, ° ′ ″	61°25′44″ (61,4291500°)
Часовой пояс	TimeZone, ч	+5
Высота над уровнем моря	H, м	219
Атмосферное давление	P, мбар	978…993
Средняя температура	T, К	257…292

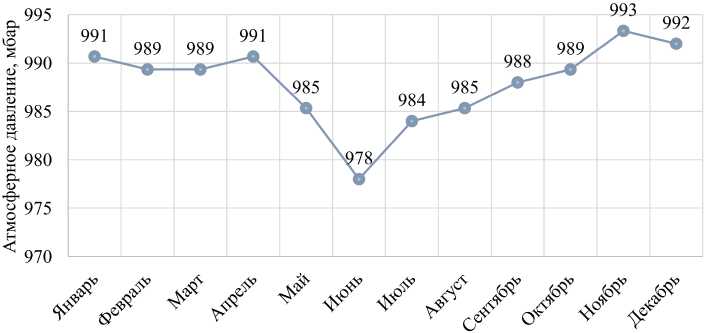
Рис. 2. Атмосферное давление в Челябинске по месяцам

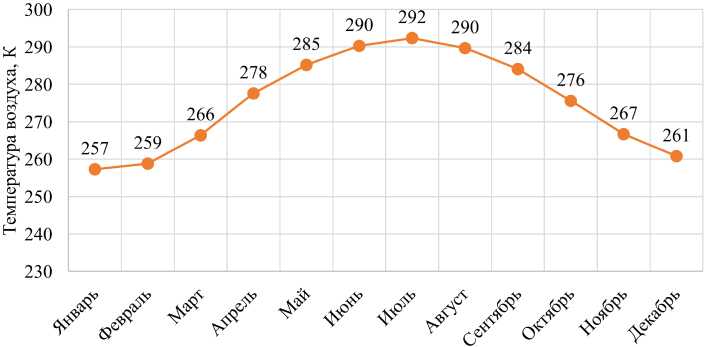
Рис. 3. Средняя температура в Челябинске по месяцам

а)

б)

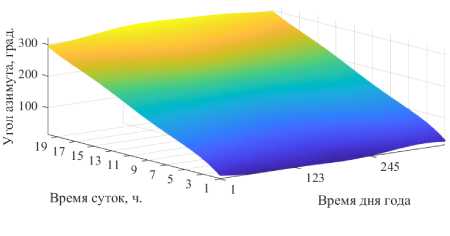
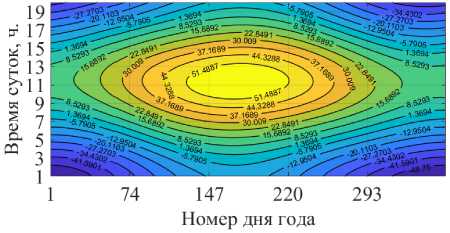
Рис. 4. Поверхности углов зенита (а)

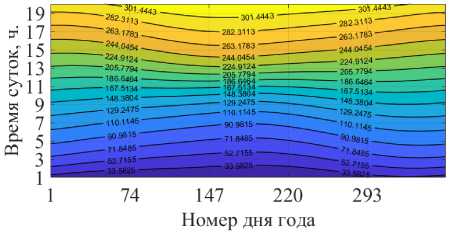
и азимута (б) в 2019 году в Челябинске

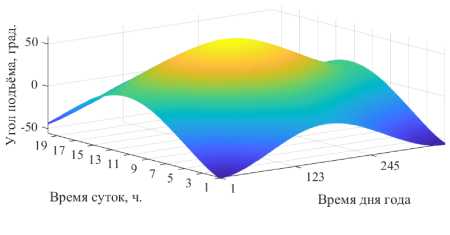
На рис. 4 приводятся наглядные результаты расчётов поверхностей углов зенита и азимута за 2019 год.

Дифференцирование углов азимута и зенита по времени с помощью полиномиальной аппроксимации высокого порядка

Графики азимутальных и зенитных углов (θAz и θZen) на рис. 4 теперь могут использоваться для определения кинематических кривых. В классиче- ском случае (двухкоординатный опорно-поворотный механизм) скорости определяются путём простого дифференцирования углов азимута и зенита (θAz и θZen) по выбранному временному параметру tсуток и nгода (наклон в каждой точке равен скорости слежения за Солнцем (град/10 мин). На рис. 5 показано, как это можно осуществить.

На первый взгляд, решение этой задачи не должно составлять труда, поэтому уравнения можно было бы просто продифференцировать по

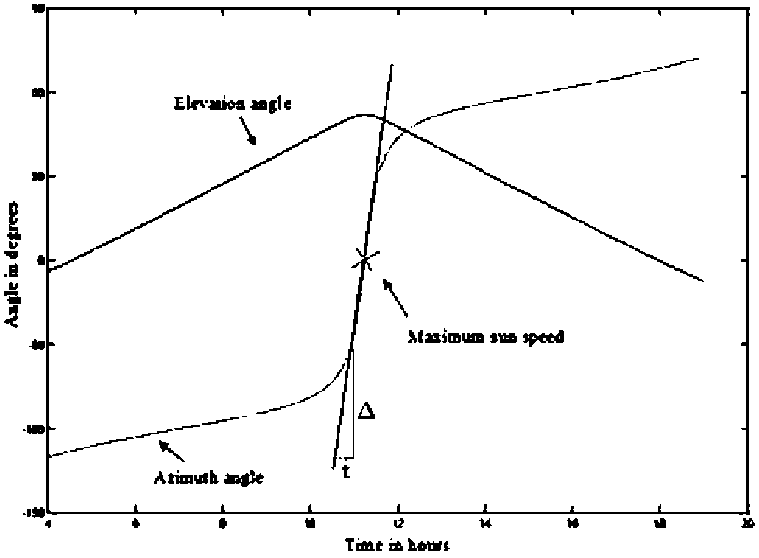
Рис. 5. Определение угловой скорости слежения по кривым углов азимута и зенита [16]

времени, тем более что их структура выглядит так, словно для этого очень хорошо подходит (содержит ярко выраженные временные параметры).

Однако попытка получить таким путём аналитические зависимости для угловых скоростей по азимуту и по зениту, как уже упоминалось ранее, оказывается чрезвычайно громоздким и неудобным для дальнейших вычислений процессом.

В связи с тем, что расчёты сосредоточены в программной среде MATLAB, наилучшим для получения угловой скорости вариантом является осуществить полиномиальную аппроксимацию высокого порядка [18], а затем продифференцировать полученный полином по времени.

Для построения аппроксимирующего полинома заданной степени, приближающего функцию одной переменной, заданную соответствующими массивами значений, в системе MATLAB может использоваться функция polyfit, реализующая метод наименьших квадратов. Имеем q = polyfit(x, y, n), где y – вектор значений функции, в нашем случае это время суток от 01:00 до 20:59:59 ч; x – вектор значений аргумента; n – степень аппроксимирующего полинома.

Пусть имеется массив значений время суток от 01:00 до 20:59:59 ч (столбец для выбранного дня года из массива времени) и массив соответствующих им значений углов азимута и зенита (столбец для выбранной даты из массива углов). Вся процедура осуществляется в соответствии со следующим «псевдокодом»:

Алгоритм : полиномиальная аппроксимация высокого порядка для получения кинематических кривых по результатам расчёта углового положения Солнца в выбранном географическом местоположении 1. «Степень полинома» = n;

2. Цикл для i = 1 до «Число дней в году»
3. x(:,i) = «Доля времени суток»;
4. y(:,i) = «Угол Азимута (Зенита)»;
5. θ_p = polyfit(x(:,i), y(:,i), «Степень полинома»);
6. ω_p = polyder(p); «Полиномиальные коэффициенты для угловых скоростей»
7. a_p = polyder(ω_p); «Полиномиальные коэффициенты для ускорений»
8. j_p = polyder(a_p); «Полиномиальные коэффициенты для рывков»
9. θ_f(:,i) = polyval(θ_p,x(:,i)); «Полином для углов»
10. ω_f = polyval(ω_p,x(:,i)); «Полином для скоростей»
11. a_f = polyval(a_p,x(:,i)); «Полином для ускорений»
12. j_f = polyval(j_p,x(:,i)); «Полином для рывков»
13. Конец

В результате получим матрицу коэффициентов полиномиальной аппроксимации высокого порядка θ p , ω p , a p и j p .

Заметим, что поиск оптимальной по методу наименьших квадратов функции не всегда позволяет получить хороший результат. Более того, при увеличении степени полинома качество приближения может ухудшаться [18]. Эмпирическим пу- тём и другими экспериментами с кодом было установлено, что наилучшее качество аппроксимации даёт полином 6-й степени.

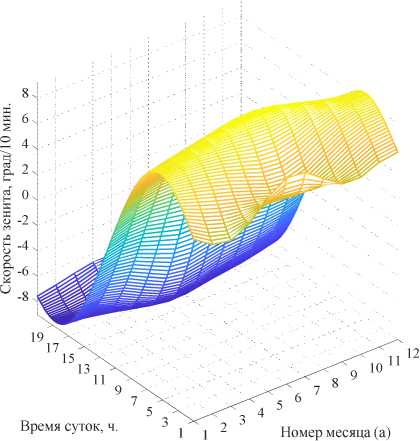
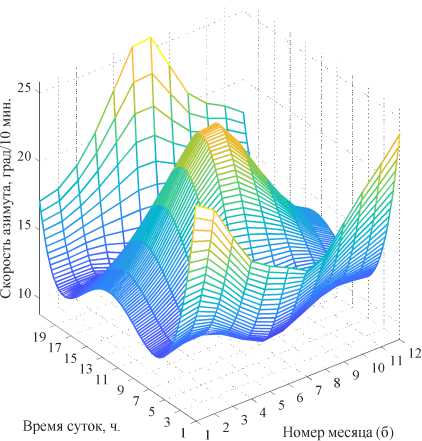
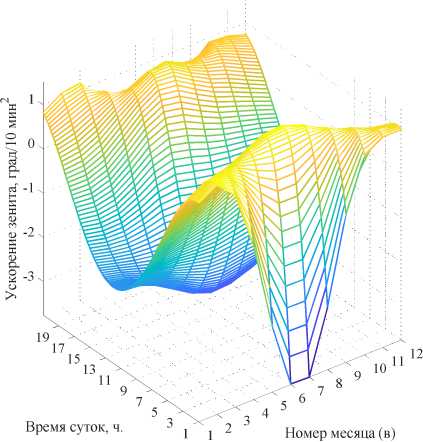
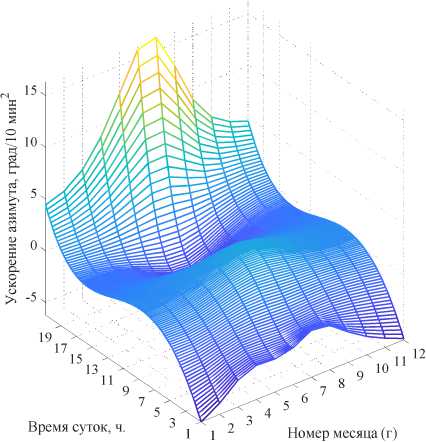
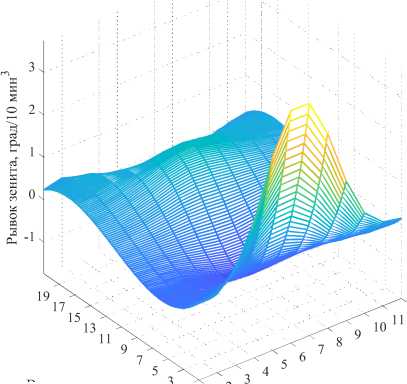
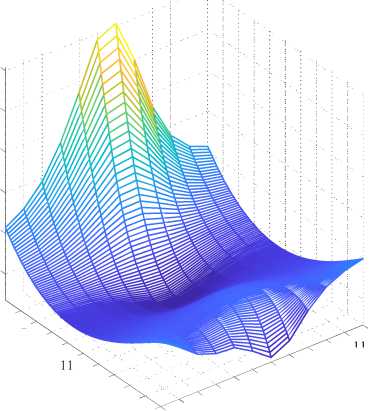
На рис. 6 показаны рассчитанные путём полиномиальной аппроксимации высокого порядка и дифференцированием по времени двухмерные поверхности (тахограммы) угловых скоростей (рис. 6а, б), ускорений (рис. 6в, г) и рывков (рис. 6д, е) по углам зенита и азимута.

На рис. 7а, б приведены кривые, на которых отображены углы зенита и азимута, рассчитанные в MATLAB, по онлайн-калькулятору MIDC SPA Calculator и по коэффициентам полиномиальных уравнений. Графики соответствуют дате «1 января 2019 года».

Несоответствие между углами зенита и азимута, рассчитанными по онлайн-калькулятору MIDC SPA Calculator и в MATLAB, а также между углом зенита, рассчитанным по онлайн-калькуля-тору MIDC SPA Calculator и по коэффициентам полиномиальных уравнений, показаны на рис. 7в, г. Наибольшее отклонение от значений, полученных в калькуляторе MIDC SPA Calculator, наблюдается c 7:30:00 до 10:30:00 по местному времени и квадрат ошибки составляет ≈ 0,3 град2. Судя по тому, что квадрат ошибки нигде не превышает 1, погрешность расчёта не превышает 1 градус. Следовательно, при наличии подобной неравномерности, в отсутствие резких, непрогнозируемых возмущений достигаемая расчётная точность составит порядка 1 градуса для Челябинска при полиномиальной аппроксимации высокого порядка.

Для демонстрации отдельных кинематических кривых мы выбрали дату 1 января 2019 года в Челябинске и выбрали соответствующие указанной дате характеристики, которые представлены на рис. 8).

Кратко проанализируем формы полученных кинематических профилей. Во-первых, форма тахограммы в процессе углового хода по углу зенита помимо вполне ожидаемого «осесимметричного характера» имеет характерное нулевое значение в 12:00, когда угол зенита достигает максимума. Во-вторых, несмотря на ярко выраженные максимумы скоростей в 5:00 и в 19:00, имеющие значение по модулю 8,9823/10 мин, они лежат за пределами восхода и заката Солнца в январе. Это означает, что в качестве максимальных скоростей следует принимать скорости, лежащие в пределах видимого углового движения январского Солнца. В свою очередь, профиль ускорения на этом временном интервале представляет собой параболу, смещённую по оси ординат в отрицательную область. Максимальное по модулю значение ускорения составляет 2,5 град/10 мин2. Что касается профиля рывка, то он имеет форму сглаженной сигмоиды, нулевое значение которой совпадает с таковым в полдень (12:00), а максимальное по модулю значение составляет ≈ 1 град/10 мин3.

Время суток, ч.

Номер месяца (д)

о ci

Время суток, ч.

Номер месяца (е)

9 10

Рис. 6. Двухмерные поверхности (тахограммы) угловых скоростей (а, б), ускорений (в, г) и рывков (д, е) по углам зенита и азимута

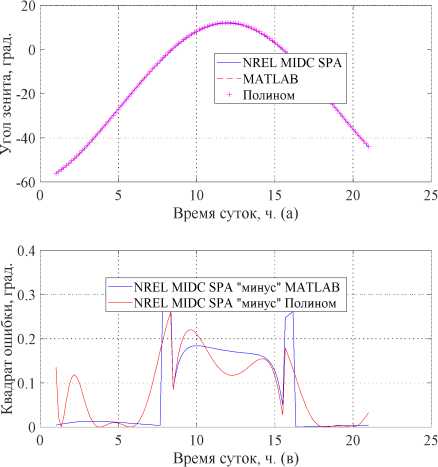
Рис. 7. Угол подъёма 1 января 2019 года в Челябинске и квадраты ошибок между углами зенита и азимута, рассчитанными по онлайн-калькулятору MIDC SPA Calculator и в MATLAB, а также между углом зенита, рассчитанным по онлайн-калькулятору MIDC SPA Calculator и по коэффициентам полиномиальных уравнений

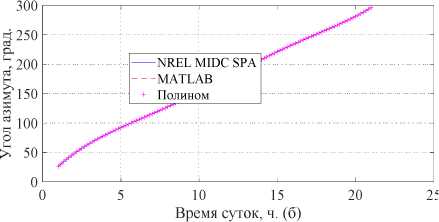
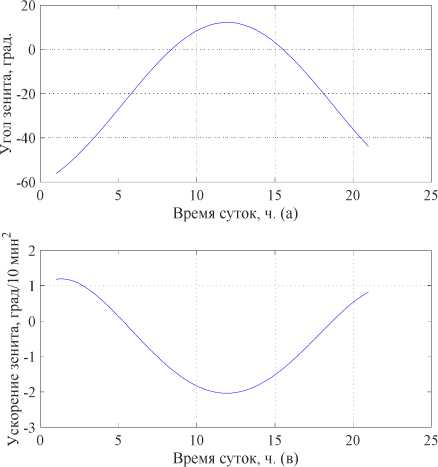
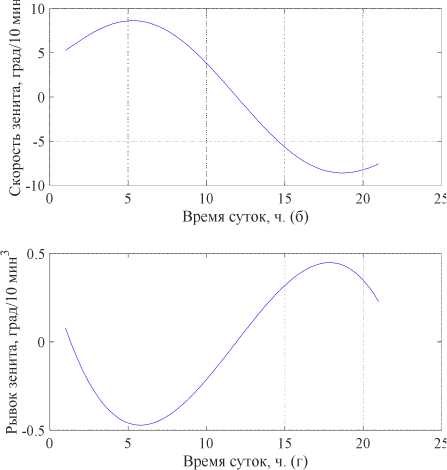
Рис. 8. Кинематические кривые для 1 января 2019 года в Челябинске

На текущем этапе исследований можно считать достаточно убедительным качество полиномиальной аппроксимации на длительном интервале времени и принять для дальнейших исследований степень полинома 6. При определении этих коэффициентов следует иметь в виду, что структурные свойства модели должны быть корректно отражены.

Об изменении астрономических констант

Известно, что астрономические константы со временем могут изменяться. С момента выпуска публикации [4] прошло 11 лет, однако точность расчётов не пострадала. Вполне вероятно, что NREL периодически поддерживает и корректирует астрономические константы, однако эта информация не опубликована.

Результаты расчётов

На основе данных измерений методом полиномиальной аппроксимации высокого порядка определены коэффициенты полиномов, построены траектории и даны прогнозы максимальных значений кинематических параметров в Челябинске на 2019 год. Результаты этих расчетов сведены в табл. 3.

Таблица 3

Характерные значения кинематических параметров системы слежения за Солнцем в Челябинске,

1 января 2019 года (на интервале видимого движения Солнца от рассвета до заката)

	Угол	Скорость	Ускорение	Рывок
Max	12,5°	7°/10 мин	2,5°/10 мин²	1°/10 мин³

Таблица 4

Полиномиальные коэффициенты, описывающие кинематические характеристики систем слежения за Солнцем в Челябинске за январь – июль – декабрь 2019 года для зенита

G II ^ co д д ц к 3 д о Д Д о	Угол			Угловая скорость
	Январь	Июль	Декабрь	Январь	Июль	Декабрь
	–8,76E-06	–4,69E-05	–9,75E-06	–5,25E-05	–0,00028	–5,85E-05
	0,000621	0,00332	0,00068	0,003105	0,016601	0,003399
	–0,01358	–0,08511	–0,01485	–0,0543	–0,34042	–0,05941
	0,061718	0,929099	0,076235	0,185155	2,787296	0,228706
	0,482157	–4,18831	0,354436	0,964313	–8,37661	0,708872
	4,183276	12,94293	4,835616	4,183276	12,94293	4,835616
	–60,9369	–22,2476	–60,6282	–	–	–
	Угловое ускорение			Рывок
	Январь	Июль	Декабрь	Январь	Июль	Декабрь
	–0,00026	–0,00141	–0,00029	–0,00105	–0,00562	–0,00117
	0,01242	0,066404	0,013596	0,03726	0,199212	0,040788
	–0,16291	–1,02126	–0,17824	–0,32581	–2,04253	–0,35648
	0,37031	5,574593	0,457413	0,37031	5,574593	0,457413
	0,964313	–8,37661	0,708872	–	–	–

Таблица 5

Полиномиальные коэффициенты, описывающие кинематические характеристики систем слежения за Солнцем в Челябинске за январь – июль – декабрь 2019 года для азимута

G II ^ со д 3 д	Угол			Угловая скорость
	Январь	Июль	Декабрь	Январь	Июль	Декабрь
	0,0000070	0,0000739	0,0000057	0,0000420	0,0004435	0,0000343
	–0,0000703	–0,0039645	0,0000189	–0,0003514	–0,0198226	0,0000943
	–0,0115633	0,0703331	–0,0136694	–0,0462531	0,2813326	–0,0546776
	0,3662034	–0,4196496	0,3831699	1,0986103	–1,2589488	1,1495098
	–4,1394326	0,0486388	–4,1047103	–8,2788653	0,0972776	–8,2094207
	31,8268482	17,4458077	30,8703441	31,8268482	17,4458077	30,8703441
	–1,6796336	–4,0347689	3,1748163	–	–	–
	Угловое ускорение			Рывок
	Январь	Июль	Декабрь	Январь	Июль	Декабрь
	0,0002098	0,0022176	0,0001717	0,0008393	0,0088703	0,0006869
	–0,0014057	–0,0792904	0,0003772	–0,0042170	–0,2378711	0,0011315
	–0,1387592	0,8439977	–0,1640329	–0,2775184	1,6879955	–0,3280658
	2,1972206	–2,5178976	2,2990196	2,1972206	–2,5178976	2,2990196
	–8,2788653	0,0972776	–8,2094207	–	–	–

Рассчитанная угловая скорость по порядку величины соответствует рассчитанной в схожих условиях [16], но с поправкой на географическое местоположение, и составляет 7°/10 мин против 2,5°/10 мин.

Заключение

Дальнейшие исследования не только максимальных, но и минимальных значений параметров, позволят установить требуемый диапазон скоростей для нормальных условий функционирования, что будет использоваться для дальнейшего струк- турного и параметрического синтеза рассматриваемых систем слежения за Солнцем. Полученные результаты могут представлять как естественнонаучный интерес, так и найти применение в других прикладных задачах геофизики и навигации [21].

При необходимости статистической обработки результатов расчёта для убедительного прогноза кинематических параметров на длительных интервалах времени следует учитывать взаимосвязанность процессов по суткам и по годам.

Примеры полиномиальных коэффициентов для кинематических кривых сведены в табл. 4, 5. Данные коэффициенты относятся к январю, июлю и декабрю.

Список литературы Кинематические свойства электротехнических комплексов с системой слежения за солнцем, полученные методом полиномиальной аппроксимации небесных координат

Нго Сян Кыонг. Анализ конструктивных схем электромеханических систем солнечных батарей / Нго Сян Кыонг // Известия ТулГУ. Технические науки. - 2013. - Т. 1. - P. 322-325.
Demenkova, T.A. Modelling of algorithms for solar panels control systems / T.A. Demenkova, O.A. Korzhova, A.A. Phinenko // Procedia Computer Science. - 2017. - Vol. 103 - P. 589-596. DOI: 10.1016/j.procs.2017.01.072
Meeus, J. Astronomical Algorithms / J. Meeus. - Willmann-Bell Inc., 1991. - 477 p.
Reda, I. Solar Position Algorithm for Solar Radiation Applications (Revised) / I. Reda, A. Andreas // NREL/TP-560-34302. Golden (Colorado). - January 2008. - 56 p. DOI: 10.2172/15003974
Энергия солнца - Siemens.pdf. - http://m.energy.siemens.com/ru/ru/renewable-energy/solar-power/index.htm (дата обращения: 10.01.2019).
Сологубов, А.Ю. Управление автономными гелиоэнергетическими системами: результаты расчёта параметров суточного движения Солнца в Челябинске / А.Ю. Сологубов, И.М. Кирпичникова // Альтернативная энергетика в регионах России «АЭР-2018». - 2018. - P. 279-283.
Sologubov, A.Y. Calculation of the Parameters of the Daily Movement of the Sun. Contour Maps of Kinematic Parameters / A.Y. Sologubov, I.M. Kirpichnikova // 2019 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM). - 2019. - P. 1-6.
DOI: 10.1109/icieam.2019.8742935
ESRL Global Monitoring Division - Global Radiation Group.pdf // NOAA Solar Calculator. - 2017.
Sensing and control strategies in tracking solar systems / D. Moga, I.-V. Sita, N. Stroia et al. // Proceedings - 2015 20th International Conference on Control Systems and Computer Science, CSCS 2015. - 2015. - P. 989-995.
DOI: 10.1109/cscs.2015.143
Толмачёв, В.А. Синтез следящего электропривода оси опорно-поворотного устройства / В.А. Толмачёв // Известия высших учебных заведений. Приборостроение. - 2008. - Т. 51, № 6 (Темат. вып.). - P. 68-72.
Computing the solar vector / M. Blanco-Muriel et al. // Solar Energy. - 2001. - Vol. 70, no. 5. - P. 431-441.
Michalsky, J.J. The Astronomical Almanac's algorithm for approximate solar position (1950-2050) / J.J. Michalsky // Solar Energy. - 1988. - Vol. 40, no. 3. - P. 227-235.
DOI: 10.1016/0038-092x(88)90045-x
Grena R. An algorithm for the computation of the solar position / R. Grena // Solar Energy. - 2008. - Vol. 82, no. 5. - P. 462-470.
DOI: 10.1016/j.solener.2007.10.001
Sun Tracking Systems: A Review / C.-Y. Lee et al. // Sensors. - 2009. - Vol. 9, no. 5. - P. 3875-3890.
Gibbs, P. What is the term used for the third derivative of position? / P. Gibbs. - http://math.ucr.edu/ home/baez/physics/General/jerk.html (дата обращения: 10.01.2019).
Prinsloo, G., Dobson R. Solar tracking - Sun Position, Sun Tracking, Sun Following / G. Prinsloo, R. Dobson. - Stellenbosch: SolarBooks, 2015. - 542 p.
Ray, S. Calculation of Sun position and tracking the path of Sun for a particular geographical location / S. Ray // International Journal of Emerging Technology and Advanced Engineering. - 2012. - Vol. 2, no. 9. - P. 81-84.
Дикусар, Н.Д. Полиномиальная аппроксимация высоких порядков / Н.Д. Дикусар // Математическое моделирование. - 2015. - Т. 9, № 27. - P. 89-109.
Климатические особенности Челябинской области. Обзор по месяцам. - http://www.chelpogoda.ru/pages/346.php (дата обращения: 10.01.2019).
Климат: Челябинск. - https://ru.climate-data.org/азия/россииская-федерация/челябинская-область/челябинск-463/ (дата обращения: 10.01.2019).
Оптимизация двухосевой системы слежения за Солнцем / М.В. Китаева, А.В. Охорзина, А.В. Скороходов, А.В. Юрченко // III Научно-практическая конференция «Информационно-измерительная техника и технологии». - 2012. - P. 114-124.

Еще

Статья научная