Кинематический синтез кривошипно ползунных механизмов 3-го класса при заданных положениях рабочего органа в момент выстоя и его направляющей

янию, откладываемому от точки W пересечения перпендикуляра ОW с направляющей NN .

Осуществим графическое построение кривошипно-ползунного механизма 3-го класса с вы-стоем выходного звена при заданных условиях.

Введем правую систему координат хОу машины-автомата, началом О которой является центр распределительного вала. Проводим под углом a к оси абсцисс Ох прямую, проходящую через начало координат, и откладываем отрезок OW равный d_N в абсолютных единицах. Построим нормаль NN к линии OW , и таким образом, зададим положение направляющей выходного ползуна. Для идентификации положений точки С^* относительно прямой ОW введем целочисленный параметр i , который принимает значение, равное 1, если поворот на острый угол отрезка OW вокруг точки O к отрезку OС^* , будет наблюдаться против часовой стрелки, и равным –1 в противном случае.

От точки W делаем засечку в заданном направлении длиной d_С и находим требуемое положе-

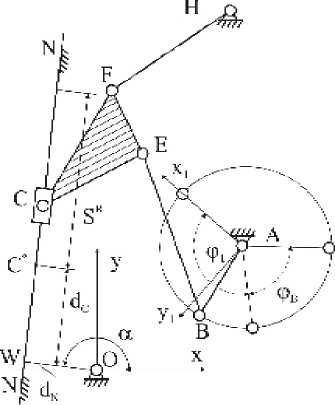
Рис. 1. Схема механизма 3-го класса ние С* рабочего органа цикловой машины-автомата в момент приближенного выстоя (рис. 2).

Построение схемы ползунного механизма 3го класса первоначально ведется в некоторой дополнительной правой системе координат x₁Аy₁ , начало которой совпадает с центром А вращения кривошипа, а ось абсцисс – с положениями кривошипа АВ⁰ и шатуна В⁰Е⁰ в момент мгновенной остановки выходного звена механизма (рис. 3). Такое расположение системы координат позволяет упростить выражения для проекций шарниров на оси системы координат. Графический синтез механизма на этом этапе ведётся в относительных единицах, что позволит затем масштабировать чертеж, с тем чтобы обеспечить соизмеримость относительных размеров проектируемого механизма с конструктивными размерами цикловой машины-автомата.

Примем длину кривошипа АВ за единицу и отложим ее приемлемым для графических построений отрезком (рис. 3). Вычертим положе-

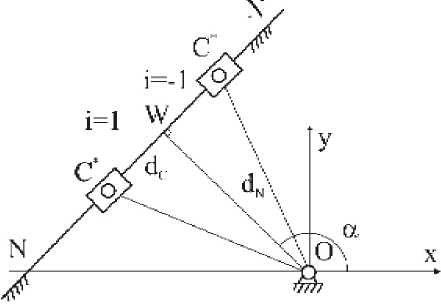
Рис. 2. Последовательность построения положений направляющей ползуна и выходного звена в момент выстоя в абсолютных единицах в системе координат машины-автомата ния AB0, AB1 и AB2 кривошипа AB. Проведем линию VV, совпадающую с биссектрисой угла jВ. Назначив относительную длину b шатуна BE, найдем положения E1 и E0 точки E в начале и в конце выстоя конечной продолжительности и при мгновенной остановке выходного звена в другом крайнем положении. Откладываем угол 02, определяющий положение точки EUU, - предельное положение шарнира E на интервале выстоя, относительно VV. При этом хорда g будет соединять точки E1 и EUU. Проведем серединный перпендикуляр ММ к отрезку ЕUUЕ1, затем из точки E1 заданной относительной длиной е звена CE делаем засечку на прямой ММ, таким образом вычерчиваем положение точки С1 шарнира C в системе координат х1Ау1, который должен для достижения наилучшего равномерного приближения располагаться в одном и том же положении в начале и в конце интервала выстоя и в момент, когда кривошип AB и шатун BE оказываются в интервале выстоя на одной линии.

Совмещая начала координат О и А систем хОу и х₁Ау₁ , поворачиваем оси последней так, чтобы сначала совпали прямая АС¹ с линией ОС^* , а затем, масштабируя проектируемую схему механизма (рис. 3), обеспечиваем совпадение точек С¹ и С^* (рис. 4). Для перехода от относительных единиц, в которых построен механизм, к абсолютным размерам машины-автомата рассчитываем коэффициент масштабирования:

Ц = l c * / l c i , (1) где l_C* – расстояние от начала координат О в системе координат хОу до точки С^* , соответствующей заданному положению рабочего органа машины-автомата; l_C1 – расстояние от опорного шарнира А в системе координат х₁Ау₁ до точки С¹ выходного ползуна в момент приближенного выстоя, находятся по формулам:

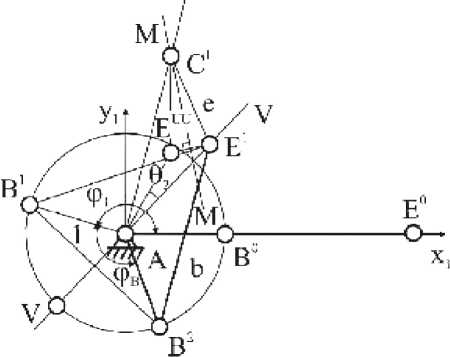
Рис. 3. Последовательность построения ползунного механизма 3-го класса в дополнительной системе координат х₁Ау₁ в относительных величинах

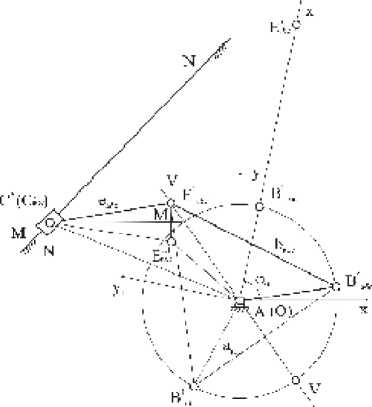
Рис. 4. Совмещение систем координат хОу машины-автомата и х₁Ау₁ проектируемого механизма

l c . = V Nl + Cl ; l c 1 = V ( x« н ) ² + ( у" " ) ² .

Дальнейшие построения ведутся в абсолютных координатах с учетом скорректированных положений центров шарниров В, Е и С , а также абсолютных значений кинематических параметров а, b и е .

абс       абс хЕ 1     уЕ 1

абс       абс хЕUU  yЕUU абс       абс х Е0    уЕ0

абс       абс

. ^хС 1       ^уС 1

отн х Е 1

отн х ЕUU

отн х Е 0

х

отн

C 1

отн уЕ 1

отн yЕUU отн уЕ 0

отн уС 1

Ц cos ( ^ 0 ) ^Х[ ц sin ( ф о )

- A sin ( ^ 0 ) Ц cos ( ^ 0 )

где ( Х абс , у . абс ), ( х О^тн , у .О™ ) — координаты центров шарниров ползунного механизма 3-го класса с приближенным выстоем выходного звена в аб-

солютных и относительных единицах соответственно; ф ₀ - угол между осями абсцисс Ах 1 и Ох , при котором прямые АС₁ и ОС_* совпадут (рис. 3).

Задаем угол h и длину f стороны CF базового звена ECF и вычерчиваем положения F¹ и F^UU шарнира F . Для построения звена CE в положении C⁰E⁰ , соответствующем началу циклограммы, делаем засечку на линии NN из точки Е⁰ длиной e_абс , равной произведению принятого ранее относительного значения на коэффициент масштабирования (1). Откладывая угол h от отрезка C⁰E⁰, вычерчиваем положение E⁰C⁰F⁰ базового звена ECF. Шарнир F является шатунным шарниром промежуточного коромысла FH . По трем положениям F⁰, F¹ и F^UU шарнира F звена FH , которые находятся из условий построения граничных положений механизма [1, 3], графически находим центр H его вращения как точку

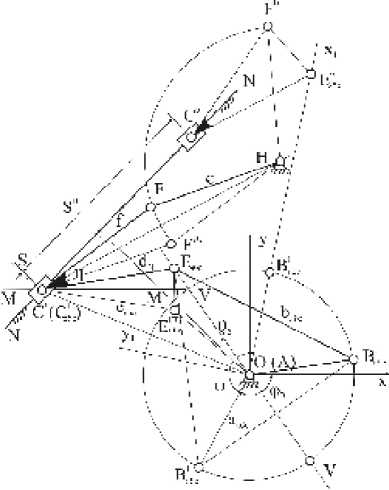
Рис. 5. Кинематическая схема кривошипноползунного механизма 3-го класса с выстоем выходного звена

пересечения двух серединных перпендикуляров, восстановленных к отрезкам F¹F^UU и F⁰F¹ .

Данный алгоритм графического построения кривошипно-ползунных механизмов 3-го класса с выстоем выходного звена позволяет синте-

зировать механизм при заданных циклограмме, положениях рабочего органа в момент приближенного выстоя и его направляющей, а также назначить начальные значения свободных кине-

матических параметров.

Разработка аналитического метода синтеза рычажных кривошипно-ползунных механизмов 3-го класса основывается на общих положениях синтеза механизмов с выстоем, представленных в работах [1, 2]. На основе построенной кинематической схемы кривошипно-ползунного механизма 3-го класса с приближенным выстоем выходного звена (рис. 5) получим методом проекций аналитические зависимости для расчета вычисляемых кинематических параметров.

При кинематическом синтезе проектируемого механизма в качестве назначаемых выступают параметры циклограммы: ф 1 , ф в , парамет-

ры направляющей: d_N и a , а также положение С^* рабочего органа машины-автомата в системе координат хОу , которое задается расстоянием d_С . Свободными параметрами синтеза в данной работе приняты: b, е и f – соответственно относительные длины звена ВЕ и сторон СЕ и СF треугольного звена ЕСF ; h – угол между сторонами EС и СF звена ЕСF ; q₂ – угол, задающий крайнее положение С₁E_UUF_UU звена СEF относительно положения С₁E₁F₁ этого звена в начале выстоя конечной продолжительности.

Предлагаемый метод кинематического синтеза механизма 3-го класса с выстоем позволяет, с использованием известных тригонометрических методов, получить аналитические зависимости для рассчитываемых параметров механизма: m и с – коэффициента масштабирования и длины коромысла СН соответственно, а также кинематические характеристики схемы: S^R – абсолютное перемещение выходного звена механизма за интервал движения; S¹ – кинематическую точность позиционирования ползуна на интервале приближенного выстоя.

Уравнение направляющей NN в системе координат хОу с угловым коэффициентом записываем как:

у = - ctg ( a ) х + ( sign ( N N ) • N N )/ sin ( a ) . (3)

Определяем координаты ( x ^'^н , у Ет^н ), ( X euu , у⁰ Ёии ) и ( Х ео ^н , у° Ё0^н ) положений Е¹ , Е^ии и Е⁰ точки Е в системе x₁Аy₁ :

х Ё'^н = h cos(6 1 ); x EUU = ( b - a ) cos(6 1 + 6 2 ); ^уЁ^т н = h sin( 6 1 ); у ЁЦНи = ( b - а ) sin( 6 1 + 6 ₂);

x ЕЕ° = a + b;У ЕТН = 0,

где h = [ b ² - a ² • sin² ( °’5 ф _в ) ] °’⁵- a • cos ( °’5 ф _B ) ;

01 = ф1 + 0.5фв - п.

Рассчитаем координаты ( x _C ^от ₁ ^н , y _C ^от ₁ ^н ) шарнира С в момент начала выстоя как точку на серединном перпендикуляре ММ к отрезку g , соединяющему точки Е¹ и Е^UU :

Имея ввиду, что центр вращения Н промежуточного коромысла НF лежит на пересечении перпендикуляров, восстановленных из середины хорд F⁰F¹ и F¹F^UU , найдем координаты ( х_Н, у_Н ) центра Н в системе координат x₁Аy₁. Запишем уравнения прямых F⁰F¹ и F¹F^UU соответственно как:

^У = k F ° F 1 "  ^{Х + b}F ° F 1 ; ^У = k F 1 FU "  ^{Х + b}F 1 FU ,

где k F ° F 1 = ^{( У}Е 1 ^УЕ ° )/⁽ x F 1

^b F ° F 1    ^У Е °    ^X F ° "  ^k F ° F 1 ;

Х отн = х Етн - е cos ( e ) ;

У™ н = У ЕТн + e sin ( e )

где

^k F 1 FU = ^{( У} Е 1 ^У Еи )/^{( X} F 1

е = arcsin (( b - a ) sin ( 0 ₂ ) / g ) - 0 1 + arccos ( °.5 g / e ) ;

g = [(b - a )2 + h2 - 2(b - a)h cos(02)] °’5 •

Совместив системы координат хОу и х₁Ау₁ , определим угол j₀ , на который необходимо повернуть плоскость, связанную с механизмом, так чтобы прямая АС¹ совпала с линией ОС^* в системе машины-автомата. Запишем уравнения выше упомянутых прямых с учетом выражения (3) следующим образом:

У АС 1 = ( Уп с/ х абхс ) • Х ас 1 ; У ос * = tg ^{(а - в} ) •

x OС *^;

где в = arctg ( d _c /d_N ) •

Рассчитаем угол j₀ между осями абсцисс Ах₁ и Ох :

абс абс                       абс абс sign(yc 1 /ХС1   tg (а в )) (уС 1 /ХС1   tg (а в))

1 + ( У С 1 с/ х С 1 с ) • tg ( а - в )              ,

Вычислив коэффициент масштабирования m по формуле (1), определяем абсолютные значения длин кривошипа АВ , шатуна ВЕ и стороны ЕС треугольного звена CEF :

аабс = М; ba6e = М" b; еабс = М" е-

Положение С⁰ выходного ползуна С в системе координат х₁Ау₁ в момент мгновенного выстоя найдем из системы уравнений, составленной исходя из того, что точка С⁰ лежит на прямой NN (3) и расстояние между центрами шарниров Е и С равно е_абс :

У с ° = - etg ( а - ф ° ) Х с ° + d N / sin ( а - ф ° ) ; абс ²                 абс ² 0.5

^е абс = LV x C °    ^Х Е ° / ⁺ V^е °    ^Уе ° / J ’

где x _E ^аб ₀ ^с и y _Е ^аб ₀ ^с вычислим по формуле (2).

Координаты ( х_F1, у_F1), (х_F0, у_F0) соответственно точек F¹ и F⁰ шарнира F треугольного звена

CEF , рассчитаем формулам:

X f 1 = х Сбс + f cos e + п+п\         У F 1 = У Сб^с + f sin e + п+п\

X f ° = Х с ° + f cos e - п ) ;        У е ° = У с а - f sin e - п ) ,

где 8° = arccosf еабс +(+ ba6e )2 ■ С

(     ^{2 е} абс ⁽ « абс ⁺ ^бс )    )

l c ° = V ^Х с ° ⁺ у с ° •

^XF ° ^{) ;}

x FU ^{) ;}

b F 1 FU = ^У Еи x FU "  k F 1 FU ^;

Xfu = Х с 1 - (( X c 1 - Xeuu ) cos ( n ) - ( У с 1 - У EUU ) sin ( n )) f ;

e

f

У еи = У С 1 ^{-(( X}C 1 - ^Xeuu ^{) s}in ( n ⁾ + ⁽ У С 1 - У Еии ko^ n ))- ■ e

Тогда координаты ( х_Н, у_Н ) центра Н определим как решение системы уравнений:

f ^УН = ^- k_F° F 1 "  ^ХН ⁺ °’⁵ I ^УН = ^{- k}F 1 FU "  ^ХН ⁺ °’⁵

^{( k}F°F 1 " ^{( X}F ° ^{+ X}F 1 ) ^{+ У}Е ° ^{+ У}Е 1 ) ;

^{1 ( k}F 1 FU " ^{( X}F 1 ^{+ X}FU ^{) + У}Еи ^{+ У}Е 1 ) ;

В результате

xH

Ъ • к

H   F 0 F 1

. к , F 1 FU

^{/ ( k}F 1 FU

-

^kF ° F 1 ^

^УH = ^kF ° F 1 "  ^ХН ⁺ °’5 ( ^kF ° F 1 " ^{( X}F ° ^{+ X}F 1 ^{) + У}Е ° ^{+ У}F 1

где bH = °’5(kF0 F1 "(XF ° + XF1)-kF1 FU "(XF1 + XFUU ) + УЕ ° - УЕи ).

Запишем зависимости для расчета абсолютных длины c про-межуточного коромысла НF , межцентрового расстояния d_Н (рассто-яние между точками Н и А ) и малого перемещения S¹ выходного звена за интервал выстоя:

c = [(Xh - Xf ° )2 + (Ун - Уе ° )2] ’ ; dH =[xH + уН ] °’5;

S1 =[(c + f )2 - dHс]  -

-

x

H

- Х Сбс ) ² + ( У н

-

абс 2       2   0.5 , ус 1 )    ЬНС'

где d _HC = |cos ( a ) x _H + sin ( а ) y _H - d _N |.

Абсолютная величина рабочего хода S^R вы-

ходного звена механизма определяется следующей зависимостью:

S R = [ ( Х с ° - Х Сб^с ) ² + ( У с ° - у сбс ) ² ] °5 + °’5 S ¹ .

Найдем углы r₁ и r₂ , устанавливающие соответственно положения эксцентриситета l_С и отрезка d_Н относительно оси Аx₁ :

Р 1 = sign ( - У с ) • arccos ( x_c /С_с ) ;

р ₂ = sign ( ф ° - arccos ( x _H jd_H )) х х ( ф ° - arccos ( x _H / d _H )) ,

где l _C = ( d NN + d C ) 0.5 .

Определим угол d , фиксирующий коромысло HF относительно вспомогательной системы координат x₁Ay₁ :

5 = 180 o - sign ( x _F0 ) • arccos ( x F 0 / c ).

В настоящей статье разработан метод кинематического синтеза механизмов 3-го класса с возвратно-поступательным движением выходного звена и его выстоем в одном из крайних положений, позволяющий сонаправлено с графическим методом проектировать механизмы по заданным циклограмме, положениях рабочего органа в момент выстоя и его направляющей. Аналитический аппарат синтеза механизмов 3-го класса предопределен алгоритмом их графического построения, что значительно упрощает процесс получения математических моделей и проверку их адекватности.