Кинематический способ нахождения полной кривизны плоской кривой

На стыке дифференциальной и дискретной геометрии в последние десятилетия появилась новая область – дискретная дифференциальная геометрия. В то время как в классической дифференциальной геометрии исследуются гладкие геометрические объекты, дискретная дифференциальная геометрия изучает геометрические объекты, образованные конечным количеством простейших элементов, и ставит целью разработку дискретных эквивалентов понятий и методов классической дифференциальной геометрии. Последняя, в свою очередь, вновь возникает как непрерывный предел своей дискретизации при стремлении к нулю размеров дискретных ячеек. Данная область геометрии вызывает интерес не только важными теоретическими приложениями, но и своими связями с компьютерной графикой.

Дискретные объекты могут быть измерены (длина, площадь и т.п.) и могут взаимодействовать с другими дискретными объектами (сочетание/взаимодействие). Одним из важных свойств кривых и поверхностей является кривизна, с которой в дифференциальной геометрии связано множество теорем. В этой статье мы рассмотрим полную кривизну дискретных кривых на плоскости, вычисляя её в среде программирования FMS Logo.

Классическими достижениями дискретной дифференциальной геометрии являются фундаментальные результаты А.Д. Александрова [7] и А.В. Погорелова [9]. Ранний период развития отражен в работах Зауэра [6]. Работы А.И. Бобенко и У. Пинкаля [1], [2], А. Доливы и П.М. Сантини [3], [4] положили начало современному периоду.

Геометрия плоской кривой

Рассмотрим плоскую кривую: если она является достаточно гладкой, то предельное положение секущей PQ называется касательной (рис. 1). Из всех прямых, проходящих через Р , касательная – локальная аппроксимация кривой в данной точке.

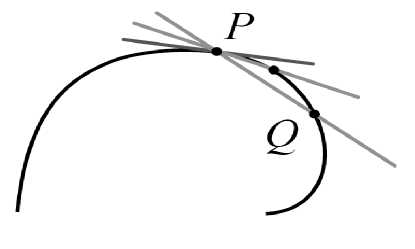
Рис. 1 Касательная к кривой в точке Р

Направляющий вектор касательной к кривой в точке P(t) будет вектор r’(t). Если s – dr естественный параметр кривой, то вектор t(s) =    – единичный вектор касательной.

ds

dt   d2r                                                              d2r

Вектор = называется вектором кривизны кривой, а его длина k ( s ) = ds   ds ²                                                               ds ²

кривизна данной кривой. Геометрически вектор кривизны можно рассматривать как скорость вращения касательной – направление и резкость изгиба кривой. Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения, отрицательный, если вращение по часовой стрелке.

В 1825 г. Карл Ф. Гаусса представил новый инструмент для осмысления формы кривых и поверхностей. Идея Гаусса состоит в отображении кривой на единичную окружность: для любой точки P принадлежащей кривой в отображении Гаусса – единичной окружности, присваивается точка Q , а именно точка, для которой радиус-вектор коллинеарен с вектором нормали в точке Р (рис. 2). Отметим, что нормаль в Р параллельна с радиусом окружности и касательная к кривой в точке Р параллельна касательной к окружности в Q . Свойства касательной и параллельности используются для упрощения важных определений в дифференциальной геометрии.

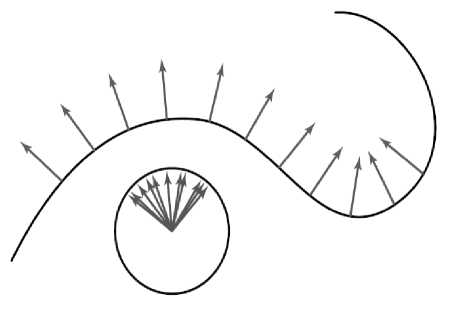
Рис. 2. Отображение Гаусса присваивает каждой точке на кривой соответствующую точку на единичной окружности

Рассмотрим образ кривой при отображении Гаусса: образом кривой является объединение всех точек на единичной окружности, соответствующих всем точкам на 21 9

заданной кривой. Для «открытых» кривых отображением Гаусса могут быть дуги или единичные окружности. Для замкнутой плоской кривой: образ всегда единичная окружность. Если кривая самопересекается, то мы можем подсчитать, сколько раз изображение полностью «обтекает» единичную окружность: это число поворотов или индекс вращения , обозначается k . Индекс равен единице, если кривая простая и замкнутая, с поворотом против часовой стрелки. Она равна нулю или ± 2 для кривой, которая самопересекается один раз, в зависимости от способа поворота и от наличия или отсутствия витков (рис.3).

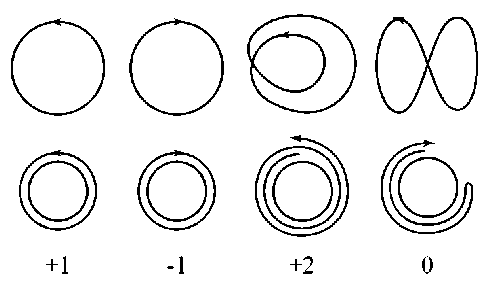
Рисунок 3 Верхний ряд: Две простые кривые с противоположными способами обхода, и две самопересекающиеся кривые, одна из которых "отменяет" поворот. Нижний ряд: гауссовское изображение кривых и связанные с поворотами индексы вращения

Неважно, сколько изгибов совершает кривая, если мы не изменим число поворотов, то не изменится полная кривизна .

b j k (s) ds = 2nk .                                 (1)

a

Чтобы изменить полную кривизну кривой нужно скорректировать кривую путем введения (или удаления) самопересекающихся петель.

Геометрия дискретной плоской кривой

Пусть дана плоская кривая r , аппроксимируем её вписанной ломаной p. Вписанной ломаной называется последовательность вершин, V 1 , V 2 ,…V n , отсортированных по обходу кривой, и отрезков, соединяющих соседние вершины (рис.4).

Полная кривизна (дискретная) вписанной ломаной вычисляется по формуле:

tsc(p) = ^ ai , i=0

где a i - это угол поворота вершины V , , взятый со знаком «-», если поворот по часовой стрелке (рис.5); если р - незамкнутая ломаная, то a ₀ = a _n = 0 . Опять же мы можем выразить полную кривизну непрерывной кривой, вычисляя предел по возможным вписанным ломаным: tsr ( r ) = sup tsr ( p ) .

p ^ r

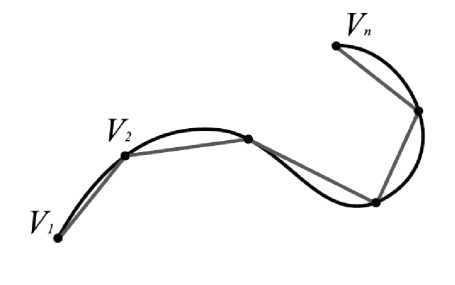
Рис. 4. Аппроксимация кривой вписанной ломаной

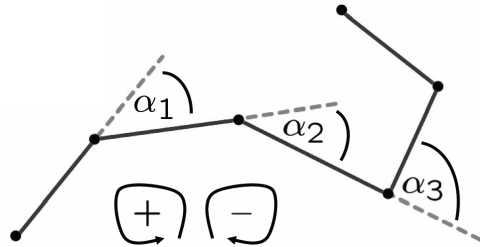
Рис. 5. α i – углы поворота вершин ломаной

Способ нахождения полной кривизны, использующий верхний предел, не очень хорошо подходит для вычислений. Построим бесконечную последовательность вписанных ломаных р 1 , р 2 , р 3 … .

Определим геометрический размер сетки р по длине его максимального отрезка:

h ( p ) = max d ( V , , V_t + 1 ) .

0 < i <  n

Предположим, что r является гладкой простой кривой. Гладкость подразумевает, что для каждой точки на кривой имеется уникальная вполне определенная касательная. Тогда можно показать, что данная последовательность р 1 , р ₂ , р₃... такая, что tsr ( r ) = lim tsr ( p ) .

Рассмотрим отображение Гаусса для замкнутой ломаной р . Каждая вершина ломаной имеет две касательные (таким образом, и две нормали), в зависимости от направления, из которого берется предел. Определим отображение Гаусса р путем назначения для каждой вершины V i дуги на единичной окружности, концами которой являются две нормали. Каждая точка принадлежащая ребру, отличная от вершины, имеет единственную нормаль и соответствует в гауссовом изображении началу или концу дуги, соответствующей соседним вершинам. Способ обхода вдоль ломаной соответствует способу обхода вдоль дуги гауссова изображения. При этом индекс вращения для гладкой плоской кривой переносится естественным образом на дискретные аналоги.

Проверим теорему об индексе вращения для дискретных кривых. Сумма внешних углов простого многоугольника 2π . Это замечание может быть обобщено, чтобы показать, что tcr(p)=2π k , где k индекс вращения ломаной. Подчеркнем, что теорема не утверждает, что полная кривизна сходится к числу, кратному 2π в пределе для ломаной, теорема справедлива для любого (сколь угодно грубого) многоугольника. Однако следует отметить, что индексы вращения для кривой и ломаной могут не совпадать, по крайней мере, пока вершин недостаточно много (в нужных местах) для оценки топологии кривой.

Кинематический способ нахождения полной кривизны плоской кривой

Рассмотрим нахождение полной кривизны некоторых кривых в среде программирования FMS Logo.

Пусть кривая r - это окружность, заданная уравнением x= cos t, y= sin t , t e [0;360] .

Впишем ломаную, имеющую 10 вершин, и составим список, состоящий из координат данной кривой.

это таб пусть "pol [ ]

для [t 0 360 36][вочередь "pol список произведение 100 cos :t произведение 100 sin :t] вд :pol конец

Далее находим полную кривизну как сумму углов поворота ребер ломаной. Процедура для нахождения полной кривизны окружности:

это кривизна пусть "pol таб

Пусть "ug []

пп для [t 1 11 1][нм элемент :t :pol по жди 5]

пп для [t 1 10 1][нм элемент :t :pol вочередь "ug внаправ элемент сумма :t 1 :pol новыйкурс элемент :t :ug жди 45]

пусть "k 0

пусть "ug1 []

повтори 9[вочередь "ug1 разность элемент сумма счетчик 1 :ug элемент счетчик :ug]

пусть "k 0

повтори 9 [пусть "k сумма :k Элемент счетчик :ug1]

пш сумма :k разность элемент 1 :ug сумма элемент 10 :ug 360

конец покажи :ug

[342 306 270 234 198 162 126 90 54 18]

В списке :ug углы, образуемые ребрами многоугольника с осью Oy .

покажи :ug1

[-36 -36 -36 -36 -36 -36 -36 -36 -36]

В списке :ug1 углы поворота Тортилы в вершинах многоугольника.

При вызове процедуры <кривизна> получаем результат -360 , при этом видно, как поворачивается Тортила, рисуя многоугольник (рис.6).

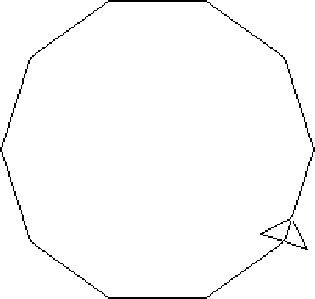
Рис. 6 Дискретная окружность

Т.к. поворот осуществляется против часовой стрелки, следовательно, результат получается с отрицательным знаком.

Индекс вращения окружности равен единице (знак выбирается в зависимости от способа обхода), следовательно, согласно формуле (1) полная кривизна окружности равна 360.

В таблице 1 показаны результаты вычисления полной кривизны некоторых замкнутых кривых (строки 1-3) в среде программирования FMS Logo.

Если кривая не замкнута, то, применяя процедуру, используемую для окружности, можно вычислить полную кривизну таких кривых. Например, для синусоиды, заданной п уравнением y = 100 sin у^ x, полная кривизна оказывается равной нулю. А если рассмотреть параболу y = X2, полная кривизна равна -176.143199 (строки 4, 5 табл.1).

№	Название	Полная кривизна	Индекс вращения	Изображение
1	Кардиоида f x = 100cos t (1 + cos t ) [ y = 100sin t (1 + cos t )	-360	1
2	Астроида x = 100cos 3 1 y = 100sin 3 1	-360	1
3	Лемниската Бернулли 3 t + t l x = 1001 + 1 * I ' = '< 1 4	0	0
4	Синусоида П y = 100sin--- x 180	0	-
5	Парабола y = x 2	-176.143199	-