Кинематика очага деформации при безоправочной прокатке труб нефтяного сортамента

В состав большинства современных трубопрокатных агрегатов (ТПА) входят станы для без-оправочной прокатки. К таким станам относятся редукционно-растяжные (РРС), извлекательно-калибровочные (ИКС). РРС позволяют увеличить сортамент производимых на ТПА труб за счет дополнительного обжатия по наружному диаметру до 70 %, ИКС помимо обжатия по наружному диаметру, также выполняет функцию извлекателя оправки раскатного стана.

Наибольшее распространение получили непрерывные многоклетьевые двух- или трехвалковые станы безоправочной прокатки. Так как они обладают наибольшей технологической гибкостью, достаточно легкой настройкой и имеют простую конструкцию. При этом зачастую используется овальная форма калибров. Такой калибр полностью определяется значениями ширины и высоты калибра, которые в свою очередь определяются значением овализиции и величиной обжатия по

наружному диаметру.

При известных ширине А и высоте В калибра радиус калибра R _к для трехвалковой клети составит:

R к

A2 - AB + B 2

A - 2 B

e = R k — B .                                  (2)

Математическое описание процесса прокатки труб на таких станах является важной задачей, поскольку позволит решить ряд задач, таких как определение формоизменения металла в процессе прокатки, энергосиловых параметров и т. п.

В первую очередь при разработке математической модели решаются геометрическая и кинематическая задачи. Известна методика определения геометрических и кинематических параметров очага деформации в декартовой системе координат [1]. Однако ввиду существенной нелинейности заготовки и калибра, при этом получаются достаточно сложные математические зависимости. Гораздо проще вопрос решается в цилиндрической системе координат. Решение геометрической задачи подразумевает символьное определение следующих параметров очага деформации: наружный диаметр трубы d или радиус r в любом сечении очага деформации, длина очага деформации l , угол захвата a ₀ (рис. 2).

Общеизвестно, что:

l = V R _B( d 0 - d i );                              (3)

Эксцентриситет калибра е составит при этом (рис. 1):

ao =

d 0 — d 1

R в

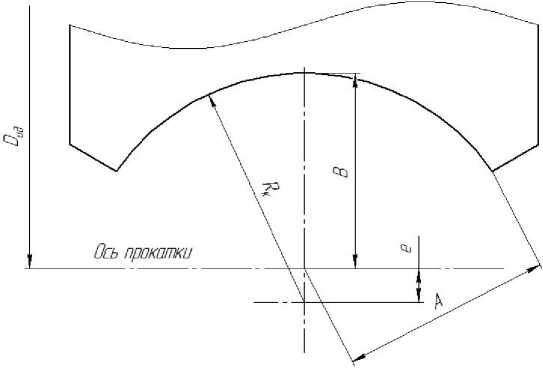
Рис. 1. Схема калибра

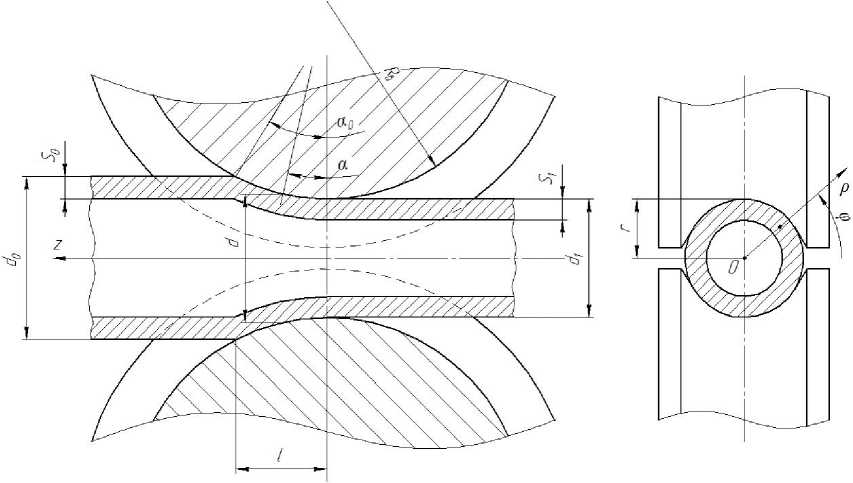
Рис. 2. Схема очага деформации

В соответствие с введенной цилиндрической системой координат наружная поверхность на выходе из очага деформации описывается функцией:

р = д/ R К2 - e ² cos ² ф - e sin ф . (5)

В данном случае р будет являться наружным радиусом трубы. Поскольку двухвалковый калибр имеет две оси симметрии, а трехвалковый – три, то для двухвалкового можно рассматривать четверть очага деформации фе [ 0; л/ 2 ] , для трехвалкового -шестую часть: фе [ л/6; л/2 ] .

Наружная поверхность трубной заготовки в цилиндрической системе координат описывается функцией:

Р = r o - (6)

Наружная поверхность валка выражается из уравнения тора:

р sin ф =

Совместное решение уравнений (6) и (7) позволяет определить поверхность контакта металла трубной заготовки с валками первой клети, а совместное решение уравнений (5) и (7) – для последующих клетей. Однако при этом необходимо учитывать, что валки каждой клети развернуты относительно соседних на угол: для двухвалковых клетей - л/2, для трехвалковой - л/3 . То есть при решении системы уравнений (5), (7) в уравнении (5) к ф прибавляется соответствующий угол кантовки.

Решение кинематической задачи при безопра-вочной прокатке труб нефтяного сортамента (тонкостенных) подразумевает построение поля скоро-

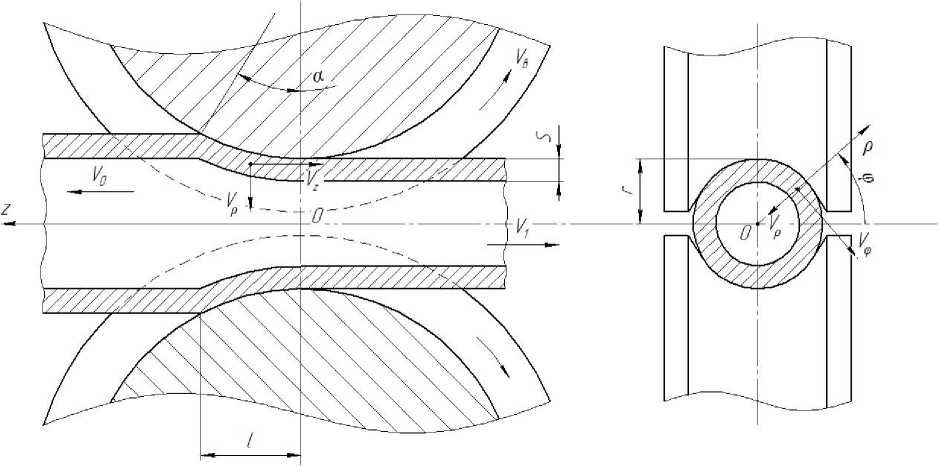
Рис. 3. Компоненты вектора скорости

стей металла трубы и определение тензора скорости деформации.

Вектор скорости в цилиндрической системе

координат может быть представлен в виде (рис. 3):

—*

V =

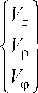
С учетом этого получим:

^Vz\_z = ₀ = a 0 = ^V 1 , т.е. a 0 = V;

2 V

V = V + al + aJ = —, т.е. ^z z = l  112 X

V ₁                  2

--V = aj + a^l ;

X

Компонента вектора скорости V_z в любом поперечном сечении очага деформации должна распределяться равномерно по этому сечению, так как в противном случае появится изгиб или кручение трубы. Поскольку считаем, что прокатный стан настроен правильно, подобные явления должны отсутствовать. Следовательно, данная компонента вектора скорости является функцией координаты z : V z = V_z ( z ).

Поскольку в продольном сечении очага деформации валок имеет форму окружности, принимаем, что компонента вектора скорости V_z изменяется вдоль очага деформации по параболическому закону, то есть

V z = a 0 + a 1 z + a 2 z 2 . (9)

из последнего равенства следует:

V (1 -X)

—       = a + a?l или l V x J 1    2

dV           dV

----= a . — 2 a 2 z ; ---- dz              dz

Для определения коэффициентов a ₀ , a ₁ и a ₂

воспользуемся следующим очевидным условием:

^V z L - . o = V ;

dVz dz z=0

где V ₁ – скорость трубы на выходе из очага де-

формации; V ₀ – скорость трубы на входе в очаг деформации; X - коэффициент вытяжки.

V (1 -x a = —1 l V X

= a 1 = 0, т. е.

z = 0

тогда

^V i ( 1 ^{— X} )                ^V ( 1 ^{— X}

0 = —      — aJ или a-, =

l V x J 2         2 l2 V x

— a 2 1 ;

.

Окончательно для V_z можно записать:

z2 (1 — XV = V + v z 1     112 V x

V z = V 1

z (X — 1 I

^1— l ²    ■

или

a 1 = 0,

При определении зависимости для V _p в отличие от поля скоростей, построенного для случая прокатки трубы на оправке [2], будем считать, что V _p = 0 при р = 0 .

По толщине стенки трубы V _p теоретически может распределяться по разным зависимостям (рис. 4). Однако ввиду рассмотрения прокатки тонкостенных труб, например, нефтяного сортамента, можно считать, что закон изменения V _p ( р ) близок к линейному, то есть

V _p = b о + b [ P , при r — 5 ^р^ r .

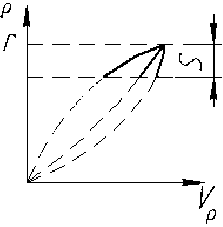
Рис. 4. Распределение компоненты вектора скорости V _ρ по толщине стенки

несжимаемости имеет вид: ^ = 0, где ^ - ско-

рость относительного изменения объема, которая является первым инвариантом тензора скоростей деформации. Следовательно, можно записать

Поскольку труба в поперечном сечении имеет симметричный профиль, компонента вектора скорости V _p при фиксированной координате р будет

где ^ _рр , ^ _фф , ^ _zz - компоненты тензора скорости деформации, расположенные на главной диагонали. В цилиндрической системе координат они вычисляются следующим образом [3]:

е = М = V . [1 ?0-1Y •

₽       W.₊ V z [1 - z 2 [M )1;

постоянной по периметру поперечного сечения. Поэтому при определении коэффициентов b ₀ и b ₁

рассмотрим меридиональное сечение трубы, соответствующее вершине калибра ( ф = л/2).

дV      2z [Л-11

z

.

дz        72 Г Л J

Из граничного условия

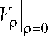
следует, что

На контактной поверхности трубы и валка вектор скорости металла трубы должен быть направлен по касательной к этой поверхности. Это, в свою очередь, определяет соотношение между компонентами вектора скорости V_z и V :

Отсюда получаем:

д V p_L 2 z [Л- 1 1 V z Г z ² [Л- 1 1 = V                      1

дф 72 Г Л J r R 72 Г Л J

V ₁ z rR

l ²

Л-1 Л

р

или

2 z [Л-1

^V p| р= r = V z tg a , ф=п т

V ф = V Ml —

l

2z rR

^1- 7 2    Л

где а - угловая координата произвольной точки на контактной поверхности (см. рис. 1).

Из простых геометрических построений следует, что а = z/R , где R - радиус валка по вершине калибра.

Поскольку при деформации труб в стане-извлекателе и редукционных станах обжатия по диаметру относительно малы (как правило, не превышают 10 %), угол а также достаточно мал, и можно принять:

z tgа ~ а = .

R

С учетом этого получаем:

.       1 [Л-1

= 2рф zV,<— ---

172 Гл,

1 rR

¹ - 7 2    Л

U C .

V   = br = V — plp=r    1 zR

z или br=V

1     1 R

z [ Л-1 ] 1—72 Ш

Следовательно

При прокатке в двухвалковом калибре прокатываемый трубный профиль имеет всегда две оси симметрии, одна из которых лежит в плоскости разъема калибра. Естественно, что благодаря этому тангенциальное течение металла в плоскости разъема калибра будет отсутствовать. Следовательно, для определения константы интегрирования С можно воспользоваться условием V p | _Q = 0 , из которого следует, что С = 0. Таким образом, окончательно для двухвалкового калибра для V _p можно записать:

V Г/ ¹ [ ^Л-1 | ¹ 1 ^{z 2} [ ^Л-1 |

V d = 2pф zV -----1—z- --- [ (12)

При прокатке в трехвалковом калибре трубный профиль имеет три оси симметрии и для него справедливо следующее: V = 0, из которого ^ф 1ф=л/ 6

Окончательно получим:

следует, что

^Р 6    ¹ 7 ²

1 rR

¹ - 7 2    Л

Компонента вектора скорости V _ф может быть определена из условия несжимаемости. Условие

Таким образом, окончательно для трехвалкового калибра для V _p можно записать:

V p = 2p

6 J 1 l ² I X

1 rR

' z ² (X —1) ^{1 —} l ² ItJ

Построенное поле скоростей двухвалкового калибра:

позволяет определить компоненты тензора скоростей деформации для

.  = V i z 1 - z_L гм) .

M 2 zV 1 J

1 । X — 1

7 It

—

1 rR

' z ² (X — 1 Y ^{1 —} l² ItJ

Vxz

? + —

rR

' z ² (X — 1 Y ^1—T² ItJ

^ zz

2 z (X — 1 )

^V 1 /2 I          J ;

l V X J

^ pV

1 ( ⁵ V ₊ 5 V p 2 V dp p-дф

V J 1 U т//¹ (X — 1 + — Ы²Ф ^zV 1( tI T p J 2 ^         l ² V X

—

1 rR

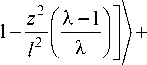
+ 0 — 2 ф zV /^^(X-Y)——

¹ \ l ² V X J rR

, z ² (X — 1 Y ^1—T² ItJ

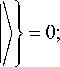
^ ф z

1 (d V_z ^{5 V} v )   1/           Г 1 (X — 1 )    1 Г z ² (X — 1 Y

-I---— + —-l=-(0 + 2 mp V 1 ' , I----I--1 —-I---- I 2 (p-дф 5 z J 2\           [ l ² V X J rR L l ² V X J

^ +

^{+ 2 ф zV} 1 ^p rRl 2

X — 1

Г ¹ ( ^{X— 1} ) =v V 1 p^ ;2 Нг I

1 1 V X J

1 rR

z ( X — 1 ।      2 z ( X — 1 11

^{1 —} l ²" X ' rR/ ² l~Jj ^;

^ z p

1 f 5 V_o QV )

¹ ^ + ⁵ V L

2 V 5 z 5p J

= ¹ ^ V -p

¹ rR

' z ² (X — 1 ) ¹—T²1~J

+ V p z Г— 21 (i— i )1+ 0 l.£ * i

¹ rR L l ² V X JJ 2 rR

1 — 3 'z^ f ^Xf1 l ² IV X

Для трехвалкового калибра компоненты тензора скоростей деформации не отличаются за исключением ^_{ф z} , которая выражается как:

^ ф z

Для численной оценки компонентов тензора скоростей деформации последние были рассчитаны для случая прокатки трубы размерами 73×6 мм из трубной заготовки 152×6 мм. На рис. 5 представлена зависимость компонентов тензора скоростей деформации для первой клети от величины обжатия и их распределение по длине очага деформации. При этом настроечные параметры использовались следующие: X = 1,03, обжатие - 3,2 %; V ₀ = 1000 мм/с .

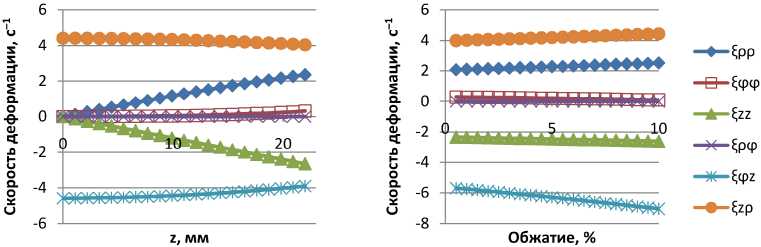
а)                                                               б)

Рис. 5. Компоненты тензора скоростей деформации: а – по длине очага деформации; б – в зависимости от величины обжатия по наружному диаметру

Как видно из рис. 5, б, компонента тензора и ^_фф значительно меньше остальных составляющих, а компонента ^_pv равна нулю, что позволяет не учитывать их в инженерных расчетах. Таким образом, определена кинематика очага деформации при безоправочной прокатке труб в двух- и трехвалковом калибрах с точностью до V ₁ .