Кинематика привода в зависимости от угловой скорости поворота платформы оригинального манипулятора

Объектом исследования является шестикоординатный манипулятор, описанный в [1, c.65], [2, с.2], [3, с.2]. Схемное решение оригинального пространственного манипулятора представлено на рис. 1.

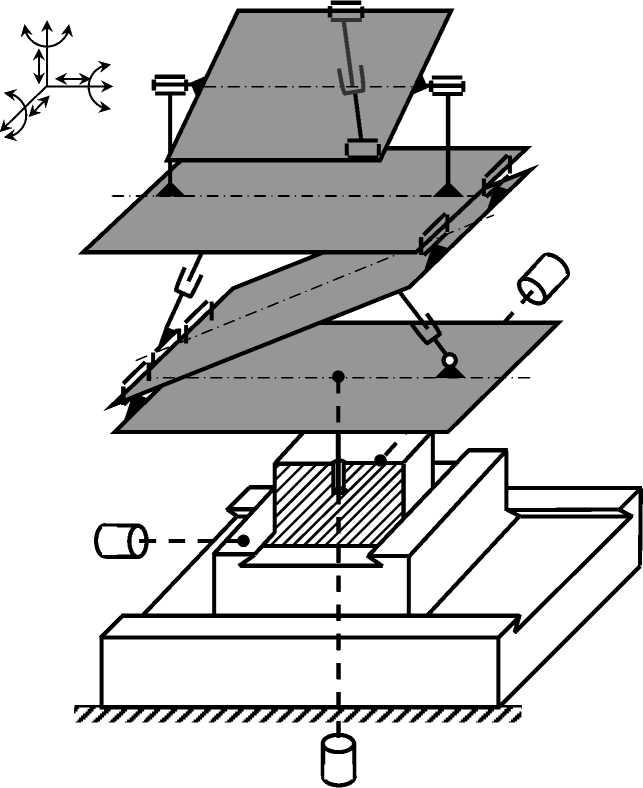
Рис. 1. Схемное решение оригинального пространственного манипулятора

Рассмотрим только фрагмент оригинальной части пространственного манипулятора, схема которого представлена на рис. 2. Как было описано ранее, оригинальность данного пространственного манипулятора заключается в создании поступательного вертикального перемещения посредством двух встречных вращений наклонной платформы 1 и опорно-поворотного стола 2, т.е. угловые скорости звеньев т1 и m2 направлены в противоположные стороны [4, с.248].

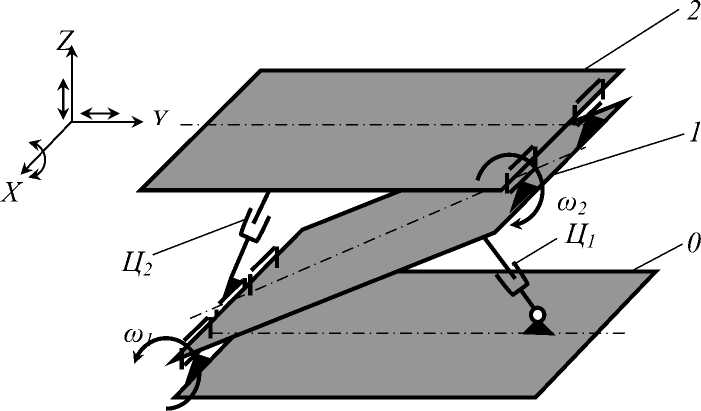
Рис. 2. Расчетная схема фрагмента оригинальной части манипулятора 0 - Основание; 1 - Наклонная платформа; 2 - Опорно-поворотное устройство; Ц1, Ц2 - Приводные устройства (гидроцилиндры).

При унификации всех приводов поступательного перемещения, расчетная схема кинематических характеристик преобразования движения сводится к моделированию соотношений в изменяемом «треугольнике», одна сторона которого изменяет свой размер и конструктивно исполнена, например, гидроцилиндром со штоком (рис. 3).

Аналогично исследованиям, которые были проведены в [5], где рассамтривалась зависимость угла поворота платформы ф от кинематки привода, рассмотрим характеристику движения m , т.е. как будет изменяться угловая скорость наклонной платформы манипулятора в зависимости от кинематических параметров привода (гидроцилиндра).

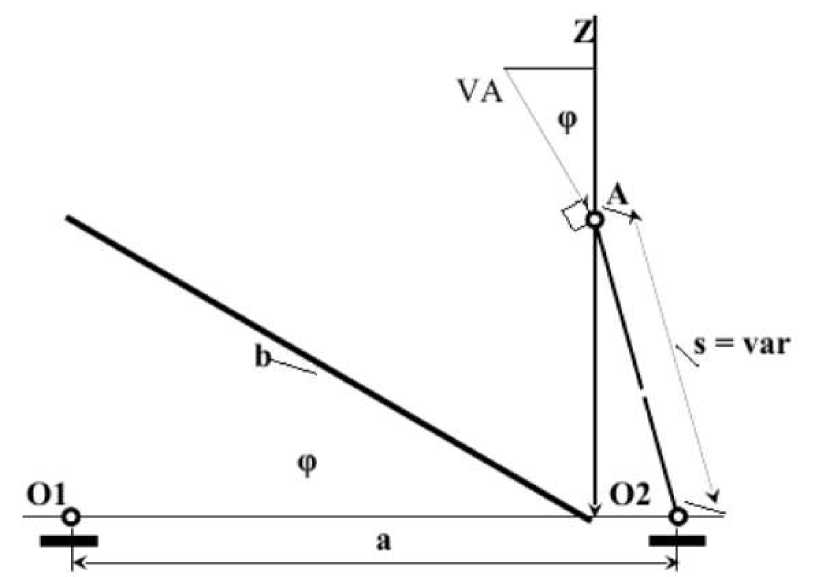
Рис. 3. Расчетная схема изменяемого треугольника механизма при s = var

s = О₂А =var – изменяемая длина штока гидроцилиндра; О₁О₂ = а = const – расстояние между опорами; О 1 А = b = const – длина наклонной платформы; φ = var – угол наклона наклонной платформы.

Здесь можно рассмотреть 2 случая:

dsds

• 1)    изменение го при V = — = const, 2) изменение го при V = — = var. dtdt

В [5] уже была найдена зависимость

V2

ф(У, 1) = arccos(1--

2 a ²

Дифференцируя выражение (1) по времени t найдём угловую скорость:

d arccos 1

—

dm к го =   = —

dt

к dt

V ²

• 1

2 a ²

-

4 1 —_r 12 dt к 2 a¹ J

-

1 - к

V ² 2 a ²

• ¹²

J

d ( V2 )

• 1+ d1 ( 2 a2 )2

• d ( 1 ²) dt

2 V + 2 V • 1

V4 a2 - V2 • 12 ’ dV где V = — = W dt

• - ускорение штока гидроцилиндра.

dV

Пусть V = const, тогда V =   = 0 и dt

^ ( a, V , t ) =

2 V

V 4 a ² - V ² • t²

IУ   dV

Если V = var , тогда ^V = ~~r = W ^ ⁰ и dt

® ( a , V , W , t ) =

2( V + W • t )

4 a ²

^“

V ² • t²

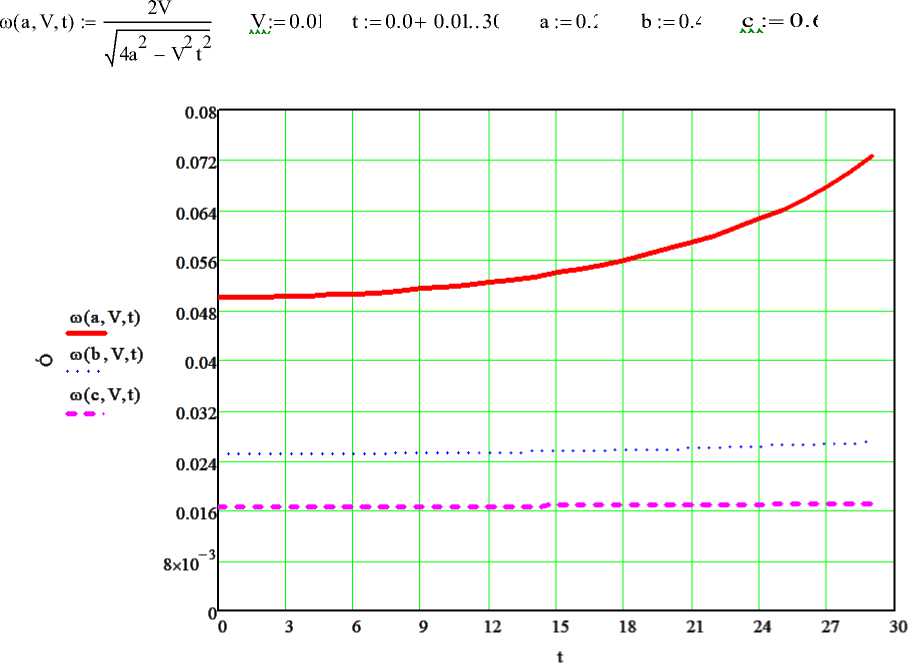
Используя пакет программы MathCAD 14, приводим зависимости выражений (2) и (3) которые представлены на рис. 4(а, б) и рис. 5( а , б ).

а)

б)

V := 0.02

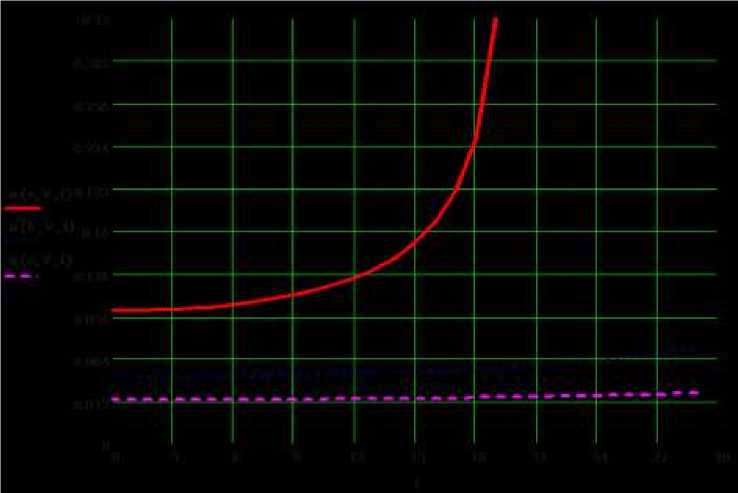
Рис. 4. Зависимости угловой скорости наклонной платформы ю(а, V, t)

от времени t = var при разных скоростях штока гидроцилиндра

а)

m (a , V , W , t) := 2 (V + W ' t)     V := 0.01 W := 0.0

t := 0.0 + 0.01 .. 30

2   22

4a - V t a := 0.:       b := 0.^      c := 0.(

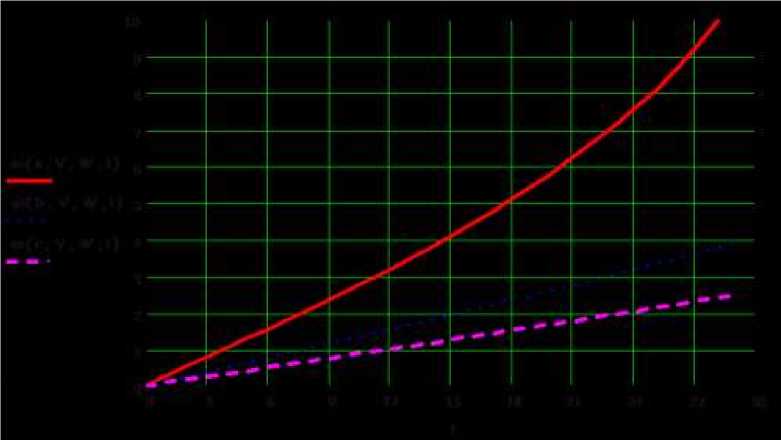
б)

V := 0.02

W := 0.0

to (a , V , W , t)

m (b , V , W , t)

to (c , V , W , t)

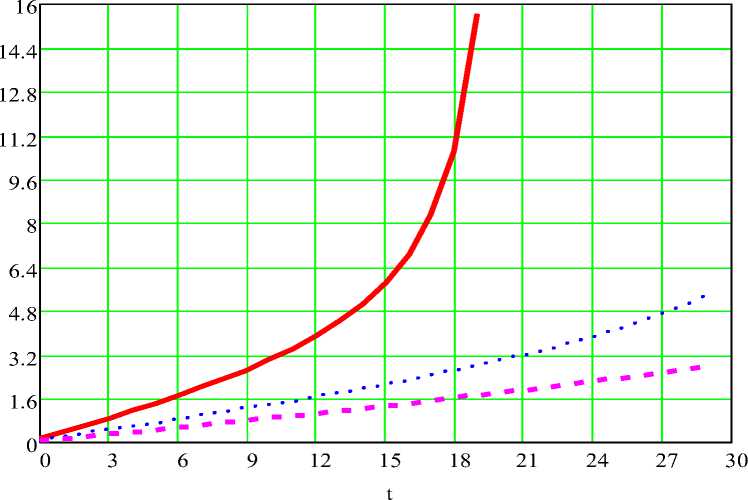
Рис. 5. Зависимости угловой скорости наклонной платформы ю(а, V, W, t)

от времени t = var при разных скоростях V штока гидроцилиндра

Выводы:

Анализируя эти графики, в зависимости от параметра V и времени t видно, что:

• 1)    С увеличением: скорости движения V и ускорения W штока гидроцилиндра поворот платформы осуществляется быстрее;

• 2)    Зависимость ro(t) при V = 0,01 м/сек и t< 6 сек , при V = 0,02 м/сек и t< 12 сек, при V = 0,03 м/сек и t< 24 сек практически линейна, что очень благоприятно при эксплуатации данного манипулятора;

• 3)    В рабочем диапазоне: ф = 0° - 45°, изменение угловой скорости наклонной платформы 1 (или опорно-поворотного устройства 2) изменяются незначительно, что благоприятно для рабочего процесса, использующего данный манипулятор.

• 4)    Чем меньше скорость движения штока гидроцилиндра, тем линейнее будет зависимость угловой скорости, т.е. она будет прямо пропорциональна времени и скорости движения штока гидроцилиндра, тем самым будут более благоприятнее условия работы манипулятора.