Кинетическая модель деактивации О2 ( а 1D)

Низкий коэффициент усиления активной среды электроразрядного кислородно-йодного лазера (ЭКИЛ) [1] не позволяет осуществлять эффективный съем запасенной в синглетном кислороде О₂( а ¹∆) энергии [2]. Для повышения коэффициента усиления необходимо увеличивать концентрации как атомов йода, так и молекул О₂( а ¹∆). Обнаружено [3], что скорость деактивации О₂( а ¹∆) на выходе электроразрядного генератора синглетного кислорода (ЭГСК) растет с увеличением концентраций атомов кислорода [О], молекул кислорода [О₂], а также буферного газа [M]. Темп убыли О₂( а ¹∆) на выходе ЭГСК удовлетворительно объясняется феноменологическим трехчастичным механизмом деактивации [3]

О + О₂( а ¹∆) + М → О + О₂+ М.      (1)

В [4-6] также наблюдали аномально высокую скорость деактивации О₂( а ¹∆) в смесях О-О₂-Ar-He-CO₂ в послефотолизной зоне. При этом добавление Ar не сказывалось на скорости деактивации, а добавление He и CO₂ даже уменьшало темп деактивации О₂( а ¹∆) [6], что находится в противоречии с механизмом (1). Темп убыли O₂( a ¹D) в послефотолизной зоне хорошо объясняется химическим процессом [5, 6]

O₂( a ¹D) + O₃( υ ) → 2O₂+ O,         (2)

где колебательно-возбужденная молекула озона O₃( υ ) образуется в процессе трехчастичной рекомбинации [7]

О + О₂+ М → О₃( υ ) + М.          (3)

Здесь υ = υ ₁ + υ ₂ + υ ₃ – суммарное число квантов на деформационной υ ₂ =701 см^-1 , симметричной υ ₁ =1103 см^-1 и антисимметричной υ ₃ =1042 см^-1 валентных модах молекулы озона [7]. В ряде работ [7-10] также отмечается, что О₃( υ ) эффективно реагирует с O₂( a ¹D). Несмотря на это, процесс (2) ранее не привлекался для объяснения высокого темпа убыли O₂( a ¹ Δ ) на выходе ЭГСК. Целью данной работы является определение влияния процесса (2) на динамику O₂( a ¹ Δ ) в ЭКИЛ.

РЕЗУЛЬТАТЫ И АНАЛИЗ

Кинетическая схема процессов с участием колебательно-возбужденного озона приведена в [6]. Отсутствие измеренных значений вероятностей возбуждения колебательных мод молекулы О₃ в процессе (3) и констант скоростей процесса (2) для конкретных наборов значений υ ₁ , υ ₂ и υ ₃ осложняет моделирование колебательной кинетики озона. В [5] показано, что упрощенная модель колебательной кинетики озона с объединенной модой υ , адекватно описывает экспериментальные результаты, полученные в [4-6]. В процессе (3) образуется молекула озона с υ ≥2 [5, 7]. В столкновениях с частицами среды колебательные кванты перераспределяются между тремя модами

O₃( υ ₁, υ ₂, υ ₃) + M ↔ O₃( υ ₁+1, υ ₂, υ ₃-1) + M

O₃( υ ₁, υ ₂, υ ₃) + M ↔ O₃( υ ₁, υ ₂+1, υ ₃-1) + M.

O₃( υ ₁, υ ₂, υ ₃) + M ↔ O₃( υ ₁-1, υ ₂+1, υ ₃) + M

O₃( υ ) деактивируется в VT процессе [7]

О₃( υ ) + М → О₃( υ -1) + М,          (4)

или удаляется в химических реакциях (2) и

O₃( υ ) + О → O₂ + O₂.            (5)

Скорости реакций (2) и (5) с υ <2 медленные и не оказывают существенного влияния на кинети-

Известия Самарского научного центра Российской академии наук, т.17, №2, 2015

ку O₃( u ) [5]. Для и >  2 в [5] приводятся следующие значения констант скоростей реакций: к ₂ = 4,1 х 10¹¹ см ³ с ^-1 и к 5 = 1,2 ^х 10¹¹ см ³ с ^-1.

Квазистационарная концентрация O₃( u >  2) может быть найдена из баланса его образования в процессе (3) и убыли в процессах (2), (4) и (5):

1 k з^М [О][О 2 ][М]

М

Рз Ф >  2)] =

k 2 [O 2 ( a )] + 1 k 4^M [M] + k ₅[O] ^M                   . (6)

Покажем, что процесс (2) обеспечивает такие же скорости убыли О2(а1∆) как и процесс (1) для условий экспериментов работы [3], где впервые был предложен трехчастичный процесс деактивации. Для этого рассмотрим отношение скоростей этих процессов с учетом (6):

Q = k 2 [O 3 ( u> 2)][O 2 ( a )] ^2/1 1 k ,^M [O][O 2 ( a )][M]

M k 2[O2]1 k 3M[M] M

1 k M I k 2 [O 2 ( a )] + 1 k M [M] + к ₅[О] M V             M

Для условий экспериментов [3]: Ar:O₂=99:1, давление смеси 100 Торр, концентрация молекул синглетного кислорода [O₂( а )]=1,5 ^х 10¹⁵ см³, [O]=2 ^х 10¹⁵ см³, температура смеси T =300 K при к 1A =0,62 х 10^-32 см⁶ с^-1 [3], к 1 ^O2=1 х 10^-32 см⁶ с^-1 [3], к ₃^O2=6 х 10^-34 см⁶ с^-1 [3], к ₃^Ar=0,62 х к 3 ⁰² [3], к 4 ^O2=3 х 10 —14 см³с^-1 [7], к 4 ^Ar=5,9 ^х 10^-15 см³ с^-1 [7] отношение Q _2/1 близко к единице. Следовательно, процесс (2) обеспечивает темпы убыли О₂(а¹∆) на выходе ЭГСК.

Скорость процесса (2) с учетом (6) может быть представлена в виде:

k 2 [O 2 ( a )] 1 k 3^M [O][O 2 ][M]

R = k ₂ [O₃ ( u >  2)][O ₂ ( a )] =----------------------

• ^{2     2L л Л J} k ₂[O₂( a )] + 1 k ₄ ^M [M] + k ₅[O].

M

Для типичных условий в послеразрядной зоне ЭГСК [1]: [He]= 9*10¹⁷ см³, [0₂]= 2,5 х 10¹⁷ см³, [0]=5 х 10¹⁵ см³, [O₂( а )]=3*10¹⁶ см³, T =550 K слагаемые в знаменателе удовлетворяют условию k 2 [O 2 ( a )] >>  1 k ₄^M[M] + k ₅[O] . В этом случае M

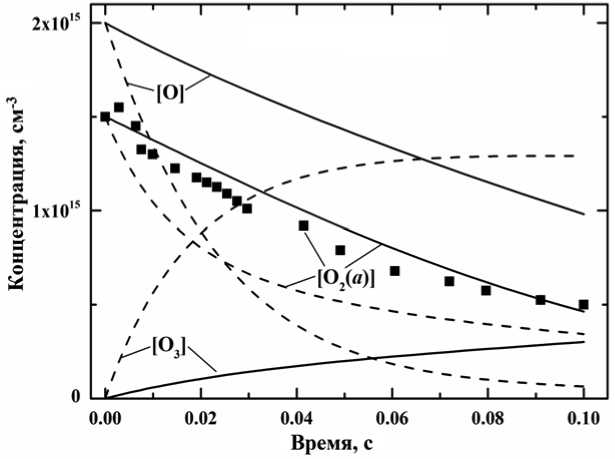
Рис. 1. Временные профили концентраций O, O₂( а 1 Д ) и O 3 в послеразрядной зоне

R 2 « 1 k 3^M [O][O₂][M] и скорость процесса M

• ( 2) лимитируется скоростью образования O₃( υ ) в процессе трехчастичной рекомбинации (3). Это явилось причиной, почему в [3] склонились в пользу трехчастичной деактивации O₂( a ¹ Δ ).

На рис. 1 представлены временные профили концентраций O, O₂( a ¹ Δ ) и O₃ на выходе несамостоятельного разряда для условий эксперимента из [3]: состав газовой смеси Ar:O₂ = 99:1, общее давление P = 100 Торр. Символами обозначены экспериментальные значения концентрации O₂( a ¹ Δ ) из [3]. Сплошными линиями на рисунке показаны расчетные значения концентраций согласно двухчастичному (процесс (2)), а пунктирными – трехчастичному (процесс (1)) механизму деактивации синглетного кислорода.

Из рис. 1 очевидно, что предложенная кинетическая модель двухчастичной деактивации синглетного кислорода обеспечивает лучшее согласование с экспериментально полученными значениями концентрации O₂( a ¹ Δ ), чем трехчастичная. Более того, предложенная модель предсказывает более низкие скорости удаления атомарного кислорода и наработки O₃ вследствие регенерации атомов O в процессе (2). В результате согласно двухчастичному механизму деактивации O₂( a ¹ Δ ) концентрация атомов кислорода падает всего в два раза за 0,1 с , в то же время как в трехчастичной кинетической модели она снижается практически до нуля за такой же промежуток времени.

Реакция (2) может вносить заметный вклад в скорость убыли О₂( а ¹∆) также в разрядной зоне ЭГСК. Рассмотрим отношение скорости данной реакции к скорости самого быстрого процесса в разрядной зоне - деактивации О₂( а ¹∆) электронным ударом

О₂( а ¹ А) + е ^ О₂ + е, (7) константа скорости которой к 7 = 1,02 х 10 -9 см ³ с ^-1[11].

Отношение скоростей процессов (2) и (7) определяется по формуле:

Q 2/7 = k JO,_№ 2>][O _; ( a )] =             ^k .- tO«Q .« Ml

k [e '°/ a >1       k j,/ k ₇[O _₍ a >] , y k ^M[M] + k , [O]1 .

V             M

Для экспериментальных условий [12] отношение скоростей процессов (2) и (7) составляет Q 2/7 « 0,2, в случае когда атомы О не удалялись из системы. В экспериментах с уменьшенной концентрации атомов О за счет добавления NO и покрытия стенок камеры окисью ртути отношение намного меньше Q 2/7 « 0,03. Следовательно, процесс (2) дает заметный вклад в скорость убыли O₂( a ¹ Δ ) также в разрядной зоне ЭГСК в случаях когда имеется избыток атомов О. В [12] за счет удаления избытка атомов О получена рекордная плотность О₂( а ¹∆) в ЭГСК.

ЗАКЛЮЧЕНИЕ

Таким образом, процесс (2) предсказывает наблюдаемые скорости деактивации O₂( a ¹ Δ ) как в послеразрядной [3], так и в послефотолизной [5] зонах. Процессы (2)-(5) также необходимо включать в кинетическую схему процессов разрядной зоны ЭГСК. В ряде работ [4-9] приведены экспериментальные факты в пользу процесса (2), тогда как процесс (1) феноменологический и он не объясняет темпы убыли O₂( a ¹ Δ ) в послефото-лизной зоне [4, 5]. Скорость деактивации O₂( a ¹ Δ ) может быть уменьшена удалением избытка атомов O, например, добавлением в смесь NO [1] или покрытием стенок камеры окисью ртути [12], а также добавлением в смесь на выходе ЭГСК тушителей O₃( υ ), таких как СО₂, SF₆, SiF₄ и т.д.

Работы в СГАУ поддержаны Минобрнауки РФ в рамках программы повышения конкурентоспособности СГАУ на 2013-2020 гг. и Государственного задания вузам и научным организациям в сфере научной деятельности, (гос. задание № 3.161.2014/K), а в СФ ФИАН поддержаны РФФИ (грант № 14-05-97013).