Кинетическая теория образования пакетного мартенсита

2 а / у . ] у у \ 2 7 р/6 ‘

С другой стороны, N6/n = V„/V6, поэтому k=l.J_.(8)

⁷Р ⁷¹ кб

По аналогии с выражением (4), долю превращения ХО во всем у-зерне, а значит, и в образце

(Для нахождения численного коэффициента в (14)

нужно учесть, что

Je ¹ dx = r 1

О              X

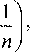
где Г(а)= jf Xxa1dx - гамма-функция, о а Г(4/3)~0,8930 [12].) И в этом случае также возникает связь скоростей зарождения:

L - 03860                         ₍₁₆₎

4 V_6in

С учетом (8) и (16) выражение для общей сте

можно определить, вычислив интеграл по всем

моментам зарождения пакетов т:

пени превращения при малых временах примет вид

/(/>1-ехр(-0.3183^^^ V2),     (17а)

если в структуре пакета блоков нет, и

/(z)«l-exp(-0,04096-(7pHp)3 -Z3),     (176)

если они есть. При больших же временах

/(О ~ 1 - ехр(-/6К/) = 1 - ехр(-0,6366 • 7рЕ • z) (18а)

Если подставить /, из выражения (5), то это выражение преобразуется к виду /=1-ехр -1„У„ <- ^П ^^1 . j exp(-x):t’'^,7t =

=1-ехр

КУ, где п = -^-

7 У р р

"^•(г(ц,цехр(^^^        , (Ю)

= —, переменная интегрирования л

неполная гамма-функция [12]. При малых долях превращения можно воспользоваться для /п выражением (6); тогда интегрирование упрощается:

(И)

если теперь разложить интеграл вероятности в ряд [13, формула 590]:

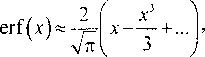
И

/(z)«l-exp(-/nEnz) = l-exp(-0,3860 //pz) (186) соответственно. Иначе говоря, наличие двух- или трехступенчатой иерархии структуры мартенсита (рейка—>пакет или рейка—>блок->пакет) должно приводить к тому, что будет наблюдаться кажущийся переход кинетики превращения от уравнения Аврами

/(z) = l-exp(-^") (19) с н=2 или и=3 к уравнению Аврами с и=1. На рис. 1 показаны функции (5) и (10) в двойных логарифмических осях, которые обычно используются для определения коэффициентов уравнения Аврами (поскольку, как следует из (19), ln(-ln(l- /)) = HlnZ + ln^, то наклон такого графика определяет величину и). Видно, что прямые с наклоном, соответствующим «=2 (и=3) и и—1 действительно являются асимптотами.

Фактически переход от н=2 (и=3) к и=1 связан с тем, что на ранних стадиях превращения идет зарождение пакетов и блоков с постоянной скоростью и их «рост» по закону 1 - exp(-7Ez), а при больших временах время роста каждого отдельного пакета (блока) становится малым по сравнению с общим временем превращения, пакеты образуются как бы «мгновенно», и кинетика определяется только их зарождением.

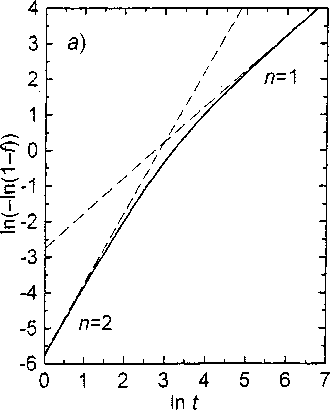
Рис. 1. Функции (5) (а) и (10) (б). Величина произведения /РУР принята равной 0,1

До сих пор при анализе мы полагали, что превращение аустенита в мартенсит проходит до конца: значения выражений (2), (5) и (10) стремятся к единице при / -> ос. В то же время хорошо известно, что мартенситное превращение практически всегда останавливается прежде полного исчерпания исходной фазы.

Наиболее известная попытка построить теорию изотермического развития мартенситной реакции, учитывающую этот факт, была предпринята Пати и Коэном [14]. Они основывались на концепции существования подготовленных зародышей, и полагали, что по мере развития превращения идут два конкурирующих процесса: автокаталитическое образование новых зародышей и поглощение зародышей образующимся мартенситом.

Однако в отечественной научной и учебной литературе в основном принят несколько иной взгляд на причину остановки мартенситного превращения в изотермических условиях: она связывается с изменением состояния исходной фазы в ходе превращения [15, 16]. Накопление дефектов в аустените увеличивает силу сопротивления движению межфазной границы, то есть уменьшает суммарный термодинамический стимул превращения. Когда он становится равным нулю, превращение останавливается, и его дальнейшее развитие оказывается возможным только при понижении температуры.

По Э.И. Эстрину [17], постоянное накопление искажений кристаллической решетки исходной и образующейся фаз должно приводить к непрерывному увеличению удельной (или молярной) энергии искажений. Поэтому полное изменение свободной энергии при у—эос превращении в расчете на моль образующейся сс-фазы можно записать по Эстрину в следующем виде:

-ДО = EG-E (А, (20)

ПОЛИ ИСК W / 7 х z где ДО - разность химических свободных энергий у- и a-фаз. Превращение может проходить, если -ДСПОЛН<0, то есть ДС>Еск; величину Еиск(/) иногда обозначают как ДО, - термодинамический стимул превращения.

Считая ДО, функцией / ее можно разложить в ряд: ДС5(/) = ДС° + Х/+..., гДе AG” - термодинамический стимул начала превращения. Однако энергия искажений, вносимая ос-фазой, накапливается в у-фазе, количество которой равно (1-/). Поэтому в качестве параметра, по которому проводится разложение в ряд, лучше взять отношение f                  df или, точнее, J—=           поскольку накопление искажений происходит непрерывно. Тогда Еиск=ДС5(/) = Д^°-^1п(1-/)+..., где

5AG, _и

5(-1п(1-/))/=0

AGna,„«AG-AG°+Xln(l-/).(21)

В начале превращения / = 0, поэтому положение мартенситной точки Т₅ определяется условием

AG(Tj = AG”.(22)

Но если аустенит переохлажден ниже T_s, то образуется такое предельное для данной температуры количество мартенсита f_m, чтобы

ДО(Г)-ДО>-Х1п(1-Л).(23)

С учетом (21) и (23) изменение свободной энергии системы в процессе превращения можно записать в виде:

ДСП =Х1п--^.(24)

ПОЛЯj

Это - известное уравнение Койстинена-Марбургера [18], выполняющееся для многих сплавов в широкой области температур. Последнее обстоятельство свидетельствует в пользу того, что выражение (21) справедливо не только для малых, но и для широкой области значений/

Выше было показано, что кинетика формирования пакетного мартенсита подчиняется уравнению типа Аврами:

/ = 1-ехр(-Л₀П'')> (26) где к₀ - коэффициент, зависящий от объема кристаллов мартенсита или их групп. Чтобы рассмотреть кинетику изотермического превращения, это уравнение нужно продифференцировать по времени:

^^-^пк_й1"Г\ (27)

а затем вновь проинтегрировать, но уже с учетом зависимости скорости зарождения / от накопленной доли превращения.

Наиболее распространенная теория зарождения мартенсита Кауфмана-Коэна [19, 20] описывает скорость зарождения соотношением

Z = 6expf-3!-^^^ (28) Ч RT J где b, Won а- константы. Однако в работе [21] Бор-генстам и Хиллерт предложили иное выражение:

7 = Z)-^AG™™ -expf—— \ (29) RT ( RT )

которое позволило им с единых позиций описать процесс образования изотермического мартенсита как в «классических» сплавах Fe-Ni-Mn, так и в сплавах Fe-C и Fe-Ni. Сходные идеи развиваются и Э.И. Эстриным [22]. Если воспользоваться соот

ношениями (29) и (24), то дифференциальное

уравнение (27) можно переписать в виде

dz ,

--= пк, z" (

t"^dt,

где

для

где

z = ln

и*1

Z,

. После интегрирования

^Z0 j J 2

1-и

zn=ln

получим

1      , , AG-AG" (

——, а Л = Ь ---ехр -

° RT

скорость зарождения в момент /=0. Из этого выражения следует, что при / = 0 доля превращения / = 0, при t->co она стремится к f_m и, наконец, в

случае /„ -*• 1, если раскрыть неопределенность, левая часть уравнения переходит в -1п(1-/), как и должно быть для превращений, полностью завершающихся в изотермических условиях.

Если и = 1, то решение (30) имеет иной вид:

1п(1-А) (32)

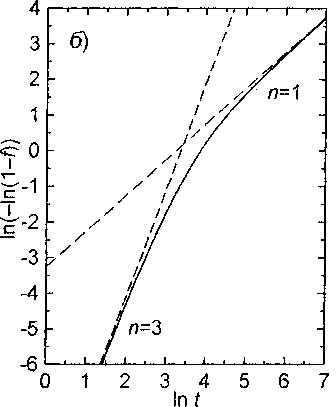
Графики зависимости /(0 согласно (31) и (32) в двойных логарифмических координатах представлены на рис. 2. Отметим, что, в отличие от рис. 1, по оси ординат здесь отложена величина 1п(-Д 1л(1-///„,)), чтобы учесть незавершенность фазового превращения. Видно, что уменьшение термодинамического стимула в ходе превращения приводит к резкому уменьшению наклона графиков (то есть «мгновенного» значения показателя и в уравнении Аврами) - за исключением случая и = 1. Как было показано выше, процесс формирования пакетного мартенсита должен

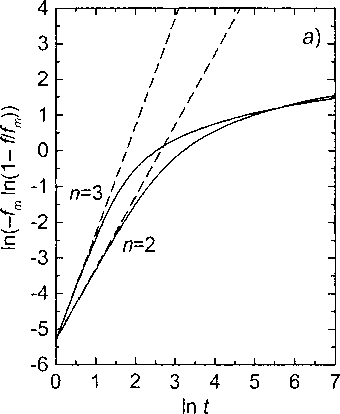
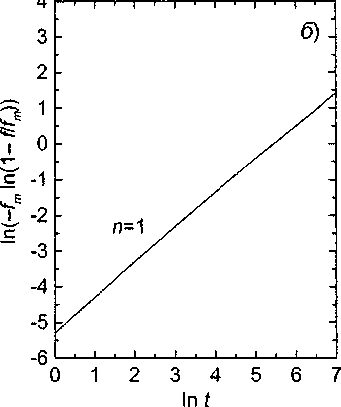
Рис. 2. Функции (31) (а; при различных значениях п) и (32) (6).

Величина произведения kj^ принята равной 0,005; /„ =0,5

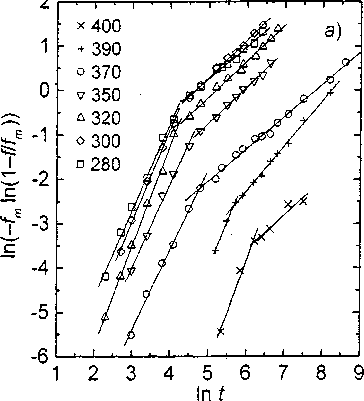
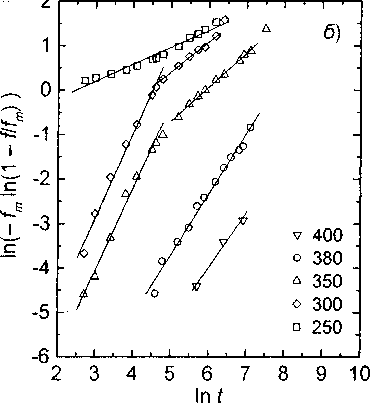
Рис. 3. Экспериментальные кинетические кривые образования мартенсита в сплаве Fe-15%Ni в двойных логарифмических координатах: а — по [23], 6 — по [24]. Время выражено в секундах; температуры превращения в °C указаны у графиков

описываться уравнением Аврами (19) при н = 3 или и = 2 на ранних стадиях превращения и /1 = 1 на поздних. Рис. 2 показывает, что этот вывод сохраняет свою справедливость и при уменьшения скорости зарождения под влиянием образовавшегося мартенсита.

Названные особенности кинетики действительно наблюдаются в ряде сплавов при изотермическом образовании мартенсита. На рис. 3 приведены кинетические кривые образования мартенсита в сплавах Fe- 15 %Ni, перестроенные в двойных логарифмических координатах. На большинстве их отчетливо видно изменение наклона от и = 1,8...2,4 на начальных стадиях превращения до и = 0,7... 1,0 на поздних стадиях.

Работа поддержана грантом Президента Российской Федерации № МК 3549.2007.8 и грантом поддержки ведущих научных школ № НШ-5965.2006.3.