Кинетическая, термофлуктуационная природа разрушения поверхностей трения твердых тел при изнашивании

В середине прошлого столетия получила развитие кинетическая концепция прочности основанная на новых представлениях о термофлуктуационной природе (механизме) разрушения твердых тел, основоположником которой является академик С.Н. Журков с сотрудниками [1, 2]. В соответствии с представлениями температурно-временн ό й концепции прочности долговечность образца под нагрузкой при испытаниях на разрыв определится по следующей экспериментальной зависимости:

t = T ₀exp[(U₀ - yc )/kT], (1) откуда разрывное напряжение

G p = (1/ Y ) (U o - kT ln(t/ T 0 )), (2) а максимальное разрывное напряжение при температуре Т= 0 ^o K

• -:^.; = Uo/Y, (3)

где t – время до разрушения (долговечность) образца под нагрузкой, с.; т ₀=(10^-12...10^-1 3 ) с. -период колебаний атомов в твердом теле; U₀ - энергия межатомной связи, Дж; ст - напряжение, Н/м²; T – термодинамическая температура, ^o K ; k=1.38·10^-23 Дж/^o K – постоянная Больцмана; y — параметр (подгоночный), имеющий размерность объема, м 3 ; (U₀ - yct )=AU - энергия активации разрушения; ст р - разрывное напряжение, Н/м²; – максимальное разрывное напряжение, Н/м².

АКТИВАЦИОННЫЕ ПАРАМЕТРЫ РАЗРУШЕНИЯ

Экспериментальные зависимости (1,2,3) дали возможность исследователям [1.2] оценить численные значения и физический смысл активационных параметров разрушения y , U₀, т ₀ при температурно-временных испытаниях на одноосное растяжение образцов.

Численные значения и физический смысл коэффициента y определены путем вычисления его в модели распада нагруженной атомной ангармонической цепочки, находящейся в тепловом движении [1]:

/ = V/ vJ- X, (4) откуда следует, что y рассматривается как мера локальной перегрузки

X=S/^CT=^CT n / ^CT _p= ZJ. 7 , ⁽⁵⁾ где x - коэффициент локальной перегрузки в месте разрыва созданный концентратором напряжения; S и ст - соответственно, локальное и среднее напряжения; ст _п=Ее₄ - предельная (теоретическая) прочность; Е – модуль Юнга, Н/м²;

– относительное удлинение, при котором межатомная связь теряет устойчивость и разрывается; С – атомная (молярная) теплоемкость, Дж/^o K ( для одноатомных кристаллов С«3к) [1]; а - коэффициент термического линейного расширения, К^-1.

Далее комбинируя (3), (4) и (5), получим:

• = - = U 0 / Y =Ц >^ /(^С Х ); (6)

Х^ = ап^ Ег/, Х=—.

где

U_o = Е,(с/а) [1].             (7)

Таким образом, полученные в [1,2] выражения для параметра γ (4) и энергии механического разрушения (связи атомов в твердом теле) U₀ (7) позволили установить связь прочности σ _р с механо-физическими константами твердого тела: модулем упругости Е, коэффициентом термического линейного расширения α и атомной (молярной) теплоемкостью С. Закономерности (1,2,3) и оцененные значения активационных параметров U₀, τ ₀ и γ позволили интерпретировать механизм разрушения твердых тел с кинетической позиции как термофлуктуационный процесс распада межатомных связей, накопления разорванных межатомных связей, субмикроскопических трещин и генерации зародышевых микротрещин [1].

КИНЕТИКА СОСТОЯНИЯ МАТЕРИАЛОВ ПОВЕРХНОСТЕЙ ПАР ТРЕНИЯ

ПРИ ИЗНАШИВАНИИ

Подтверждением приведенной выше интерпретации кинетической концепции разрушения явились комплексные систематические исследования автора [3,4,5,6,7,8,9] кинетики накопления повреждений структуры и разрушения материалов контактирующих пар при изнашивании в условиях вибрационного трения (фреттинга) в малоподвижных и номинально неподвижных соединениях. Оборудование и средства технического оснащения при проведении исследований описаны в работах [3,6,7,9]. Оценивалась кинетика изнашивания и состояния структуры материалов поверхностей и приповерхностных слоев образцов из титановых сплавов ВТ9, ВТ3-1, бронзы БРАЖМц10-3-1,5 при фретинге образцов титановых сплавов в одноименных парах и в парах с образцами из бронзы и жаропрочного сплава ЖС6К. Установлено, что независимо от природы материалов, условий испытаний и режимов нагружения временны́е зависимости линейного износа имеют ступенчатый, а характеристики изменения состояния материалов – периодический характер. На примере изнашивания сплава ВТ9 (рис.1а) при фретинге в одноименной паре без смазки при амплитуде осцилляции А=0,015 мм, частоте f=310Гц, статической нагрузке q_ст = 7МПа, динамической нагрузке q_дин= 3МПа и температуре Т=293 ^o K можно выделить три характерных стадии износа: П – приработки, I – умеренного износа (латентный период накопления повреждений), II – интенсивного износа (разрущения). Стадии умернного I и интенсивного II износа соответствуют различным структурным состояниям (рис. 1б) кристалической решётки.

Один цикл физического уширения β (интегральной характеристики микроискажений

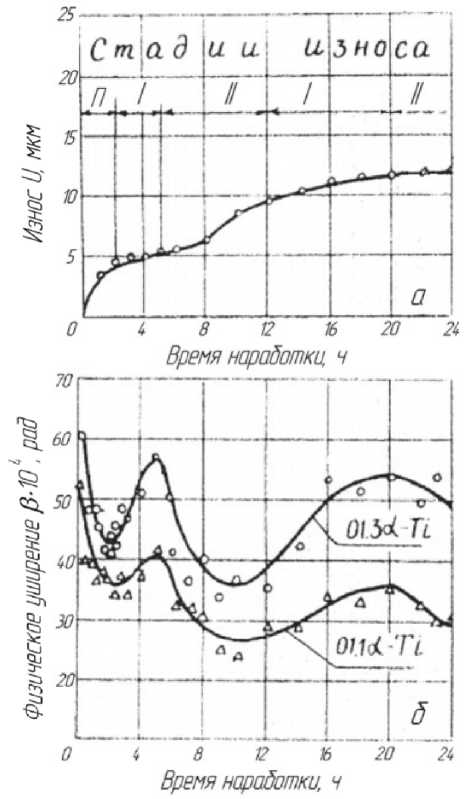
Рис. 1. Кинетика износа (а) и физического уширения рентгеновских интерференционных линий (б) сплава ВТ9

∆d/d кристаллической решетки материала, дробления блоков мозаик D и изменения плотности дислокаций ρ ) рентгеновских линий 01.1 и 01.3 α -Ti, полученных методом дифракции на дифрактометре УРС-50ИМ в медном Cu-K _α излучении, представляет собой последовательные стадии упрочнения, разупрочнения и разрушения поверхностного слоя, обусловленные развитием микроискажений решетки, дроблением блоков мозаик, увеличением плотности дислокаций, образованием и слиянием субмикро - и - микротрещин и отделением частиц разрушенного материала.

Из совместного анализа кривых износа и физического уширения рентгеновских линий (рис. 1 а,б) следует, что на стадии приработки П происходит интенсивное нарастание износа и разупрочнения поверхностного слоя в связи с отделением диспергированных поверхностных структур, упрочненных при предварительной механической обработке, и обнажение нижележащих неупрочненных слоев материала. Шири- на рентгеновской линии 01.3α – Ti уменьшается при этом с 60·10-4 до 41·10-4 рад.

На стадии I умеренного износа физическое уширение резко возрастает, поверхности упрочняются, а износ стабилизируется. На этой стадии происходит накопление дефектов тонкой структуры (фрагментация блоков, рост микроискажений и плотности дислокаций) на поверхности и в зонах влияния по глубине [7, c. 353,354].

На стадии II интенсивного износа наблюдается разрушение, отделение частиц износа и связанное с этими процессами разупрочнение поверхностей, ширина ренгеновских линий вновь уменьшается.

Кинетическая картина накопления повреждений кристаллической структуры и изнашивания сплавов ВТ3-1, ВТ9 в паре со сплавом ЖС6К и бронзой БРАЖМц10-3-1,5, бронзы БРАЖМц10-30-1,5 в паре со сплавом ВТ9 аналогична описанной на примере сплава ВТ9 (рис.1). То есть изменение условий контактирования, материалов контактных пар, параметров механических воздействий, рабочих сред приводит лишь к изменению уровней выходных параметров: амплитуды и периода циклов упрочнение – разрушение – разупрочнение и, следовательно, интенсивности износа рабочих поверхностей трения. Поверхностные слои разрушаются вследствие насыщения кристаллической структуры дефектами, упрочнения, развития хрупкости, потери сплошности и периодической разрядки напряженного состояния на поверхностях и в глубинных уровнях деформируемых объемов [7].

Каждой стадии цикла «упрочнение – разрушение – разупрочнение» соответствует вполне определенный уровень и циклический временн ό й характер изменений комплекса элементарных процессов [7, c 353] на поверхностях трения: износа, физического уширения рентгеновских дифракционных линий β , микротвердости H_М, шероховатости R_Z, относительной опорной площади t_p, демпфирования (логарифмического декремента колебаний) δ , жесткости стыка К, коэффициента трения ц, фазовых а^Р превращений V _β , указывающих на наличие в локальных объемах деформации термических флуктуаций энергии.

Результаты рентгеноструктурного изучения кинетики дефектов тонкой кристаллической структуры сплава ВТ9 на стадиях упрочнения – разрушения в различных глубинных уровнях от поверхности трения при фреттинге в одноименной паре без смазки приведены в работе [7, c. 354, рис. 2]. Использовались рентгеновские излучения с различной проникающей способностью от антикатодов рентгеновских трубок Cr, Fe, Co, Cu, что позволило исследовать послойно состояние дефектной структуры дефор- мированного поверхностного слоя без его разрушения на глубину до 15 мкм. Фиксировалась кинетика изменений микроискажений ∆d/d кристаллической решетки, блоков мозаик D, рентгенографической плотности дислокаций ρ в результате совместной деформации в убывающем градиентном поле внешних эквивалентных напряжений σэкв на контакте и термофлуктуационных напряжений. Общая картина изменения состояния тонкой кристаллической структуры в слоях по глубине при различных уровнях напряжений и деформации показывает, что предварительно упрочненные слои, в результате роста микроискажений, генерации субмикро – и – микротрещин и фрагментации структуры на блоки, в результате которой плотность дислокаций достигает пределов насыщения для данного уровня напряжений, разупрочняются вновь, вследствие разрядки напряженного состояния, снижения прочности, развития хрупкости, нарушения сплошности и разрушения слоя на отдельные элементы дефектной структуры. Наиболее интенсивно описанные процессы протекают в слоях глубиной до 15 мкм, менее интенсивно в глубинных слоях, где оЭкв~0 и сохраняется исходная (технологическая) дефектная структура.

Таким образом, в различных структурных уровнях по глубине от поверхности и на поверхности трения протекают интенсивные структурные и атомно-молекулярные перегруппировки: генерирование, взаимодействие и размножение дефектов связанное с термофлуктуационным разрушением межатомных связей в поле градиентно убывающих напряжений от внешних сил трения.

ОБЪЕДИНЕННАЯ МОДЕЛЬ ПОВРЕЖДАЕМОСТИ И РАЗРУШЕНИЯ ПОВЕРХНОСТЕЙ ТРЕНИЯ

На основе проведенного исследования кинетики деформационных процессов, накопления повреждений структуры и разрушения на поверхностях трения и в приповерхностных слоях сформулированы основные положения многоуровневой объединенной модели повреждаемости и разрушения, а также расчетной модели изнашивания при трении [3,4,5].

В основу предложенной физической модели повреждаемости и разрушения [4, рис.1] положены следующие основные принципы.

• 1.    Контакт шероховатых поверхностей дискретный. Нарушенные фрикционные связи на вершинах микронеровностей при сдвиге поверхностей на величину элементарного пятна контакта «d» возникают вновь на вершинах новых микронеровностей вступивших в контакт, образуя элементарные площадки, в совокупности составляющие фактическую площадь контакта (ФПК)

• 2.    К ФПК приложено эквивалентное напряжение обусловленное совместным действием нормальных и касательных напряжений на элементарных площадках контакта при относительном сдвиге поверхностей.

• 3.    В глубинном уровне, где внешнее напряжение σ =0 [4, рис.1], возможные термофлуктуационные [1] разрывы единичных межатомных связей на технологических дефектах сразу же восстанавливаются вследствие отсутствия поверхностно – активной среды.

• 4.    По мере продвижения дефектных слоев материала из глубинных уровней к поверхности медленно нарастающее внешнее напряжение способствует разрыву межатомных связей и препятствует их восстановлению, создавая направленность термофлуктуационного разрушения в поле внешних сил. Энергия активации термофлуктуационного разрыва межатомных связей ди = U_Q—ya снижается, а вероятность и скорость разрушения возрастают.

• 5.    Разрыв связей происходит в области локальной перегрузки в виде локального активационного объема V» = ^Z (где V_A атомный объем) в вершине микротрещины, перемещающегося по образцу по мере продвижения фронта трещины. Освобождающаяся при разрыве связей энергия приводит к генерированию фононов определенных частот hv = kT (где h=6.626·10^-34 Дж/Гц – постоянная Планка, v = т₀ – частота флуктуаций атомов при данной температуре Т°К, Гц.), их взаимодействию и распространению [11].

• 6.    На поверхности и в приповерхностных слоях накапливается множество локальных объемов (структурных элементов) с различным уровнем прочности, размеры которых Ч) = v_AXt определяются величиной коэффициентов локальной перегрузки. Разрушение происходит в локальных объемах, где действующие напряжения достигают локального предела

Поверхностные контактные напряжения распространяются в глубинные слои, в соответствии с принципом Сен-Венана [10], создавая градиент убывающих по величине напряжений от внешних сил. Специфика контактного взаимодействия и деформации, обусловленная дискретностью шероховатого контакта и градиентом напряжений, создала условия наблюдаемой выше кинетики накопления повреждений структуры и разрушения на трущихся поверхностях и на различных структурных уровнях зон влияния по глубине. В деформируемых структурных уровнях периодически возникает высокая плотность элементарных дефектов, при взаимодействии которых генерируются и распространяются более сложные дефекты и повреждения, являющиеся локальными концентраторами механических и термических напряжений.

прочности наиболее слабого элемента структуры (хрупкое разрушение) или усредненного предела прочности ^ffp = <Ъ = »JX , где O"g - предел прочности, группы структурных элементов (вязкое разрушение). Разрушение завершается отделением частиц, размеры которых определяются размерами областей микронеоднородностей или элементов деформированной структуры.

АКТИВАЦИОННЫЕ ПАРАМЕТРЫ РАЗРУШЕНИЯ ПОВЕРХНОСТЕЙ ТРЕНИЯ

В твёрдых телах без микроповреждений в момент приложения нагрузки все межатомные связи нагружены равномерно, реализуется механизм одновременного разрыва связей. В этом случае коэффициент перегрузки цепей χ =1, локальный объём разрушения

γ = VA χ = Va = , где ^0 – межатомное расстояние, ^fH. – расстояние между минимумом и максимумом потенциальной энергии при разрыве, 4 – локальный атомно-молекулярный объём [11,12], а время ожидания флуктуации определится из уравне-ния(1), как t = τ0exp[(U0 - у^зм)/kT], разрывное напряжение (2),

σ р= «о / V_A -(kT/ V_A )ln(t/ τ ₀ ), предельная прочность (3),

°?i ^p.max   ^0 / 4i .

В реальных телах с дефектами x > i, γ = vA χ = 4} , где ^ 0 – область локальной перегрузки в вершине микротрещины (трещины) или локальный нано -микрообъём разрушения, в котором ожидается флуктуация кинетической энергии. В этом случае время ожидания флуктуации t = τ0exp[(U0 – 4)°™)/kT], разрывное напряжение

σ р= U_Q / 4> –(kT/ Vo)ln(t/ τ ₀ ), предельная прочность

»„=и0/Vo-

Кумулятивное накопление дефектов

(13) при-

водит к образованию групп структурных элементов с локальным активационным объёмом разрушения 4) с низшим уровнем прочности ^ap = ^ав . Локальный активационный объём ^0 физически и математически (11) связан с временем ожидания флуктуации t в этом объёме, что, как показано ниже, является основополагающим в механизме термофлуктуационного разрушения этого объема и может быть использовано в расчётах скорости изнашивания.

Размерная идентификация расчётных активационных параметров разрушения при изнашивании в условиях фреттинга титанового сплава ВТ9 [6,7] показала следующие пределы их рассеяния:

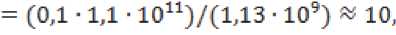
математическое ожидание параметра _Х: МО^ ^ 10/2 ^ 5, то есть рассеяние коэффициента локальной перегрузки происходит в пределах одного порядка величин, что согласуется с данными источника [2]. Далее:

1,38·10-23)/(8,5·10-6)=

=0,0487·10-17 Дж;

• V» = (С/а^ =

  =(3·1,38·10^-23)/( 8,5·10^-6·1,1·10¹¹)=

  =4,4278·10^-29 м³;

4,4278·10-29 м3, при χ=1;

4,4278·10-28 м3, при χ=10.

• ^u max ^{л л}

Данные экспериментального электронографического исследования частиц износа [7] экстрагированных с угольной репликой, характеризующих исходное, не подвергнутое многократному перетиранию, состояние поверхностных структур и отделившихся от образца частиц (блоков мозаик D) показывают, что размеры областей когерентного рассеяния (ОКР) составляют, в основном, порядка (7-15) Å и очень близки к расчётным размерам локальных активационных объёмов структуры с дефектами:

=

(3,43·10-28… 3,375·10-27) м3.

ТЕРМОФЛУКТУАЦИОННАЯ МОДЕЛЬ РАЗРУШЕНИЯ ПОВЕРХНОСТЕЙ ТРЕНИЯ ПРИ ИЗНАШИВАНИИ

В основу описания большинства современных моделей изнашивания [10,13,14,15] положены выходные (конечные) объёмные макрохарактеристики процесса: например, число отделившихся с сопряжённой поверхности атомов «Z» на единичном пути трения; деформируемый объём « » равный объёму материала взаимно внедрившихся выступов шероховатости поверхностей, разрушаемый за определённое число циклов взаимодействий «n» [10]; объём удаляемого с поверхности трения материала за цикл изнашивания в результате разрушения определённого количества «λ» межатомных связей этого объёма с основой [13,14]; деформируемый объём равный объёму взаимно внедрившихся субмикрошероховатостей [15].

Очевидно, что такие модели не могут привести к желаемым положительным расчётным результатам в силу неопределённости размеров и границ вовлечённых в контактную деформацию объёмов материалов и отсутствия конечных условий по времени или количеству циклов взаимодействий до их разрушения. Использование в расчётной модели изнашивания [5] локального активационного объёма разрушения «V0» структурного элемента или группы структурных элементов, сформированного в процессе деформации по естественному термофлуктуационному механизму и имеющего прямую математическую связь (11) с временем ожидания флуктуации t , исключает перечисленные выше неопределённости.

Примем, что в установившемся режиме трения и изнашивания разрушение активационного объёма V0, в каком бы уровне по глубине поверхностного слоя он ни находился, в конечном итоге будет эквивалентно отделению с номинальной площади поверхности трения слоя материала толщиной

,

где .-;. - номинальная площадь поверхности трения, м2;     активационный объём, м3;

– толщина отделяемого слоя материала, м. Скорость износа, с учётом (11) и (14),

=      (15)

= "V Ч!и: Т„■ =xp«u„- ';.7„,)1И1), где   – скорость линейного износа, м/с; – гео метрический фактор (число опорных точек или число условий связи относительного движения поверхностей в контактах: плоскость

–

пло-

скость, =3; по линии, =2; в точке, =1). Учитывая, что

^ = v = kT/h;

с учётом (4) и (5),

=;

U0, с учётом (3), и0 = <С ::, получим расчётную модель скорости изнашивания поверхностей трения в широком температурном диапазоне в виде:

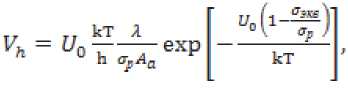
или с учётом выражения (16) для ,

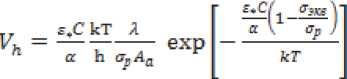
Уравнение (17) удобно применять при использовании значений полученных экспериментально, уравнение (18) – при использовании расчётных значений.

Эквивалентное напряжение при одновременном действии нормальных и тангенциальных напряжений на поверхностях трения опре- делится из выражения:

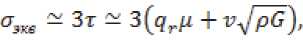
где °™ – эквивалентное напряжение, Н/м²; т – касательное напряжение на поверхности трения, Н/м²; 9 г – фактическое давление в контакте, Н/м²; {.t – коэффициент трения; V – скорость скольжения, м/c; р – плотность, кг/м³; G ≈ 0,38E – модуль сдвига, Н/м²; V = 2π Аf, м/c – скорость скольжения при возвратно-поступательном и вибрационном трени; А – амплитуда, м; f – частота осцилляций, Гц.

При практических расчетах в условиях малых и средних нагрузок на контакт пластическая деформация возникает на выступах микронеровностей, материал «течет» в зазор, а среднее фактическое давление в контакте достигает 9 г = (1,1÷1,3)Стр . При высоких нагрузках внедрение микронеровностей увеличивается, пластическая деформация распространяется по всему контакту, фактическое давление растёт до Чг ≈ 3 Cjp [10] , а эквивалентное напряжение достигает или превышает предел прочности °ЭК6 — ^ар , что приводит поверхностный слой в состояние низшей прочности (°р - "в) и к ведущей роли «атермического» механизма разрушения, когда время ожидания термических флуктуаций становится больше времени действия нагрузки. При ^/"р * ¹, энергия активации (15,16,17) ДУ = U_n-V_na = 0, работа внешней силы v v 33(6

to^ становится равной энергии связи атомов в твердом теле tz 0 ,

^0 — 4>°»х*

показатель экспоненты в уравнении (17) ным нулю, а экспоненциальный член

рав-

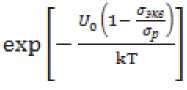
= exp(-0) = 1.

Учитывая (20,21) уравнение (17) перепишется в виде:

„   s.C кт <т_эяв Л ^h a h ap A_a

.

Наряду с атермическим механизмом разрушения при Т >0 ^o K действует термофлуктуационный, что следует из анализа предэкспоненци-ального члена уравнений (17,18), (22), поэтому понятие атермического механизма разрушения при температурах б6льших абсолютного нуля является условным.

Проведена широкая идентификация модели (22) при вибротрении и фреттинге в лабораторных условиях, при стендовых и эксплуатационных испытаниях [3,6,7,9] сплавов ВТ9, ВТ8, ВТ3-1, ОТ4, 20Х13, ЖС6КП, 40ХНМА в различных температурных режимах. Расчётные данные удовлет- ворительно согласуются с экспериментальными. Рассеяние большинства экспериментальных данных вокруг расчётных значений не превышало ±23%, отдельные индивидуальные экспериментальные значения скорости изнашивания варьировали в диапазоне не более ±36%.

ВЫВОДЫ

Предложена кинетическая термофлуктуационная модель изнашивания при трении, прошедшая широкую идентификацию в условиях вибрационного трения и фреттинга. В модели используются механические и физические параметры и константы материалов при полном отсутствии подгоночных и эмпирических коэффициентов. Оценены локальные активационные объёмы разрушения, формируемые в процессе деформации по естественным термофлуктуационным механизмам. Для расчёта скорости изнашивания использована прямая фундаментальная математическая связь формируемых локальных активационных объёмов с временем ожидания флуктуаций кинетической энергии (разрушения). Предложенная модель изнашивания пополнит арсенал расчётных методов оценки износа при трении.