Кинетические закономерности образования перлита из аустенита, подвергнутого деформации

Известны несколько исследований [1-3], в которых отмечено ускорение перлитного распада под влиянием предварительной горячей пластической деформации, проведенной выше или при температуре превращения у-фазы. В качестве возможного объяснения этого эффекта приводились соображения об ускорении диффузии углерода, об измельчении зерна, об ускорении зарождения перлитных колоний в аустените с повышенным содержанием дефектов. Но, по существу, детального исследования кинетических изменений сделано не было. Такой анализ является целью настоящей работы. Он базируется на экспериментальных результатах работы [4], частично дополненных новыми данными тех же авторов.

Кинетика превращения аустенита при постоянной температуре обычно описывается при помощи уравнения Аврами

/ = 1-ехр№"), (1) в котором / представляет объемную долю продуктов превращения в момент времени т, а К и п - коэффициенты [5]. Коэффициент К зависит от скоростей зарождения новой фазы 7 и ее роста со; в простейшем случае, когда эти скорости постоянны, и рост изотропен,

К = (л/З)7ю3; н = 4. (2)

Однако в действительности процессы зарождения и роста в объеме поликристаллического материала протекают неоднородно. Например, границы зерен очень часто выступают в роли мест предпочтительного зарождения новой фазы. Все это должно приводить к зависимости коэффициентов уравнения (1) от среднего поперечника зерен аустенита d. В частности, скорость зарождения I пропорциональна количеству возможных мест зарождения в единице объема; поэтому если зарождение протекает в основном на границах зерен, то должна наблюдаться зависимость I~d"^x и, соответственно, К ~ d~^x ; если преимущественными местами зарождения являются тройные стыки, то К ~ d"² и т.д. [5]. С другой стороны, преимущественное зарождение кристаллов новой фазы на границах и их быстрый рост вдоль границ могут приводить к «исчерпанию» мест зарождения, после которого превращение развивается в основном за счет роста ранее образовавшихся кристаллов; в этом случае будет наблюдаться уменьшение показателя степени и на поздних стадиях превращения [5]. Пример такого поведения наблюдали в сплавах Fe - 9 % Сг, где образование ферритной сетки приводило к уменьшению и от 4 до 1 [6].

В работах [7, 8] И.Тамура с соавторами подтвердили, что кинетика распада аустенита в ряде малолегированных сталей подчиняется уравнению (1), а коэффициент К зависит от размера зерна:

к=^-- <3)

Экспериментально найденные значения X составили 1,76 (при и®4) для перлитного превращения в стали типа 4Х5МФС [7] и 0,65 (при п «4...5) для бейнитного превращения в стали типа ШХ15 [8].

В исследовании [4] приведены результаты изучения кинетики перлитного распада в углеродистой эвтектоидной стали 85 после предварительной пластической деформации аустенита, осуществлявшейся кручением в интервале температур 650...900 °C со степенями деформации £ = 0,11...2,6. Увеличение степени деформации приводило к существенному ускорению образования перлита. Этот эффект может быть обусловлен либо повышением плотности дефектов в аустените вследствие горячей пластической деформации, либо измельчением аустенитного зерна, если в ходе деформации и во время переноса образца из пластометра в ванну, где происходил распад аустенита, успевала пройти рекристаллизация. На возможность того, что аустенит был рекристаллизован до начала распада, указывают такие отмеченные авторами [4] факты, как существенное измельчение зерна при увеличении степени и понижении температуры деформации и отсутствие зависимости межпластиночного расстояния и микротвердости образующейся перлитной структуры от параметров деформации аустенита.

Чтобы определить параметры уравнения (1), мы перестроили приведенные в [4] кинетические кривые распада аустенита при 650 °C в двойных логарифмических координатах 1п(-1п(1-/)) - 1пт, поскольку, как следует из (1),

Ь(-1п(1-/)) = и1пт + 1пХ". (4)

Полученные графики действительно в большинстве случаев оказались линейными (рис. 1), что позволило найти значения коэффициентов и и К (табл. 1). Значения показателя и обычно составляли 2,5...3,5, что в целом согласуется с данными других работ, посвященных кинетике перлитного распада [7, 9, 10].

Приведенные в [4] данные указывают на существенное измельчение зерна аустенита при увеличении степени пластической деформации, поэтому можно ожидать, что коэффициент К будет

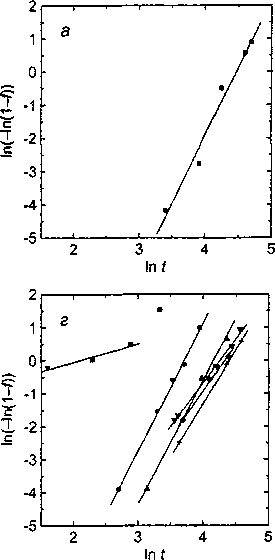
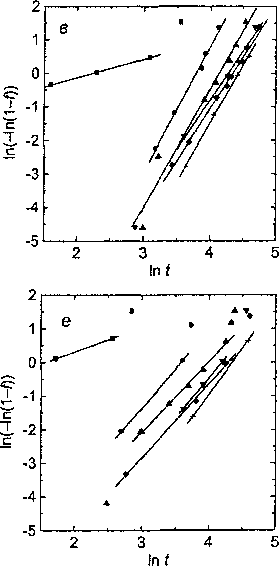
Рис. 1. Кинетические кривые распада аустенита [4], перестроенные в двойном логарифмическом масштабе (время выражено в секундах). Температуры деформации аустенита: ■ - 650 °C; □ - 675 °C; • - 700 °C;

▲ - 750 °C; ▼ - 800 °C; ♦ - 850 °C; + - 900 °C. Степени деформации: а - 0; б - 0,11; е - 0,35; г - 0,70; б -1,3; е - 2,6

Таблица 1

Коэффициенты уравнения (1), найденные по графикам рис. 1

Степень деформации Температура деформации, °C И 1п£ 0 — 4,08 -18,24 650 0,94 -2,62 700 4,00 -15,61 0,11 750 3,70 -15,49 800 3,52 -15,18 850 3,78 -16,59 900 4,09 -17,99 650 0,55 -1,23 700 3,74 -14,18 0,35 750 3,52 -14,57 800 2,94 -12,60 850 3,10 -13,48 900 3,48 -15,42 650 0,54 -1,14 700 3,87 -14,36 0,70 750 3,77 -15,66 800 2,63 -11,19 850 2,79 -12,07 900 3,24 -14,27 650 1,05 -2,32 675 2,32 -7,40 700 3,52 -12,70 1,3 750 2,76 -11,17 800 2,56 -10,82 850 2,44 -10,47 900 2,67 -11,70 650 0,72 -1,14 700 2,33 -8,37 2,6 750 2,10 -8,39 800 2,38 -9,99 850 2,21 -9,50 900 2,75 -11,96 подчиняться зависимости (3). Если прологарифмировать выражение (3), то окажется, что график зависимости I n А? от hit/ должен быть линейным с наклоном, равным -X. Однако, поскольку значения и и К взаимосвязаны, а величины показателя п, как видно из табл. 1, обнаруживают заметный разброс, то правильнее по оси ординат откладывать не

In/С, а — In ^ = Ln А'1-”: тогда и

-]n^ = --lnt/+-lnAL1.               (5)

и пи _                   1 d^Xi"

Величина т063 = —представляет со бой характерное время превращения у-фазы на 63,2 %, как это следует из выражения (1), если его переписать в виде / = 1 - ехр ^-(К'!”тУ ). Соответ ственно -—1пА' = 1пт0И. Графики зависимости п               ■

—InA" от In <7 приведены на рис. 2. Видно, что они п действительно линейны для каждой температуры деформации, однако с понижением этой температуры их наклон уменьшается. Найденные по графикам значения отношения Х/п приведены в табл. 2; в основном они близки к 0,2.

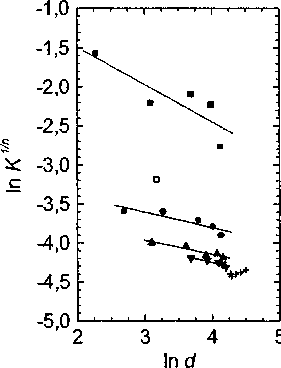
Рис. 2. Зависимость In/C^" от логарифма размера зерна (выраженного в микронах); обозначения температур деформации те же, что и на рис. 1

Таблица 2

Параметры уравнения (5), найденные по рис. 2

Температура деформирования, °C	X п	In/С, п
650	Q,A1%	-0,535
700	0,198	-3,013
750	0,181	-3,421
800	0,198	-3,459
900	-0,281	-5,615

Зависимость характерного времени превращения от размера зерна указывает на участие границ в процессе зарождения. Для варианта превращения с постоянными скоростями роста и объемного зарождения из формул (1) и (2) следует, что

_ i Г з f То.63  _Г/4-| _/(0з!

и не зависит от размера зерна. Но если зарождение перлитной колонии происходит на границе зерна, а скорость зарождения в расчете на единицу площади равна /гр, то скорость образования зародышей (сферической формы) в расчете на единицу объема составит i = i W!Ty _з/л гр 2-(4л/3)(-//2)3 d

то есть появляется теоретическая зависимость характерного времени от размера зерна:

/       V/4

т = ^d ~

10,63 т 3 U .

Запишем в общем виде

То,63=Р^'”>

где р = К, ^1/л, а т = Х[п . Кристиан, основываясь на работах Кана, приводит [5] значения т, которые характерны для различных вариантов зарождения: на границах зерна /и = 1/4 = 0,25, на ребрах т = \/2, на вершинах зерен m = 3/4. Для случая исчерпания мест зарождения т = 1. Результаты обработки экспериментальных зависимостей т = 0,20...0,28 ближе всего к ситуации зарождения на границах зерна. Напомним, что И. Тамура с соавторами [7] получили т = 1,76/4 = 0,44, что примерно соответствует ситуации зарождения на ребрах зерен.

Полученный результат можно рассматривать как свидетельство того, что наблюдаемое ускорение превращения под действием предварительной деформации аустенита в значительной мере обусловлено измельчением зерна в результате рекристаллизации, успевающей протекать в интервале между окончанием пластической деформации и фиксируемым началом превращения.

Отметим, что в ряде случаев деформация при разных температурах с разной степенью обжатия приводила к получению одинакового размера аустенитного зерна. Сравнение кинетических кривых распада аустенита после таких режимов деформации (рис. 3) показывает, что они практически совпадают, за исключением деформации при 650°С, когда превращение начинается еще в ходе деформирования. Иными словами, зависимость кинетики превращения от температуры деформации при одинаковом размере зерна как будто отсутствует. Однако наличие зависимости параметров уравнения (5) от температуры деформации может свидетельствовать о том, что к моменту начала превращения аустенит все же оставался

фиках

In t

In t

частично наклепан, и ускорение превращения частично обусловлено и повышенной плотностью дефектов.

Для температуры деформации 650 °C величина-и = 0,54... 1,05 резко отлична от значений для других температур деформации. При этой температуре наблюдается наибольшее ускорение превращения при всех степенях деформации. Рекристаллизация в у-фазе при малых степенях деформации (И %), по-видимому, отсутствует, поэтому проявляется в полной мере эффект влияния возникающих дислокаций. Деформация ускоряет прежде всего превращение по границам зерна. Переход к и и 1 означает, что колонии перлита развиваются весьма быстро вдоль границ, а затем слой перлита начинает расти к центру зерна. Это и есть одномерный рост при и = 1. Отклонения от и = 1 в меньшую сторону следует рассматривать либо как проявление уменьшающейся со временем скорости роста, либо как результат неточности при измерениях слишком малых длительностей распада.

Рассмотрим далее характер изменения параметра п (рис. 4) в зависимости от степени и температуры предварительного деформирования. Если отвлечься от детального анализа, то при всех температурах увеличение степени деформации приводит к уменьшению величины и от 4 до 2,1...2,8. Теоретически значение и = 4 получается в том случае, когда число возникающих зародышей увеличивается линейно со временем, а объем зародыша возрастает со временем по закону (4л/3)ю³(т-т₃)³, характерному для трехмерного роста с постоянной скоростью о вдоль каждой оси

(здесь т3 - момент зарождения). При этом неважно, происходило ли зарождение в объеме или на границах. Уменьшение величины и с 4 до 3 можно трактовать как быстрое гетерогенное зарождение, приведшее к исчерпанию мест зарождения. Длительность превращения определяется ростом колоний до столкновения. Согласно рис. 4, для температур 800 и 850 °C уменьшение и до 3 происходит после деформации на степень 35 %, когда уже отчетливо проявляется рекристаллизация. Возникающие при рекристаллизации зерна задерживаются частицами неметаллических включений, которые выделяются из у-фазы при температуре деформации. Эти и более крупные нерастворяющие-ся частицы стимулируют зарождение перлита [11], причем наличие концентрационных изменений вокруг частиц ускоряет зарождение.

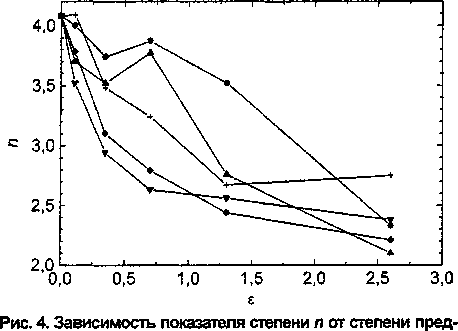
варительной деформации е (по данным табл. 1). Обозначения температур деформации те же, что и на рис. 1

Уменьшение величины и ниже 3 требует особого объяснения. Рост перлитной колонии, очевидно, происходит вдоль сопрягяющихся слоев цементита и феррита. Продольный рост фактически является двумерным. Рост же колонии по направлению нормали к пластинам связан с диффузионным утолщением крайней пластины до толщины, при которой продольный рост имеет максимальную скорость [И]. Затем происходит очередное зарождение пластины другой фазы, ее рост и т.д. Не вполне понятным остается вопрос, почему колония перлита имеет примерно сферическую форму и с помощью какого механизма выравниваются скорости продольного роста и поперечного роста-зарождения.

Переход от значения и = 3 к и = 2 можно объяснить резким ускорением зарождения в поперечном направлении, так что сначала образуется как бы слоистый цилиндр, радиус которого затем линейно возрастает со временем. Значения 2 < и < 3 соответствуют промежуточной ситуации, когда зарождение пластин, то есть «рост в поперечном направлении» до остановки опережает продольный рост.

Причиной изменения показателя и несомненно является пластическая деформация аустенита, которая а) в условиях кручения осуществляется скольжением по плоскостям, параллельным круговому сечению; б) приводит к образованию текстуры, вероятно, типа [111]7 вдоль оси образца, ибо плоскости скольжения стремятся установиться параллельно действующим напряжениям; в) приводит к накоплению дислокаций, полигонизации и сегрегаций углерода на них. Таким образом, в аустените могут возникать и искажения решетки, благоприятствующие образованию новой решетки, и участки с низкой либо высокой концентрацией углерода, необходимые для зарождения а-фазы или цементита. Но если предварительная деформация стимулирует зарождение, то, по нашему мнению, продольный рост пластин после деформации замедляется. Можно указать две причины торможения роста. Одна обусловлена замедлением диффузии углерода в деформированной у-фазе. Коэффициент диффузии углерода играет определяющую роль в процессах роста. Теория [11] дает следующие выражения для скорости роста:

• а)    в приближении объемной диффузии углерода в у-фазе от участков, контактирующих с торцом ферритной пластины, к участкам, контактирующим с цементитной пластиной,

co = prAT2-Z)c; (Ю)

• б)    в приближении граничной диффузии по межфазной границе

ф = ^₂-М³-П^, (И) где D^¹ - коэффициент граничной диффузии, Pi и Р₂ - постоянные коэффициенты, а АТ - переохлаждение относительно A_v

Миграция атомов внедрения по дислокациям происходит быстрее, чем в объеме, из-за пониженной энергии активации [12], но ориентация дислокаций случайна и не обязательно совпадает с нормалью к пластинам феррита и цементита. Кроме того, дислокация не выпускает все атомы углерода. Другая причина торможения обусловлена искривлениями, поворотами участков аустенита при деформации. По закону парности касательных напряжений, при кручении тф2 = т2ф. Касательное напряжение тф- действует вдоль окружности по площадкам с нормалью z, то есть по круговым сечениям цилиндра. Они создают скольжение, о котором шла речь выше. Второе напряжение тгф действует вдоль оси z по площадкам с нормалью ёф. Эти площадки проходят через радиусы и ось г. Сдвиги, обусловленные этими напряжениями, происходят во взаимно перпендикулярных плоскостях, что и вызывает искривления решетки. Решетка цементита находится в ориентационном соответствии с решеткой у-фазы, поэтому искривления и повороты у-решетки передаются пластинам цементита (см. данные электронной микроскопии), что должно вызывать торможение роста.

Эффект деформации, таким образом, двойственен: ускоряется зарождение перлитных колоний и тормозится их рост. Это вызывает изменение кинетических параметров п и т,. но суммарное влияние деформации на перлитный распад (без учета рекристаллизации) выражено слабо.

Работа поддержана грантом правительства Челябинской области для молодых ученых, грантом № 14-04-02 ИТЦ «Аусферр», РФФИ-Урал № 04-03-96140-урал_а, а также грантом поддержки ведущих научных школ НШ-778.2003.3.

Выводы. В работе проанализированы данные о кинетике изотермического перлитного превращения в углеродистой эвтектоидной стали после предварительной горячей деформации аустенита при температурах 900...650 °C. Сделан вывод, что ускорение распада при всех температурах деформации, кроме 650 °C, вызвано в основном измельчением зерна вследствие рекристаллизации аустенита, хотя влияние наклепа аустенита на кинетику превращения также проявляется. Подтверждена зависимость коэффициентов уравнения Аврами от размера зерна d вида К^" ~ d"^" , причем отношение А./и близко к 0,2 и уменьшается при повышении температуры деформирования.