Кинетическое моделирование биомеханических процессов

Предлагаемая работа посвящена кинетическому моделированию некоторых процессов из области биодеструкции лекарственных средств, биодоступности и прочности капсул с биологически активными добавками и лечебными грязями, а также (в качестве теоретического предложения) из области заживляемости мягких тканей человека в послеоперационный период.

Следует отметить, что вопросам кинетики биомеханических процессов посвящено достаточно много работ. Так, в работе [1] рассмотрена кинетика перемещения неправильно расположенных зубов в нормальное положение с применением эластопозиционеров, в работе [2] исследованы предпосылки кинетики процесса сушки мягких желатиновых капсул с гидрофильными наполнителями, а в работе [3] рассмотрены биомеханические аспекты восстановления слуха при отосклерозе.

В качестве первого объекта кинетического моделирования рассмотрен один из аспектов проблемы утилизации лекарственных средств с истекшим сроком годности. Данные лекарственные средства признаются фармацевтическими отходами и подлежат обязательному уничтожению. Рекомендуемые методы их уничтожения не являются экологически безопасными и требуют существенной доработки. Сегодня приоритет по показателям эффективности, безопасности и экономичности признается за биотехнологическими способами утилизации опасных отходов [4].

В качестве второго приложения кинетического моделирования рассмотрено производство капсул с биологически активными добавками и лечебными грязями в оболочке на основе желатина. Для обеспечения биологической доступности и необходимых свойств капсул в процессе формования, шлифовки, упаковки и хранения применяется сушка при повышенной температуре и в естественных условиях. Данная работа посвящена экспериментальному исследованию процесса сушки капсул с гидрофильными наполнителями, а также определению механических характеристик капсульной оболочки с целью оценки стабильности формы и ее биодоступности. Построена кинетическая модель процесса сушки, определены значения скорости сушки для наполнителя, оболочки и капсулы в целом. Отмечено нетрадиционное для сушки нарастание влажности наполнителя капсулы во время активного периода. Исследована распадаемость капсул в биологической среде как один из важнейших показателей биодоступности в зависимости от параметров сушки [5].

Помимо двух тем применения кинетического моделирования, предлагается кинетическая модель заживления мягких тканей человека.

В табл. 1 представлена структура данной работы. Зависимости, отраженные на рисунках в табл. 1, могут быть экспоненциальными, линейными, параболическими. В отличие от химической кинетики, константы реакций зависят от желудочной микрофлоры, активности патогенных бактерий и вирусов, т. е. являются функциями времени.

1.    Биодеструкция как биомеханический процесс

Процесс биодеструкции лекарственных средств - производных фенола (на примере парацетамола) охарактеризован кинетическим уравнением первого порядка. С помощью данного кинетического уравнения получены значения технологических параметров (температуры и угловой скорости вращения мешалки ферментера), обеспечивающие максимальную интенсивность разложения исследуемого вещества [6].

Исследования показали, что введение переменной во времени «константы» скорости реакции позволяет адекватно описывать результаты биодеструкции вышеупомянутой группы лекарственных средств.

Следует отметить, что процесс биодеструкции происходит с участием микроорганизмов, требующих особых условий подготовки (адаптации бактериальных клеток к структурному аналогу исходного субстрата, использования косубстратов, иммобилизации на носителе), и продолжителен во времени. Подача питательных веществ колониям бактерий осуществляется механическим путем при перемешивании культуральной жидкости. Идентификация и количественное определение исходного соединения и продуктов его разложения предполагают использование современных методов анализа (высокоэффективной жидкостной хроматографии, хромато-масс-спектрометрии, спектрофо- тометрии и др.). Подготовка микроорганизмов, проведение процесса биодеструкции и анализ проб определяют «цену» каждой экспериментальной точки.

Таблица 1

Биомеханические процессы

Биодеструкция лекарственных средств (экспериментальнотеоретическое исследование)	Биодоступность    _ Регенерация желатиновых капсул             „ мягких тканей (экспериментально- , (теоретическое жрртд ржтлттррцтдр           1 теоретическое                  х х     исследование) исследование)
Исходный      Вторичный субстракт         продукт 1.    Парацетамол 1. Парааминофенол 2.    Парааминофенол 3.    Бензоат натрия 4.    Дротаверина гидрохлорид (но-шпа)	Гидрофильные   1. Брюшина наполнители    2. Жировая 1.    Лечебные грязи   ткань 2.    Биологические    3. Кожа активные добавки

Особенности		Особенности	Особенности
Зависимость от иммобилизации актинобактерий типа Rhodochrous ИЭГМ 647		Влажность желатиновой оболочки -определяющий фактор механических свойств оболочки и биодоступность содержимого	Различная скорость послеоперационного заживления
Параллельное экспериментальное математическое моделирование	Открытая система
Выход		Выход	Выход
Прогнозирование времени окончания процесса уже по 3 точкам	Определение времени окончания процесса	Прочность оболочки и биодоступность содержимого в зависимости от конечной влажности	Управление временем заживления тканей после операции

Кинетическое моделирование позволяет уменьшить количество необходимых экспериментальных точек и произвести количественную оценку эффективности процессов биодеструкции при варьировании параметров.

В работах по математическому моделированию процессов биодеструкции лекарственных средств были разработаны кинетические уравнения, адекватно отражающие динамику начальных концентраций как исходных субстратов (в частности, парацетамола, парааминофенола), так и первичных продуктов их разложения (например, парааминофенола при биодеградации парацетамола) [5-7].

При биодеструкции в качестве первичного субстрата (парацетамол, парааминофенол) независимо от штамма родококков, участвующих в реакциях, процесс адекватно отражают кинетические уравнения первого порядка типа dr

d t

■ K ( t ) • r ,

где «константы» реакции K ( t ) = a t + b - линейные функции времени деградации; r - концентрация субстрата, а знак «-» уменьшение концентрации при биодеструкции.

Здесь параметр b имеет размерность [1/время] и отвечает за скорость процесса биодеструкции, а параметр а имеет размерность [1/время²] и отражает величину ускорения или замедления процесса биодеструкции во времени.

При биодеструкции в качестве первичного продукта разложения (парааминофенол при биодеструкции парацетамола) кинетические уравнения с параметрами в линейной зависимости «константы» реакции от времени процесса сохраняют те же значения (по крайней мере для парааминофенола при биодеструкции парацетамола). Этот факт для парааминофенола отражен в результатах сравнения экспериментальных данных по биодеструкции парацетамола и системы кинетических уравнений для всех компонентов процесса (парацетамола, парааминофенола, уксусной кислоты и твердых остатков) [8].

Результаты данных исследований не противоречат теории кинетики химических процессов, хотя имеют свою специфику [10]. При микробиологическом окислении ароматических и гетероароматиче-ских соединений, которыми являются объекты настоящего исследова- ния, гидроксилирование обычно происходит в орто- и мета-положении ароматического кольца. Однажды гидроксилированное, оно становится легко атакуемым микроорганизмами, так как при гидроксилировании нарушается ароматичность молекулы. В связи с этим часто происходит дальнейшее окисление соединений, в результате которого раскрывается ароматическое кольцо.

Причиной этого является прежде всего доступность большей части продуктов расщепления ароматического кольца ферментам микроорганизмов. Продуктами реакций при орторасщеплении являются муконовые кислоты, а при метарасщеплении - муконовые полуальдегиды. Этот факт, естественно, можно установить только экспериментально.

Для разработки кинетических уравнений необходимы именно экспериментальные данные по биодеструкции исследуемых соединений в зависимости от времени процесса.

2.    Биомеханика биодоступности мягких желатиновых капсул

Желатиновая оболочка состоит из желатина, воды и пластификатора. Для её получения используется раствор желатина - ограниченно набухающего высокомолекулярного вещества, который представляет собой гелеобразную вязкую жидкость, как и гидрофильный наполнитель капсулы - полиэтиленгиколь-400.

Используется кинетическое уравнение нулевого порядка, что отражает постоянную скорость изменения влажности наполнителя, оболочки и капсулы в целом.

d ^ d t

- K

акт,пас

сушки ,

где ф, %/ч - влажность; t , ч - время.

Результаты кинетического анализа приведены в табл. 2.

Таблица 2

Значения скорости сушки в активном и пассивном периодах

Период сушки	Скорость сушки, % / ч
	Капсула	Оболочка	Наполнитель
Активная сушка	1,004	14,280	–3,360
Пассивная сушка	0,061	0,086	0,065

Знак минус в активном периоде сушки отображает повышение влажности наполнителя за счет поступления в него влаги от более влажной оболочки. Перед завершением активного периода направление движения влаги изменяется - от наполнителя через оболочку в окружающую среду, то есть приобретает привычный для сушки однородных материалов вид. Скорость сушки оболочки, наполнителя и капсулы в целом при естественной сушке в пассивном периоде на один-два порядка ниже, чем в активном периоде.

Потребительские и технологические свойства гелей характеризуются прилипаемостью, намазываемостью, а также механическими показателями вязкой жидкости - механической и динамической вязкостью, предельным напряжением сдвига, наличием и формой петли гистерезиса в координатах «напряжение сдвига - скорость сдвига» [2-5].

В процессе формования в результате температурного воздействия получается мягкая желатиновая оболочка с влажностью 38-41,5 %, которая представляет собой вязкоупругое тело. Оболочка, высушенная до влажности 10-15 %, становится жесткой и хрупкой - на первый взгляд - практически упругим телом.

В процессе активной сушки и шлифовки во вращающемся барабане, а также при хранении нерасфасованных капсул они испытывают механические воздействия, которые могут приводить к потере формы, разрыву оболочки и вытеканию наполнителя. В связи с этим представляет интерес реология желатиновой оболочки, в первую очередь жес-костные характеристики - модуль упругости и коэффициент Пуассона в начальной стадии нагружения.

Для экспериментального исследования из пластинчатых желатиновых заготовок с применением стандартного ножа вырубали образцы IV типа с укороченными уширениями (рис. 1, а ) шириной 2,03 мм в базовой области. Образцы устанавливали в цанговые захваты разрывной машины (рис. 1, б ). Испытания на растяжение проводили по ГОСТ 270-75 со скоростью 10 мм/мин до разрыва образца¹.

В зависимости от влажности значительно изменяются механические свойства желатиновой оболочки. Реальные значения влажности оболочки находятся в пределах от 41,5 % при формовании капсул до 35-38 % для готовых мягких желатиновых капсул и до 10-15 % для

Исследования проведены с помощью д. т. н. А.А. Адамова в ИМСС УрО РАН.

капсул с пересушенной (твердой) оболочкой. Следует отметить, что мягкая желатиновая оболочка распадается в воде при температуре 36 ° С в течение 10 мин, а пересушенная оболочка - в течение 15 мин, что в обоих случаях соответствует требованиям фармакопеи по показателю «Распадаемость» [10].

а                б

Рис. 1. Стандартные испытания желатиновой оболочки на растяжение: а - подготовленный образец оболочки; б - образец в цанговых захватах машины в момент разрыва

В связи с этим испытаниям на растяжение подвергали образцы желатиновой оболочки с различной влажностью.

На рис. 2 представлены результаты растяжения образцов желатиновой оболочки с влажностью 15 % на момент испытания. Толщина вырубленных образцов составляла 0,55-0,57 мм с базовым размером 18 мм. Для определения модуля упругости использовали интервал по напряжениям в пределах от 2 до 6 МПа в начальной стадии нагружения (рис. 2, а ). Модуль Юнга находится в пределах от 446 до 511 МПа. Среднее его значение для пересушенной желатиновой оболочки составляет 480 МПа, что определяет достаточно высокую жесткость для материалов подобного типа.

Полная кривая растяжения при испытании жесткой желатиновой оболочки на разрыв представлена на рис. 2, б. Материал оболочки находится в упругом состоянии при деформации в пределах 6-10 %. Наибольшее сопротивление деформации составляет 32,8-35,6 МПа. Среднее значение данной величины оср = 480 МПа можно считать пре- делом прочности жесткой оболочки. Однако материал проявляет достаточно высокие вязкие свойства и не разрушается до деформации порядка 16-34 %. Момент разрушения образца жесткой оболочки показан на рис. 2, б.

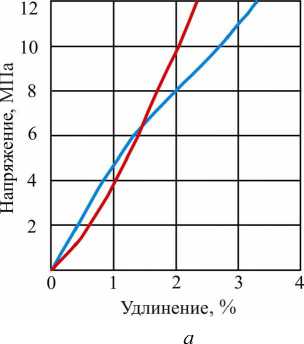
Рис. 2. Кривые растяжения образцов желатиновой оболочки с влажностью 15 %: а - в начале нагружения; б - при растяжении до разрыва

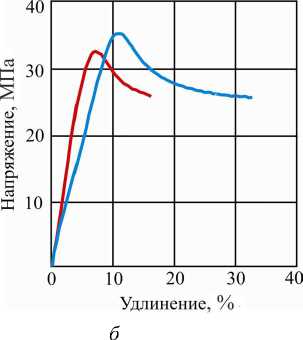
На рис. 3 представлены результаты растяжения образцов желатиновой оболочки с влажностью 38 % на момент испытания. Толщина вырубленных образцов составляла 0,95-1,10 мм с базовым размером 15 мм. Для определения модуля упругости использовали интервал по напряжениям в пределах от 0,5 до 2,0 МПа в начальной стадии нагружения (рис. 3, а ). Модуль Юнга находится в пределах от 39,9 до 40,1 МПа. Среднее его значение для мягкой желатиновой оболочки составляет 40 МПа, что на порядок ниже, чем для материала пересушенной оболочки.

Полная кривая растяжения при испытании мягкой желатиновой оболочки на разрыв представлена на рис. 3, б . Материал оболочки находится в упругом состоянии при деформации до 4-5 % (см. рис. 3, а ), а при расчетах состояния оболочки с большими деформациями можно считать, что до 10 %.

Мягкая желатиновая оболочка при нагружении ведет себя, как материал с упругопластическими свойствами. Предел текучести о0,2 = 2,8-3,0 МПа. Предел прочности находится в интервале 5,87,5 МПа, среднее значение предела прочности оср = 6,7 МПа. После достижения предела текучести мягкая желатиновая оболочка, испытывая близкое к линейному упрочнение, разрушается при деформации порядка 150-190 %.

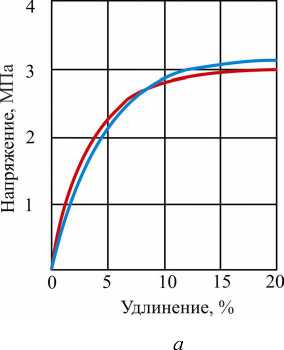
Рис. 3. Кривые растяжения образцов желатиновой оболочки с влажностью 38 %: а - в начале нагружения; б - при растяжении до разрыва

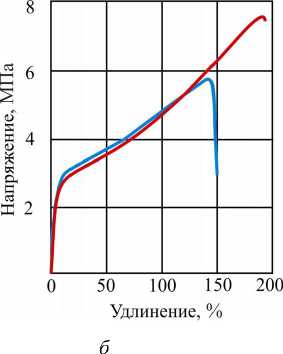
Время растяжения до разрушения жесткой желатиновой оболочки составляет порядка 20-30 с, мягкой - 140-170 с. При этом следует отметить 1,5-2-кратный запас удлинения без разрушения материала мягкой желатиновой оболочки.

Коэффициент Пуассона желатиновых оболочек, полученных путем сушки до рассмотренных пределов остаточной влажности, имеет значение порядка 0,497. При анализе деформации в нестесненных условиях коэффициент Пуассона можно считать практически равным 0,5, то есть желатиновые оболочки являются практически несжимаемым материалом.

3.    Заживляемость мягких тканей

Кожа, жировая ткань и мышечная ткань имеют разную заживляемость после операционного вмешательства. Например, липосакция жировой ткани на огромных площадях и хорошее заживление после косметической операции, т.е. заживление соприкасающихся остатков жировой ткани на коже изнутри и на мышцах снаружи.

Похоже, что ^кож > —— > xXмыш , dt       dt       dt т.е. скорости заживления

уменьшаются в этом направлении. Возникает вопрос о хирургических швах (рис. 4).

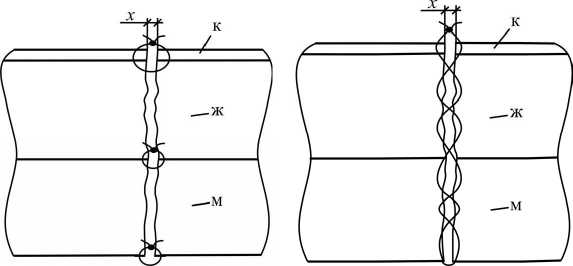
а                            б

Рис. 4. Схема хирургических швов по толщине: а - традиционный; б - из идеи хорошей заживляемости жировой ткани; х - расстояние между живыми тканями в каждой точке по длине; ^Т" - узел; ^S - хирургическая нить

Для кожи, жировых тканей и мышц ткани в конкретной точке по длине шва можно предположить, что скорость уменьшения х (скорость заживления, регенерации ткани) обратно пропорциональна ширине зазора между сшитыми тканями (рис. 5) (при уменьшении ширины сначала кровяной сгусток, затем развитие ткани и его выталкивание или преобразование должны идти интенсивнее).

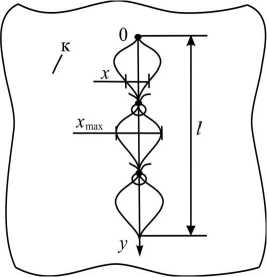
Рис. 5. Схема хирургического шва по длине разреза: 'V' - узел; <5 - хирургическая нить; l - общая длина; х как функция от у -зазор между сшиваемыми тканями; х max - максимальный зазор в промежутках между узлами

Для каждого типа тканей можно тогда записать кинетическое уравнение заживления шва dx dt

- 5 , x

где 5 - коэффициент, определяемый экспериментально для каждого типа тканей, кож ,

5 - А

S жир ^,

J X d ^x = ^{- 5} Jd t; у £ = ^{- 5} 0 ; 2 ^- у ^-- st 2

x 0	0
или	22 x 0     x t - 2 5  2 5 "
Обозначив	x 2 время заживления как 25 = t заж , получим зависи-
мость x ( t ):	t = t   -X— .                          (5) заж 2 5

S . ° мыш

Уравнение (3) легко интегрируется (пусть 5 пока равно const), тогда

x	t          22 x x        t x    x 0

Рассмотрим связь (5) между шириной заживающего шва и временем. Эта зависимость проиллюстрирована на рис. 6.

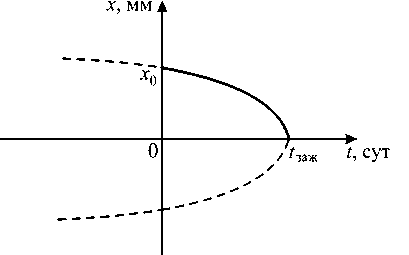
Рис. 6. Зависимость ширины заживающего шва от времени: ----нефизическая часть графика; х ₀ - начальная ширина шва; t _заж - время заживления

Соотношение (5) и кривая на рис. 6 отражают тот факт, что заживление идёт сначала медленно, но со временем скорость нарастает до максимальной при окончании процесса.

Замечание . Вопрос о S = const и виде кинетического уравнения заживления (3) можно решить только экспериментально, в частности по литературным данным.

Имея кинетические кривые для всех трёх типов тканей вида (5), можно попытаться мотивировать необходимость шва не только в областях стыков кожной и мышечной тканей (см. рис. 4, а ), но и жировой ткани (см. рис. 4, б ).

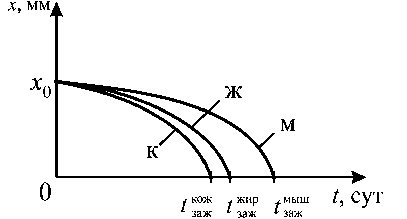
Рис. 7. Кинетические зависимости заживления шва для кожной - к , жировой - ж и мышечной - м тканей

Неизвестно, какая из тканей регенерируется в швах быстрее, но, нормируя величины стягивания тканей нитями (т.е. задавая x max при сшивании), можно подобрать на основе кинетических кривых (рис. 7) такие послеоперационные зазоры между тканями х ™^ж, х j^, х ™^ш, чтобы управлять процессом заживления: какая заживет первой по порядку и по времени.

Пусть из медицинских соображений следует, чтобы сначала заживала мышечная ткань (инфильтрат выдавливается через зазоры в жировой и кожной тканях), затем жировой слой (инфильтрат выдавливается через уменьшающийся зазор в кожной ткани), последней заживает кожная ткань. То есть следует реализовать условие t s’¹™ >  t _з™^р >  t з™ • Тогда кинетические кривые следует расположить в порядке, представленном на рис. 8.

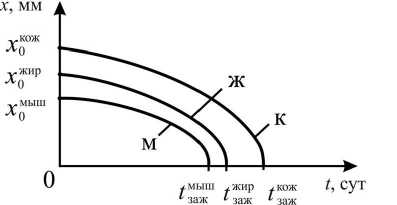
Рис. 8. Кинетические кривые заживления хирургических швов в предложенном алгоритме

Из соображений поддерживания постоянного оттока инфильтрата под х К^ож , х 0™^р , х М^ыш следует понимать максимальные величины зазоров между тканями в промежутках между узлами на нитях (см. рис. 5).

В результате исходя из общего времени заживания послеоперационного шва t к™, опережения заживления жировой ткани Л t ^кож = t ,'ЖЖ - t, и опережения заживления мышечной ткани жир заж заж

ЛtмыШ = tжжр - tз™ (или исходя из времени заживления внутренней мышечной ткани t™ш, что в данном алгоритме последовательности заживления выглядит правильней) на основе кинетических уравнений типа (3) можно определить максимальные между узлами нитей зазоры между сшиваемыми тканями: хкож - для кожи; хжир - для 0max                              0max жировой ткани и хмыш - для мышечной ткани. 0max

4.    Эффективность применения кинетических уравнений на примере биодеструкции

Можно ввести критерии окончания эксперимента при исследовании процесса биодеструкции исходного субстрата или продукта его разложения практически до нулевой концентрации, а также при биодеструкции с целью достижения заданного значения ПДК.

После интегрирования кинетического уравнения (1) легко определяется время окончания процесса t _пр :

t пр

- b+ b ² - 2 aln^ x ₀

a

Параллельное экспериментальным измерениям кинетическое моделирование процесса биодеструкции позволяет заметно снизить объем и продолжительность эксперимента, особенно для новых объектов исследования. Уже по исходной концентрации и по следующим через равные промежутки времени двум экспериментальным точкам моделирование позволяет получить начальное приближение параметров переменной «константы» скорости реакции, оценить кинетическую кривую в начальном приближении и время окончания процесса биодеструкции по значению ПДК. Последующие пробы культуральной жидкости необходимы с целью уточнения указанных характеристик [9].

Идея параллельного кинетического моделирования может быть применена для других биологических процессов, определяющие параметры которых можно отследить во времени (например, при регулярном посещении врача). При этом можно разработать биомеханическое сопровождение процесса индивидуального лечения конкретного пациента.

Выводы

• 1.    Ддя производных изохинолина, фенола и карбоновых кислот показана адекватность кинетической модели, представляющей собой уравнение первого порядка с переменными «константами» скорости реакции, процессу биодеструкции лекарственных средств актинобактериями рода Rhodococcus . Параметры переменной «константы» отражают, помимо скорости, замедление процесса биодеструкции во времени.

• 2.    Введены критерии окончания эксперимента при исследовании процесса биодеструкции исходного субстрата или продукта его разложения практически до нулевой концентрации, а также при биодеструкции с целью достижения заданного значения ПДК. На основе параллельного кинетического моделирования можно прогнозировать течение процесса по первым трем экспериментальным данным с дальнейшим уточнением при появлении новых точек.

• 3.    Биологическая доступность мягких желатиновых капсул зависит от первоначальной и окончательной влажности оболочки. Показано, что уменьшение влажности желатиновой оболочки с 38 до 15 % увеличивает время распада капсул в воде с 10 до 15 минут. Это свидетельствует об уменьшении биодоступности с уменьшением влажности капсул в указанных пределах, но соответствует требованиям фармако-

• пей, что обеспечивает эффективное использование указанных биологически активных добавок и лечебных грязей.

• 4.    Определены механические свойства желатиновой оболочки с разным содержанием влаги. В результате эксперимента на растяжение установлено, что мягкая желатиновая оболочка при деформации проявляет свойства упругопластического тела с упругой областью до 10 % и с удлинением до разрушения порядка 150-190 %. Уменьшение остаточной влажности оболочки повышает жесткость, увеличивает предел прочности, не ужесточая при этом требований к технологии формования, шлифования и сушки капсул.

• 5.    Предложены теоретические предпосылки по кинетике заживления мягких тканей человека в послеоперационный период.