Кинетическое моделирование пристеночного слоя плазмы стационарного плазменного двигателя

Стационарный плазменный двигатель (СПД) является наиболее активно используемым в России типом электроракетных двигателей [1]. Разрядная камера СПД может быть либо полностью выполнена из керамики, либо иметь металлические стенки в прианодной области и керамические кольца на срезе разрядного канала. В данной работе рассматривается вариант СПД с составной разрядной камерой, содержащий как металлические, так и керамические элементы (рис. 1). Наиболее детальные исследования особенностей работы этой схемы СПД проведены в [2]. Основная задача изолятора заключается в ограничении области горения разряда и предохранении металлических элементов конструкции двигателя от контакта с плазмой. В результате взаимодействия плазмы с диэлектрической поверхностью образуется пристеночный слой. Процессы, протекающие в пристеночном слое, оказывают существенное влияние на работу двигателя в целом.

Рис. 1. Схема разрядного канала СПД: 1 — изоляционные кольца, 2 — анод-газораспределитель, 3 — магнитные катушки, 4 — металлическая анодная камера

Пристеночная проводимость является одним из механизмов транспорта электронов к аноду перпендикулярно магнитному полю [3, 4]. Величина пристеночной проводимости определяется структурой пристеночного слоя и интенсивностью вторичной электрон-электронной эмиссии (ВЭЭЭ). Эта интенсивность в свою очередь оказывает влияние на положение ускоряющего слоя в разрядном канале [5].

Вторичные электроны, образованные в результате бомбардировки поверхности диэлектрика. первичными электронами, имеют относительно небольшую энергию. Таким образом, интенсивная ВЭЭЭ приводит к охлаждению электронной компоненты плазмы и влияет на. структуру разряда в канале СПД.

Величина падения потенциала в пристеночном слое вносит вклад в энергию ионов, бомбардирующих поверхность, и оказывает влияние на интенсивность эрозии изоляторов. В математических моделях [6-8], описывающих работу СПД в целом, процесс взаимодействия плазмы с поверхностью изолятора учтен не достаточно полно. Мы считаем, что для создания новых и улучшения существующих моделей СПД необходимо тщательно изучить физику процессов, протекающих в пристеночной области. Поскольку экспериментальное исследование пристеночных процессов в СПД затруднено, для их детального исследования целесообразно прибегнуть к численному моделированию. В настоящее время существуют различные подходы к исследованию взаимодействия плазмы стационарного плазменного двигателя с материалом изолятора. [9-11]. Однако авторами таких работ не учитывается влияние магнитного поля на. пристеночный слой. Также при описании процесса. ВЭЭЭ пре-небрегается зависимостью коэффициента, вторичной эмиссии от угла, падения первичных электронов.

В данной работе проводится анализ влияния локальных параметров плазмы, свойств материала, изолятора, величины и направления магнитного поля на. структуру пристеночного слоя. Для этого была, создана, одномерная по координате и трехмерная по скорости кинетическая модель, которая включает в себя вторичную электрон-электронную эмиссию и учитывает влияние магнитного поля. При описании ВЭЭЭ учитывается зависимость ее интенсивности как от энергии, так и от угла, падающих на. поверхность частиц.

Классическая теория пристеночного слоя [12], основанная на. предположении о том, что электроны имеют максвелловское распределение, позволяет определить величину перепада потенциала, и другие параметры слоя. Согласно этой теории на. входе в слой ионы имеют так называемую бомовскую скорость:

и концентрацию

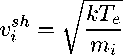
nf1 = 0, 61n,1, i где Те — температур а электронов, mi — масс а иона, n, — концентрация ионов в плазме, к — постоянная Больцмана. Область, в которой ионы ускоряются до бомовской скорости, принято называть предслоем. Условия равенства потоков ионов Ji и электронов Je на поверхность позволяют получить выражение для потенциала, поверхности при отсутствии вторичной электронной эмиссии [12]:

_у5Иг -^1 = ^кТ _ь (о , 61^2^} ,                     (2)

где у^р/ — потенциал плазмы, m_e — масса электрона. Это выражение может быть использовано для проверки математической модели при отсутствии вторичной эмиссии.

Интенсивность процессов ВЭЭЭ определяется экспериментально [13] путем бомбардировки поверхности электронным пучком и измерения обратного потока, электронов. Исходя из энергии вторичных электронов, их разделяют на. три группы: упруго отраженные электроны, истинно вторичные электроны и неупруго отраженные электроны. Определить строгую границу между истинно вторичными и неупруго отраженными электронами невозможно. При достаточно больших энергиях первичных электронов (сотни электронвольт и более) неупруго отраженными электронами считаются те, чья энергия превышает величину 50 эВ [14].

Таким образом, коэффициент ВЭЭЭ ст может быть представлен как сумма коэффициента истинной вторичной эмиссии 6, коэффициента неупругого отражения ту и коэффициента упругого отражения г:

ст = 6 + ту + г.

Как отмечают авторы экспериментальных работ [13, 14], посвященных исследованию ВЭЭЭ, процессами неупругого отражения электронов при малых энергиях (до 1 КэВ) можно пренебречь. Вероятность упругого отражения при характерных для СПД энергиях (до 100 эВ), как правило, слабо зависит от энергии первичных электронов и для различных диэлектриков может принимать значения в пределах от 0,05 до 0,2 [14].

Экспериментальное исследование вторичной эмиссии при бомбардировке диэлектрика, моноэнергетичным пучком электронов [14] показывает, что при малых энергиях (до 100 эВ) величину 6 можно представить как произведение двух независимых величин:

6(а, е) = 6(а)6(е), где а — угол падения пучка на поверхность, е — энергия пучка. При характерных для СПД электронных температурах, не превышающих 100 эВ, функция монотонно возрастает [14]. Она. приближенно может быть описана, зависимостью следующего вида. [15]:

6(e) = (І) ■ где Ei — величина первого порога размножения электронов, А — коэффициент, зависящий от свойств материала.

Экспериментальные исследования [13] показывают, что интенсивность ВЭЭЭ существенно зависит от угла падения частиц на поверхность материала. В данном случае под углом падения понимается угол между скоростью бомбардирующей частицы и нормалью к поверхности. Возрастание интенсивности эмиссии при увеличении угла, падения объясняется авторами исследования [13] следующим образом. При наклонном падении электроны будут проникать в вещество на. меньшую глубину, чем при нормальном падении, сохраняя длину пробега, внутри вещества. Следовательно, вторичные электроны будут возникать на. меньшей глубине и имеют больше шансов выйти наружу.

Используя исследования, проведенные в работе [16], зависимость 6(а,е) можно представить в виде

6(а, е ) = exp

(3 у(1

-

cos а )^

6 ( e ) = exp

(3 у(1

-

^cos “ ’)(f) ■

где у — коэффициент, значение которого, полученное авторами работы [16], приблизительно равно 0,5.

Таким образом, выражение (3) описывает зависимость коэффициента, истинной вторичной эмиссии при бомбардировке поверхности материала, моноэнергитичным пучком электронов под определенным углом.

2.    Кинетическая модель пристеночного слоя плазмы

Для исследования влияния параметров плазмы, свойств материала, и внешних полей на. формирование пристеночного слоя и процессы, протекающие в нем, была, создана, математическая модель. Современные модели плазмы можно разделить на. три основные категории: гидродинамические модели, гибридные модели и кинетические модели [7,17,18]. Для решения данной задачи наилучшим образом подходит кинетический метод «частица, в ячейке». Данная модель является одномерной по координате и трехмерной по скорости.

Областью моделирования был выбран пристеночный слой плазмы. Толщина, моделируемой области была принята на порядок большей радиуса Дебая. Ось X направлена по нормали к поверхности, ось Ү сонаправлена с осью двигателя, ось Z имеет направление азимутальной касательной к поверхности (рис. 1). Границами области моделирования являются поверхность диэлектрического материала, с одной стороны, и условная граница, между слоем и плазмой, на. которой ионы достигают бомовской скорости (т. е. граница, слой-предслой), с другой стороны.

Плазменные компоненты описывались как большое число моделирующих частиц. Нейтральными атомами и двухзарядными ионами пренебрегалось. В одномерной кинетической модели моделирующая частица, представляет собой бесконечную равномерно заряженную плоскость. При этом поверхностная плотность заряда Ө и поверхностная плотность массы ц этой моделирующей частицы будут связаны следующим образом:

ц _ т

Ө ^— 7’

Здесь т и е — масса и заряд соответствующих реальных частиц (электронов либо ионов). При моделировании заряд частиц-электронов и заряд частиц-ионов задавались одинаковыми по модулю.

Для того чтобы модель достоверно описывала, данное физическое явление, на. нее были наложены следующие условия [19]:

Аж « Rd ,(4)

Ө « пр/еАж,(5)

At «ш-1.(6)

Здесь Аж — ширина ячейки, Rd — радиус Дебая, At — время, моделируемое одной итерацией, шр — плазменная частота. Неравенство (4) — это требование достаточной мелкости разбиения моделируемой области. Неравенство (5) — условие достаточной плотности моделирующих частиц в ячейках. Неравенство (6) необходимо для корректного описания самосогласованного движения моделирующих частиц в рамках нестационарной кинетической модели.

Распределение потенциала р(ж) вдоль координаты ж на каждой итерации находилось в одномерном приближении путем решения уравнения Пуассона:

а²р(ж)       р(ж)

-- —~— —--.

^ж2         Ео где р(ж) — плотность заряда, определяемая распределением моделирующих частиц. Разностная схема, используемая для этого, имела, следующий вид:

W-1 ^— 2W + Р к+1 _— - Pfe

Аж2              Е0 ’ где р л р^ — значение потенциала, и плотности заряда, в к-м узле сетки.

Для решения уравнения (7) было задано два. граничных условия. Первое граничное условие — фиксированное значение потенциала, на. границе слой-предслой, определяемое из критерия Бома:

Яж)|"“ — рр — 2    .

Второе граничное условие определяется из предположения о том, что вся система, поверхность-слой-предслой-плазма электрически нейтральна, т. е. в диэлектрике электрическое поле отсутствует. Значение производной потенциала, на. поверхности диэлектрика:

арж ^sur _— - ө^

аж            Ео '

где Ө^8ит — плотность поверхностного заряда стенки, которая определяется на каждой итерации при взаимодействии моделирующих частиц с этой границей. Для Дй итерации значение этой величины определяется следующим образом:

Ө8™ |. = ^т |,-1 + £ Ө, где суммирование производится по всем ионам и электронам, которые «погибли» на. поверхности за. итерацию.

Вешнее магнитное поле в модели задавалось двумя компонентами:

В = (В_ж,Ву , 0).

Поскольку характерные размеры области моделирования малы по сравнению с геометрическими размерами СПД, с достаточной точностью можно полагать, что в рамках данной задачи величина, и направление магнитного поля не зависят от координат.

Движение моделирующих частиц-ионов описывалось как одномерное и происходило относительно оси X. Таким образом, для каждой моделирующей частицы-иона на каждой итерации определялась координата x и скорость -щ. Поскольку магнитное поле оказывает существенное влияние на движение электронов, а значит, и угол их падения на поверхность, значение которого важно для описания процесса. ВЭЭЭ, для моделирующих частиц-электронов на каждой итерации определялось три компоненты скорости: -щ, г_у и щ.

Движение ионов описывалось уравнением d2x

mi dt2

dip dx

Движение электронов описывалось системой уравнений

' me	d2x	_ ( dp dz \ - + dty) ,
е	dt2
me	d2y	= (-»•
е	dt2
me	d2z	- (-^+>	)︂
„ е	dt2

Вычисления координат и скоростей моделирующих частиц производились с помощью схемы Бориса [19].

В данной модели принималось максвелловское распределение электронов по скоростям в плазме на. границе области моделирования. Для стационарного плазменного двигателя это является весьма грубым приближением [20]. Тем не менее оно было принято в данном исследовании, целью которого является оценка, степени влияния различных параметров на. пристеночный слой. Такое предположение позволяет проверить работу модели для классического случая, описанного выше. Поскольку пристеночный слой и разряд стационарного плазменного двигателя, как отмечалось выше, оказывают друг на. друга, сложное взаимное влияние, то более точное моделирование пристеночного слоя плазмы СПД возможно только в рамках моделирования двигателя в целом.

Поток частиц из плазмы в пристеночный слой моделировался путем добавления новых моделирующих частиц в окрестности соответствующей границы области на. каждой итерации. Скорость ионов определялась выражением (1). Скорость электронов выбиралась случайной с учетом максвелловского распределения. Число новых моделирующих частиц за одну итерацию было таким, чтобы их поток в моделируемую область соответствовал бомовскому приближению.

При столкновении частиц с поверхностью моделировалось два. процесса: рекомбинация и вторичная электрон-электронная эмиссия. Моделирующие частицы-ионы на. этой границе «гибли» передавая свой заряд поверхности, изменяя величину Ө8™-. При столкновении моделирующих частиц-электронов с поверхностью происходило либо их упругое отражение, либо поглощение с эмиссией некоторого количества, вторичных частиц. Вероятность упругого отражения моделирующей частицы-электрона, определял коэффициент упругого отражения г, задаваемый как свойство материала. При поглощении моделирующей частицы поверхностью ее заряд также передавался поверхности. Кроме этого, с помощью выражения (3) вычислялся коэффициент истинной вторичной эмиссии. Сумма, коэффициентов вторичной эмиссии для всех столкновений на. протяжении одной итерации определяла, число вторичных моделирующих частиц-электронов. При эмиссии вторичных моделирующих частиц-электронов их заряд вычитался из заряда, поверхности. Скорости этих моделирующих частиц задавались так, чтобы соответствовать максвелловскому распределению. Их температура, задавалась значением 1-5 эВ [14].

3.    Результаты моделирования

При выполнении численных экспериментов, описанных далее, в качестве начальных условий задавались следующие величины: плотность плазмы n^pl и температура электронов Т_е в плазме, компоненты вектор а индукции магнитного поля В_ж и В_у, коэффициент упругого отражения электронов г и другие константы, характеризующие свойства материала изолятора, входящие в выражение (3), температура вторичных электронов Т^.

Первая серия численных экспериментов проводилась с целью сравнения результатов моделирования с известным точным решением для классического слоя. Поэтому в этой серии процессы ВЭЭЭ не моделировались. При этом задавалась плотность плазмы, характерная для СПД n^pl = 5,0• 1017 м^-3. Температура электронов в плазме для каждого расчета варьировалась.

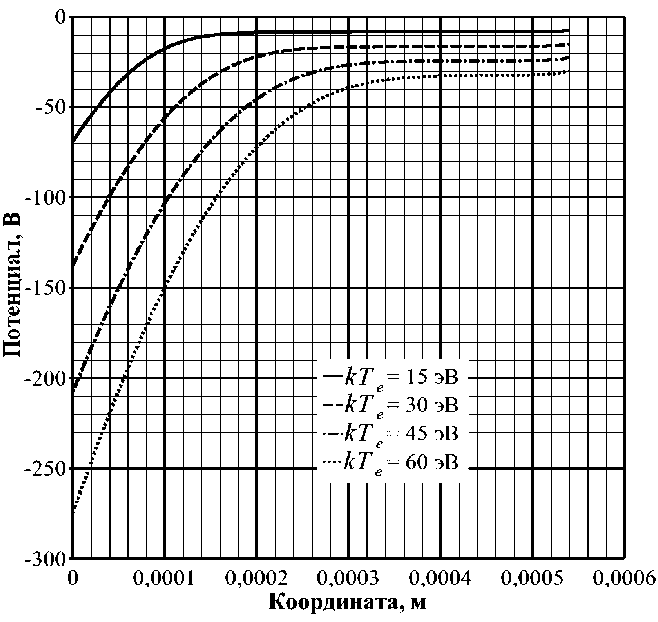
Рис. 2. Распределение потенциала, в слое при различной электронной температуре

На рис. 2 показано распределение потенциала, в области моделирования для различных значений температур. Величины пристеночного падения потенциала находятся в хорошем соответствии со значениями, полученными с помощью выражения (2). Сравнение резуль- татов моделирования с аналитическими значениями приведено в табл. 1. Наибольшее расхождение при различных параметрах составило около 3%.

Таблица!

Величина пристеночного падения потенциала

кТе, эВ	15,0	30,0	45,0	60,0
sUT — ф1, в (моделирование)	70	139	209	276
^suc — д^, в (аналитическое решение)	69,2	137,8	207,8	274,8
Относительное отклонение, %	1,08	0,36	0,6	ОД

Проанализировав структуру кривых, можно сделать вывод о зависимости между толщиной слоя Н. в котором происходит резкое падение потенциала, и радиусом Дебая Rd-Отношение этих величин у=R

В табл. 2 приведена зависимость относительной ширины слоя у от температуры электронов.

Т а б л и ц а 2

Зависимость относительной ширины слоя от температуры электронов

кТе, эВ	15,0	30,0	45,0	60,0
у	4,9	4,85	4,95	4,9

Можно сделать вывод о том, что соотношение между толщиной слоя и радиусом Дебая сохраняется при изменении температуры электронов.

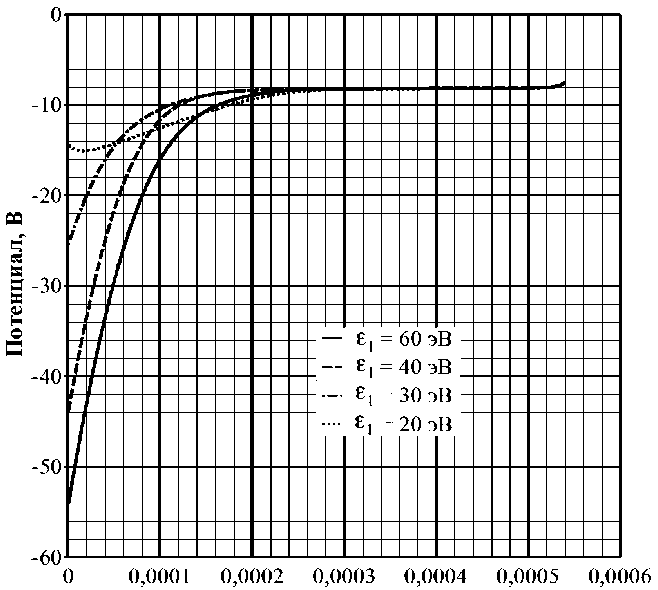
Координата, м

Рис. 3. Распределение потенциала, в слое при различной величине первого порога, размножения электронов

Вторая серия численных экспериментов была, направлена, на. исследование влияния ВЭЭЭ на. структуру пристеночного слоя плазмы. В этой серии были взяты характерные для керамики стационарного плазменного двигателя значения г = 0,1, у = 0, 5, А = 0, 576 [21]. В качестве величины первого порога, размножения электронов выбирались различные значения. Температура электронов в плазме кТ_е = 15, 0 эВ. На рис. 3. показано распределение потенциала, в моделируемой области при различной величине первого порога, размножения. В частности, видно, что толщина, слоя меняется слабо.

Отдельно следует заметить, что в последнем численном эксперименте, при относительно низкой величине первого порога, размножения электронов, произошло изменение структуры пристеночного слоя с образованием так называемого режима, насыщенного пространственного заряда [22]. Это связано с возрастанием интенсивности процесса ВЭЭЭ, которое приводит к тому, что поток вторичных электронов начинает превосходить поток первичных. В этом случае для образования стационарного слоя требуется наличие пространственного заряда, который, с одной стороны, отражает излишек электронов из плазмы обратно, а с другой — отражает часть холодных вторичных электронов к поверхности. При этом потенциал плазмы на. определенном расстоянии от поверхности, достигнув минимального значения, начинает возрастать. Поверхность в этом случае имеет положительный заряд.

Моделирование позволило исследовать влияние пристеночного слоя на функцию распределения электронов. В приведенном выше численном эксперименте определялась средняя энергия электронов ^E_eY покидающих область моделирования (табл. 3).

В табл. 2 приведена зависимость относительной ширины слоя у от температуры электронов.

Т а б л и ц а 3

Зависимость средней энергии электронов, покидающих слой, от величины первого порога размножения

Е 1 , эВ	Нет эмиссии	60,0	40,0	30,0	20,0
kEeY	14,98	14,91	14,66	13,23	10,70

Когда, интенсивность ВЭЭЭ отсутствует или незначительна, подавляющее большинство электронов отражается от пристеночного перепада потенциала и возвращаются обратно в плазму, не теряя энергии и не меняя своего распределения. Лишь малая часть электронов из «хвоста.» функции распределения поглощается стенкой. Потеря этих электронов приводит к слабому охлаждению электронной компоненты.

Наличие интенсивной ВЭЭЭ существенно меняет картину. Сниженный перепад потенциала. пропускает к поверхности больше электронов. В то же время к обратному потоку частиц добавляются холодные вторичные электроны, ускоренные в пристеночном поле. Это приводит к интенсивному охлаждению электронной компоненты.

При проведении численного эксперимента, фиксировалась функция распределения электронов по скоростям на. границе области моделирования (слой-предслой). Распределения электронов по проекциям скоростей на ось X при различной интенсивности процесса вторичной эмиссии показаны на. рис. 4. Здесь отрицательные скорости имеют частицы, проникающие в моделируемую область. Их распределение в соответствии с данной моделью задавалось как максвелловское. Положительные скорости имеют электроны, покидающие область моделирования. Эти электроны либо являются первичными и отразились от слоя, либо являются вторичными.

Из рис. 4 видно, что функция распределения электронов, покидающих область моделирования, отличается от исходной отсутствием частиц с высокой энергией (почти полностью лишена, «хвоста») и в то же время обладает вторым максимумом, соответствующим вторичным электронам, ускоренным в пристеночном слое.

Также с помощью данной модели был исследован процесс формирования пристеночного слоя при наличии магнитного поля. В первую очередь исследовалось влияние угла наклона

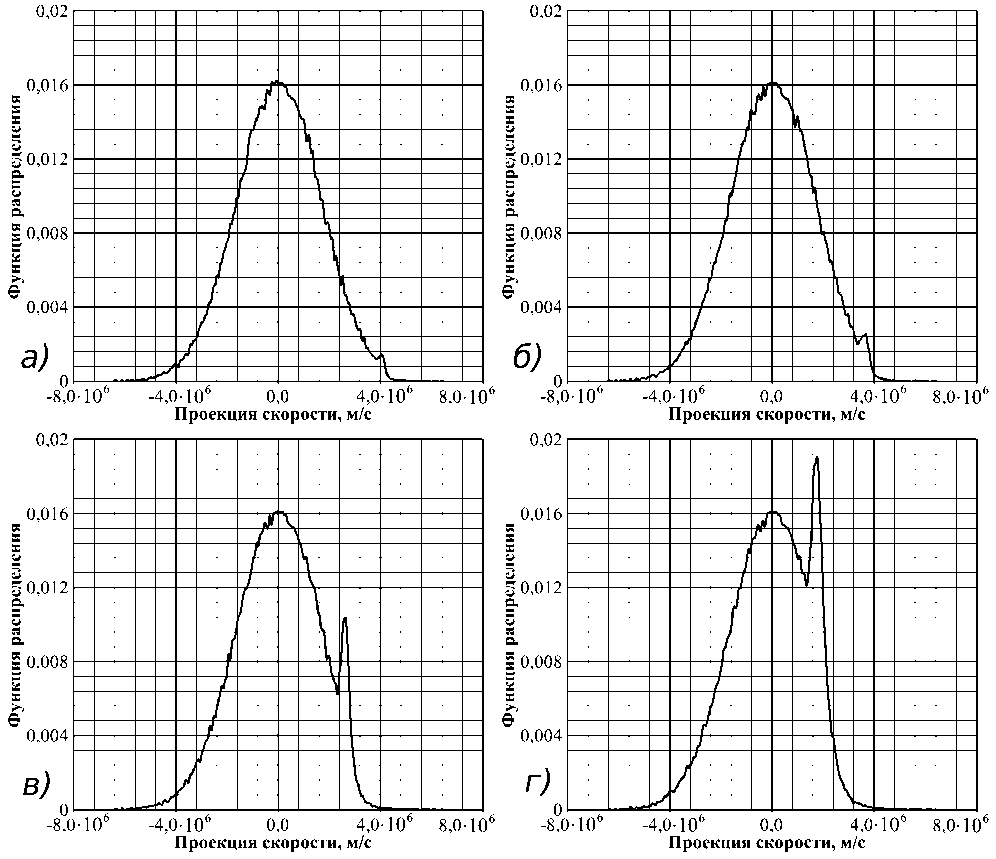
Рис. 4. Функции распределения электронов по скоростям а) £1 = 60 эВ, б) £1 = 40 эВ, в) £1 = 30 эВ, г) £1 = 20 эВ в направлении X на границе слоя.

магнитных силовых линий на величину пристеночного перепада потенциала, связанное с характером движения электронов. Механизм такого влияния заключается в следующем. В том случае, когда магнитное поле перпендикулярно поверхности, на преодоление разности потенциалов в слое электроны тратят энергию, приходящуюся только на одну степень свободы. Остальная энергия не может расходоваться при отсутствии столкновений, которые в данной модели не учитывались. При наклоне силовых линий магнитного поля проекция скорости электрона на нормаль к поверхности начнет изменяться. Это означает, что менее быстрые электроны смогут преодолеть перепад потенциала.

Таким образом, появление ненулевой компоненты магнитного поля, параллельной поверхности, приведет к тому, что на торможение электронного потока потребуется большая разность потенциалов. Чем больше величина этой проекции, тем быстрее электроны будут компенсировать потерто скорости в направлении оси X и соответственно тем сильнее возрастет пристеночное падение потенциала.

Для исследования этого явления изолированно от эффектов, связанных со вторичной эмиссией, проводились численные эксперименты, в которых процессы ВЭЭЭ не моделировались. Температура электронов и концентрация плазмы были приняты соответственно кТ_е = 15,0 эВ, n^pl = 5, 0 • 1017 м^-3. Были выполнены две серии численных экспериментов для магнитной индукции поля В = 400 Гс и В = 600 Гс, в каждой серии варьировался угол наклона силовых линий магнитного поля.

На рис. 5 показаны зависимости величины пристеночного падения потенциала от проек- ции магнитного поля на ось У для обеих серий экспериментов. Из рисунка можно сделать вывод о том, что величина, проекции магнитного поля на. тангенциальную к поверхности ось определяет степень влияния магнитного поля на пристеночный слой, в то время как полная индукция магнитного поля не столь важна.

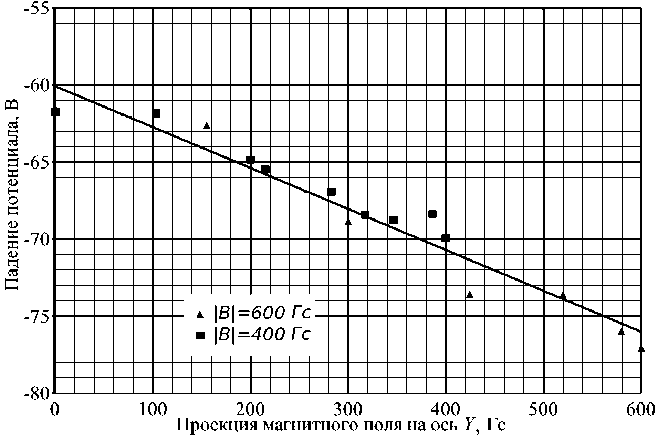
Рис. 5. Зависимость пристеночного перепада, потенциала, от проекции магнитного поля па. ось без учета. ВЭЭЭ

Также существует второй механизм влияния наклонного магнитного поля на. пристеночный слой. Этот механизм связан с явлением ВЭЭЭ и заключается в следующем. Интенсивность эмиссии вторичных электронов зависит от угла, падения первичных. При торможении в слое с магнитным полем, нормальным к поверхности, электроны, достигнувшие изолятор, имеют малую составляющую скорости по оси X, в то время как проекции их скоростей на оси У и Z сравнительно велики. Это означает, что углы, под которыми электроны падают на поверхность материала, зачастую близки к 90°. Однако при наклон ных силовых линиях магнитного поля углы падения электронов на. поверхность в среднем

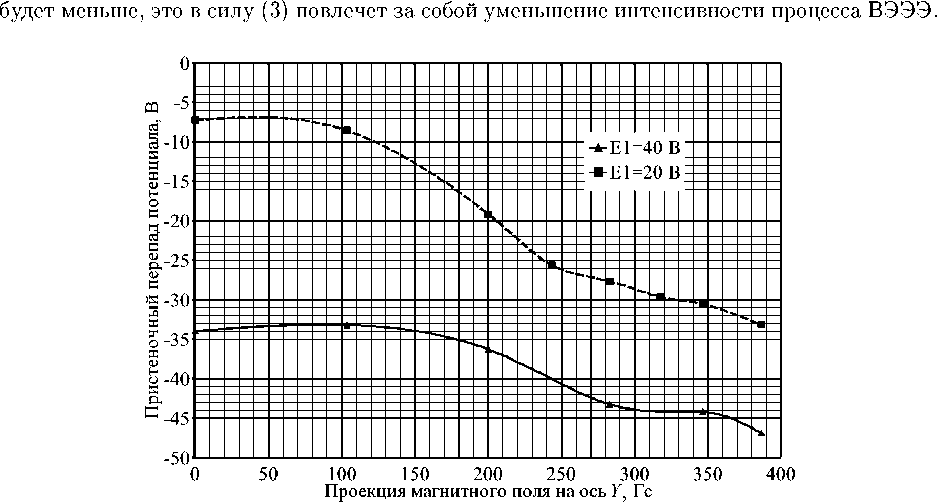
Рис. 6. Зависимость пристеночного перепада, потенциала, от проекции магнитного поля па. ось с учетом ВЭЭЭ

Для исследования этого явления были проведены две серии численных экспериментов. Температура, электронов и концентрация плазмы были приняты соответственно кТ_е = 15, 0 эВ, n^pl = 5, 0 • 1017 м^-3. Индукция магнитного поля В = 400 Гс. В первой серии величина первого порога размножения электронов была принята Ei = 40 эВ, во второй серии — E1 = 20 эВ.

Зависимости величин пристеночного перепада потенциала от проекции магнитного поля на ось У показаны на рис. 6. Проанализировав результаты моделирования, можно сделать вывод о существенном влиянии магнитного поля на. структуру пристеночного слоя плазмы. В частности, в случае с Ei = 20 эВ при наклоне линий магнитного поля 25° слой вышел из режима, насыщенного пространственного заряда, а. величина, падения потенциала, в слое возросла, в три раза.

4.    Заключение

Создана одномерная по координате и трехмерная по скоростям кинетическая FullPIC модель пристеночного слоя плазмы стационарного плазменного двигателя. С помощью модели проведено исследование влияния на. пристеночный слой различных параметров таких, как температура, электронов, концентрация плазмы, свойства, материала, стенки. Показано, что хотя интенсивность вторичной электрон-электронной эмиссии определяет структуру слоя, она не оказывает существенного влияния на его толщину.

Исследовано влияние пристеночного слоя на среднюю энергию и распределение электронов по скоростям. Показано, что интенсивная вторичная электрон-электронная эмиссия приводит к охлаждению электронов и существенно влияет на. их распределение по скоростям.

Проведено исследование пристеночного слоя плазмы в магнитном поле. Показано, что наклон магнитного поля оказывает влияние на. интенсивность вторичной электрон-электронной эмиссии и величину пристеночного перепада потенциала.

Результаты данного исследования могут быть полезны при создании двух- и трехмерных кинетических моделей стационарного плазменного двигателя, в которых так или иначе необходимо учитывать взаимодействие плазмы с поверхностью изоляционных колец.