Кинетика бейнитного превращения в малоуглеродистых сплавах железа

В работе [1] было показано, что специфические особенности строения пакетного мартенсита -иерархической структуры, где отдельные кристаллы рейки группируются в блоки и далее в пакеты -должны оказывать влияние на кинетику аустенит—>мартенситного превращения. Бейнит, особенно в сплавах с низким содержанием углерода, также представляет собой сложно организованную пакетную структуру, поэтому можно ожидать, что подобные особенности должны наблюдаться и для него.

Кинетику превращения в мы описывали при помощи уравнения Аврами

/ = 1-ехрН&”), (1) где / - доля превращения, t - время изотермической выдержки, а К и и -коэффициенты. Как показано в [1], для иерархической пакетной структуры показатель и должен уменьшаться в ходе превращения от 2 или 3 до 1.

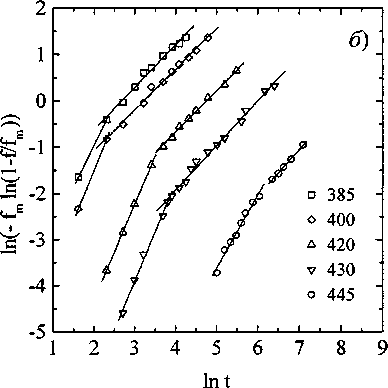
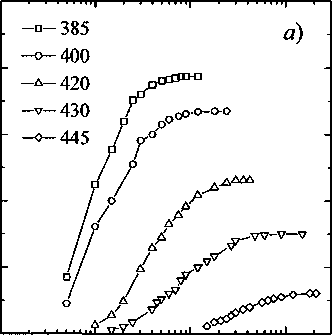
На рис. 1, а приведены кинетические кривые образования бейнита в сплаве Fe-9 % Сг, содержащем 0,09 % С (09X9) [2]. На рис. 1, б они, аналогично [1], представлены в двойном логарифмическом масштабе, что позволяет найти коэффициенты и и К:

In -A in

= 1п£+и1пГ

(здесь А - предельная доля превращения при данной температуре). На графиках действительно наблюдается изменение наклона; значения коэффициентов пи К приведены в таблице.

В отличие от мартенситного, при бейнитном превращении скорость роста отдельного реечного кристалла имеет конечную величину. Тогда, например, для и=2 параметр К будет равен

к=Ш,

1,0

0,8

0,6

0,4

0,2

0,0

1        10       100      1000

t, с

Рис. 1. Кинетические кривые образования бейнита в сплаве 09X9: а - в линейном масштабе; б - в двойном логарифмическом масштабе. Температуры превращения (в °C) указаны на рисунке

Таблица 1

Значения предельной доли превращения fm и коэффициентов п и In К для сплава 09X9 при различных температурах

Температура, °C	А	Значения коэффициентов в выражениях
		(2)		(18)
		п	1пХ	п	In Л"
385	0,775	1,81/0,91	—4,57/—2,44	2,20/1,00	—4,95/—2,40
400	0,67	2,19/0,88	—5,86/—2,82	2,19/1,00	—5,86/—3,04
420	0,462	2,08/0,90	—8,46/—4,27	2,08/1,00	-8,46М,61
430	0,30	2,13/0,97	—10,3/-5,81	2,13/1,00	-10,3/—5,91
445	0,122	1,59/1,01	—11,6/-8,10	2,00/1,00	-13,5/-8,01

Примечание: в числителе указаны значения на первом этапе превращения, в знаменателе - на втором этапе.

если автокаталитическое зарождение является более медленным процессом, чем рост рейки, и

К = к_г1_н<Вр1_р                              (4)

в противном случае. Здесь /_н - скорость независимого зарождения первых реек пакета; 7_а - скорость автокаталитического зарождения элементов пакета; Гор - скорость роста реечного кристалла в длину; /_р и К_р - его средняя длина и объем. Через к_х и к_г обозначены численные коэффициенты.

По поводу соотношения процессов зарождения и роста при бейнитном превращении в литературе встречаются разные мнения. По мнению Хиллерта [3], хотя рейки в макрокристалле и объединены автокаталитическим зарождением, но лимитирующим процессом является все же рост. Бхадешиа [4], напротив, полагает, что рост субъединиц происходит с большой скоростью, а кинетика превращения аустенит—>бейнит лимитируется зарождением. Авторы данной работы считают, что обе точки зрения можно примирить, если, во-первых, для кинетического коэффициента К использовать формулу (3), отражающую эффект автокаталитического зарождения субъединиц бей-нитной пластины [5, 6], а во-вторых, в гипотезе Бхадешиа учесть, что скорость зарождения зависит от вероятности перехода атома через межфазную границу (Р₊-Р_), где Р+ - вероятность присоединения атома к растущему зародышу, а Р_ - вероятность обратного перехода [7]. Добавление атома к зародышу на площади с? вызывает увеличение объема на с^, то есть продвижение фронта превращения вперед на расстояние d, чему соответствует скорость

®=d(P₊-P_),                       (5)

где d примерно равно межатомному расстоянию. Так как вероятность (Р+-Р-) пропорциональна скорости роста, то скорость независимого и автокаталитического зарождения также должна быть пропорциональна скорости роста. Мы будем определять их следующим выражением:

I_H4Njd>ex^-W[RTV        (6, а)

I_a = (Njd^exp^W-E^/RT^,      (6, б)

где N_H и N_a - количество соответствующих потенциальных мест зарождения в единице объема, Ж -энергия активации зарождения, а величина Е учитывает автокаталитический эффект.

Энергетический барьер зарождения в рамках теории Кауфмана-Коэна [8] можно записать как

W = WO-^^G = Ф-^^G-^GSY      д^

где AG - изменение свободной энергии при образовании новой фазы, a AG_S - термодинамический стимул превращения при Т=Т_# который отражает необходимость энергетических затрат для начала превращения. Хиллерт [9], приняв во внимание возможность обратных переходов атомов через границу, предложил заменить в (6) множитель

/   / dti л Г Ф kG—AG ехр(-Ж/7?Г) на Вехр ——--L- v RT) RT

Бейнитный феррит, образующийся в сталях, имеет, как правило, концентрацию углерода х“ более низкую, чем у исходного аустенита Хс=х₀, причем х“<х^«1, а содержание элементов замещения (например, хрома) в у- и a-фазах остается неизменным. Изменение свободной энергии при образовании зародыша феррита в бинарном сплаве Fe-C определяется выражением

AG=x“^-p“)+(l-x“)(^-p“e), (8) где ц - химические потенциалы углерода и железа в у- и a-фазе, которое в [3] было преобразовано к виду

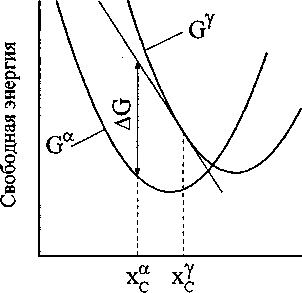
AG = О' (x^-G*(х“)-(х* -Хс )^- (9) Геометрический смысл выражения (9) иллюстрирует рис. 2. Все необходимые термодинамические данные для расчета AG приведены в [10].

Концентрация углерода

Рис. 2. Изменение молярной свободной энергии при зарождении a-фазы, концентрация которой отлична от концентрации у-фазы (схема)

Рассчитанные зависимости свободной энергии зарождения a-фазы от концентрации углерода в а-зародыше имеют максимум, который соответствует очень низкой концентрации углерода. Во многих работах [11, 12] предполагается, что зародыш ос-фазы имеет состав, отвечающий этому максимуму. Тогда bG«bG;;acr-RTx0. (io)

Согласно гипотезе Хиллерта, зарождение а-фазы может произойти, если AG>AGS- Если мы предполагаем, что в основе бейнитного превращения в стали лежит мартенситное превращение в безугле-родистом сплаве [13], то значение AGS должно быть таким же, как и при мартенситном превращении в основе. Верхняя температурная граница образования бейнита Ts определяется условием AG = AGS. Но если начало превращения в стали оценивается по разности свободных энергий у- и сс-фаз безуглеродистого сплава, то (AGFe.Cr) =EGs+RTsx0. Это выражение фактически означает, что верхняя температурная граница бейнитного превращения линейно снижается по мере роста концентрации углерода, что экспериментально показано в [10]. Помимо сомножителя, связанного с энергетическим барьером зарождения, скорость зарождения, по нашему предположению, зависит от скорости роста через вероятность перехода атомов через межфазную границу (6).

Проблема диффузионного роста кристаллов a-фазы из аустенита была рассмотрена Б.Я. Любо-вым [7]. Образование феррита включает перестройку кристаллической решетки, которую формально можно описать как переход атомов железа через межфазную поверхность под влиянием разности химических потенциалов железа в двух фазах, и диффузионный отвод атомов углерода от границы раздела фаз:

dt RT^{X 5е Ре} где р - радиус кривизны растущего кристалла; К_х - коэффициент подвижности межфазной границы, а величина AG_S включает энергию искажений и энергию поверхности раздела.

С другой стороны, по Хиллерту, если скорость роста определяется диффузионным потоком углерода от межфазной границы в глубь аустенита в условиях локального равновесия атомов углерода на самой границе, то

=                                    (12)

8aK_Fe х₀-х^

где Д, = D_oexp(-G_c/7?7’) - коэффициент диффузии углерода в у-фазе; ст - межфазная поверхностная энергия; у^ - парциальный молярный объем железа в сплавах Fe-C.

Выравнивание скоростей роста, определенных соотношениями (11) и (12), происходит, на наш взгляд, благодаря установлению на межфазной границе таких поверхностных концентраций х^^а и x“^h, при которых величина ^p^Y_e-p“_e-AG_s) в уравнении (11) оказывается малой. Мы примем ее равной нулю. Для сильно разбавленных растворов

14 = °14+ЯГ1п(1-ху/“)« “цк-ДГх^;

14 = °ц“_е+ДПп(1-х^)« °ц“_е -RTx^. ⁽¹³⁾ Следовательно, в нашем приближении

YHa _~ rr/a _24z!14z^4 J^?"^ , (14) с с с RT          RT где AGY'a - разность свободных энергий у- и а-фаз чистого железа, которую следует заменить на AGF~aCr для сплава Fe-9 % Сг. Учет AGS приводит к уменьшению х^а по сравнению с равновесным значением; соответственно уменьшается и x“/Y. Если подставить выражение (14) в (12), то в числителе возникнет величина

Знаменатель формулы (12) зависит от разности х₀-х^^н. Когда х₀^х“^/у, скорость роста должна неограниченно возрастать. Однако эксперименты с быстрым охлаждением сплавов Fe-9%Cr [14] свидетельствуют о том, что снижение концентрации углерода от 6,09 до 0,007 % С еще не приводит к резкому увеличению критической скорости охлаждения, определяющейся скоростью роста, то есть для исследуемого сплава х₀» х“^/у.

Тогда с учетом (14)

D_o (AG-AGJ²    ( U_c

—=2—2-----—-ехр -

8стК_Рех₀ RT        ( RT

В сущности, полученная формула отличается от аналогичной формулы для бездиффузионного роста степенью (AG - AGS).

Скорости зарождения (6) равны тогда с учетом поправки Хиллерта:

_r NRD₀ (EG-EGA³ ( Ф+UA , г ₌— нН о -------Д'-exp--^ , (16, а)

МоУВеха (КГ? ( RT )

_r NRD₀ (AG-AGJ³ ( Ф+и-Е} _ 1 =—^-2—5-----д'—exp-----^— - (16,6)

^а &кУ_Еех₀ (RT) I RT )

Обратим внимание на то, что третья степень свободной энергии возникла в выражениях (16) как произведение (AG-AGS)2, входящего в выражение для скорости диффузионного роста (а точнее, вероятности перехода атомов через межфазную границу), и (AG-AGS), входящего в энергетический барьер зарождения. Барьер зарождения при сдвиговых превращениях существенно зависит от плотности дефектов кристаллического строения и упругих напряжений в исходной фазе. Однако движущая сила диффузионного роста, по-видимому, не зависит (или зависит лишь в малой степени) от состояния превращающейся фазы. На это указывает хотя бы тот факт, что образование феррита, в отличие от бейнита и мартенсита, обычно доходит до конца, то есть до/= 1. Поэтому в более общем виде в выражениях (16) следует заменить (AG-AGS)3 на произведение (AG-AGg)E (AG-AG°)3~E, где AGg - термодинамический стимул начала превращения, который, как мы предполагаем, не зависит от количества накопленной фазы, а AGS - тер модинамический стимул зарождения, возрастающий с ростом / так что (AG-AGS) определяется формулой (17). В рассмотренном выше случае 8=1.

В [1] было сделано предположение, что термодинамический стимул AGS возрастает в ходе превращения, так что разность (AG-AGg) уменьшается с ростом степени превращения / и обращается в ноль при / = Уй • Подстановка этого выражения в формулы (6) позволяет найти взаимосвязь/и t; при еп Ф1

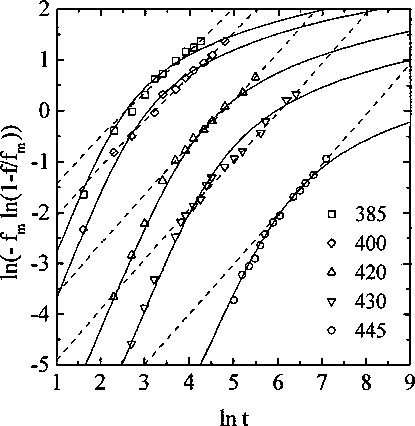
Рис. 3. Сравнение экспериментальных и рассчитанных по уравнениям (18) кинетических кривых образования бейнита. Сплошные линии - при п » 2, пунктирные линии - при л к 1

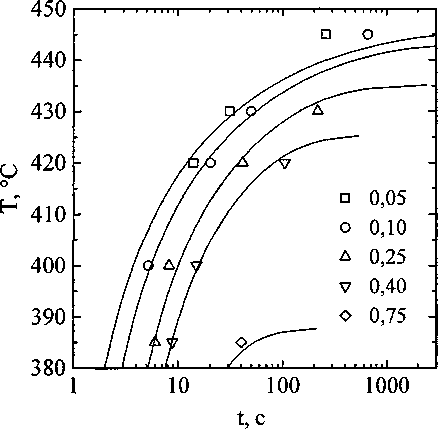
Рис. 4. С-образная диаграмма образования бейнита, рассчитанная по уравнениям (18), в сравнении с экспериментальными данными. Доли превращения указаны на графике

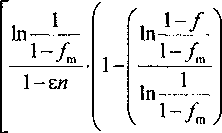
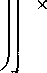
(18, а)

а при еи=1

t = k- ln(l-/_m) ln 1--^х

(rtV

X(ag-ags°)3

•exp

(18,6)

где Q - суммарная энергия активации превращения; k_t - постоянный коэффициент. Формулы (18)

определяют развитие превращения во времени для любой фиксированной температуры.

На рис. 3 рассчитанные по уравнениям (18) кинетические кривые сравниваются с экспериментальными данными (при этом значения п и К были слегка скорректированы для улучшения согласия -см. таблицу).

Интересно, что теоретические кривые при п«2 хорошо согласуются с экспериментом и для тех значений/ для которых мы видели второй участок си»1 на рис. 1, б, то есть эффект уменьшения термодинамического стимула должен приводить к такому же кажущемуся уменьшению п.

Отложив значения 1п(к''" (RTf/(AG-AG°)3) в зависимости от обратной температуры, можно определить по наклону графика энергию актива- ции превращения Q. Найденная таким образом по значениям К из таблицы величина Q составила 85,3 кДж/моль.

Выражения (18) фактически описывают кинетическую диаграмму образования бейнита. На рис. 4 рассчитанная по (18) диаграмма сравнивается с экспериментальной (использованы следующие значения параметров: кр^ЛД⁶ с; е=1; и=2; 2=85,3 кДж/моль). Как видно, их согласие достаточно хорошее.

Таким образом, можно заключить, что подход, который мы предложили ранее для описания кинетики образования пакетного мартенсита, может быть использован и для бейнитного превращения.

Работа поддержана грантом Президента РФ МК-3549.2007.8 и грантом НШ-5965.2006.3.