Кинетика и продолжительность роста усталостных трещин в сталях при переменном нагружении

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2018PNRPU MECHANICS BULLETIN

В инженерной практике актуальной проблемой является проектирование надежных изделий, имеющих обоснованно минимальные запасы прочности, что позволяет значительно снизить металлоемкость изделия, повысить его экономичность и конкурентоспособность. Это является сложной задачей, особенно если компоненты технического объекта испытывают переменные нагрузки. Переменные нагрузки приводят к деградации прочностных характеристик – накоплению усталостных повреждений, возникновению в металле усталостных трещин и в ряде случаев к его разрушению.

Если материал изделия испытывает регулярное циклическое нагружение с постоянными во времени параметрами циклической нагрузки, то долговечность можно оценивать на основании построения кривых выносливости [1], а при исследовании кинетики развития трещин – по кинетической диаграмме усталостного разрушения (КДУР) [2, 3].

Однако если нагружение носит нерегулярный характер, полученный на основе случайных выборок эксплуатационной нагруженности [4–6], то спектр нагружения можно получить в виде временной зависимости на основании тензо-метрирования опасного сечения технического объекта в процессе эксплуатационного нагружения [7] или изучения динамической модели изделия [8]. При этом процесс оценки ресурса усложнится. Имея дело с переменными ампли- тудами нагружения, нужно представлять ту важную роль, которую играет расчет циклов нагружения, по которым рассчитывается долговечность. Такие процедуры производятся на основе зарегистрированных данных нагруженно-сти для моделирования последующей усталости при условии соответствия повреждений элемента при моделировании и оригинальном спектре нагружения. Схематизация спектра нагружения должна помочь извлечь информацию, относящуюся к процессу усталости: метод полных циклов [9] и метод «падающего дождя» (rainflow) [10].

Разнообразие режимов эксплуатации технических объектов предопределяет многообразие моделей случайных процессов, отвечающих эксплуатационной нагружен-ности. Известная взаимосвязь усталости металлов с особенностями внешнего переменного нагружения и окружающей среды ставит перед исследователями задачу тестирования материалов и элементов конструкций с реалистической последовательностью нагрузки. Это дает возможность оценить поведение материала при различных особенностях переменного амплитудного нагружения и определить прочность материалов и конструктивных элементов. Эти цели достигаются использованием стандартных спектров нагружения для различных технических объектов [11–13].

Для снижения стоимости и времени тестирования и моделирования роста трещины могут быть использованы сокращенные варианты реальной истории нагружения [14]. Сокращение истории нагружения включает реальную историю и реальную последовательность нагрузки с отбрасыванием ряда пиковых значений. В этом случае история нагружения может быть приближенно упрощена в виде повторной загрузки блока нагружения с определенной последовательностью нагрузки. В данной работе оценку долговечности по росту трещины проводили с учетом характера случайного нагружения, определенного по выделенному блоку нагружения [15].

Другой подход заключается в суммировании длины трещины на основе каждого отдельного цикла (поцикло-вой расчет) с учетом [16, 17] или без учета взаимодействия амплитуд в последовательности нагрузок [18]. Если рост трещины для данного цикла не зависит от предыстории нагружения и нагрузки носят случайный характер, то в определенном приближении взаимодействием амплитуд можно пренебречь. Однако если в спектре амплитуд наблюдаются высокие перегрузки (недогрузки), то они могут ввести в нагрузку последовательность эффектов, которые существенно повлияют на долговечность роста трещины [19]. В этих случаях модели, включающие эффекты последовательности нагрузок, обеспечивают более точные оценки продолжительности роста трещин [20].

В настоящей работе, на примере четырех марок сталей, проведен анализ кинетики роста усталостных трещин при регулярном и нерегулярном циклическом нагружении с учетом воздействия на процесс роста трещины разной величины асимметрии, амплитуды и характера переменного нагружения. Предложена модель прогнозирования долговечности роста трещины на среднем участке КДУР.

1.    Материал, методика исследования

Испытания на трещиностойкость проводились на сервогидравлической машине BISS Nano-25 [21] на компактных образцах типа С(Т) [22]. Чертёж испытываемого типа образцов представлен на рис. 1. Образцы были изготовлены из стали AISI 4030 (российский аналог – сталь 40ХНМ), стали 9Г2, а также из известных российских марок сталей 40 и 40Х, представленных в нормализованном состоянии. Механические характеристики исследуемых сталей были получены экспериментально при статическом и регулярном симметричном циклическом нагружении. Результаты этих исследований были определены с точностью 5 % и представлены в табл. 1.

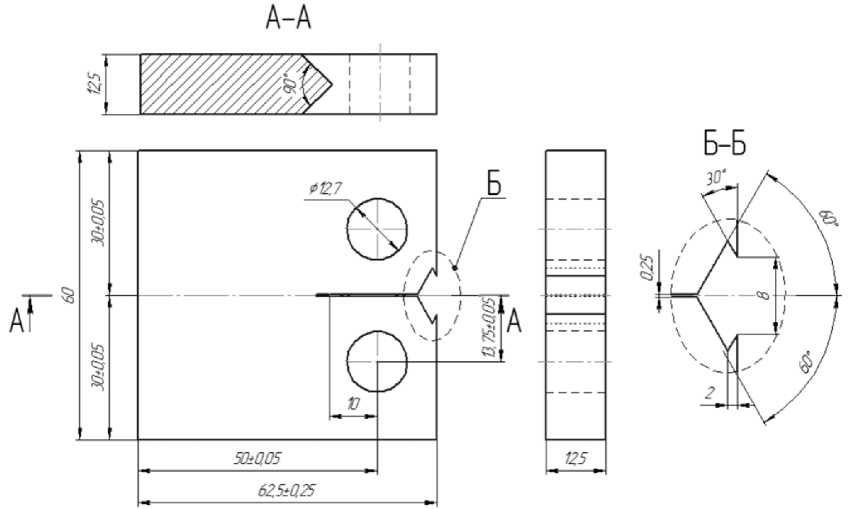
Рис. 1. Геометрия исследуемого образца типа C(T) Fig. 1. Geometry of the studied C(T)-specimen

Механические свойства исследуемых сталей

Таблица 1

Table 1

Mechanical properties of steels under study

Марки сталей	Характеристики прочности
	Предел прочности σ , МПа	Предел текучести σ , МПа	Относительное удлинение δ, %
Сталь AISI 4030	870	690	13
Сталь 40Х	1040	640	10
Сталь 40	580	340	18
Cталь 9Г2	496	303	30

р at max р JP ai max

2000      0                      2000

N, цикл.                             N, цикл.

TV, цикл.

N, цикл.

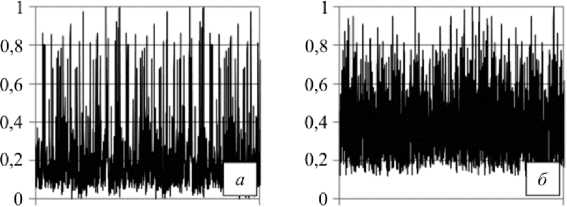
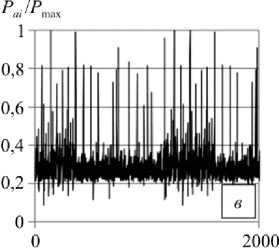
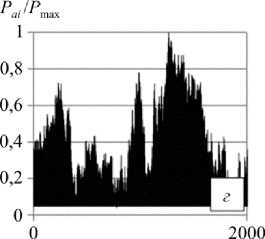
Рис. 2. Выборка из блока случайного нагружения: а – SAETRANS; б – SAEBRACKET; в – SAESUS; г – спектр А; д – спектр С

Fig. 2. Sample of variable amplitude loading block: a – SAETRANS; b – SAEBRACKET; c – SAESUS; d – spectra A; e – spectra C

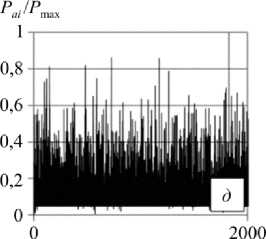
N, цикл.

Экспериментальные исследования проводились с помощью специализированного программного обеспечения MTL-32, осуществляющего управление по нагрузке. C помощью программы VAFCP, позволяющей автоматически обрабатывать результаты испытаний, в процессе испытания записывались все параметры нагружения, и рассчитывалась длина усталостной трещины. Для измерения длины трещины использовался метод податливости [23] с применением датчика раскрытия трещины BISS Bi-06-201, измеряющего расстояние между кромками образца. Испытания проводились на воздухе при нормальных условиях окружающей среды, частота основного вида нагружения – 10 Гц.

2.    Моделирование кинетики и продолжительности роста трещины при регулярном и нерегулярном нагружениях

Исследования на трещиностойкость при регулярном нагружении заключались в проведении испытаний с асимметрией нагрузки R от 0 до 0,5 и величиной максимального нагружения от 3,5 до 15 кН.

Для испытаний при нерегулярном нагружении формировались спектры квазислучайного характера на основании стандартных спектров нагружения, характерных для переменного нагружения различных технических объектов и конструктивных элементов. На рис. 2 показаны примеры нормированных спектров нагружения. Так, спектры МFS (miniFALSTAFF) и MTW (miniTWIST) были сформированы из укороченной вер- сии стандартного спектра нагружения фюзеляжа боевого и транспортного самолета, SАESUS, SAEBRACKET, SAETRANS – укороченные спектры нагружения передней подвески, тормозного механизма и трансмиссии легкового автомобиля [24]. Спектры А и С получены с помощью автокорреляционного подхода [25, 26], основанного на принципе, что величина вектора в двух измерениях, где каждый из компонентов независим, получает случайные переменные по распределению Релея, часто отвечающего различным видам реального случайного нагружения.

Спектры А и С имели одинаковое значение максимальной нагрузки блока нагружения P max равное 15 кН, и асимметрию блоков нагружения R = 0, спектры SAE также имели максимальное значение нагрузки P _max = 15 кН, но различную асимметрию блока нагружения. Для стали AISI 4030 cпектры В и М были получены из спектра А c моделированием различных асимметрий блока R > 0 и разма-хов нагрузки. Спектры В₁–В₃ имели одинаковое значение максимальной нагрузки P max = P a max = 15 кН, но разные значения амплитудной P a и средней P m нагрузки, и различные асимметрии блока нагружения R . Спектры М₁–М₃ имели одинаковую амплитуду нагружения P_a и разные значения P a max , P m и R .

Для сталей 40 и 40X для всех видов спектров нерегулярного нагружения принималось одинаковое значение максимальной нагрузки блока нагружения P max , равное 15 кН, и асимметрия блоков нагружения R = 0,1.

Низколегированная сталь 9Г2 для изучения влияния асимметрии блока нагружения на кинетику роста и дол- говечность трещины при регулярном нагружении испытывалась с одинаковым максимальным значением нагрузки Pmax = Pamax = 5 кН и различной асимметрией блока нагружения. При нерегулярном нагружении различными спектрами изучалось влияние максимальной нагрузки Pmax от 3,5 до 7 кН на продолжительность роста усталостной трещины.

Спектры нагружения предварительно нормализовались по параметру Pai /Pamax и формировались с положи- тельными амплитудами нагрузки (R > 0). Блок нагружения для различных спектров составлял 5000 циклов. Программы исследований по оценке кинетики и продолжительности роста усталостных трещины показаны в табл. 2. Расчётные и экспериментальные значения долговечностей округлялись до целых тысячей циклов.

Отличие нерегулярного нагружения от регулярного оценивается с помощью меры нерегулярности (полноты) V [27]:

Таблица 2

Программа исследований и результаты расчета трещины сталей

Tests schedule and results of crack’s life calculation

Table 2

	Нагружение	Р max , кН	R	V	K	N э, млн цикл.	N val, млн цикл.	N ц, млн цикл.	Номер позиций на рис. 3
	CAL	15	0,1	1	1	0,42	–	0,027	1
	SAETRANS	15	0,1	0,381	20	0,495	0,824	0,711	2
	SAEBRACKET	15	0,1	0,401	18	0,395	0,748	0,59	3
	SAESUS	15	0,1	0,277	32	1,33	1,358	2,143	4
	Спектр М1	16.5	0,455	0,331	25	1,56	1,048	1,151	5
	Спектр М2	15	0,4	0,365	21	1	0,89	0,818	6
	Спектр М3	12	0,25	0,391	19	1,1	0,786	0,644	7
	Спектр В 1	15	0,6	0,243	38	2,5	1,599	3,387	8
	Спектр В 2	15	0,4	0,365	21	1	0,89	0,818	9
	Спектр В3	15	0	0,608	7	0,168	0,277	0,14	10
	Спектр С	15	0,1	0,296	30	1,26	1,24	1,66	11
	Спектр А	15	0,1	0,41	17	0,496	0,717	0,541	12
t а	CAL	5	0	1	1	0,08	–	0,063	1
		5	0,1	1	1	0,062	–	0,073	2
		5	0,3	1	1	0,118	–	0,112	3
		5	0,5	1	1	0,31	–	0,235	4
		5	0,7	1	1	1,09	–	0,911	5
		5	0,75	1	1	1,701	–	1,553	6
	SAETRANS	3.5	0,1	0,381	20	5,3	4,815	7,258	7
		5	0	0,381	20	1,77	1,821	1,733	8
		7	0,1	0,381	20	0,553	0,616	0,627	9
	SAEBRACKET	3.5	0,1	0,401	18	3,404	4,319	6,068	10
		5	0	0,401	18	1,277	1,633	1,45	11
		7	0,1	0,401	18	0,488	0,522	0,525	12
	SAESUS	3,5	0,1	0,277	32	14,317	8,474	6,289	13
		5	0	0,277	32	5,325	3,204	5,281	14
		7	0,1	0,277	32	1,957	1,083	1,907	15
	Спектр А	7	0,1	0,391	19	0,641	0,583	0,573	16
	Спектр С	7	0,1	0,296	30	1,523	0,977	1,512	17
§	CAL	15	0,1	1	1	0,03	–	0,02	1
	SAETRANS	15	0,1	0,381	20	0,464	0,588	0,509	2
	SAEBRACKET	15	0,1	0,401	18	0,375	0,534	0,422	3
	SAESUS	15	0,1	0,277	32	1,51	0,97	1,532	4
	Спектр С	15	0,1	0,296	29	1,19	0,877	1,187	5
t а	CAL	15	0,1	1	1	0,035	–	0,02	1
	SAETRANS	15	0,1	0,381	20	0,475	0,686	0,509	2
	SAEBRACKET	15	0,1	0,401	18	0,334	0,624	0,422	3
	SAESUS	15	0,1	0,277	32	1,493	1,094	1,532	4
	Спектр С	15	0,1	0,296	29	2,794	1,023	1,184	5
	MFS	15	0,1	0,302	29	0,847	1,004	1,129	6
	MTW	15	0,1	0,322	26	0,456	0,912	0,903	7

Примечание: CAL (constant amplitude loading) – регулярное циклическое нагружение; N _э – количество циклов в экспериментальном исследовании; N_VAL – продолжительность роста трещины по предлагаемой модели, N _ц – продолжительность роста трещины по поцикловому методу.

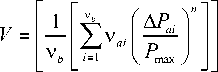
через коэффициент нерегулярности V при одинаковых силовых параметрах P _max и R без учета взаимодействия амплитуд в спектре нагружений [30].

где v_b, v_a - продолжительность используемой выборки и блока переменного нагружения с нагрузкой AP_at ; A p / Р^ - нормированная i -я амплитуда нагружения. Для используемых спектров нагружения принималось v_аi = 1. Для регулярного нагружения значение полноты V принималось равным единице.

Для регулярных и нерегулярных нагружений процесс продвижения усталостных трещин на среднем участке КДУР (режим Пэриса) можно было представить степенной зависимостью [28]

da / dN = CAK n . (2)

В настоящем исследовании для сталей 40, 40Х были получены значения C = 7∙10^–14, а для AISI 4030 и 9Г2 C = 5∙10^–14 при одинаковом n = 3,5 в d a /d N (мм/цикл) и Δ K (МПа мм ).

Для учета явления «закрытия» трещины, имеющего место при асимметриях цикла R менее 0,6–0,7 и снижающего скорость роста трещины за счет уменьшения размаха A K , вводится параметр U [29], описывающий закрытие трещины с асимметрией 0,1 ≤ R ≤ 0,7 и определяемый по формуле

U = 0,55 + 0,33 R + 0,12 R 2 . (3)

В нашем расчете эффективный размах коэффициента интенсивности напряжений в устье трещины при регулярном нагружении

A K эфф =AK ■ U ■ V .               (4)

Здесь учитывается влияние «закрытия» трещин и асимметрии цикла нагружения на скорость роста трещины через коэффициент асимметрии R , а характер переменного нагружения через коэффициент нерегулярности V .

Таким образом, прогнозирование роста трещины при регулярном и нерегулярном нагружении можно проводить поцикловым методом по формуле

N = fa кр---1---da, ц J a0 CAKэфф

где N ц – расчетная продолжительность роста трещин при регулярном и нерегулярном нагружениях поцикловым методом; A K^ - эффективный размах коэффициента интенсивности напряжений, определяемый по уравнению (4); а ₀, a _кр – начальная и критическая длина трещины.

Другой подход для оценки продолжительности роста трещины при переменном нагружении N р. VAR основан на предложении рассматривать кинетику роста трещины на основании ее роста при регулярном нагружении N э. CAL и с учетом характера переменного нагружения

^NVAL = ^N э. CAL ■ ^K , K = 10 ⁽¹⁺ A ¹⁸ n )^^1- V )

где А – нормирующий параметр, равный 2–2,5 для исследуемых сталей; К – коэффициент увеличения продолжительности роста усталостной трещины при случайно циклическом нагружении по сравнению с регулярным циклическим нагружением с теми же силовыми параметрами P _max и R .

3.    Обсуждение результатов исследования

На рис. 3 показаны результаты испытаний сталей при регулярном и нерегулярном нагружениях для исследуемых сталей, а также совмещение кривых КДУР, полученных при регулярном и нерегулярном нагружении с представлением их через эффективный коэффициент интенсивности напряжений Δ K _э фф .

На основании зависимостей кинетики роста трещины a- lg N , полученных с использованием датчика раскрытия трещины, программный комплекс испытательной машины автоматически оценивал скорость роста d a/ d N и размах коэффициента интенсивности напряжений ∆K в устье трещины. Эти результаты позволили построить кинетические диаграммы усталостного разрушения КДУР. Номера позиций на рис. 3 соответствуют номерам в табл. 2. Представленные исходные кривые КДУР получены после испытания и прошли операцию выпрямления. Испытания стали 9Г2 при регулярном нагружении при постоянном значении P _max = 5 кН и различных величин асимметрии блока нагружения R = 0–0,75 (см. табл. 2, поз. 1–6) показали, что все кривые КДУР имеют тенденцию к параллельности в логарифмических координатах (lg(d a /d N )–lg(Δ K )). Но с увеличением асимметрии блока нагружения R они снижаются в сторону меньших скоростей роста трещины и размаха коэффициента интенсивности напряжений Δ К , а следовательно, приводит к увеличению продолжительности ее роста. Это связано с уменьшением размаха интенсивности напряжений Δ К и изменением ее «закрытия» по уравнению (3).

Стали AISI 4030, 40Х, 40 показали, что при одинаковых значениях Р max = 15 кН и асимметриях R = 00,1 при нерегулярном нагружении с различными спектрами нагружения, наряду с «закрытием» трещины по уравнению (3) существенное влияние на кинетику роста трещины оказывает характеристика V – нерегулярность случайного нагружения (1). Особенно видно это по положению исходных КДУР для сталей 40, 40Х, где при уменьшении V в различных спектрах они смещаются вниз, по сравнению КДУР при регулярном нагружении, сохраняя параллельность в этих координатах, что снижает продолжительность роста трещины.

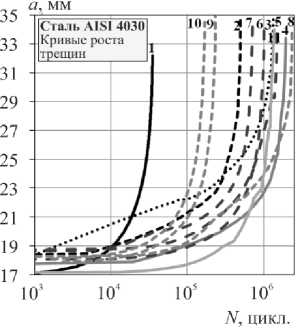
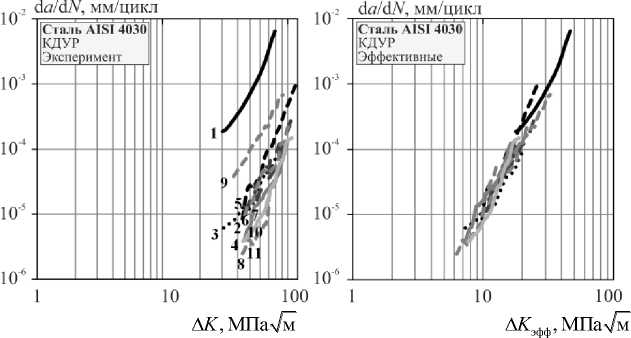
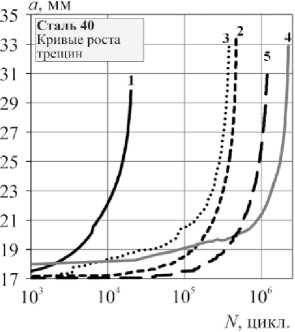
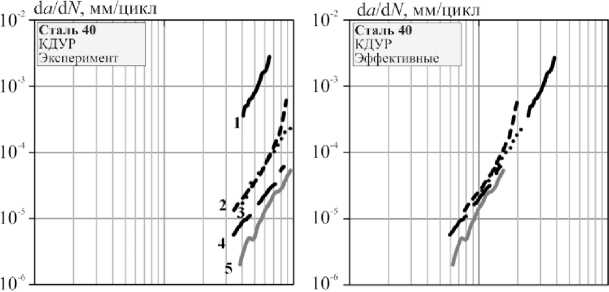
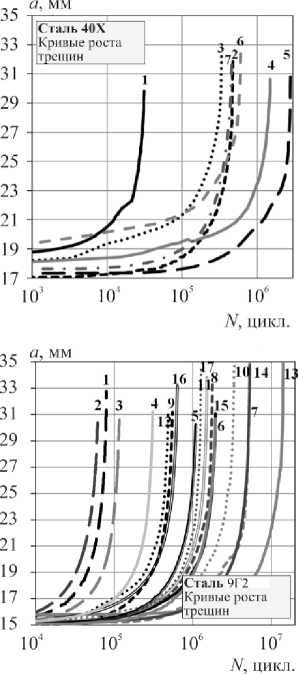
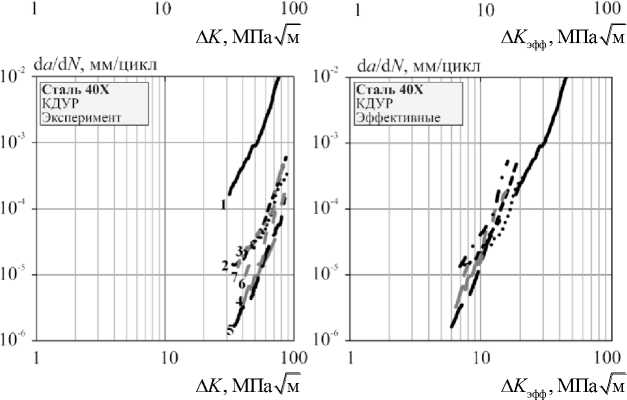
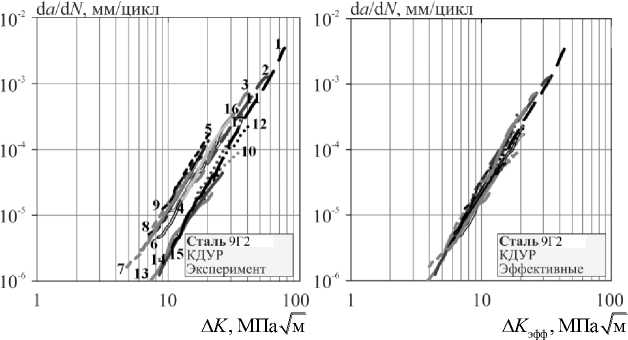
Рис. 3. Кривые роста, экспериментальные и эффективные КДУР испытаний сталей Fig. 3. Fatigue crack growth curves and crack growth rates with the allowance of Δ K_e ff

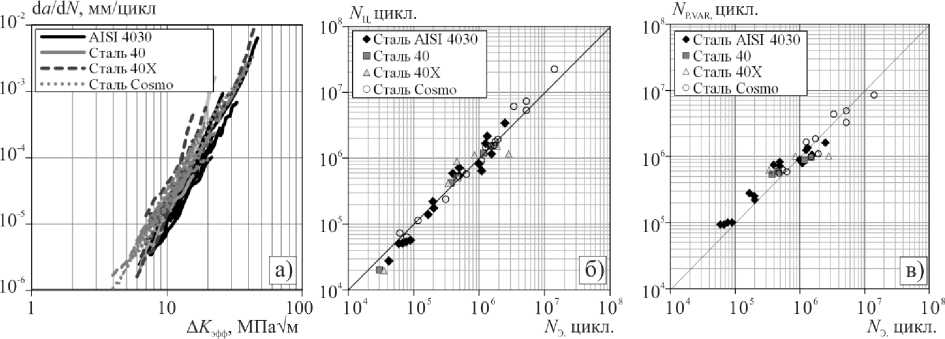
Рис 4. Обобщенные эффективные КДУР для исследуемых сталей ( а ); расчет продолжительности роста трещины поцикловым методом ( б ) и по формуле (6); по сравнению с экспериментом ( в ) Fig. 4. Generalized fatigue crack growth rate curves with the allowance of K_e ff ( а ); calculated crack growth life by "cycle-by-cycle" ( b ) and by formula (6); ( c ) is in comparson with the experimental data

Исследование кинетики стали AISI 4030 при нерегулярном нагружении спектрами В₁–В₃ с постоянным значением Р mах = 15 кН и переменными значениями R (см. табл. 2, поз. 8–10) выявили увеличение долговечности роста трещины от 0,168 до 2,5 млн циклов с увеличением К от 0 до 0,6, а следовательно, с уменьшением размахов Δ К в спектре нагружения. Нерегулярное нагружение спектрами М₁–М₃ с переменным Р _mах от 16,5 до 12 кН с постоянным значением Δ К и уменьшением R от 0,455 до 0,25 (см. табл. 2, поз. 5–7) показало, что такое изменение силовых параметров приводит к снижению долговечности роста трещины и увеличению влияния «закрытия» трещины и коэффициента нерегулярности. Подробный анализ представлен в [28].

Было проведено перестроение кривых КДУР для различных сталей с учетом эффективного коэффициента интенсивностей напряжений К эфф (4), описывающего влияние закрытия трещины U (3) и характера случайного циклического нагружения V (1). Принятый подход показал правильность принятых допущений. Кривые КДУР для исследуемых сталей при регулярном и нерегулярном нагружении различными спектрами и силовыми параметрами стремятся сгруппироваться на одни эквивалентные кривые (см. рис. 3). Была проведена попытка совместной группировки всех исследуемых сталей на одну кривую КДУР на основании введенного значения Δ K эфф.

На рис. 4, а показано совмещение эффективных КДУР для всех исследованных сталей, полученных при регулярном и нерегулярном нагружениях через их представление с эффективным коэффициентом интенсивности напряжений ΔKэфф по формуле (4). Такой подход однозначно может описывать влияние различных силовых параметров и характер нерегулярного нагружения на интенсивность напряжений в устье растущей усталостной трещины. На рис. 4, б представлены сравнительные результаты расчета нерегулярного и регулярного нагружений поцикловым методом Nц по фор- муле (5) и экспериментальных результатов Nэ. На рис. 4 в показана взаимосвязь продолжительности роста трещины нерегулярного нагружения Nр.VAR по формуле (6) от экспериментальной Nэ. Результаты сравнительного расчета и отдельных опытов показаны в табл. 2. Коэффициент корреляции расчета и эксперимента r = 0,96.

Выводы:

• 1.    Показан подход к оценке продолжительности роста усталостной трещины при регулярном и нерегулярном нагружении с различными параметрами силового воздействия, учитывающими «закрытие» трещины и характер случайного нагружения.

• 2.    Проведены испытания компактных образцов при регулярном и нерегулярном циклическом нагружении на трещиностойкость при различных силовых параметрах и разном характере случайного нагружения. Показано, что использование эффективного коэффициента интенсивности напряжений, учитывающего «закрытие» трещины и нерегулярность переменного нагружения, позволяет свести кривые КДУР к эквивалентной кривой.

• 3.    Предложена модель и проведен сравнительный анализ расчета продолжительности роста трещины по предложенному подходу с полученными экспериментальными данными. Соответствие расчета и эксперимента показало перспективность предложенного метода.

Работа выполнена при финансовой поддержке РФФИ (грант № 17-08-01648 А) и гранта Президента РФ МК-943.2017.8.

Acknowledgements

The work was carried out with the financial support of the Russian Foundation for Basic Research (grant Nr. 17-08-01648 А) and the Russian Federation Presidential Grant МК-943.2017.8.